多率量測下隨機跳變系統遷移交互多模型估計

高 爽 欒小麗 趙順毅 劉 飛

由于測量手段的不同,導致量測數據具有不同 的特征,如常規傳感器量測數據與在線分析儀數據相比,雖然采樣速率高,但數據精度較低[1-3];對于飛航導彈而言,高采樣速率的慣導數據短期動態品質好,而雙星定位系統在較長的時間內,可以提供精度較高的位置信息[4].因此,為了獲得更精確的狀態估計值,在立足常規量測值時,如何更好地利用輔助量測數據引起了國內外學者的廣泛關注.其中,融合策略是一種常見的方法,如航跡融合方法[5](Track to track fusion,TTF) 利用相關性對不同濾波器的估計值進行融合,并廣泛應用于信息融合領域.后來,各種延伸的融合估計方法被陸續提出[6].然而,上述融合策略局限于各類傳感器采樣周期一致的情況,當采樣速率不同時,估計策略往往在常規量測的基礎上,利用額外的量測數據對其進行修正.換言之,額外量測值僅僅是錦上添花.鑒于此,學者們提出了不同額外信息利用策略來提升狀態估計效果[7-9].如文獻[10]提出當慢速率數據可獲得時,利用數據融合的方法將不同量測數據下獲得的估計值進行融合.進一步,最優融合策略[11]也被用來處理不同量測數據下卡爾曼濾波器獲得的估計值,針對最優求解困難的問題,文獻[12-13]從智能學習的角度提出了新的優化策略.在此基礎上,文獻[14]考慮到噪聲參數的不確定性,利用修正后的卡爾曼濾波器估計值進行融合,并分析了其收斂性.另一方面,考慮到多率量測信息之間噪聲的相關性,文獻[15]采用矩陣加權的方法,提出了最小方差意義下的分布式融合估計策略.進一步,文獻[16]將噪聲信息從高斯分布推廣到 t 分布以增強估計性能的魯棒性.

除了上述針對單一模態系統在多率量測下的狀態估計,近年來,隨機多模態系統在多率量測下的狀態估計也取得了很大進展.文獻[17]將TTF 融合方法從單一模態系統拓展到跳變系統,然而,其融合權重依賴于協方差矩陣.后來,文獻[18-19]利用一致性理論,在多模型框架下提出了分布式融合策略.文獻[20]則提出了一種基于融合預測的交互多模型算法,通過修改交互多模型算法 (The interacting multiple model,IMM)融合預測來最小化噪聲和低數據率的影響.文獻[21]在高斯混合概率假設的濾波框架下,提出了多級協同的融合方法.針對多個局部無序量測數據,基于最優線性無偏估計,文獻[22]提出了一種具有多個任意階躍滯后的最優集中估計算法.文獻[23]提出了一種連續多速率采樣數據融合方法設計網絡濾波器,解決多傳感器異步采樣難題.另一方面,基于H∞策略的魯棒交互式多模型算法也陸續被提出[24-26],這些文獻采用最優信息融合準則實現不同量測信息下的融合.另外一種可行的思路是借鑒變結構多模型估計思想[27-28],將慢速率量測的估計值作為一種新的模態嵌入到多模型框架中.雖然上述融合策略可以借助于額外信息,從不同角度為多率量測下的狀態估計提供了可能,但其本質是對估計結果的折衷與加權,即額外信息的利用并沒有改變狀態估計器的本質結構,更無法量化慢速率輔助量測信息對估計精度的影響.

因此,本文針對具有多率量測信息的隨機跳變系統,從遷移學習的角度設計一種新的交互多模型估計器.該方法利用源域濾波器處理緩慢、不規則采樣且不易獲得的高精度輔助量測數據,而通過目標域濾波器處理快速、規則采樣和無延遲的常規量測數據.同時,利用平滑策略實現源域慢速率輔助量測信息到目標域快速率數據的知識遷移.然后,通過定義利用常規量測數據獲得的待估計狀態的后驗概率與引入高精度輔助量測數據獲得的待估計狀態的后驗概率之間差異性度量方法,求解最優的貝葉斯遷移估計器,實現輔助信息的充分利用,提高了估計精度.本文的創新點和貢獻主要體現在以下4 個方面:1) 不同于融合策略,在遷移估計器的結構中,嵌入了遷移平滑步,實現輔助量測信息有效利用的同時,解決多率量測下的貝葉斯估計難題;2) 利用平滑策略不僅架起了源域濾波器與目標域濾波器之間知識傳遞的橋梁,也將貝葉斯遷移學習拓展到多率量測下的狀態估計領域;3) 設計的遷移濾波器能同時學習源域和目標域中包含的知識,可以提高估計精度;4) 構建了輔助量測數據與估計性能之間的解析關系,可以定量評價源域數據的引入對估計性能的影響.

1 問題描述

考慮如下馬爾科夫跳變系統,并假設系統可以獲得多種量測數據,以圖1 中的兩種為例.

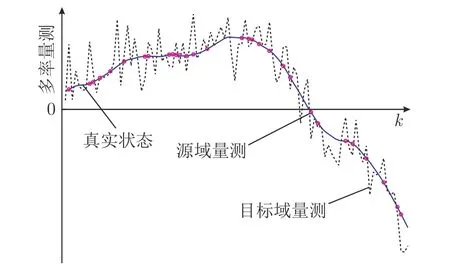
圖1 多率量測過程 (實線表示真實狀態,虛線表示目標域量測 (在線快速率數據),點表示源域量測 (離線化驗數據),其采樣時間可能不規律)Fig.1 Multiple source measurements of the process with different sampling rates (Solid lines are true states,and dashed lines represent target measurements.Dots denote source measurements,whose sample time may be irregular)

本文的任務是在快速率、規則但不精確的量測情況下,輔以慢速率、不規則但更精確的源域數據,設計遷移貝葉斯估計器,對系統 (1)～(3) 的狀態進行估計.假設源域濾波器處理慢速率輔助量測數據,目標域濾波器處理常規快速率量測數據,由于源域數據yS,k比目標域量測數據yk更加精確,故源域噪聲方差RS,k比目標域噪聲方差Rk小.同時,通過遷移估計,將源域濾波器提取的知識遷移到目標貝葉斯濾波器,實現估計精度的提升.

在貝葉斯估計中,后驗概率密度函數 (Probability density function,PDF) 提供了狀態變量的完整描述[29],因此根據系統的量測數據Yk={y0,···,yk},貝葉斯估計的任務是計算后驗概率函數p(xk,rk|Yk). 基于此,本文利用概率分布FS刻畫從源域濾波器遷移的知識,因此,任務轉變成求解給定源域知識下的后驗分布,即

2 遷移估計器的設計

根據貝葉斯公式,條件后驗分布計算如下

其中,∝表示正比符號,本文假設遷移知識的形式為源域濾波器中量測邊緣分布,即約束似然函數為

因此,知識遷移后的后驗分布為

利用KL (Kullback-Leibler) 散度量化引入源域數據的修正分布與貝葉斯后驗分布之間的距離[30-31],即在知識約束的集合內對濾波分布進行優化求解

2.1 遷移平滑策略

從式 (9) 的遷移修正步可以看出,貝葉斯遷移中知識遷移的形式為遷移源域濾波器中量測邊緣分布而非源域量測數據,可用下式計算

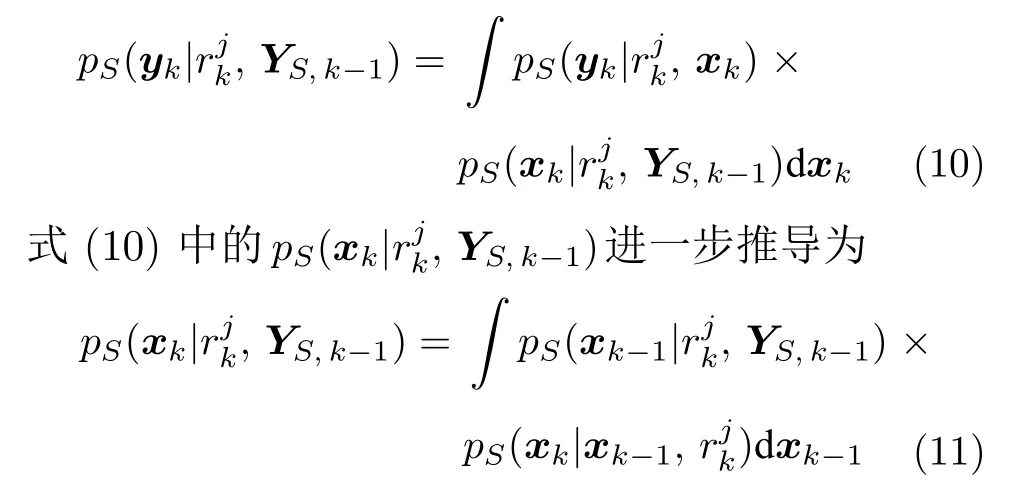
由于慢速率源域量測數據稀疏,式 (11) 中上一時刻的源域濾波器后驗分布難以獲得.且直接利用上一時刻目標域的估計值代替并不能獲得滿意的結果.因此,如何近似求解源域一步滯后估計值是實現遷移的關鍵.本文利用平滑策略結合源域當前時刻可獲得估計值與目標域上一時刻的估計值,即用平滑分布近似代替源域濾波器后驗分布進一步推導可得

注1.不同于傳統處理當前與未來量測值的平滑策略,本文所提平滑策略結合源域與目標域濾波器的估計值,獲取待遷移的估計值.

2.2 遷移交互多模型算法

基于上述分析,面對多率量測信息時,針對馬爾科夫跳變系統,可設計如圖2 所示的遷移估計器結構,混合交互步與IMM 形式一致,即

圖2 遷移交互多模型估計器結構圖Fig.2 Basic operation diagram of the transfer interacting multiple model state estimator

2.3 估計性能評價

為了定量分析源域數據的引入對估計性能的影響,本節利用影響力函數[32-33]來刻畫源域數據遷移對估計性能的影響,量化源域數據的引入對估計精度影響的程度.定義損失函數如下

根據附錄D 提供的推導,源域數據對估計精度的影響力值可由下式計算得到

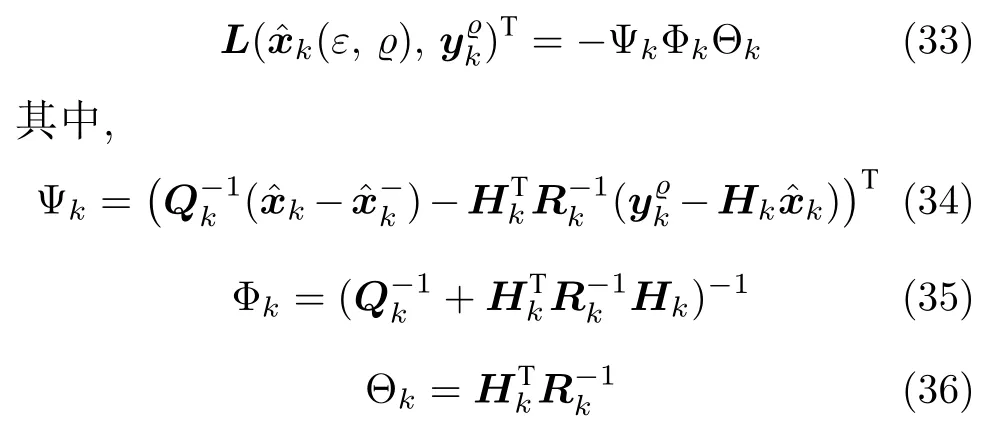
圖3 展示了源域數據的引入對遷移估計器的影響力函數 (Influence function,IF) 曲線和均方根誤差 (Root mean square errors,RMSEs) 曲線,可以看出IF 曲線變化趨勢與RMSEs 趨勢一致,即影響力函數可以有效地用于量化源域數據引入后對估計精度的影響,在對估計性能進行定量分析的同時,也為源域數據質量的評價提供了新的手段,可以有效避免負遷移.

圖3 源域數據對遷移估計器的影響力曲線Fig.3 The influence function of source measurements on the transfer state estimator

3 結果與分析

本節利用運動目標跟蹤例子來說明所提遷移交互多模型估計算法 (Transfer interacting multiple model state estimator,IMM-TF) 的有效性,并與如下3 種方法進行對比:1) 交互多模型算法 (Interacting multiple model,IMM),該算法沒有源域數據遷移,在這里作為基準;2) 交互多模型融合算法(Interacting multiple model fusion,IMM-FU),該算法是多模型下的TTF 常規融合方法;3) 變結構交互多模型算法[34](Variable structure interacting multiple model,VSIMM),該方法把利用源域數據得到的估計值作為新的模態嵌入到IMM 結構中.基于蒙特卡洛采樣計算的RMSEs作為估計性能指標.假設目標的加速度根據有限狀態馬爾科夫鏈演化,動力學方程可描述為

在仿真中,源域量測數據與目標域量測數據的比例為3:5.基于400 次蒙特卡洛仿真,圖4 給出了不同算法下的均方根誤差,可以看出,IMM-TF 估計性能明顯優于IMM、IMM-FU和VSIMM 算法.

圖4 不同算法在運動目標跟蹤中的均方根誤差Fig.4 RMSEs of different algorithms for the moving target tracking

此外,本文分析了源域數據數量和質量對估計性能的影響,表1 展示了估計精度隨著源域數據比重的增加而增加,說明該方法具有正遷移特性.在圖5 中,本文用不同的量測噪聲方差RS刻畫源域數據質量,讓RS從{0.1,1,10,100,1 000}中取值,分別對應5 種情況,圖中以位置估計效果為例,可以看出當RS＜R時,即源域數據質量高于目標域數據質量時,源域數據質量越高,遷移效果越好,當源域數據質量低于目標域數據質量時,遷移效果甚至不如IMM.圖6 進一步展示了利用本文所提的基于影響力值的遷移估計器算法 (Influence function transfer state estimator,IF-TF) 可以有效避免負遷移的產生,當源域數據質量較差時,該算法根據影響力值自動濾除該源域數據,提高算法的魯棒性.

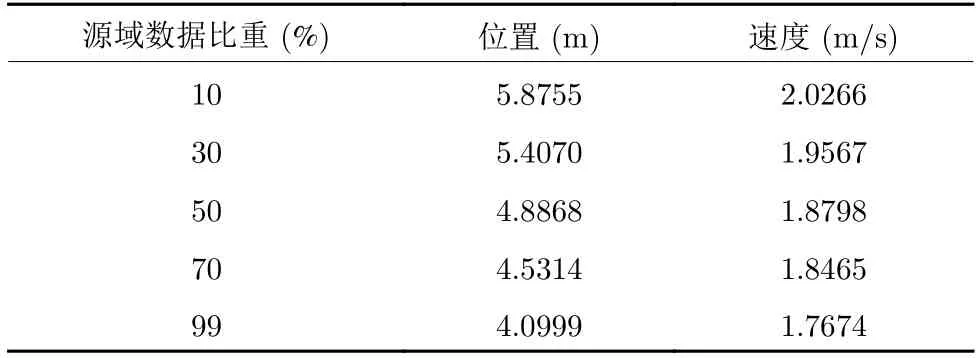
表1 不同數量的源域數據遷移后的 RMSEsTable 1 Average RMSEs (per sample) of IMM-TF in the presence of different amount source measurements

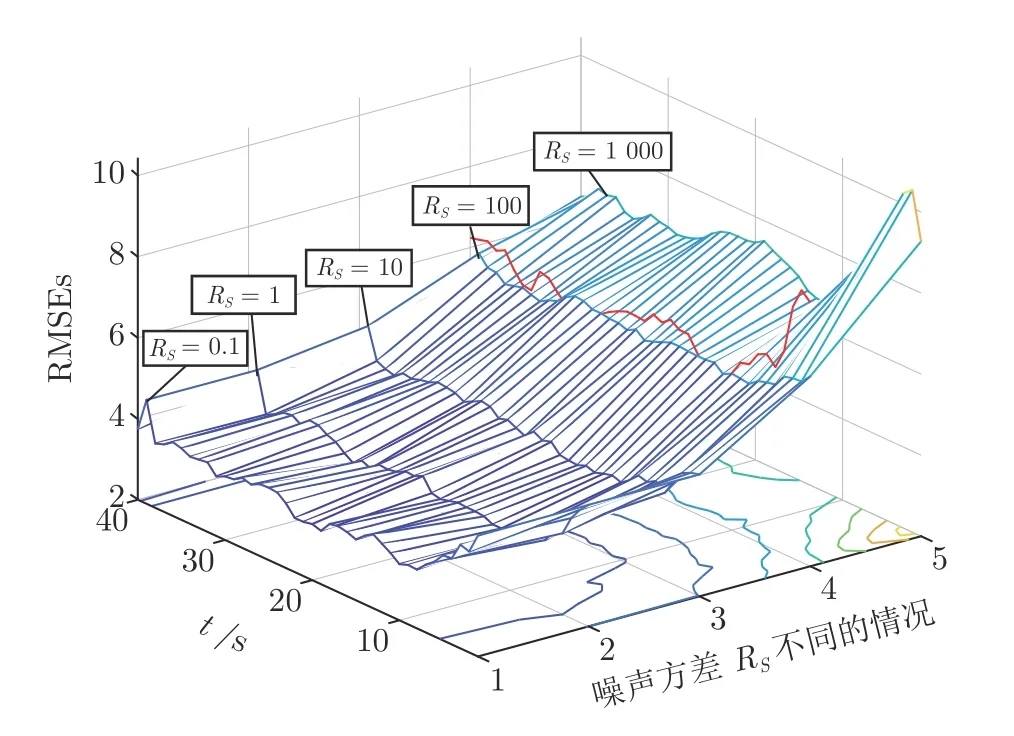
圖5 源域數據質量對遷移估計器算法性能的影響Fig.5 Demonstration of the performance of IMM-TF in the presence of source measurements of different quality

圖6 基于影響力值的遷移估計器算法性能Fig.6 Demonstration of the performance of IF-TF

4 結論

針對多率量測背景下跳變系統的狀態估計問題,本文提出了一種遷移交互多模型估計算法,并利用平滑策略推導了知識遷移的形式,設計了遷移平滑估計器結構,實現了對輔助源域數據的有效利用.同時,通過構建源域量測數據與估計性能之間的解析關系,定量分析了源域量測數據的引入對估計性能的影響.仿真結果表明,本文所提出的遷移估計器IMM-TF 優于VSIMM、IMM和IMM-FU,同時避免了負遷移的產生.由于從源域到目標域的可遷移性和可遷移程度對估計性能起著重要的作用,因此在該框架下如何定義和設計可遷移程度仍然是開放問題.

附錄A.推導式(9)

將式 ( 5)和式 ( 7) 代入式 ( 8) 得到

附錄B.推導式(13)、式(14)

附錄C.推導式(20)～式(23)

附錄D.推導式(33)

根據影響力函數式 (30),進一步推導如下