基于COMSOL Multiphysics的橢圓齒齒板介質的顆粒捕集行為

孫自璽，薛子興，荊子航，盧東方，王毓華，鄭霞裕

(中南大學 資源加工與生物工程學院，湖南 長沙，410083)

高梯度磁選(HGMS)是處理弱磁性物料的有效手段[1]，在生物工程、制藥工程、廢物處理和水處理等許多領域均有應用[2-4]，其中，應用最廣泛的是礦物加工領域。在弱磁性礦物分選中，應用最廣泛的是采用棒介質的立環脈動高梯度磁選機，但采用齒板介質的平環強磁選機在微細粒弱磁性礦物的分選回收方面表現出更優異的效果[5]，被應用于各種弱磁性礦物的分選[6]、鐵尾礦處理[7]及工業除鐵[8]等。

雖然平環強磁選機在細粒弱磁性物料的分選中發揮了巨大作用，但其分選效果仍有待進一步提高，主要存在以下不足之處[9-11]：1) 磁系為水平磁系，漏磁系數較大，背景場強難以進一步提高；2) 采用齒尖角為90°的齒板介質，齒尖易磁化飽和，磁力作用深度較小；3) 齒板介質齒尖易磨損變形，導致分選環境惡化，分選指標不穩定。針對平環強磁選機開展結構優化以提高其分選效果是近年來的研究熱點。磁系和磁介質是高梯度磁選機的兩大核心組成部分，圍繞這兩方面開展結構優化以提高分選效果是可行途徑。平環強磁選機磁系為電磁磁系，其能耗與背景場強的平方成正比[12]，通過增大電流提高磁場強度往往帶來巨大的能耗。因此，近年來強磁選領域的研究重心逐漸由提高磁場強度向提高磁場梯度轉變[13]。而磁場梯度僅與磁介質的特性如形狀、材質和尺寸有關。因此，通過優化磁介質來提高高梯度磁選的效果越來越受到研究人員的重視。

國內外研究人員從材料[14]和形狀[15-16]等方面對磁介質進行了許多研究，但主要集中在棒介質方面，針對齒板介質的研究偏少。有研究表明：軸向配置(平環強磁選機采用的配置方式)下，橢圓形截面棒介質比正方形截面棒介質具有更優異的顆粒捕集性能[17]。而常規齒板介質的單齒類似于半個正方形截面棒介質，兩者的磁場分布具有一定的相似性，且橢圓齒在磁場梯度與磁場深度的均衡性及耐磨損方面都較直角齒有優勢，由此推測橢圓齒齒板介質具有優于常規直角齒齒板介質的顆粒捕集性能。

針對聚磁介質的研究主要包括實測法、數學建模及數值模擬。實測法過程繁瑣，且只能進行定性分析；數學建模僅適用于圓形及橢圓形等較規則的介質類型的顆粒捕集性能研究[18]，齒板介質周圍磁場及流場分布無法通過公式精確地推導計算；數值模擬基于現代計算機仿真技術，可以對不同材料、形狀的棒介質、齒板介質進行顆粒捕集行為的定量研究[19-20]，并給出云圖、等值線圖和顆粒捕集范圍等可視化結果，適用范圍、便捷性及精確度都較數學建模有了巨大的提升，近年來得到了普遍的使用。

本文以常規直角齒齒板介質為基準，在保持介質填充率相同的條件下，通過COMSOL 仿真軟件建立了直角齒齒板介質與一系列橢圓齒齒板介質的仿真模型，研究不同尺寸橢圓齒介質的磁場特性及其對磁性礦物顆粒的捕集性能，并與常規齒板介質進行比較，期望找到一種較適用于平環強磁選機的橢圓齒齒板介質。

1 顆粒運動仿真

1.1 物理模型構建

平環強磁選機屬于軸向配置，高梯度磁選機軸向配置示意圖如圖1所示，齒板介質沿Z軸方向延伸，板面垂直于Y軸。礦漿從Z=0平面以速度v0給入，沿齒板介質延伸方向運動。外加磁場H0均勻分布于磁選空間內，方向垂直于齒板介質板面。

圖1 高梯度磁選機軸向配置示意圖Fig.1 Schematic diagram of axial HGMS

在高梯度磁選機中，礦漿中顆粒所受力除磁力與流體黏性力外還包括范德華力、雙電層力和慣性力等[21-22]，由于不同力的數量級相差很大，研究中通常忽略范德華力、慣性力和雙電層力，僅考慮磁力與流體黏性力對顆粒的作用[23-25]。基于圖1所示坐標系，由于磁力與流體黏性力在Z軸方向均無作用，故在整個分選區間內，給料礦漿沿Z軸以恒速v0運動。由于外加磁場為均勻磁場且齒板介質沿Z軸方向的形狀恒定，故Z軸的任一XY截面上磁力分布均一致，即顆粒在XY平面的運動與Z軸方向的運動互不影響。將顆粒在三維空間中的運動簡化為其在二維平面位置的變化時，顆粒在XY平面的運動情況能準確反映其在整個磁選空間的運動特點。因此，齒板介質周圍顆粒運動的三維問題可簡化為二維問題分析。

基于上述原因，選取XY截面為研究對象，用數值模擬軟件COMSOL 建立了圖2 所示的二維仿真模型，進行磁場分布特性、顆粒運動規律以及顆粒捕集性能的研究。圖2中，流體區域材料設置為水，以恒速v0沿Z軸正向流動。齒板介質處于流體區域的正中心，外加磁場H0沿Y軸負方向均勻分布于整個研究區域。

由于磁介質產生磁力的作用范圍有限，本文重點關注齒板介質外的小范圍區域(圖2 黃色區域外圍長方形區域)。同時，由于齒板介質周圍流場及磁場分布的對稱性，為確保計算準確度的同時降低計算時耗，僅選取虛線所示的均勻流場區域的1/4作為顆粒釋放區域以進行顆粒捕集研究。

圖2 高梯度磁選的2D仿真模型中控制區域的示意圖Fig.2 2D control area in the HGMS simulation models

本文基于常規齒板介質，保持介質充填率(截面積)不變，每個齒的截面積均為4.5 mm2，研究齒板介質橢圓齒設計對弱磁性礦物顆粒的捕集效果。圖3 所示為不同長徑比λ(橢圓齒Y軸與X軸方向軸長之比，即λ=b/a)的橢圓齒齒板介質及常規直角齒齒板介質(簡稱為橢圓齒介質與常規齒板介質)的截面示意圖。模擬參數見表1。齒板介質的軸向長度L=0.1 m，礦漿的運動速度v0=0.1 m/s，故礦漿通過分選空間的時間為1.0 s，因此仿真中僅關注1.0 s內顆粒的運動狀態。

圖3 不同長徑比的橢圓齒介質及直角齒介質截面圖Fig.3 Cross-sections of conventional plates and elliptic tooth plates with different aspect ratios

表1 軸向高梯度磁選機系統的性能參數Table 1 Specifications of axial HGMS system

1.2 顆粒追蹤模型

1.2.1 磁場控制方程

模擬區域內磁場滿足磁通量守恒條件。流體域介質為水，其相對磁導率定義為1，即流體區域磁感應強度B與磁場強度H的關系滿足：

式中：μ為磁導率；μr為相對磁導率；μ0為真空磁導率，為4π×10-7H/m。

聚磁介質的材質為工程純鐵，其B-H曲線如圖4所示，聚磁介質區域的B與H滿足：

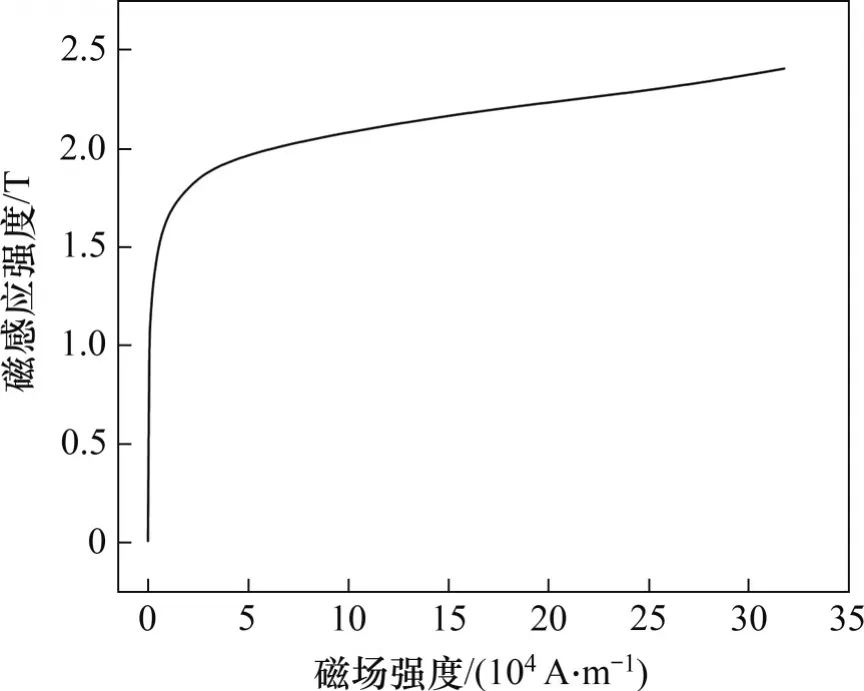
圖4 工程純鐵的B-H曲線Fig.4 B-H curve of Engineering pure iron

如圖3所示，指定二維模型最外側紅色邊界為零標量磁勢Vm=0。因磁場屬于保守場，符合高斯磁通定律：

而高梯度磁選機分選空間內無電流：

由式(3)和式(4)可得磁勢Vm與磁場強度H之間的關系為

1.2.2 流場控制方程

礦漿的初始速度v0=0.1 m/s，沿著磁介質延伸方向做勻速運動。同時礦漿可視為不可壓縮流體，流體滿足Navier-Stokes方程及連續性方程：

式中：ρ為流體密度；P為壓力；v為流體速度；η為流體黏度。

1.2.3 顆粒追蹤

對粒徑為30 μm以下的細粒級顆粒而言，范德華力、雙電層力、慣性力及擴散力等可忽略，僅考慮磁力和流體黏性力的作用，故顆粒的運動滿足下式：

式中：mp為顆粒的質量；vp為顆粒的速度；FD和分別為作用在顆粒上的流體黏性力和磁力，

式中：R為顆粒的半徑。

2 結果與討論

2.1 磁場特性

2.1.1 磁力分布

高梯度磁選機中，顆粒所受磁力與磁場強度和磁場梯度的乘積H·gradH(稱其為磁場力)成正比，故常用H·gradH作為指標對高梯度磁選機的性能做定性評價[26]。通過COMSOL 軟件計算了B0=0.5 T時常規齒板介質和長徑比λ=2的橢圓齒介質周圍的磁場力，結果如圖5所示。由圖5可知，橢圓齒介質與常規齒板介質的磁場力分布相似：齒的上半部分，磁場力指向齒尖，吸引磁性顆粒，齒的下半部分，磁場力背離齒板，排斥磁性顆粒，即兩種介質的齒尖處為磁性吸引區域而齒谷處為磁性排斥區域。

圖5 B0=0.5 T時磁介質周圍歸一化H·gradH矢量分布Fig.5 Normalized H·gradH vector distribution around grooved plate under B0=0.5 T

局部放大的歸一化H·gradH矢量分布如圖6 所示。從圖6可見：當磁感應強度B0=1.5 T時，常規齒板介質與橢圓齒介質的齒尖處仍均為磁性吸引區域，但齒谷處的磁場力分布特性有所不同：常規齒板介質齒谷處仍為磁性排斥區；對于橢圓齒介質，以距離齒谷底部一定距離處為分界面，分界面下方靠近橢圓齒處部分磁場力指向齒板，而齒谷中心線附近的磁場力仍指向上方，即在齒谷底部產生了磁性吸引區域，且對不同長徑比橢圓齒介質的對比發現，隨著長徑比λ的增大，齒谷處磁性吸引區域的面積增大。

圖6 局部放大的歸一化H·gradH矢量分布Fig.6 Partially enlarged view of normalized H·gradH vector distribution around grooved plates

由以上分析可知，在低磁感應強度條件下，常規齒板介質與橢圓齒介質的齒尖附近均為磁性吸引區，齒谷附近均為磁性排斥區。初始位置位于排斥區的磁性顆粒將在斜向齒尖的排斥力的作用下背離齒板向上運動，在運動過程中部分顆粒受磁力作用逐漸向齒尖靠近并最終被齒尖捕集，另一部分顆粒則在磁力與流體黏性力的綜合作用下遠離捕集區域；但隨著磁感應強度的增加(如1.5 T及以上)，常規齒板介質的齒谷區仍為磁性排斥區，橢圓齒介質的齒谷底部將產生局部磁性吸引區域，初始位置位于橢圓齒齒谷底部的磁性顆粒將優先被磁性吸引區域捕集，其余區域的顆粒則在排斥力的作用下向上運動。且由圖6中磁場力云圖可知：B0=1.5 T時，橢圓齒介質的高磁場力區域(圖中深紅色部分)面積比常規齒板介質的大。因此，可以推測，隨著磁感應強度B0的增加及橢圓齒長徑比λ的增大，橢圓齒介質能夠表現出比直角齒介質更優異的顆粒捕集性能。

2.1.2 磁力作用深度

為評估聚磁介質的顆粒捕集性能，以介質周圍高磁場力區域面積表征介質磁力作用深度。圖7所示為磁感應強度B0=0.5 T時齒板介質周圍的磁場力云圖，其中磁場力H·gradH≥1×1014A2/m3的區域顯示為深紅色。由圖7可知，當橢圓齒介質的長徑比λ=0.8 及1.0 時，橢圓齒介質的磁力作用深度比常規齒板介質的小。隨著長徑比λ的增大，橢圓齒介質的磁力作用深度逐漸增加，當λ=3.0時，橢圓齒介質的磁力作用深度已明顯高于常規齒板介質的磁力作用深度。

圖7 B0=0.5 T時磁介質周圍H·gradH云圖Fig.7 Contour plot of H·gradH around grooved plates under B0=0.5 T

為定量比較各條件下齒板介質周圍磁力作用深度，計算了齒板介質周圍磁場力H·gradH≥1×1014A2/m3區域所占的面積，結果見表2。由表2可知，兩類齒板介質的磁力作用深度與磁感應強度成正比，且當磁感應強度一定時，橢圓齒介質的磁力作用深度隨長徑比λ的增大而增加。對比常規齒板介質與橢圓齒介質，當B0=0.1 T時，在所研究的長徑比范圍(λ=0.8～3.0)內，橢圓齒介質的磁力作用深度均比常規齒板介質的小；對于λ=0.8 與1.0的橢圓齒介質，在所研究的磁感應強度范圍(B0=0.1～2.0 T)內其磁力作用深度均比常規齒板介質的小。而當橢圓齒介質長徑比λ=1.5，2.0，3.0 且磁感應強度B0≥0.3 T時，橢圓齒介質的磁力作用深度均比常規齒板介質的大。

表2 H·gradH≥1×1014 A2/m3區域所占的面積Table 2 Surrounded area by isoline of H·gradH≥1×1014 A2/m3 mm2

2.2 顆粒捕集行為分析

2.2.1 顆粒群的運動分析

當t=0 s 時，顆粒釋放區域(Z=0 mm)按密度均勻釋放10 000 顆弱磁性礦物顆粒，顆粒在磁力和流體黏性力的作用下沿不同軌跡運動。以長徑比λ=2.0 的橢圓齒介質為例，繪制了磁感應強度B0=1.5 T、顆粒直徑Dp=15 μm，t=0，0.3，0.7 和1.0 s時顆粒的位置，結果見圖8，圖中，紅色顆粒代表在1.0 s 內被齒板介質捕集的顆粒，綠色顆粒在1.0 s內未能被齒板介質捕集的顆粒，圖8(a)中紅色區域為被捕集顆粒的初始位置，此區域稱為顆粒捕集截面[27]，藍色虛線為顆粒捕集區域的邊界。

圖8 B0=1.5 T,λ=2.0,Dp=15 μm時顆粒捕集截面變化Fig.8 Variation of particle capture cross section for B0=1.5 T, λ=2.0,Dp=15 μm

由圖8可知，位于顆粒釋放區域最外側的顆粒所受磁力較小，在t=0～1.0 s 內其位置基本沒有變化，故顆粒釋放邊界已非有效磁選區域，所選顆粒釋放區域大小是合理的。此外，由紅色顆粒的位置變化可知，顆粒群的運動趨勢與上文磁力的變化相一致：初始位置靠近齒尖的顆粒在磁力作用下向齒尖聚集，初始位置位于齒谷附近的顆粒則在排斥力的作用下遠離齒谷并逐漸向齒尖靠近，其中部分能在1.0 s 內被磁介質捕集。由圖8 還可知，當磁感應強度為1.5 T時，長徑比λ=2.0的橢圓齒介質的顆粒捕集區域為齒尖處與齒谷底部，這與上文所述當磁感應強度B0≥1.5 T時橢圓齒齒谷底部出現磁性吸引區域相一致。

2.2.2 顆粒運動軌跡分析

為了解不同初始位置顆粒的運動軌跡，在B0=1.5 T、λ=2.0、Dp=15 μm 的條件下，選取8 個具有代表性的顆粒，對其軌跡進行追蹤，結果見圖9，其中藍色虛線為顆粒捕集邊界。由圖9可知，初始位置位于顆粒捕集邊界上的顆粒(A1)，在1.0 s 時恰好能被齒板介質捕集；初始位置位于顆粒捕集邊界以外的顆粒(P1，P2)在1.0 s內均未能被齒板介質捕集；初始位置位于顆粒捕集邊界以內的顆粒(A2～A6)在1.0 s內均能被齒板介質捕集。顆粒的運動軌跡有2類，位于齒尖上側及齒谷磁性吸引區域的顆粒持續下降，如P2，A1，A2，A5，A6；位于齒谷磁性排斥區域的顆粒先上升后下降，如P1，A3，A4。這些現象與之前對磁場力分布狀態的分析相符。

圖9 B0=1.5 T,λ=2.0,Dp=15 μm時不同初始位置顆粒的運動軌跡Fig.9 Motion trajectories for 15 μm particles released from the vicinity of plate tooth under magnetic induction B0=1.5 T,λ=2.0,Dp=15 μm

2.3 顆粒捕集截面的變化

2.3.1 直角齒與橢圓齒顆粒捕集截面面積的比較

為直接反應各齒板介質對磁性顆粒的捕集效果，通過COMSOL 軟件導出各時間節點下被釋放顆粒的位置坐標及1.0 s 內最終被捕集顆粒的索引編號，而后通過Matlab 軟件還原并計算不同條件下各類齒板介質的捕集截面面積，其中t=0 s 時不同磁感應強度下齒板介質對直徑5 μm 和10 μm 磁性顆粒的捕集截面面積見圖10。由圖10 可知，在所研究的磁感應強度范圍(0.1～2.0 T)內，高長徑比橢圓齒介質的顆粒捕集截面面積比低長徑比橢圓齒介質的大，且長徑比λ=1.5，2.0，3.0 時，橢圓齒介質的顆粒捕集截面面積比常規齒板介質的大，這表明長徑比λ較大的橢圓齒介質具有優于常規齒板介質的顆粒捕集性能。

圖10 不同聚磁介質顆粒捕集截面面積隨磁感應強度的變化Fig.10 Variation of particle capture cross-section with magnetic induction for plates with different aspect ratios

同時，各齒板介質對不同粒徑顆粒的捕集截面面積隨磁感應強度的變化表現出相同的規律：低磁感應強度下捕集面積隨磁感應強度的增加迅速增加，當磁感應強度較高時，各齒板介質的捕集面積以基本相同的速率緩慢增加。這一規律與聚磁介質的磁化飽和有關：低磁感應強度下各聚磁介質均未達到磁化飽和，聚磁介質周圍磁力隨背景場強的增大迅速增大，直至聚磁介質達到磁化飽和后，聚磁介質周圍磁力的增長速率趨于穩定。圖11所示為齒板介質內部距離頂點0.2 mm處的磁場強度與背景磁感應強度的關系。由圖11 可知：各齒板介質達到磁化飽和的先后順序依次為直角齒、λ=3.0、λ=2.0、λ=1.5、λ=1.0、λ=0.8。除直角齒介質外，該順序與圖10 中各齒板介質顆粒捕集截面面積開始緩慢增加的先后順序相同，其中直角齒介質因尖角易磁化飽和但磁力作用深度淺，其顆粒捕集截面面積的變化與λ=1.5的橢圓齒介質相當。

圖11 磁介質內部距頂點0.2 mm處磁感應強度與磁場強度關系Fig.11 Magnetic induction as a function of magnetic field at 0.2 mm away from vertex of plates from inside

2.3.2 橢圓齒顆粒捕集截面面積隨長徑比的變化

為深入了解橢圓齒介質的顆粒捕集性能，分析橢圓齒介質的顆粒捕集截面面積與顆粒尺寸和長徑比之間的關系，并探求是否存在與棒介質相似的最佳匹配關系[27]。圖12 所示為不同磁感應強度下橢圓齒介質對5 μm 與10 μm 顆粒的捕集截面面積隨長徑比的變化。由圖12 可知：當顆粒尺寸與磁感應強度一定時，橢圓齒介質對磁性顆粒的捕集截面面積變化規律相同：隨著橢圓齒長徑比的增大，顆粒捕集截面面積先增大，而后趨于平緩，當橢圓齒的長徑比超過一定值時，顆粒捕集截面面積的增長基本停滯。且微粒的尺寸越大、磁感應強度越高時，顆粒捕集截面面積增長停滯時所對應的長徑比越大。

圖12 不同磁感應強度下橢圓齒介質顆粒捕集截面面積隨長徑比的變化Fig.12 Variation of particle capture cross-section of elliptical tooth plates with aspect ratio for different magnetic inductions

2.4 展望

本文研究對象為理想狀態下的單塊齒板介質，但在實際應用中，齒板介質往往以交錯排布或相對排布的方式分布于高梯度磁選機中，如圖13 所示。其磁力分布特性因相鄰齒板間的相互影響會有所不同。排布方式、齒距S及齒尖距L等均會對齒板氣隙間的磁力分布產生影響[28-29]。因此，下一步的工作將研究相鄰齒板之間的耦合作用對磁性顆粒捕集行為的影響，并結合實際礦物顆粒捕集試驗，為強磁選機中橢圓齒齒板介質的應用提供更為細致深入的研究數據支撐。

圖13 齒板介質排布示意圖Fig.13 Layout diagram of grooved plates

3 結論

1) 對兩類不同形狀的齒板介質，低場強下齒尖附近均為磁力吸引區域，齒谷附近均為磁力排斥區域，隨著磁感應強度的增大，磁力吸引區域面積增大，磁力排斥區域面積減小。磁場強度或長徑比增大到一定值時，橢圓齒介質齒谷附近也會產生磁力吸引區域。

2) 當橢圓齒介質長徑比λ=1.5，2.0，3.0 且磁感應強度B0≥0.3 T時，橢圓齒介質的磁力作用深度均比常規齒板介質的大。

3) 分選空間中弱磁性顆粒的運動軌跡有兩種：位于磁性吸引區域的顆粒持續下降，并逐漸向齒尖部分靠近；位于磁性排斥區域的顆粒先上升后下降，并有逐漸向齒尖部分靠近的趨勢，其中部分顆粒最終能被齒板介質捕集。

4) 橢圓齒齒板介質的顆粒捕集性能隨長徑比的增大而增大。當λ≥1.5時，橢圓齒齒板介質的顆粒捕集性能優于常規直角齒齒板介質的顆粒捕集性能，即橢圓齒齒板介質在平環強磁選機中具有較大的應用潛力。