繩牽引并聯機構末端執行器運動軌跡精度評價方法

李 航，彭 程，楊 芳，侯澤群，李楊龍

(河南科技大學 機電工程學院，河南 洛陽 471003)

0 引言

運動目標模擬裝置能夠實現特定目標的速度、軌跡等運動狀態模擬，主要用于檢驗跟蹤裝備的跟蹤性能，是裝備從研制到應用過程中一種至關重要的測試設備。目前使用的運動目標模擬裝置[1-2]結構形式多為串聯結構，運動部件慣性較大、工作空間小，只能進行運動目標低速、簡單軌跡的運動狀態模擬，不能進行運動目標高運動狀態(高速、急變速、急轉彎)模擬，適用范圍受到很大限制。

繩牽引并聯機構是一種繼承了剛性并聯機構優點的新型并聯機構，其使用質量輕的繩索代替傳統的剛性支鏈。此類并聯機構主要利用多根繩索來調控末端執行器位姿及運動軌跡，具有工作空間大、運動速度高、慣性小、結構簡單等優點[3-5]，在大型射電望遠鏡饋源支撐系統、飛行器風洞支撐系統、人體康復訓練器、三維打印設備等方面得到應用[6-14]。

近年來，國內外學者在繩牽引并聯機構末端執行器位姿測量方面進行了一些研究工作。文獻[15]提出了一種結合繩索長度測量數據和角位移測量數據的數據融合方法，解決了通過測量繩索長度得到末端執行器位置精度不高的問題，獲得了更為精確的末端執行器位姿。文獻[16]開發了繩牽引并聯機構視覺測量平臺，編寫了一種在線圖像處理程序，對末端執行器的運動位置進行了實時跟蹤，提取了末端執行器位姿數據。文獻[17]提出了一套三維姿態伺服系統，可間接測量出末端執行器的運動姿態。文獻[18]針對用于風洞試驗的多自由度繩牽引并聯機構，用雙目視覺測量系統分別對3種典型運動軌跡下末端執行器動態位姿進行了測量。文獻[19]提出了一種基于彩色編碼的機器視覺位姿測量方法，實現了副油箱風洞模型的位姿動態測量。由于繩牽引并聯機構還沒有在運動目標模擬裝置中應用，故極少見到與運動目標模擬相關的研究文獻。

對于運動目標模擬裝置，其末端執行器的運動軌跡精度直接影響了運動目標模擬的質量。本文針對用于高動態運動目標模擬的平面4繩牽引2自由度并聯機構，基于末端執行器運動軌跡離散點測量數據，研究末端執行器運動軌跡精度評價方法，為提高末端執行器運動軌跡控制精度提供理論依據。

1 軌跡精度評價方法

針對運動目標模擬裝置需要模擬的直線、拋物線和圓運動軌跡，研究基于最小二乘法的軌跡誤差評價方法。

1.1 直線運動軌跡誤差評價方法

基于最小二乘法[20]對直線運動軌跡誤差進行評價，以最小二乘中線為直線運動軌跡的理想直線，與之平行的兩條距離最近且包容實際軌跡線的平行線之間的距離為直線軌跡誤差的最小二乘評價值。計算時以各測量軌跡坐標點偏差值的最小二乘法中線作為評價基線，求得評價基線兩側最遠測量點至該基線的距離，即可求出末端執行器直線運動軌跡的誤差最小二乘法評價值。

按照最小二乘法中線法評價直線軌跡誤差，其誤差值是唯一確定的，具體的步驟如下：

①求解出最小二乘法中線。設工作平面為XOY，平面內的直線方程可表示為：

y=kx+b，

(1)

其中：k、b分別為直線的斜率和在Y軸上的截距。

軌跡上各測量點為Pi(xi,yi)，i=1,2,…，n，由最小二乘法原理，得到目標函數為：

(2)

然后，根據極值原理，要使式(2)的目標函數最小，即：

(3)

聯合式(2)和式(3)可得矩陣方程：

(4)

由式(4)可得最小二乘法中線斜率k和截距b，所以，最小二乘法中線方程為：

(5)

②求各測量點Pi到最小二乘法中線的距離hi，如式(6)所示，然后分別找出兩側測量點至該中線距離的最大值hr-max和hl-max，進而求得末端執行器直線運動軌跡的誤差值δl，

(6)

式(6)為點到直線的距離公式，本文不對其取絕對值，主要原因為：在該公式中當點位于直線的左側時得到的hi為負值，點位于直線的右側時得到的hi為正值，所有負值中的最小值即hl-max，所有正值中的最大值即hr-max，這樣可以很方便地獲得直線兩側最遠點到直線的距離。

δl=hr-max+|hl-max|。

(7)

1.2 拋物線運動軌跡誤差評價方法

基于最小二乘法對拋物線運動軌跡誤差進行評價，首先使用最小二乘法擬合得到最小二乘法拋物線，然后計算出各實際測量點到最小二乘法拋物線的最小法向距離，得到外側測量點到最小二乘法拋物線的最小法向距離中的最大值和內側測量點的最小法向距離中的最小值，最后求出平面內拋物線運動軌跡的誤差值。本文中定義最小法向距離為測量點與該點的拋物線法線與拋物線的最近交點的距離。軌跡誤差評價流程如下：

①擬合出最小二乘拋物線。設平面內的拋物線方程為：

f(x,y)=Ax2+Bx+C-y。

(8)

拋物線運動軌跡上各測量點為Pi(xi,yi)，i=1,2,…，n，根據最小二乘法原理得到目標函數為：

(9)

根據極值原理，要使式(9)的目標函數最小，有：

(10)

聯合式(9)和式(10)可得矩陣方程為：

(11)

對式(11)進一步求解，可得最小二乘拋物線的A、B、C值，即可得最小二乘拋物線方程。

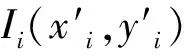
圖1 軌跡測量點與最小二乘拋物線關系圖

(12)

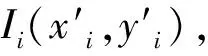
(13)

③判斷各測量點在最小二乘拋物線的方位。根據拋物線的幾何知識，通過計算測量點在最小二乘拋物線方程中值的大小，可以判斷出各個測量點是位于拋物線的外側還是內側。將各測量點分別代入式(8)，當f(x,y)>0時，表明測量點是位于最小二乘拋物線的外側，此時di為正值；當f(x,y)<0時，表明測量點是位于最小二乘拋物線的內側，此時di為負值。

④計算拋物線運動軌跡誤差。將拋物線運動軌跡誤差δp定義為外側各測量點到最小二乘拋物線的最小法向距離中的最大值dmax與內側各測量點的最小法向距離中的最小值dmin之間的差值，即：

δp=dmax-dmin。

(14)

1.3 圓運動軌跡誤差評價方法

基于最小二乘法對圓運動軌跡誤差進行評價，以最小二乘圓作為評價基準，求各測量點到最小二乘圓圓心距離的最大值和最小值，即可求出圓運動軌跡的誤差值。如圖2所示，坐標原點為O，設最小二乘圓的圓心為O′點，在坐標系Oxy中的坐標為(a,b)，最小二乘圓的半徑為R0。圓的軌跡方程可以表示為：

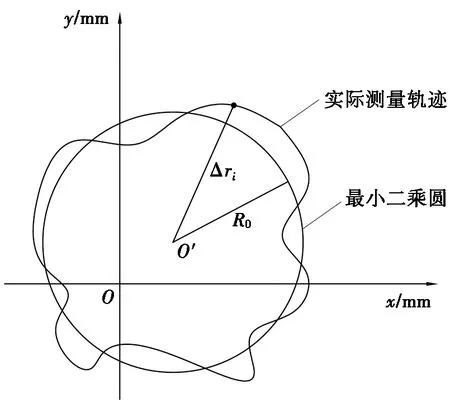
圖2 最小二乘圓法

(15)

圓運動軌跡上各測量點為Pi(xi,yi)，i=1,2,…,n，根據最小二乘原理得到目標函數為：

(16)

為了得到最小化問題的直接解，并且避免平方根，對式(16)進行改進，即：

(17)

進一步可化為：

(18)

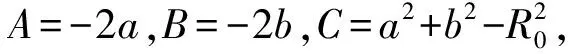
(19)

要使目標函數最小，即：

(20)

聯立式(19)和式(20)可求得A、B、C，然后，根據式(21)可以求出最小二乘圓的圓心坐標和半徑值，即：

(21)

定義各測量點到最小二乘圓圓心的距離Δri為：

(22)

圓運動軌跡誤差δc為Δri中的最大值Δrmax和最小值Δrmin的差值，即：

δc=Δrmax-Δrmin。

(23)

2 試驗及結果分析

2.1 末端執行器運動軌跡點測量方法

圖3為繩牽引并聯機構和末端執行器運動軌跡機器視覺測量系統。利用基于高速攝像機的視覺測量系統對末端執行器的運動圖像進行采集和處理，獲取末端執行器的運動軌跡離散點的二維坐標值。

圖3 繩牽引并聯機構和末端執行器運動軌跡測量系統

相關參數設置：運動圖像分辨率為1 600 pixel×1 086 pixel，采集幀率為30幀/s，直線、拋物線、圓運動軌跡圖像各采集3組。

2.2 運動軌跡測量數據分析和評價

末端執行器運動軌跡方程分別為：

直線運動軌跡方程：

y=x,x∈[-283,283]。

(24)

拋物線運動軌跡方程：

y=0.007 2x2-300,x∈[-283,283]。

(25)

圓運動軌跡方程：

x2+y2=4002,x∈[-400,400]。

(26)

對末端執行器運動軌跡離散點進行擬合，可得到末端執行器的實際運動軌跡，如圖4、圖5和圖6所示。

利用第1節提出的末端執行器軌跡精度評價方法，分別對圖4、圖5和圖6中測量軌跡所表示的數據計算其軌跡誤差。表1、表2和表3分別展示了3種軌跡測量數據的相關計算結果。

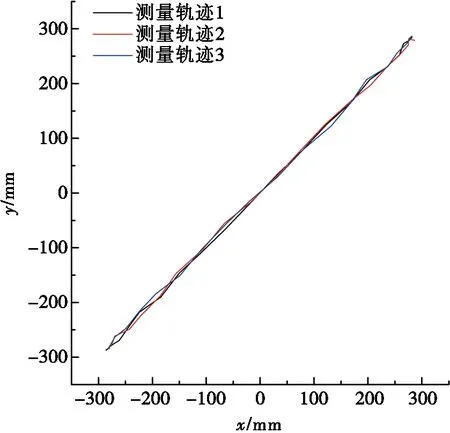
圖4 直線運動測量軌跡

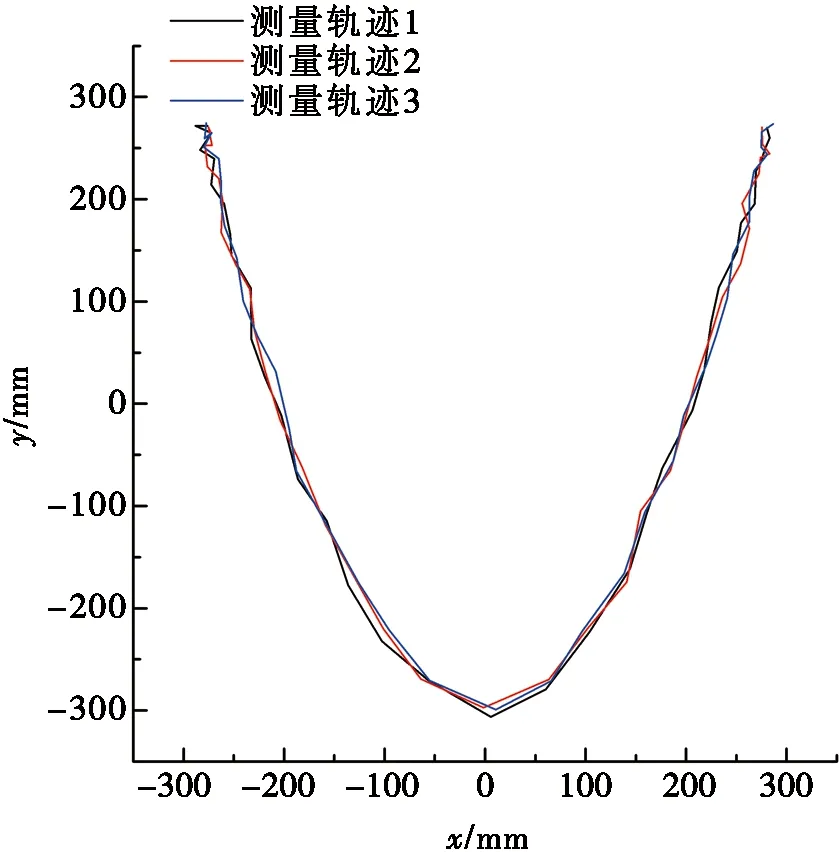
圖5 拋物線運動測量軌跡

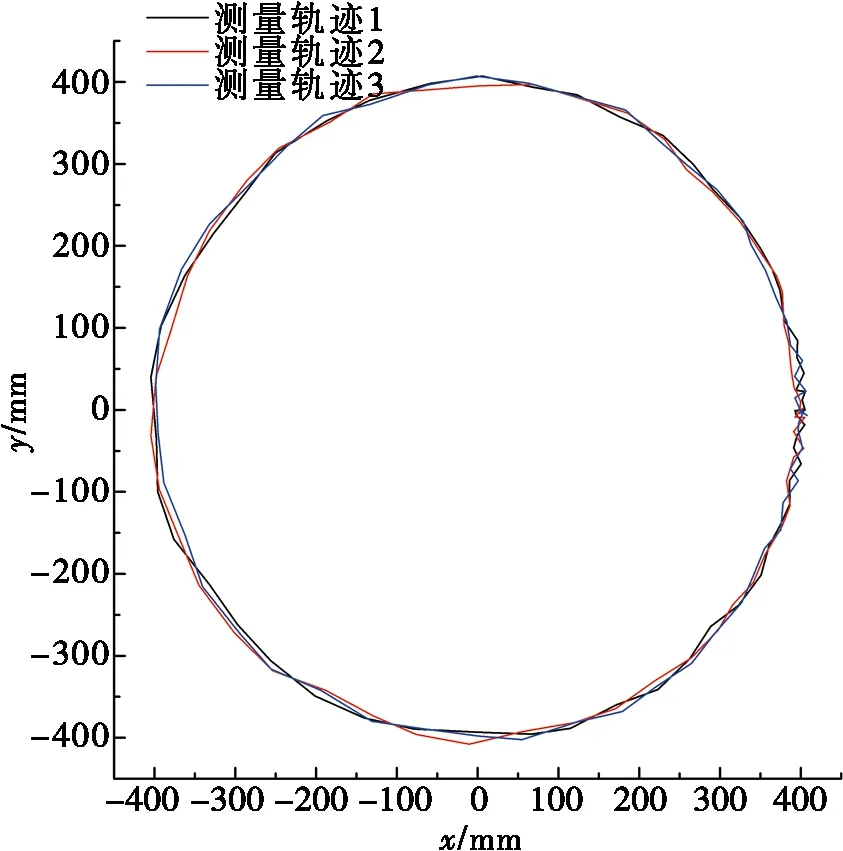
圖6 圓運動測量軌跡

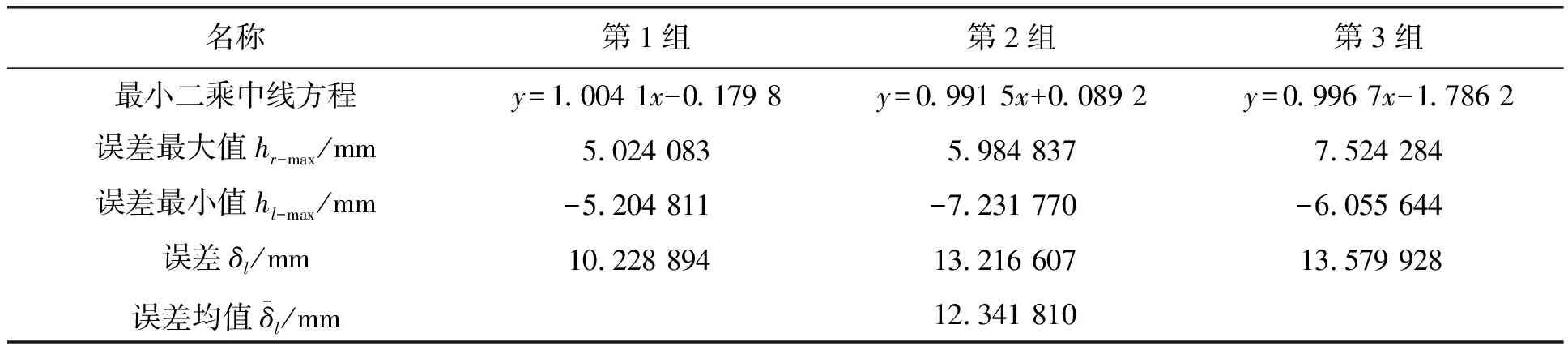
表1 直線運動軌跡誤差計算結果

表2 拋物線運動軌跡誤差計算結果

表3 圓運動軌跡誤差計算結果

由表1～表3中的計算結果可知：直線、拋物線、圓3種運動軌跡的最大誤差絕對數值分別為12.341 810 mm、16.428 087 mm、18.063 675 mm。為更好評判得到的誤差能否滿足裝置的運行精度要求，在測量范圍內對最大誤差絕對數值進行進一步計算。

①直線運動軌跡誤差：

(27)

其中：L為直線運動軌跡長度。

②拋物線運動軌跡誤差：

(28)

其中：Lp為拋物線運動軌跡長度。

③圓運動軌跡誤差：

(29)

其中：D為圓運動軌跡直徑。

2.3 結果分析

由上述計算結果可以看出：分別對3種運動軌跡的測量數據進行計算，得到末端執行器直線運動軌跡誤差為1.54%，拋物線運動軌跡誤差為1.23%，圓運動軌跡誤差為2.26%，圓運動軌跡誤差大于直線運動軌跡誤差，直線運動軌跡誤差大于拋物線運動軌跡誤差。

對軌跡誤差產生的原因進行分析，主要原因有4個：

(Ⅰ)繩牽引并聯機構試驗樣機的制造和安裝誤差。試驗樣機在研制時零部件的加工制造誤差以及安裝定位誤差將直接影響到末端執行器的運動軌跡精度。

(Ⅱ)繩索彈性形變造成的誤差。在末端執行器運動過程中，由于繩索受拉力會有彈性形變，導致繩索實際長度與理論計算長度之間存在偏差，從而使末端執行器實際運動位置與理論運動位置之間存在誤差。

(Ⅲ)控制系統的控制誤差。由于控制系統本身的制造誤差再加上存在外界擾動使得期望輸出量與實際輸出量存在偏差，從而使運動軌跡產生了一定的誤差。

(Ⅳ)測量系統的測量誤差。由于測量系統中單目攝像機存在標定誤差以及環境亮度等對測量系統的影響，導致測量值與真實值之間存在誤差。

3 結束語

本文采用基于機器視覺的測量系統對繩牽引并聯機構末端執行器直線、拋物線和圓運動軌跡進行了測量，基于最小二乘法對測量得到的運動軌跡離散點數據進行了計算，得到了3種運動軌跡的誤差值，完成了末端執行器的軌跡精度評價，為提高末端執行器運動軌跡控制精度提供了理論依據。