基于壓縮感知的波束選擇算法研究

肖利強，劉一凡

(河南科技大學 a.金屬材料磨損控制與成型技術國家地方聯合工程研究中心；b.信息工程學院，河南 洛陽 471023)

0 引言

波束成形可在干擾和噪聲共存情況下以空間選擇性的方式實現信號的發送、接收和轉發。大規模多輸入多輸出(massive multiple input multiple output，Massive MIMO)系統是提高毫米波無線信道頻譜資源利用效率的關鍵技術之一，也是目前第五代移動通信系統(5th generation mobile communication technology，5G)的必備技術[1]。為了能充分發揮Massive MIMO系統大規模天線陣列潛力，勢必搭配波束成形技術。

目前主流的波束成形方法為數字-模擬混合波束成形(hybrid beamforming，HBF)。HBF架構中的整體波束成形器由低維數字波束成形器組成，然后再使用模擬移相器實現射頻波束成形[2-3]。這種架構可使用較少的射頻鏈獲得接近全數字方案的性能。

如果信道狀態信息(channel state information，CSI)在配備天線陣列的基站端(base station, BS)處可用，則可以采用多用戶下行鏈路波束成形來降低多用戶干擾以提高頻譜效率[4]。但是對于毫米波無線通信系統的Massive MIMO來講，從用戶到基站的全CSI反饋會帶來過高的反饋開銷[5]。這種情況下，可以采用有限CSI反饋的下行鏈路波束成形，利用豐富散射環境下的隨機(正交)波束配合用戶選擇算法[6]。

在基于波束選擇的混合波束成形系統中，信號在射頻前端進行空間處理，從而可以減少射頻鏈(radio frequency chain，RF chain)的數量，以節省硬件成本、功耗和導頻開銷[7]。現有的大多數研究都集中在如何設計模擬波束以接近全數字系統的性能，由于波束與用戶密切相關，因此應同時對用戶調度以及波束的選擇進行考慮[8]。文獻[9]考慮到多用戶干擾，將用戶分為干擾組和非干擾組，針對干擾用戶和非干擾用戶分別選擇合適的波束以降低系統復雜度。文獻[10]將波束空間與MIMO相結合，提出了信干噪比(signal to interference plus noise ratio, SINR)最大化與系統容量最大化的波束選擇方案。

在時分雙工(time division duplex, TDD)系統中，存在多組正交波束和多個時隙。每個時隙中，基站使用對應的一組正交波束來發送導頻或訓練信號，并且每個用戶可以選擇正交波束之一，通過反饋其索引用于下行鏈路波束選擇。盡管由于每組正交波束的數量有限，但通過用戶分集，可以實現更好的系統性能[11]。隨著正交波束或時隙組數量的增加，可以提高系統誤碼率、中斷概率等測度性能，但是也會增加訓練開銷。文獻[12]在假設知曉全信道狀態信息的情況下，提出了一種空間重疊索引的概念來處理與其他用戶共享波束造成的干擾以提高系統性能。文獻[13]引入壓縮感知(compressive sensing，CS)，從大尺度空間觀測值來估計稀疏信號或參數。壓縮感知技術還應用于各種稀疏多徑信道估計問題和CSI反饋[14]。例如對于在一定稀疏性(或有限散射)環境下的毫米波信道估計[15]。

本文研究了基于壓縮感知的波束選擇算法，該方法無需使用顯式信道估計，通過引入壓縮感知技術從大尺度空間觀測值估計稀疏信號或參數。仿真分析驗證了該方法在毫米波信道下的性能。

1 系統模型

本文研究基于壓縮感知的波束選擇算法的性能，在構建損耗模型時采用確定性建模方法。確定無線信道的傳播環境為3GPP TR 38.901 V16.1.0中標準的RMa-LOS環境，基站和用戶的天線類型均設置為均勻矩形天線陣列，依據TR 38.901 V16.1.0標準計算模型通用參數，路徑損耗及相關的大尺度參數，根據陣列天線的面板數、天線元件數、元件間距以及極化類型生成天線陣列響應，計算小尺度參數包括時延、簇功率、到達角、離開角、交叉極化功率，根據生成的信道參數以及天線陣列響應，生成隨即初始相位，計算相關系數，添加路徑損耗與陰影衰落，生成信道傳輸矩陣。信道模型的實現過程如圖1所示。

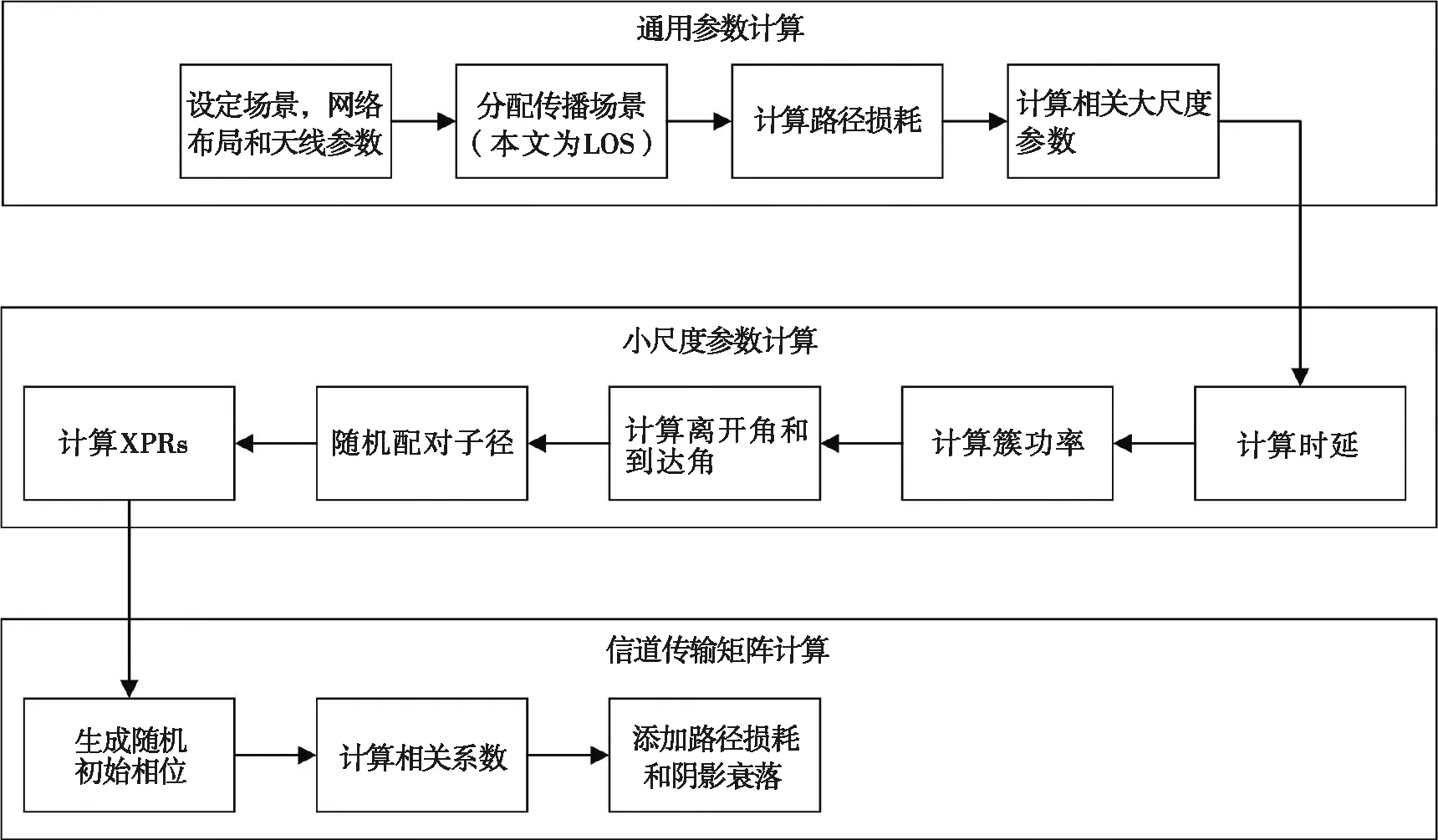
圖1 信道模型的實現過程

為研究不同波束選擇方法的性能，以基站的下行發射總功率以及系統的“和速率”作為標準來衡量系統的性能。以下的建模步驟對下行鏈路進行了仿真，時分雙工系統信道對稱性極強，對上行鏈路進行仿真時，互換到達角與離開角即可。

本文假設每個相干時隙中用戶使用選定的一組波束連接到基站。基于時分雙工的系統，每個時隙分為3個階段。第一階段是通過波束選擇在基站和用戶之間建立連接。第二階段和第三階段分別用于下行鏈路和上行鏈路傳輸。本文僅關注第一個波束選擇階段，該階段可分為4個子階段S1～S4，如圖2所示：

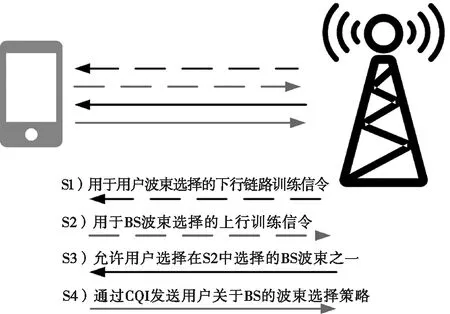
圖2 TDD系統下的波束選擇數據交互過程

前兩個子階段用于發送導頻和訓練信號：第一個子階段由基站向移動用戶發送下行鏈路訓練信令，第二個子階段由移動用戶向基站發送上行訓練信令。后兩個子階段用于波束選擇：第三個子階段由基站向用戶發送允許用戶選擇的波束組，第四個子階段由用戶依據信道質量指示(channel quality indicator，CQI)選擇被分配的波束。

2 基于壓縮感知的波束選擇

本節重點研究基站波束選擇的第二子階段(S2)，無需顯式信道估計即可為用戶選擇合適的波束。如果基站向用戶發送由b表示的訓練信號，則用戶k的接收信號為[16]：

(1)

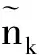
假設基站處為基于TDD的MIMO系統，基站服務的用戶數量為K。

在用戶路徑角度分離條件下，復合通道矢量為[16]：

(2)

其中：P為子徑的數量；hk,p為第k個用戶的第p條路徑的信道系數；aB為BS處天線陣列相應向量；θk,p為BS處的路徑的角度；aU為用戶處天線陣列響應向量；ψk,p為用戶處的路徑角度；uk為用戶k處用于上行鏈路傳輸的波束成形矢量，則用戶k的接收信號為：

(3)

其中:sk=hk,p(k)Tk，Tk為來自用戶k的訓練信號，使：

W=[w(1),…,w(M(B))],

(4)

假設向量W的維度MB足夠大，則每個aB(θk,p(k))可以看為W的近似列向量之一。然后，接收信號可以近似表達為：

r≈Ws+n。

(5)

W可以視為大小LB×MB的測量矩陣，s是大小為MB×1的K維稀疏信號矢量,且MB≥LB≥K[17],因此，可以使用壓縮感知的方法從式(5)接收信號r中估計K維稀疏信號s。

本文采用式(6)來估計稀疏信號s：

(6)

其中:ε由噪聲矢量n決定，式(6)為凸優化問題，理論上可得到全局最優解，但要以計算復雜度為代價。已有各種低復雜度方法如貪婪算法等以尋求近似解。由于用戶設備的計算能力有限，低復雜度求解算法對于用戶波束選擇尤為重要。本文采用正交匹配追蹤算法(orthogonal matching pursuit，OMP)[18-19]用于估計稀疏信號。OMP算法可用已知的測量矩陣W從公式(5)中估計r中的K維稀疏信號s。

基于壓縮感知估計信號s的方法的性能取決于測量矩陣W的相干性和受限等距屬性(restricted isometry property，RIP)。如果，測量矩陣W滿足K階的RIP，即對于所有K維稀疏向量有：

(1-kK)‖s‖2≤‖Ws‖2≤(1+kK)‖s‖2,

(7)

其中:kK∈(0,1)為等距常數。為使用OMP算法恢復K稀疏信號，k2K(或k3K)必須足夠小。由于測量矩陣W的相鄰列向量與MB高度相關，因此需要滿足路徑角分離條件，否則無法獲得較好的預期性能。由基站路徑角分離條件，得{θ1,p(1), … ,θK,p(K)}中任意兩者間的距離，大于或等于maxm|Θm|，即：

(8)

假設基站處路徑角度分離條件成立，則等距常數為：

kK=(K-1)δB,

(9)

如果(K-1)δB足夠小，可以認定W在基站路徑角分離條件下滿足RIP，可以通過基于壓縮感知的方法來估計K維稀疏信號s。

當采用基于壓縮感知的方法在S2中選擇波束時，由于基站是在不與任何特定用戶相關聯的情況下選擇波束，訓練信令不必正交，訓練信令的長度可以縮短為一個字符以減少訓練開銷，在限制系統相干時間方面至關重要。

在用于用戶處波束選擇的S1中，式(1)中xk可近似表示。為了方便起見，本文省略了用戶索引k。令：

U=[u(1), … ,u(Mu)]。

(10)

當Mu足夠大時，公式(1)中的x可以近似為：

(11)

其中:q是p維稀疏向量。可以直接得出用戶路徑角度分離條件下的等距常數，采用式(9)對稀疏信號q進行估計，即(P-1)δU。

可以使用CS的概念分別對公式(5)和公式(11)中的s和q進行估計，因為s和q都很稀疏[5]。如果估計了稀疏的s和q，則對應于s和q的非零元素的波束可以分別用于基站和用戶波束。因此，該方法可以看作沒有直接信道估計的波束選擇。可將基站端的波束選擇過程總結如下：

表1 波束選擇過程

3 實驗驗證

(12)

假設分別在Θ和Ψ上獨立且均勻地生成θk,p和ψk,p，且上行鏈路與下行鏈路的信噪比(singal to noise ratio,SNR)相同。為了進行比較，本節對比了具有SINR約束的多用戶數字波束成形，其目標SINR與CS中的波束選擇系統的目標SINR相同[20]。因此，多用戶數字波束成形的總速率與波束選擇系統的總速率相同。多用戶數字波束成形采用功率控制，在波束選擇仿真中采用相同的功率。

圖3展示了在SNR分別為10 dB和20 dB下整個波束選擇系統面對不同用戶數量時的性能。如圖3所示，系統的總傳輸速率隨用戶數K增加而增加。當K較小時，系統總傳輸速率隨K線性增長。K較大時，增長變得緩慢。因此，系統總傳輸速率關于K近似成對數增長。隨著用戶數目的增加，波束在用戶內距離減小，多用戶干擾會增強，系統總速率的上限會受到多用戶干擾的限制。

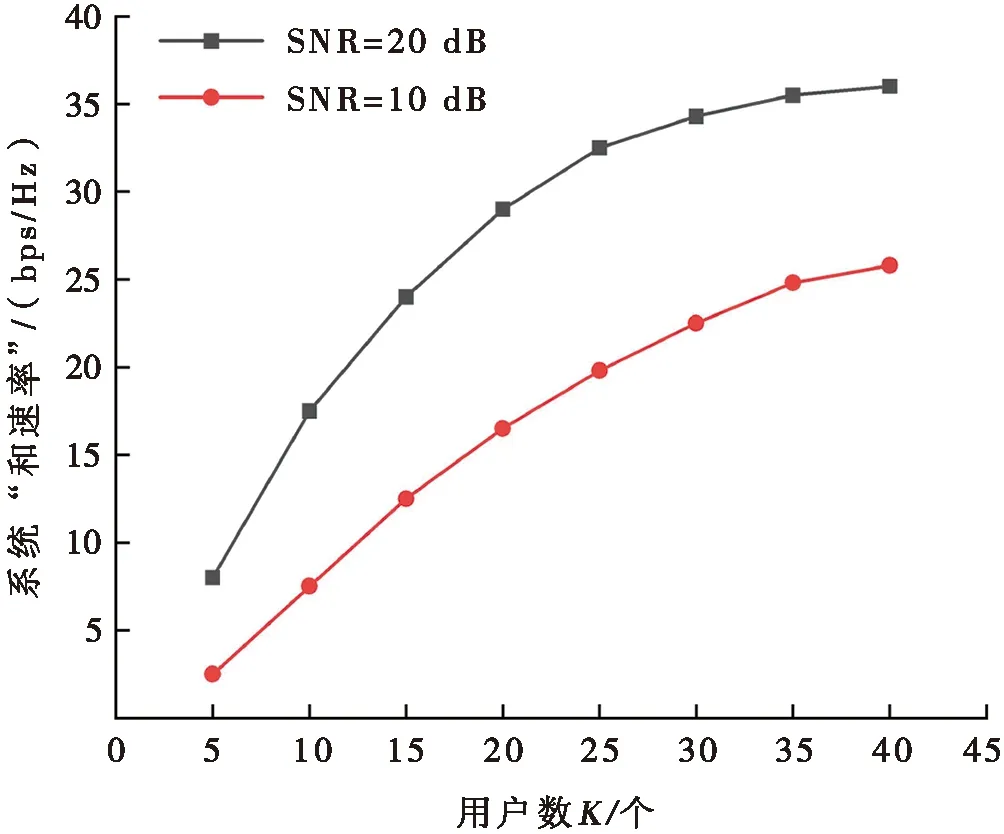
圖3 不同信噪比下的用戶數與信道總傳輸速率關系

如圖4所示，數字波束成形方案具有較低的總發射功率，但是，對于較低的SNR(即10 dB)，波束選擇系統與多用戶數字波束成形系統的總發射功率之間的間隙變小。當SNR為10 dB，用戶數為40時，兩方案總發射功率間隙約為2.35 dB，且該間隙隨用戶數的增大而減小。圖4表明當信噪比低且用戶數較大時，與多用戶數字波束成形方案相比，波束選擇系統可以以較低的系統復雜度提供合理的性能。

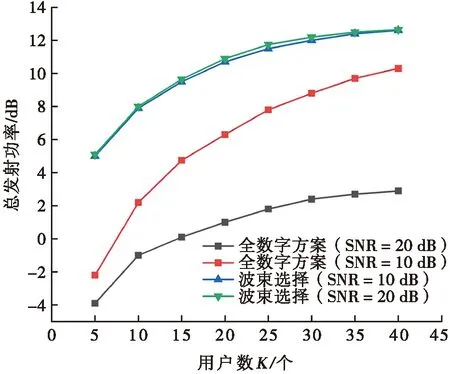
圖4 不同SNR下兩種波束選擇方案的用戶數與發射功率關系

圖5對比了不同的波束選擇方案，全數字波束成形方案系統性能最佳，但其系統開銷也遠高于其他方案，當基站天線數遠大于用戶數時，由于多用戶干擾對于系統性能影響降低，基于壓縮感知的波束選擇方案的性能隨用戶數呈線性增長，其性能介于信干噪比最大化波束選擇方案和基于空間重疊指數波束選擇方案之間。

圖5 不同波束選擇方案的用戶數與信道總傳輸速率關系

4 結束語

本文構建了毫米波無線信道仿真模型，并在模型中融入了大規模MIMO技術與混合波束成形技術。為考察不同波束選擇算法的性能，在確定毫米波無線信道仿真模型時選擇了復雜度較低的RMa-LOS場景。通過仿真工具對所研究方案進行仿真與分析。實驗結果表明，基于壓縮感知的波束選擇方案系統總傳輸速率關于用戶數近似呈對數增長，全數字方案及空間索引方案所需要全信道狀態信息在大規模MIMO系統下會帶來較高的信令開銷，本文所研究的壓縮感知的波束選擇方案系統性能雖然不是最優，但可在明顯節省硬件成本和降低信令開銷的情況下提供較好的性能。