基于一種兩側獨立驅動全驅輪式底盤的轉向性能分析
張明松 ,胡亞朋
(三峽大學機械與動力學院,湖北 宜昌 443002)
隨著科技的不斷進步,人們不斷研究各種大型機械輔助完成公路、橋梁、建筑、地下工程、搶險等重大工程項目。改革開放以來,我國在基礎設施建設方面的投資不斷加大,在這些基礎設施建設中往往需要特種機械車輛的輔助。這為工程機械車輛技術研發的突破提供了有利條件。本文所研究的兩側獨立驅動全驅輪式底盤采用兩側電機獨立驅動模式,接下來將對底盤的合理性進行研究。
1 底盤轉向運動學分析
差速率即兩側獨立驅動全驅輪式底盤的兩側車輪的差速程度。當底盤轉向時,差速率e計算公式[1]為:

兩側獨立驅動全驅輪式底盤轉向過程中,前后軸應該有同一個轉向中心,并且繞著各自的圓周作純滾動。假設在某時刻,底盤以瞬時轉向半徑R1繞瞬時圓心點O轉向,其車速及半徑關系[2]為:
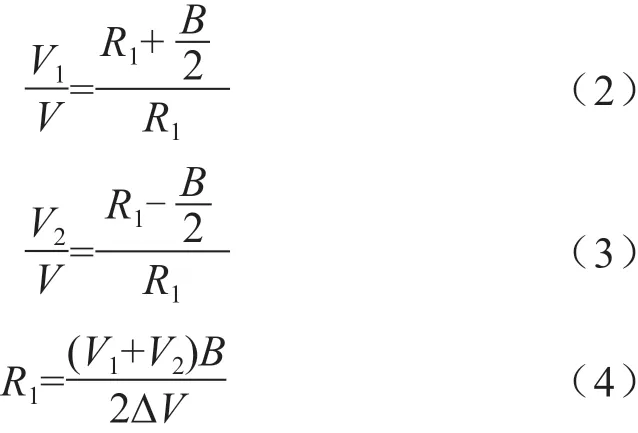
式中,B為兩側車輪的中心距離,單位為m;ΔV為兩側驅動輪輪速之差,單位為m/s;V1為左側瞬時輪速,單位為m/s;V2為右側瞬時輪速,單位為m/s。
2 底盤轉向動力學分析
二自由度動力學模型:兩側獨立驅動全驅輪式底盤在行駛過程中,橫擺運動與側向運動相互影響,故二自由度動力學模型更符合兩側獨立驅動全驅輪式底盤的實際運動情況[3]。考慮到本研究的研究模型沒有轉向機構,故不考慮前輪轉向角的影響,根據經典力學理論及輪胎受力情況[4],建立二自由度轉向動力學模型,如圖1所示。
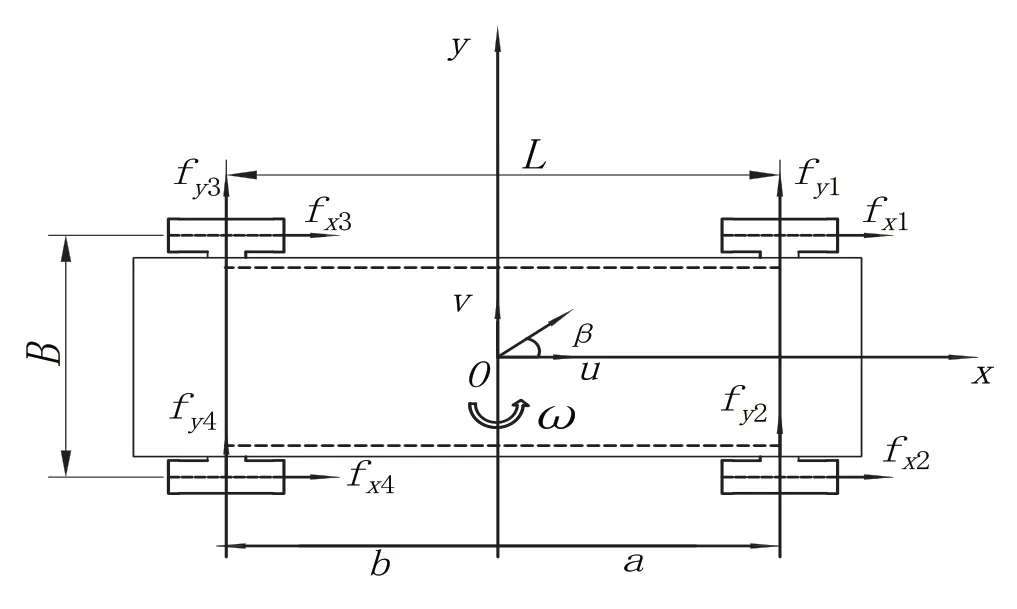
圖1 二自由度轉向動力學模型
側向運動微分方程為:
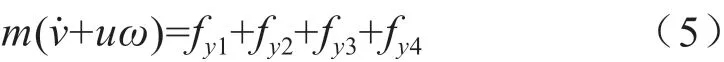
橫擺運動微分方程為:
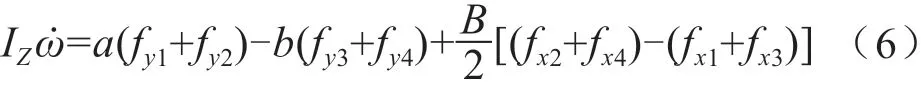
其中,m為整車質量,a和b分別為前后軸到質心的距離,L為前后軸之間的距離,IZ為整車繞Z軸的轉動慣量,u和v分別為車輛的縱向和側向速度,ω為車輛的橫擺角速度,fxi為輪胎受到的縱向力,fyi為輪胎受到的側向力,i=1,2,3,4。
底盤在進行轉向時,主要受到兩種形式的轉向阻力,即地面變形阻力和轉向阻力矩[5]。計算地面變形阻力的方法可參照直線行駛時地面變形阻力的計算方法,設內外車輪受到的地面變形阻力分別為f1和f2。則f1=f2=0.5f G。
在轉向過程中,由于內外側車輪的轉速不同,地面對輪胎產生的摩擦力也不同[6]。輪胎將受到更大的阻力,所以需要取內外側電機功率差更大的值,而不同的轉向半徑需要電機輸出的功率及底盤消耗的功率也不相同。研究轉向半徑與功率差值之間的關系,可對轉向系統的性能進行優化并為轉向過程控制提供理論依據。接下來對兩種情況下底盤轉向時輪胎的受力情況進行分析。
2.1 原地中心轉向
原地中心轉向時,兩側電機處于驅動狀態。兩側電機工作狀態為:輸出的轉矩和轉速大小相等,方向相反。此時轉向半徑在0~B/2之間。實現該類轉向的機械傳動系統是十分復雜的,而且系統本身控制比較復雜[7]。采用電機驅動可靈活實現正反轉并精確控制電機轉速及轉矩,實現底盤自身靈活運動。底盤轉向時輪胎的受力情況如圖2所示。
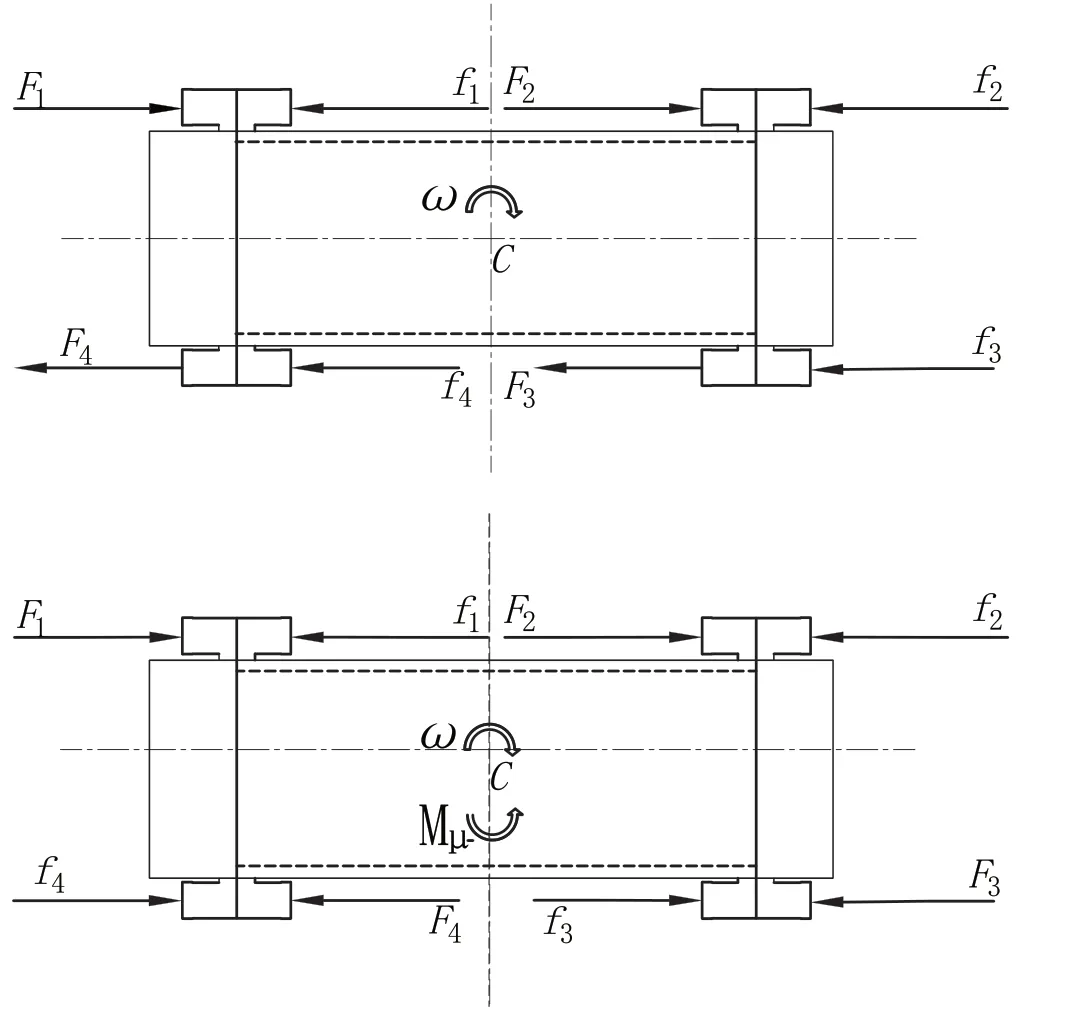
圖2 底盤轉向時輪胎的受力分析
根據勻速轉向的條件可推出:
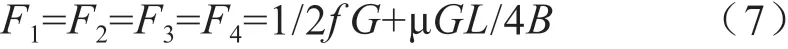
此時內外側車輪受到的驅動力的大小相等,當轉向半徑R=0時,車輪受到的轉向阻力矩最大,此時內外側電機輸出的扭矩相對其他轉向過程電機輸出的扭矩更大。中心轉向可以減少底盤轉向時的占地面積,使底盤轉向更加靈活。
2.2 車身外一點轉向
當底盤以車身外一點轉向時,輪胎的受力分析如圖3所示。外側電機輸出電動轉矩,內側電機工作在發電機狀態,產生制動轉矩[8]。相應的外側車輪受到驅動力F1和F2,由于前后輪之間用鏈傳動連接,故前后輪受到的驅動力大小相等。內側受到制動力F3和F4,同理F3=F4。根據底盤勻速轉向的條件,可以得到:

圖3 底盤以車身外一點轉向時輪胎的受力分析
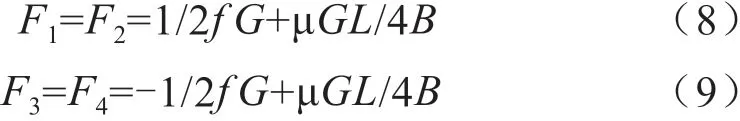
3 建立底盤模型
在現在產品的研發過程中,通常先利用計算機仿真軟件對汽車的整體和零部件進行建模仿真,這使得在研發的初期階段能夠及時發現設計中存在的問題,修改零部件參數并調整控制策略。因此,接下來本文將利用計算機仿真技術對雙側電驅動車輛的整車轉向動力學性能進行建模和仿真[9]。
3.1 底盤參數
通過上文對底盤進行動力學及運動學理論分析后,得到其運動方程,基于理論公式,通過Carsim軟件搭建底盤仿真模型,具體的結構參數如表1所示。

表1 底盤結構參數
3.2 Carsim建模
通過Carsim交互式仿真平臺,對底盤結構參數進行設置,具體情況如圖4所示。設置道路工況為雙移線,如圖5所示。
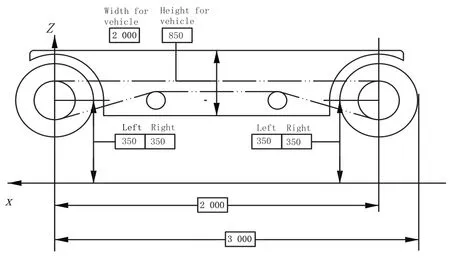
圖4 底盤結構參數

圖5 雙移線道路
4 仿真分析
為了分析前面所建立的底盤模型的操縱穩定性能,根據國家標準對模型進行雙移線試驗以及轉彎半徑試驗,并進行模擬仿真,根據仿真結果對整車操縱穩定性進行評價[10]。結合所設計的車輛參數,確定本車的試驗車速為10 km/h、25 km/h、40 km/h,試驗道路附著系數為0.85,對本車進行雙移線試驗。
4.1 橫擺角速度
通過雙移線仿真試驗測得車輛在10 km/h、25 km/h、40 km/h的車速下行駛時的橫擺角速度對比情況,如圖6所示。由圖6可知車速為10 km/h時,底盤在轉彎時的橫擺角速度最大值為20 rad/s,此時底盤的側向加速度為0.25 g。車速為25 km/h時,底盤通過雙移線時的最大橫擺角速度為32 rad/s,此時底盤的側向加速度最大值為0.43 g。當底盤以40 km/h行駛時,底盤通過雙移線時的最大橫擺角速度為38 rad/s,此時底盤的側向加速度為0.8 g,超出預設范圍,底盤的穩定性變差,會導致車輪側滑,最終造成側翻。因此可以得出,該底盤最高車速在小于25 km/h時,其操縱穩定性能可控制在較理想的范圍內。
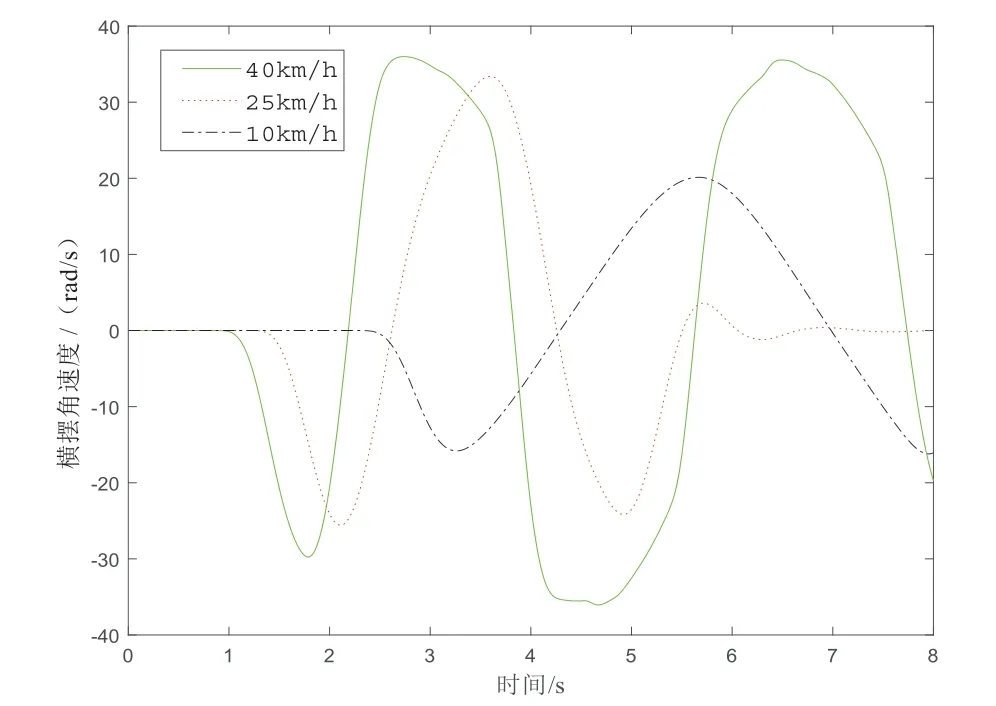
圖6 橫擺角速度對比圖
4.2 轉彎半徑
最小轉彎半徑試驗,即當底盤兩側車輪按照一定差速率行駛時,隨著車速增加,在保證底盤不發生側滑的前提下,所能通過的最小轉彎半徑。最小轉彎半徑越小,底盤行駛時的機動性能越好。車輛由開始加速至最大穩定車速25 km/h時,車輛通過的轉彎半徑及側向加速度對比如圖7、圖8所示。
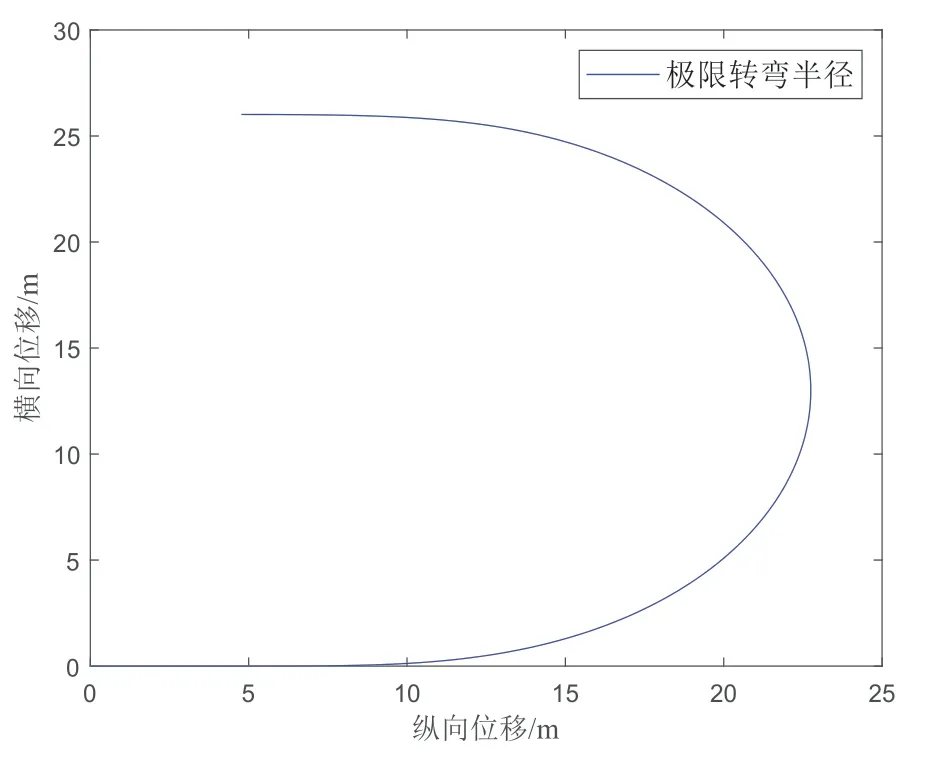
圖7 轉彎半徑
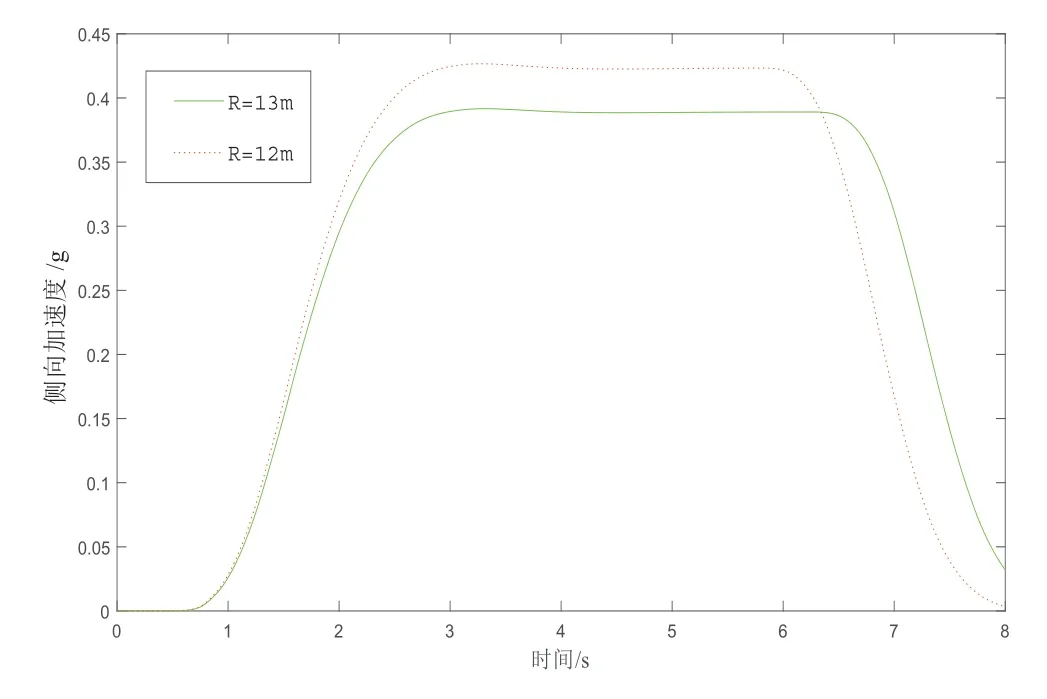
圖8 側向加速度對比
由圖8可知,當底盤的轉彎半徑R>13 m時,底盤通過此半徑的側向加速度小于0.4 g,當底盤的轉彎半徑R<13 m時,側向加速度大于0.4 g,此時輪胎與地面將產生滑移,因而根據工程車輛底盤設計要求,此底盤的最小轉彎半徑不應小于13 m。
5 結論
本文以二自由度兩側獨立驅動全驅輪式底盤為研究對象,建立了底盤的動力學及運動學理論模型,并對底盤的參數進行設計,通過Carsim仿真軟件對底盤的合理性進行驗證。分析得到以下結論:
1)底盤的行駛穩定性受速度、質心高度、轉彎半徑等因素影響,其中速度和轉彎半徑變化對底盤的穩定性影響較大。當底盤速度大于設定值25 km/h時,底盤在雙移線試驗中的側向加速度大于0.4 g,底盤的穩定性變差。
2)當轉彎半徑R<13 m時,輪胎與地面將產生滑移,導致底盤側滑。故該底盤的最高車速不應超過25 km/h,以最高車速行駛時,轉彎半徑不應小于
13 m。

