可變脈沖控制下的多智能體系統固定時間一致性研究

隆騰，楊莎莎，王茜竹

（1.重慶郵電大學 通信與信息工程學院，重慶 400065；2.重慶郵電大學 計算機科學與技術學院，重慶 400065）

0 概述

近年來，多智能體系統（Multi-Agent Systems，MASs）的分布式控制與優化廣泛應用于無人機、機器人集群的協同作業［1-3］，但在已有研究中MASs 通信環境通常為理想狀態，然而在真實網絡環境中系統可能會受到環境干擾的隨機變化［4-5］，例如信息傳輸的隨機噪聲干擾、隨機故障等。而且由于外部工作環境復雜，智能體之間在傳輸過程中往往會受到外部隨機波動等概率因素引起的隨機擾動［6-7］，因此一致性問題隨著研究的深入逐漸引起關注［8］。

目前，有許多控制方法可以實現MASs 一致性，如自適應控制［9］、牽引控制［10］、魯棒控制［11］等。脈沖控制作為一種有效的非連續控制策略，只允許每個節點在脈沖瞬間傳輸信息，這大大降低了網絡的通信負載。文獻［12］提出基于固定拓撲、切換拓撲和外部干擾的3 種脈沖控制協議，以實現連續時間網絡的一致性。文獻［13］研究具有輸入飽和度的分布式脈沖一致協議，以漸近地保證動態系統的動態一致。但是，上述研究對于脈沖間隔的設定比較固定，也就是預先設定脈沖間隔。由于實際系統的物理約束，因此智能體之間的信息交換不能準確地在預先設定好的脈沖采樣時間內發生。為了獲得更靈活的脈沖采樣時刻，文獻［14］提出在脈沖時間窗內約束脈沖輸入的可變脈沖控制策略。文獻［15］研究了有向網絡拓撲中MASs 具有領導-跟隨者一致的可變脈沖控制策略，這種策略允許脈沖采樣時間隨機發生在脈沖時間窗內，從而使得系統更加適用于現實場景。

雖然上述工作研究了如何降低系統的通信負載并使其更加適用于現實情況，但是所用方法為漸近一致性，忽略了系統達到一致時所需要的時間。與漸近一致性相比，有限時間一致性提高了系統的收斂速度［16-17］。但是，有限時間一致性的時間計算需要依賴于系統的初始狀態。因此，有研究人員提出了固定時間一致性，使系統的一致性時間不再依賴于初始條件［18-19］。另外，在實際的通信環境中，由于外部干擾或鏈路故障，智能體之間的通信拓撲結構可能會改變［20-21］，因此可以引入切換拓撲結構。目前，關于脈沖控制與固定時間一致相結合的研究采用單階控制，然而由于MASs 應用場景的復雜性和多樣化，單階控制的收斂狀態相對單一，靈活性較差。

受到上述工作的啟發，本文研究可變脈沖控制和固定時間一致性相結合的雙階控制（Two-Stage Control，TSC）策略。TSC 策略根據實際應用需求進行動態調整收斂周期，通過增加脈沖個數來應對通信資源稀缺的問題，但如果系統需要獲得更快的收斂速度且網絡條件良好，則可以適當減少脈沖數量。通過在領導-跟隨者情況下的具有切換拓撲的MASs數值仿真案例以驗證理論結果的有效性。

1 預備知識與系統模型

假設1在Gσ(t)中存在有向生成樹并且領導者節點為根節點。

假設2設φ(·)和h(·)為非線性函數并滿足以下Lipschi tz 條件：

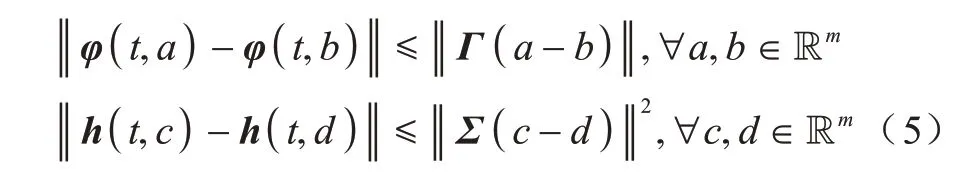
在式（5）中：Γ和Σ為已知常數矩陣；‖ · ‖表示歐氏范數。

假設3 可變脈沖控制階段遵循如下規則：

2 理論分析與主要結果

本文設計將可變脈沖控制和固定時間一致相結合的TSC 策略，因此給出如下有效的TSC 協議：

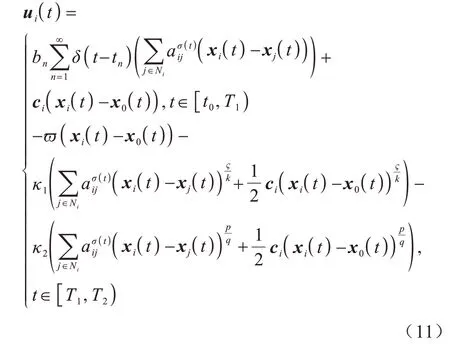
在式（11）中：δ(t-tn)為沖激函數；bn為脈沖控制增益；脈沖序列0 ＜t0＜t1＜…＜tn＜…并且+∞；定 義并設xi(t) 為右連續；?表示固定時間階段的控制參數；?、k、p、q都為奇數并滿足?＜k和p＞q；T1表示脈沖控制階段和固定時間階段的分界時間，也表示固定時間階段的初始時間；T2表示系統達到一致時具體的預設時間。

如圖1 所示，系統收斂周期分為兩個階段，分別是可變脈沖控制階段和固定時間連續控制階段。為了進一步提升系統收斂速度，并準確計算出系統的預設時間，本文在有限時間一致控制器的基礎上進行改進引入了固定時間一致性理論，與文獻［16-17］相比，本文采用的固定時間一致的預設時間與系統的初始條件無關，該方法能夠根據相關參數準確地計算出系統達到一致時的時間，比有限時間一致更準確。此外，本文中的固定時間一致控制協議沒有使用會引起系統顫振的符號函數，這對系統的穩定性會有較大的提升。

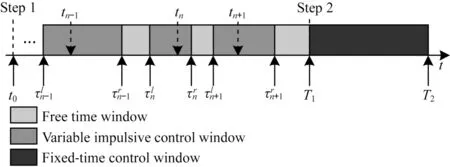
圖1 TSC 示意圖Fig.1 Schematic diagram of TSC

在第一個控制階段，結合控制器式（11）和系統式（1），可以將脈沖控制系統定義如下：

若上述條件滿足，則系統式（1）可以通過控制器式（11）達到具有領導-跟隨者的固定時間一致。

證明在第一個控制階段t∈[t0,T1)，定義如下Lyapunov 函數：

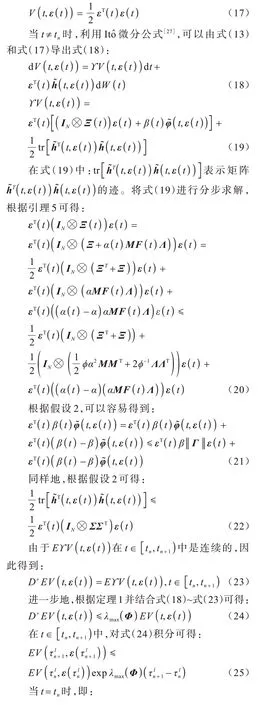
在式（33）中：tω表示脈沖發生的次數；T1是固定時間階段的起始時間和在整個脈沖周期中所經過的時間，為中的隨機值；V(T1,ε(T1))表示固定時間階段的初始狀態。本文根據實際應用場景設置ω的個數，則脈沖個數可以決定T1的大小。

不等式（26）中的特征值θn表示系統中的全局信息會有n次脈沖采樣。從式（27）到式（29）可以看出，當系統時間達到tn時，則系統會得到特征值θ，也就意味著系統會觸發脈沖采樣；如果系統時間沒有超過脈沖時間窗口的脈沖控制時間，則系統不會觸發脈沖采樣。例如，若選擇5 個脈沖采樣，則ω=5，則通過式（33）脈沖推導過程可以改寫為：那么第5 個脈沖就會在第5 個脈沖時間窗的左端點到第6 個脈沖時間窗的左端點，也就是在內發生，利用條件進行反 推，可得該式中特征值θ有5 個，則系統在達到第6 個脈沖時間窗的左端點時發生5 個脈沖采樣。

本文主要是利用TSC 策略對收斂周期進行動態調整，脈沖數量減少的觸發條件可以依據式（26）～式（33）的推導過程進行判定，主要是對ω的大小進行設定。此外，本文主要根據現實應用要求進行選擇脈沖采樣數量以應對系統網絡條件：若網絡通信資源比較豐富，則可以減少脈沖數量以更快地提升系統的收斂速度；若通信資源較稀缺，則可以適當增加脈沖數量以減少通信量。因此，本文研究內容主要為減少系統通信成本的同時提升一致性速度提供一種新思路。

在固定時間控制階段的系統誤差可以表示如下：

根據定理1 和式（23）得到式（37）。進一步地，根據（37）可以得到式（38）。根據引理1～引理5 可得式（39）。

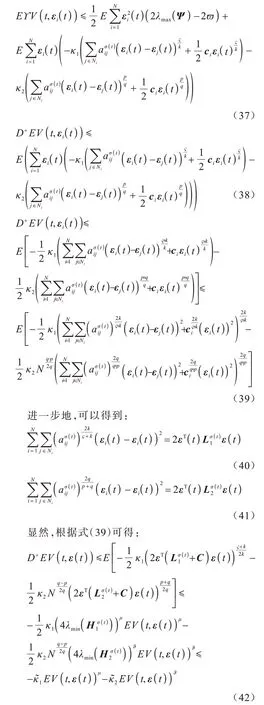
因此，根據引理1，可以得到系統式（1）的一致時間：

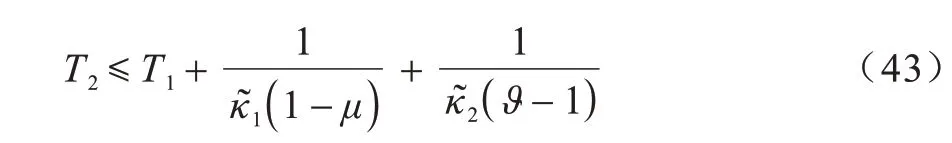
在式（43）中：T2是脈沖控制階段和固定時間階段的整個收斂時間。當t≥T2時，可以得到EV(t,ε(t)) ≡0。因此，具有隨機擾動的MASs 能夠達到全局固定時間穩定。

3 數值仿真

本節給出一個領導-跟隨者的仿真案例，證明了控制協議式（11）的有效性和可靠性。

考慮具有5 個智能體的MASs 參數設置如下：

從上述公式中可以得出Γ=diag{0.5,0.5,0.8}以及Σ=diag{0.2,0.4,0.6}。設伯努利分布的隨機變量α(t)和β(t)滿足α=β=0.5。設?=2，那么通過簡單的計算得到λmax(Φ)=23.415 9，λmax(Ψ)=31.740 2。

系統的通信拓撲圖如圖2 所示，其中，0 節點為領導者，其他節點為跟隨者。

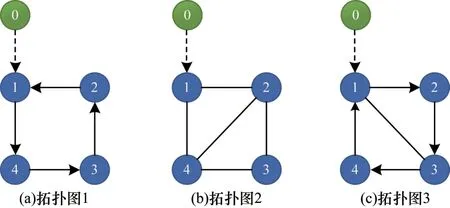
圖2 通信拓撲圖Fig.2 Communication topology

根據定理1 以及已知參數，設bn=-0.4，ζ=1.01。通過簡單的計算得到θn=0.866 5，則脈沖時間窗上限為簡單起見，選用=0.005 5。如圖3 所示，脈沖采樣時刻在脈沖時間窗內隨機發生，并分別設定6 個和9 個脈沖采樣時刻，即ω=6 和ω=9。設切換信號為σ(t)=(nmod 4),t∈[tn,tn+1)。

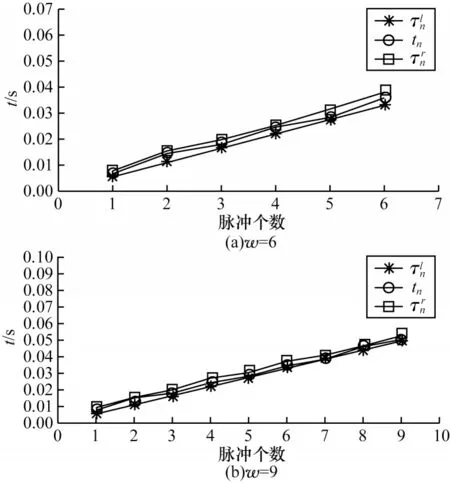
圖3 脈沖時間窗與脈沖數量的關系Fig.3 Relationship of the impulsive time window and the number of impulsive

設定所有智能體的初始狀態值x0=[0.1,0.2,-0.3]T、x1=[5.5,3,4.6]T、x2=[-3.9,-2.8,4.3]T、x3=[ -5.7,3.5,-6.2]T、x4=[4.9,-3.2,-2.4]T。TSC 收斂過程如圖4、圖5 所示（彩色效果見《計算機工程》官網HTML 版），可以看出t6=T1=0.034 4，t9=T1=0.050 8。在固定時間控制階段，設?=35、κ1=2、κ2=2.5、?=1、k=3、p=5、q=3。根據式（43）可以計算出系統的一致時間為T2=2.354 1，從圖4 和圖5 的結果可以看出，系統的收斂時間要遠小于T2，并且可以根據脈沖個數對收斂周期進行動態調整。當設定的脈沖采樣數量較多時，系統的收斂時間會更長，但是減少的通信量更多，通信資源的消耗更少；當設定的脈沖采樣數量較少時，則收斂周期會更快地進入第二階段，隨之收斂時間也會更短。這也進一步驗證了雙階控制對于動態調整系統收斂周期的有效性和準確性，因此，具有隨機擾動的領導-跟隨者MASs 可以在控制協議式（11）下達到固定時間一致。

單階控制、可變脈沖控制和固定時間連續控制下得到的三維狀態值以及狀態誤差如圖6～圖8 所示（彩色效果見《計算機工程》官網HTML 版）。由圖6 可以看出，單階控制收斂速度要稍快，但單階控制的收斂狀態比較單一，無法改變脈沖采樣個數。由圖7 可以看出，單一的脈沖控制可以減少通信成本，但是漸近一致性使得該方案不適用于現實場景，而TSC 策略的收斂時間相比于單一可變脈沖控制減少了0.07 s。由圖8 可以看出，單一固定時間連續控制有較快的收斂速度，但是連續不斷的通信交互使得通信資源的消耗也不斷增加，而TSC 策略的通信次數相比于單一固定時間連續控制分別減少了6～9。

因此，通過與圖4 和圖5 的雙階控制以及圖6～圖8的單階和單一控0 制的對比可以看出，本文提出的TSC策略是有效的，符合實際應用場景。

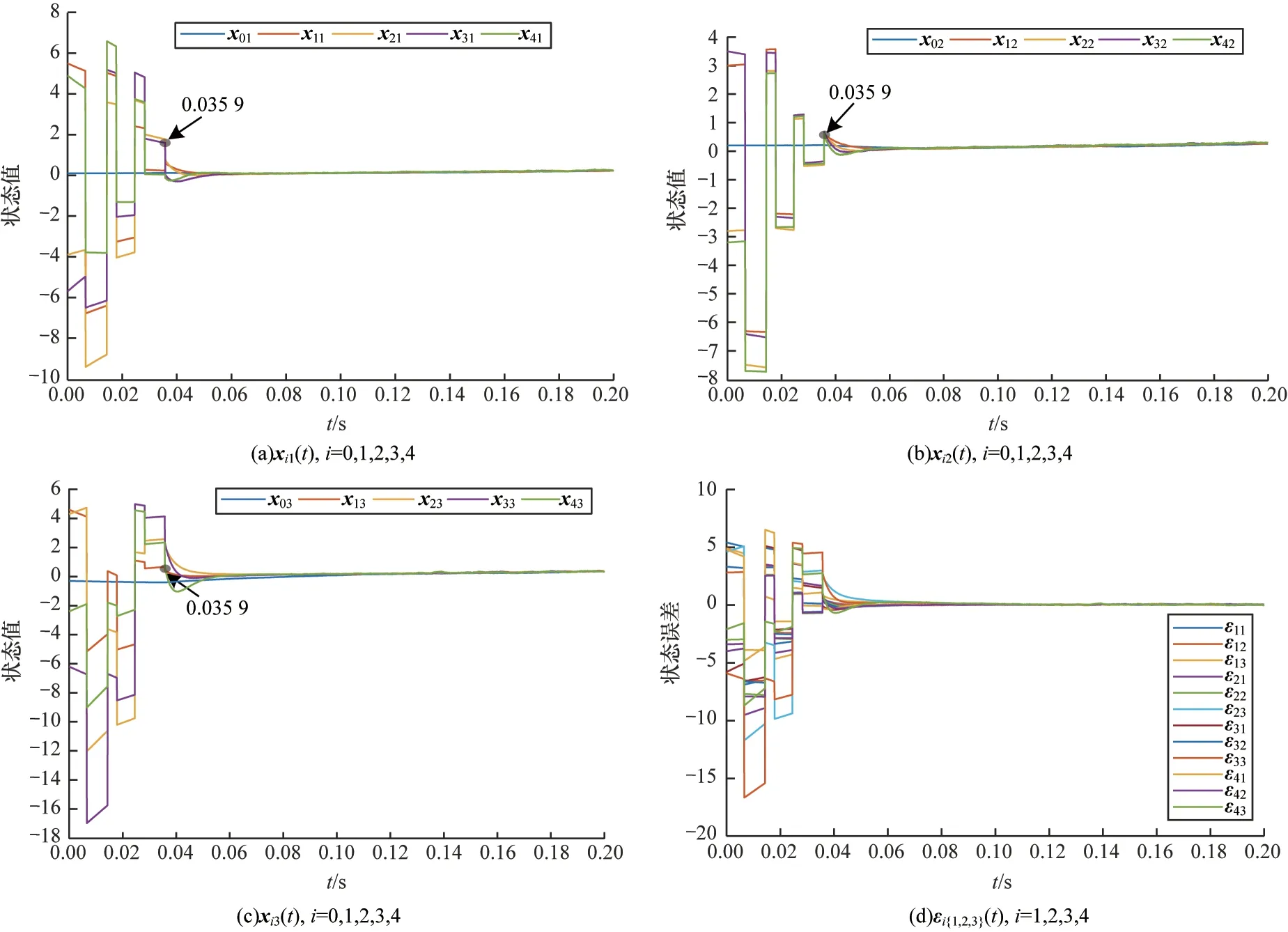
圖4 6 個脈沖控制下得到的三維狀態值以及狀態誤差Fig.4 3D state value and state error obtained via the six impulsive controls

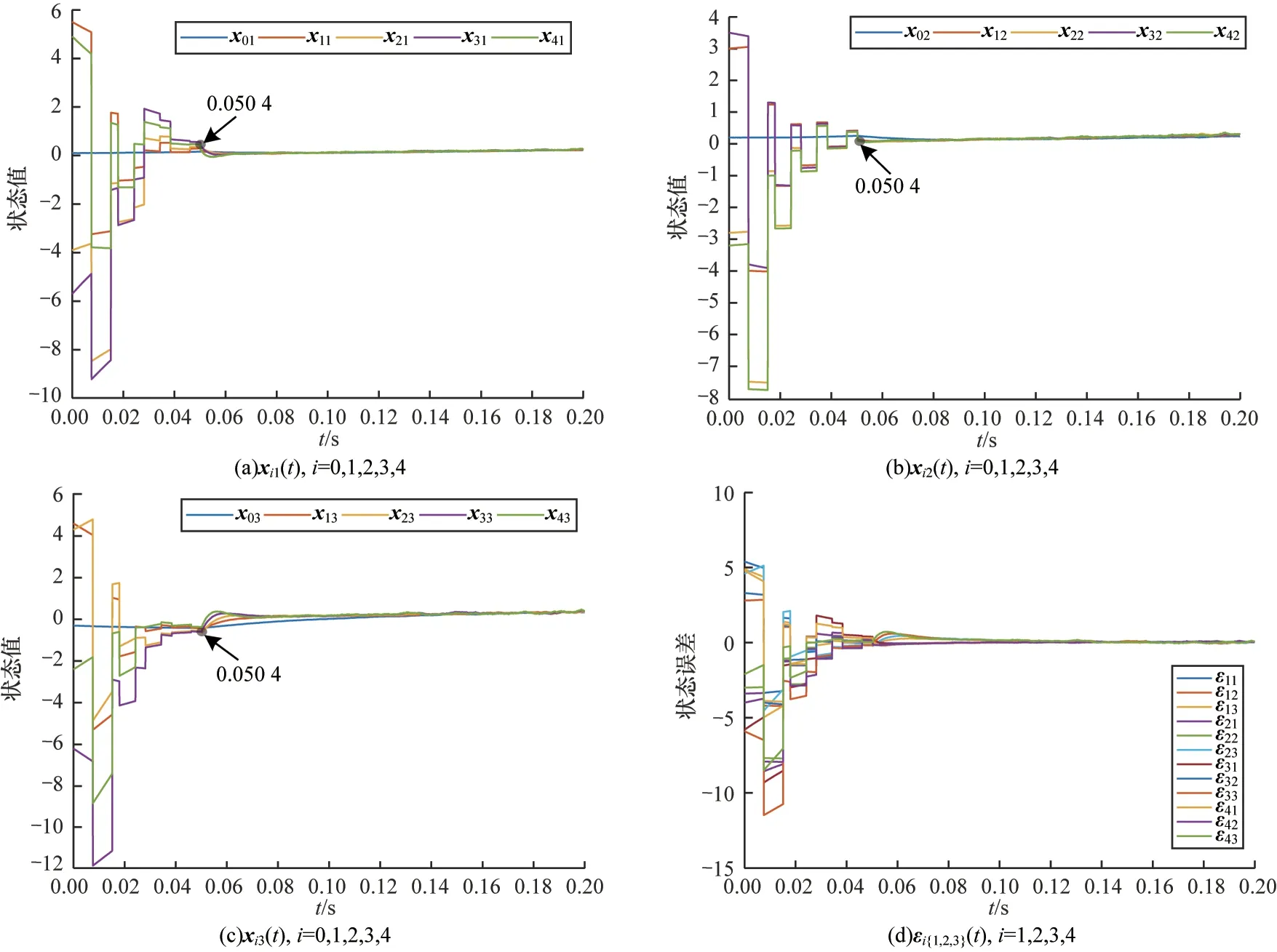
圖5 9 個脈沖控制下得到的三維狀態值以及狀態誤差Fig.5 3D state value and state error obtained via the nine impulsive controls

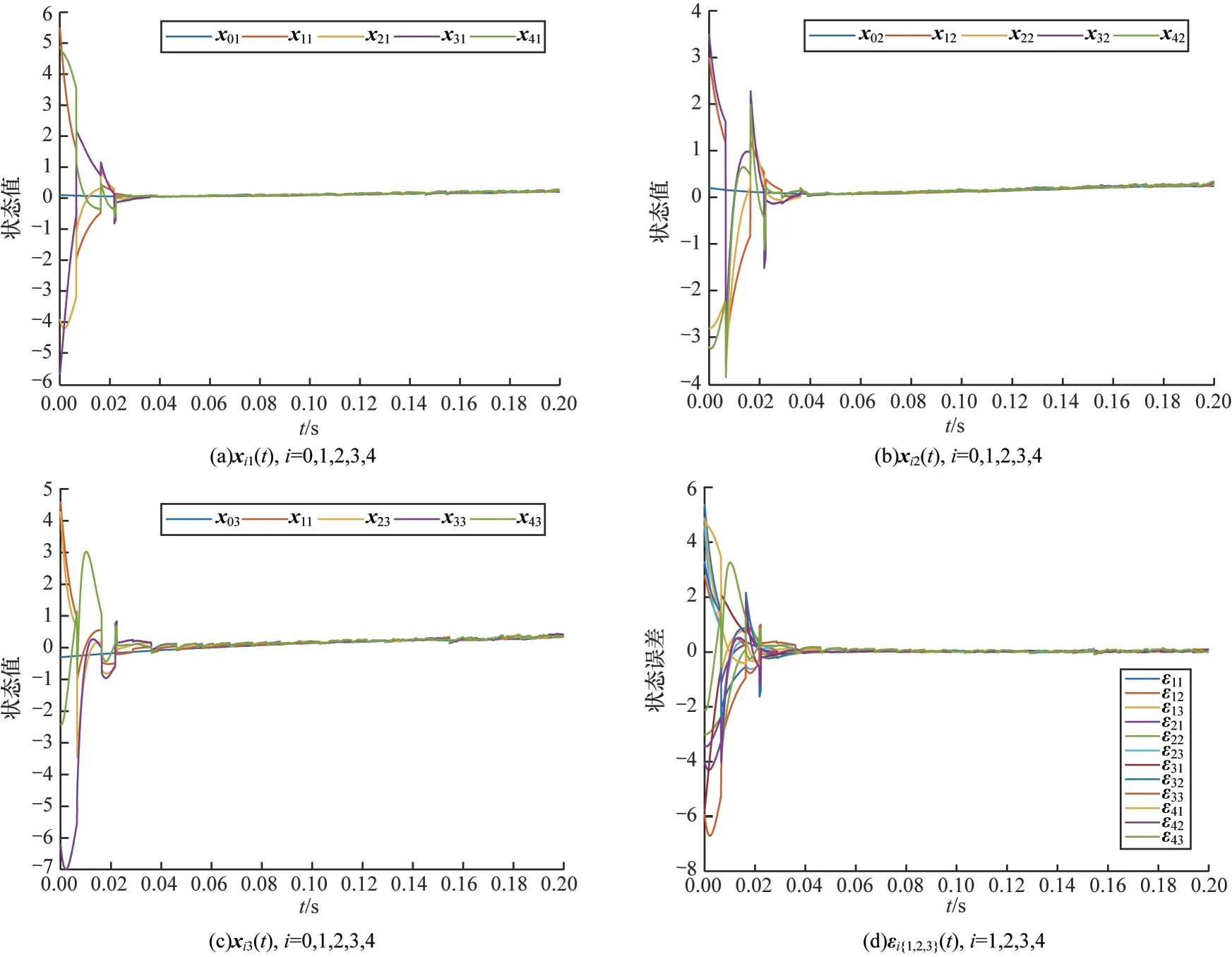
圖6 單階控制下得到的三維狀態值以及狀態誤差Fig.6 3D state value and state error obtained via single-stage control

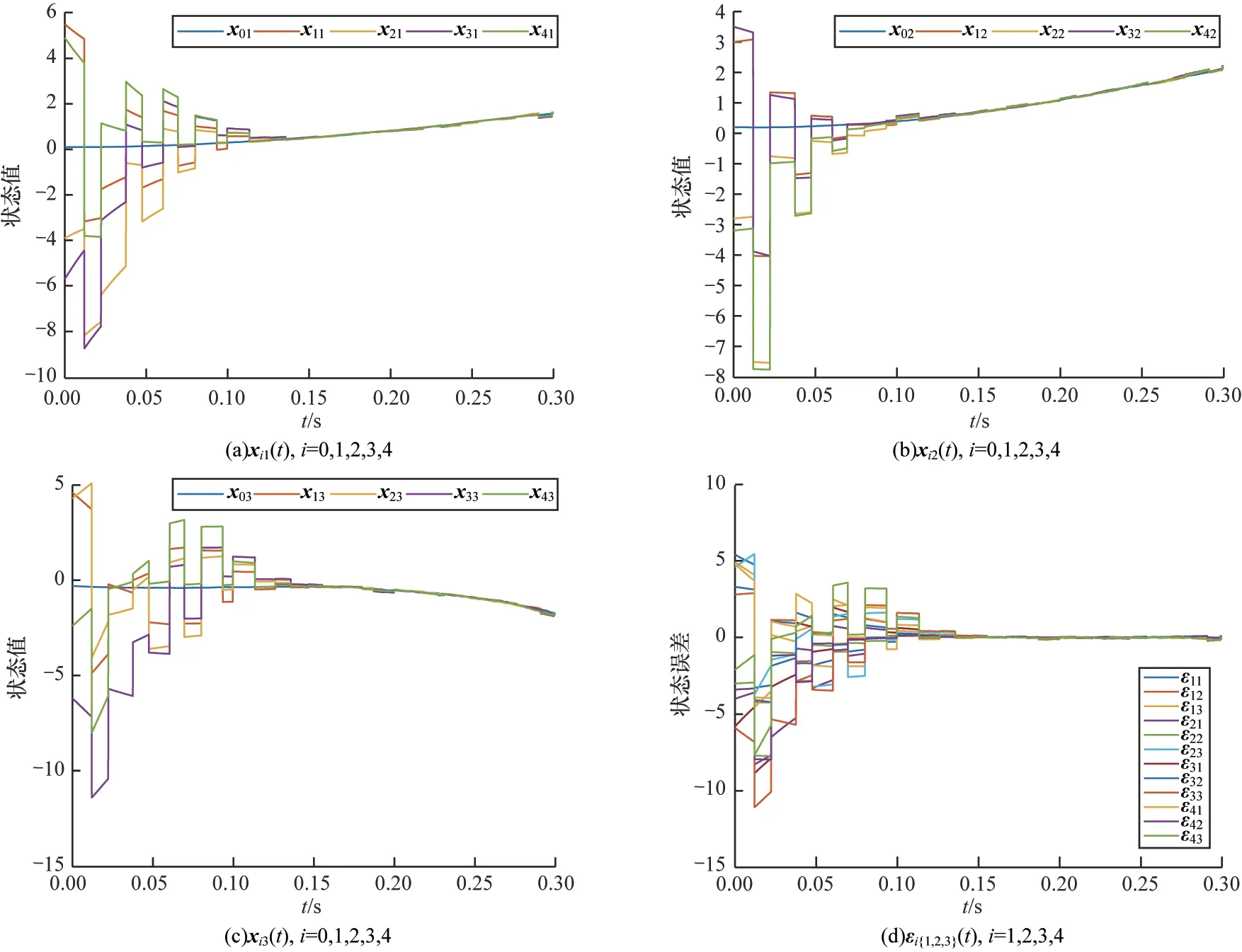
圖7 可變脈沖控制下得到的三維狀態值以及狀態誤差Fig.7 3D state value and state error obtained via variable impulsive control

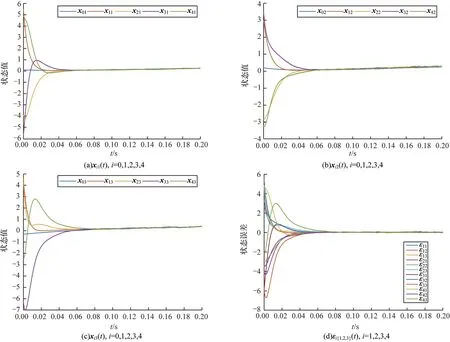
圖8 固定時間連續控制下得到的三維狀態值以及狀態誤差Fig.8 3D state value and state error obtained via fixed-time continuous control

4 結束語

本文通過分析并研究具有隨機擾動的多智能體系統的固定時間一致性問題提出TSC 策略，將整個控制周期分為可變脈沖控制階段和固定時間一致控制階段。通過數值仿真案例驗證了TSC 策略的有效性，并表明其為不同通信網絡條件下的應用場景提供了一個新的研究視角。由于本文引入可變脈沖控制，這對脈沖采樣的靈活性有較大提升，但是脈沖觸發時間主要是在脈沖時間窗范圍內隨機發生，可變脈沖控制難以估計脈沖采樣時間，對于最終結果的可控程度會產生一定的影響，因此后續將進一步探索可控性更高的脈沖控制策略以及二階多智能體系統。