線性代數教學中的引例設計*

葉 昌 潘 陽

（1.湖州師范學院 浙江湖州 313000；2.合肥學院 安徽合肥 230601）

引言

線性代數是應用型本科高校必修的一門重要基礎課。它不僅能夠培養學生嚴密的邏輯思維能力，而且也為與之相關的課程開展提供必備的數學基礎。線性代數知識除了服務數學專業課程，也為機械、計算機、物理、經管等需要建立數學模型解決實際問題的學科課程奠定了一定基礎。該課程目的是使學生掌握線性代數的基本知識、計算方法，通過整個課程體系的構建，達到學生能在后續課程的學習中能運用線性代數來建立專業模型，解決涉及線性代數的專業問題的效果。

由于該課程涉及到的理論知識比較抽象，含有許多復雜的定義和計算，其受眾尤其是工科、經管類專業的學生對該課程知識的理解和掌握有一定難度，使得這門課程在教學過程中不能達到很好的教學效果。因此，在線性代數課程的教學過程中，如果教師能夠通過巧妙的案例來對教學內容進行引入以及闡述，即通過將抽象問題形象化，這不僅能提高課堂的趣味性，也能使學生在形和數的統一中進步會到抽象概念的內涵，從而培養學生思維能力和解決實際問題的能力。

一、線性代數教學中存在的問題

1.學生的數學基礎薄弱且層次不均。

線性代數課程中，存在很多抽象概念和定理，同時具有很強的邏輯性。而對于工科、文科等專業的學生，數學功底較為薄弱，并且學生的數學基礎層次跨度非常大，因此，同樣的教學流程對于不同的學生來說其效果迥異。對于基礎較差的學生，重理論知識的講解通常會使學生難以理解，難以掌握相關知識，并且由于沒有深刻理解知識而導致學完就忘[1]。

2.學生的學習積極性不高。

線性代數課程教學具有邏輯性與抽象性并存的特點。在授課過程中，無法舍去一些關鍵然而復雜的推算過程。并且，由于近年來受到疫情影響，課堂形式中線上線下混合教學模式占比逐漸增大，當理論知識的講解匯集到屏幕上，課程的枯燥性有增無減。因此，學生對該課程的積極性有待提高。

3.課程知識的拓展使用較為局限。

對于工科類，經濟學，物理學等專業，通過線性代數課程的學習，為其建立模型解決相關專業問題打好基礎。由于對課程缺乏興趣以及對理論知識理解不夠透徹，通常不能很好地達到課程知識靈活應用的教學效果，這與應用為導向的線性代數課程之間存在的矛盾亟待解決。

4.思政教育融入課堂困難。

在2016年12月的全國高校思想政治工作會議上指出：要把思想政治工作貫穿教育教學全過程。近年來，國家積極提倡高校課堂融入思政教育，主張在教學中結合思想政治理論，使課程與思想教育并行共進。線性代數課程無論作為專業課抑或是公共課，都服務于各個專業，為高等教育打好基礎，因此，需要教師深入挖掘課程資源。思政教育另一重要目的在于，將課程內容與社會發展相結合，在課程學習后學生能將知識最大程度地內化，再進行落實，服務于社會。但是，如何將思政內容更好地融入課堂教學，不顯生硬，做到潤物細無聲，具有一定的難度[2]。

二、線性代數教學中的引例設計

基于以上考慮，在線性代數課程的教學過程中，需要采用合適的教學方法來應對這些問題。在線性代數課程改革初步探究中發現，案例教學法是提升教學效果的有效方法。針對不同專業的特點進行分析，設計各有特色的課程引例。與學生專業以及生活相關的引例能迅速調動學生的學習積極性，提高聽課效率，激發學習動力。通過有趣貼切案例的引入，學生更容易獲得學以致用的成就感，有助于將課程知識應用到專業學習中，提高解決問題的能力。

k階子式、逆序數、線性方程組的解等都是線性代數的重要內容。本文針對文科專業，設計詩詞游戲引例，講解k階子式；針對工科專業，設計數字華容道引例，講解逆序數的性質；針對教育類專業，設計初中數學題作為引例講解線性方程組的解的情況。通過將抽象問題形象化，不僅提高了課堂的趣味性，也使學生在形和數的統一中進步會到抽象概念的內涵，從而培養了學生思維能力和解決實際問題的能力[3]。

1.k階子式教學的引例設計

定義1.在m×n階矩陣A中，任取k行k列（k≤m，k≤n），位于這些行列交叉處的k2個元素，不改變它們在A中所處的位置次序而得的k階行列式，稱為矩陣A的k階子式。

從定義1中，我們可以發現階子式的概念較為抽象，學生對定義中的任取行、任取列及交叉元素等描述性文字無法形成直觀的印象。誠然，我們可以從低階矩陣入手，通過大量舉例，讓學生被動接受，然后這往往會讓學生喪失學習的興趣，進而會影響學生對該知識點的運用和探索。

奧蘇伯爾認為，有意義的學習必須具備三個條件：其一，學習者表現出一種有意義學習的傾向，即學習者積極主動地把符號所代表的新知識與學習者原認知結構中的適當知識加以聯系的傾向性；其二，學生原認知結構中必須具有適當的“固著點”，即學生的認知結構中具有能和新學習的材料建立聯系的知識點，該“固著點”必須清晰、穩定；其三，所學的材料必須具有邏輯意義，這種邏輯意義指的是所學習的內容本身與人類學習能力范圍內的有關觀念可以建立非人為的和實質性的聯系。

基于上述理論，在階子式的概念教學中，教師可以將漢字作為矩陣元素，先給同學展示圖1中的左圖，請同學觀察其中隱藏的奧秘。通過觀察發現，有十六字經典詩詞“山不在高，有仙則名；水不在深，有龍則靈。”以四行四列的方式散落藏于該矩陣中。學生通過尋找該古詩詞，發現文字分布位置的規律，從而獲得某行某列交叉位置的直觀感覺，最后以此引出階子式的定義。同時，強調當數字作為矩陣元素時，該階子式作為行列式是一個數。類似地，可以利用詩歌、文字嵌入矩陣的方式對行列式、（代數）余子式等概念作相應引入說明。

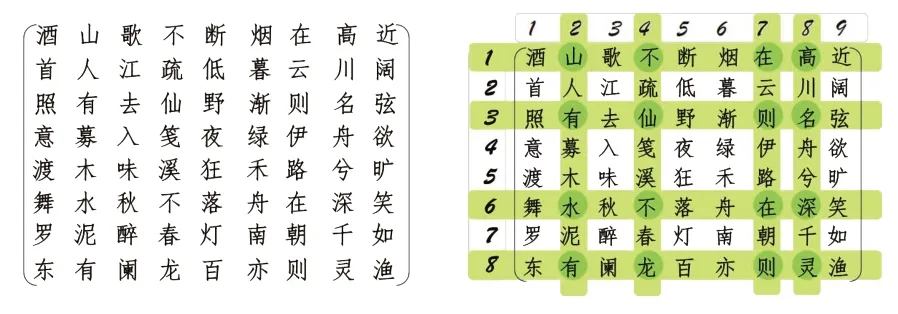
圖1 階子式引例：詩詞游戲

通過詩歌、文字嵌入矩陣的方式進行教學，不僅能夠更好地引起學生的興趣，而且也讓學生感受到我國的傳統文化的優美，增強學生的文化自信和民族自豪感。

2.逆序數教學的引例設計

在線性代數“全排列和對換”這一節，涉及逆序數這個概念。

定義2.當某兩個元素的先后次序與標準次序不同時，就稱這兩個元素組成一個逆序，排列中所有逆序的總數稱為此排列的逆序數。

為了使學生對這個概念有更深刻的理解，即什么樣的次序與標準次序不同，怎么去計算逆序數。為此，我們在教學中引入數字華容道游戲，告訴學生可以通過移動交換華容道里的格子，改變原有的標準排列。

圖2（a）是打亂的排列，圖2（b）是一個標準排列。圖2（a）中14和8這兩個數字，它們的先后順序與原有的標準順序不同，因而14和8就構成了一個逆序。同時，我們需啟發學生，圖（a）中是否存在其他數字也與數字14構成了逆序，引導學生去尋找排在14后面但比14小的數字。如此，就很自然的引入逆序數的計算方法。

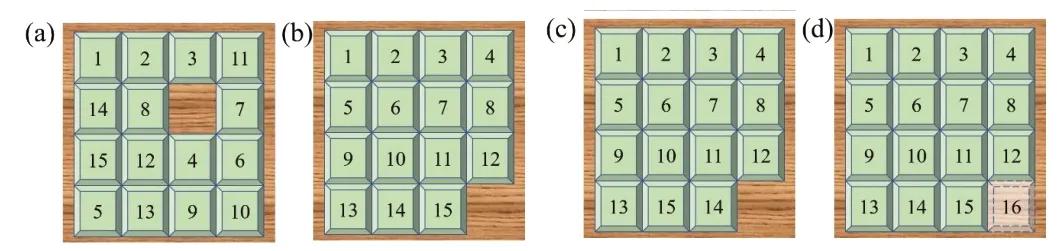
圖2 逆序數引例——華容道數字游戲

我們熟知，對換是可逆的，一個打亂的排列可以按照原先的對換還原到初始的排列。

我們會讓學生思考這樣的問題：①（a）圖需要經過多少次移動格子能還原成（b）圖；②（c）圖能否還原成（d）圖。通過大量舉例，讓學生發現里面蘊含著這樣的事實：①移動次數不唯一，但次數的奇偶性卻是個不變量；②存在不能還原成標準排列的例子。為此，我們引入奇排列和偶排列的概念，即逆序數為奇數的是奇排列，逆序數為偶數的是偶排列，以及一次對換改變排列的奇偶性等。為了讓學生能更好地理解（c）圖為何不能還原成（d）圖，教師需要引導學生將空格位置想象成數字16，如（d）圖，則每次移動就是做一次對換。學生會發現（c）圖不管怎么移動，最后要使空格回到最后的位置總共會經歷偶數次對換。而（c）圖的逆序數是1，是一個奇排列，（b）圖是自然順序，逆序數為0，是一個偶排列。一個奇排列經過偶數次對換只能得到奇排列，不可能會變成偶排列。因此，得到（c）圖永遠不能還原為（b）圖的數學道理，使得學生對排列、逆序數、對換等都有了更深刻的認識和理解[4]。

華容道作為中國民間的益智游戲，蘊含著線性代數的知識，引以此鼓勵學生積極探索我國傳統文化，發掘其中的奧秘。

3.線性方程組解的引例設計

在講解線性方程組的解這一節內容時，重點內容在于掌握n元線性方程組AX=b的解的情況，包含以下3種：

（1）無解的充要條件是系數矩陣的秩小于增廣矩陣的秩；

（2）有唯一解的充要條件是系數矩陣的秩等于增廣矩陣的秩等于n；

（3）有無窮多解的充要條件是系數矩陣的秩等于增廣矩陣的秩小于n。

針對師范專業的學生，在本節內容的教學過程中，以初中數學題為引例的課堂教學效果頗優。引例內容如下：

已知a1+a2=1，a2+a3=2，...，a99+a100=99，a100+a1=100，求a1+a2+...+a100等于幾？

顯然，根據初中數學常用的解題方法，有的學生將所有方程都相加，得到2（a1+a2+...+a100）=1+2+...+100，得到a1+a2+...+a100=（1+2+...+100）/2=2525，有的學生采取間隔取等式的方法來進行計算。其中，一種方法得到a1+a2+...+a100=（a1+a2）+（a3+a4）+...+（a99+a100）=1+3+5+7+...+99=2500；另一種方法為a1+a2+...+a100=a1+（a2+a3）+（a4+a5）+...+（a98+a99）+a100=2+4+6+...+100=2550。三種計算方法似乎都沒有問題，同一數列相加卻得到了三個截然不同的答案，因此可以向學生發問，究竟哪種做法是正確的？題目是否存在問題？該引例為課堂增加了疑點和趣味。據此，課堂自然轉入理論知識的闡述。利用線性代數方程組對該問題進行考慮，100個等式視為一個線性方程組，將其中的元素ai（i=1，2，3，...，100）作為未知數，通過含有100個方程的方程組解100個未知數。通過該課程的學習，可知該非齊次方程組有解的條件為系數矩陣的秩等于增廣矩陣的秩。對于這個方程組，通過圖3對增廣矩陣化行階梯形知其增廣矩陣的秩為100，而其系數矩陣的秩為99，因此該方程組無解，即不存在這樣的一組ai滿足該方程組。所以是題目本身的問題。要使該方程組有解，則應使得增廣矩陣的秩也為99，故可將題中條件a100+a1=100改為a100+a1=50，此時三種方法均解得a1+a2+...+a100=2500。

圖3 線性方程組解的引例——增廣矩陣化行階梯形

該引例不僅讓學生更深刻地理解及掌握了線性方程組的解的條件，而且也讓作為師范專業的學生懂得如何利用線性代數的觀點來看待初中數學問題，懂得“要給學生一杯水，教師要有一桶水”的道理[5]。

結語

本教研論文通過三個引例的設計，實現對線性代數課程中抽象概念的可視化，所引入的三個案例不僅加深了學生對概念的認知，而且同時激發了學生的學習興趣，提升了課堂教學的趣味性。抽象概念趣味化是線性代數教學改革中有意義的探索和實踐。將課程思政自然地融入引例之中，真正做到春風化雨，潤物細無聲。