基于率相關土水特征曲線的邊坡穩定性分析

于建濤

（中鐵第五勘察設計院集團有限公司，北京 102600）

降雨入滲誘發的邊坡失穩現象是一個典型的非飽和土問題。國內外學者對邊坡穩定問題進行了非常深入的研究，提出了很多邊坡穩定性安全系數的計算方法，其中最常用的方法有極限平衡法和強度折減法。采用這些方法去分析非飽和土邊坡穩定時，含水量對土體力學行為的影響研究是其中的一個關鍵問題。降雨入滲使得邊坡非飽和土體的基質吸力降低，進而導致非飽和土的強度降低，降低了邊坡穩定性，誘發滑坡。常規的土坡穩定性分析方法主要是基于飽和土理論和穩定滲流情況，難以反映降雨作用和水位驟降對邊坡穩定的影響，而相當一部分坡體失穩是由于非飽和非穩定滲流引起的[1]。因此有必要采用瞬態或者非穩定滲流模型，對邊坡穩定進行分析預測[2-3]。

在各種邊坡穩定分析方法中，土水特征曲線（Soil-Water Characteristic Curves，簡 稱SWCC）是必不可少的，它描述了土含水量與基質吸力之間的關系，有助于分析土體的力學行為。目前SWCC模型發展較為完善，從早期的經驗模型，到可以反映滯后行為的各種理論模型，以及可以考慮土體變形、溫度等復雜因素影響的模型。但是這些模型大部分是在平衡條件下得到的，現有的研究已經證實，瞬態條件下測得的SWCC與靜態或平衡態測得的SWCC并不重合，SWCC存在明顯的動態效應[4]。Hassanizadeh等[5]的試驗結果顯示，干燥過程中，動態吸力比靜態結果高，而濕化過程中，動態吸力比靜態結果低。

盡管非飽和土瞬態滲流模型也可以反映非飽和土中液體流動和含水量隨時間的變化，但其中所采用SWCC仍是在平衡條件下得到的。Diamantopoulos等[6]發現基于平衡態SWCC的Richard方程無法準確預測分步排水實驗中的水頭變化。此外，這種率效應對水力參數也會產生影響[7]，采用平衡條件下得到的水力參數預測瞬態滲流問題也會使預測結果出現誤差。因此有必要考慮SWCC的率效應對于邊坡穩定的影響，建立基于率相關SWCC的邊坡穩定分析模型。

1 率相關SWCC

1.1 率相關SWCC的理論基礎

劉艷等[8]從熱力學基本平衡方程出發，考慮土體內部的交界面影響，給出了非飽和土流體的熵增不等式

式（1）中第一項是孔隙流體的壓力差，第二項代表宏觀毛細力。Hassanizadeh等[9]指出毛細力本質上是氣液交界面上的一種作用力，并不等同于界面兩側流體的壓力差，并可將宏觀毛細力表示為

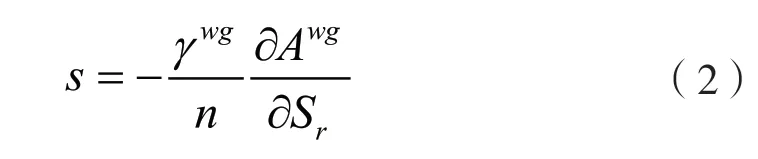
在線性假設條件下，根據熵不等式（1）可以得到液相廣義力與廣義流之間本構關系如下

1.2 非飽和土滲流的基本方程

非飽和土的滲流一般可以采用Richards方程來進行描述，即

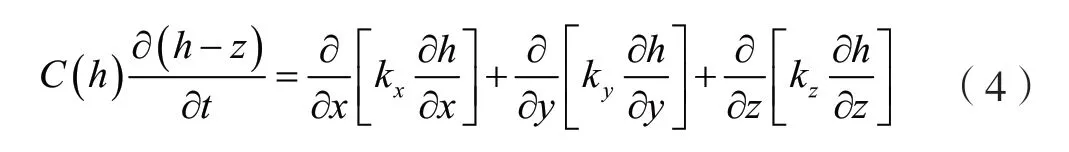
式中：h為總水頭，C（h）為比水容量，kx、ky、kz為各方向的滲透系數，通常可以表示為含水量或吸力的函數，可按式（5）計算

式中：ks為飽和滲透系數。

顯然求解式（4）需借助于SWCC，這里選用VanGenuchen模型，其一般形式可以表示為

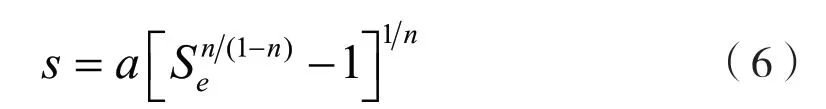
式中：n、a為經驗參數；Se為有效飽和度。

在瞬態入滲的過程中，SWCC具有率效應。將式（6）代入式（3）中可得到率相關的SWCC方程，

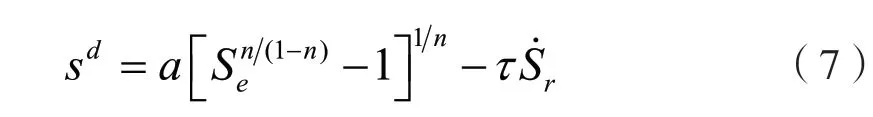
利用式（7），可以計算出考慮率效應后的比水容量C（h）。同時將式（7）代入式（5）中，得到考慮率效應后的滲透系數計算式，即

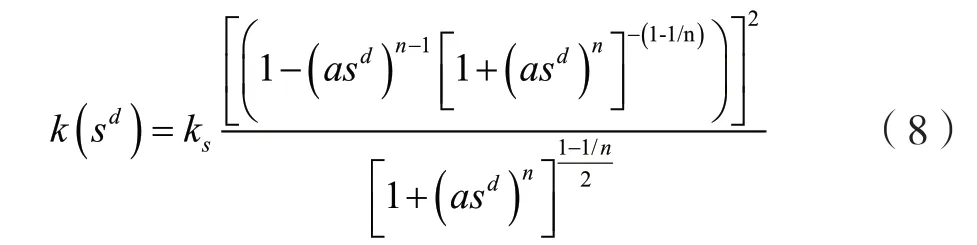
可以看出，率效應不僅影響SWCC，也將改變水力參數，在分析土坡穩定時，有必要考慮這種影響。

2 瞬態入滲邊坡安全系數

2.1 抗剪強度準則

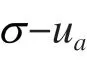
如果考慮SWCC的率效應對安全系數的影響，需將式（7）代入式（9）中，可以得到即得到考慮率效應的土體強度準則，以下基于該強度準則，計算邊坡的安全系數。

2.2 安全系數計算模型

目前已有很多計算邊坡安全系數的方法，比 如 瑞 典 法、Bishop法、Janbu法、Spencer法、Morgenstern-Price法、Sarma法等。本研究采用基于率相關的SWCC來計算安全系數，并與現有方法計算結果進行比較，這里選用Bishop條分法。非飽和土邊坡受力分析見圖1。

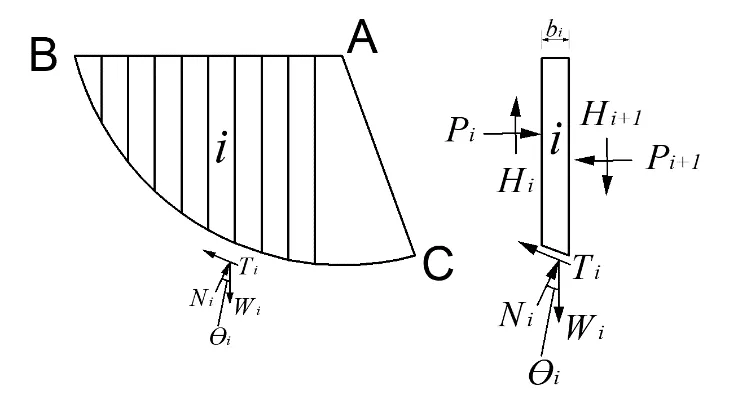
圖1 簡化Bishop法計算受力圖

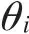
安全系數等于滑動面上的抗滑力除以下滑力，假設氣壓保持為大氣不變，利用式（10）可以得到下滑力為

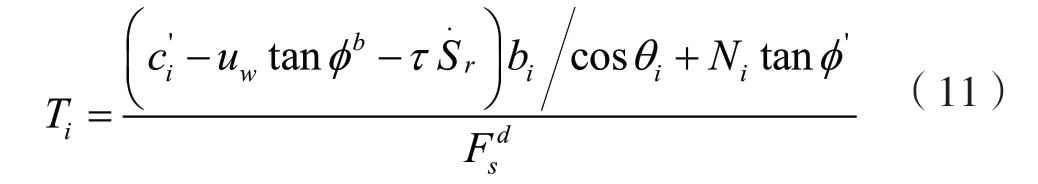
由靜力平衡條件∑Fy=0，ΔH=Hi+1-Hi得

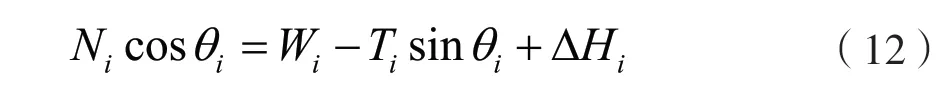
利用式（11）和式（12），消去Ni可得式中

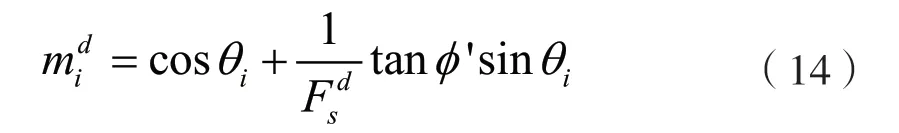
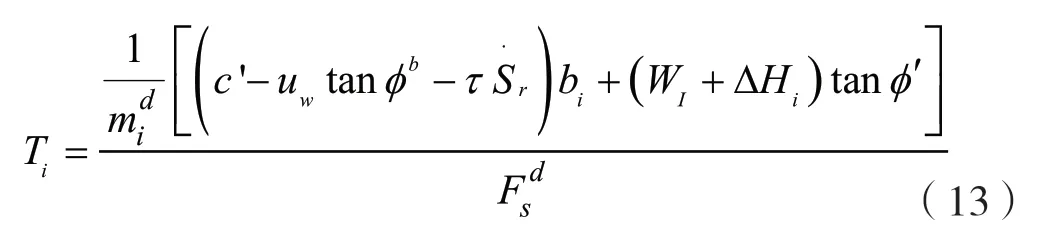
再由靜力平衡條件∑Fy=0，ΔPi=Pi+1-Pi得

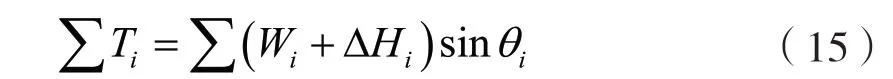
對于整個滑動體來說ΔPi=0，且將式（12）帶入式（15）可以得到

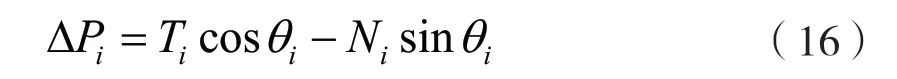
將式（16）帶入式（13）可以得到率效應影響的非飽和土邊坡的安全系數為

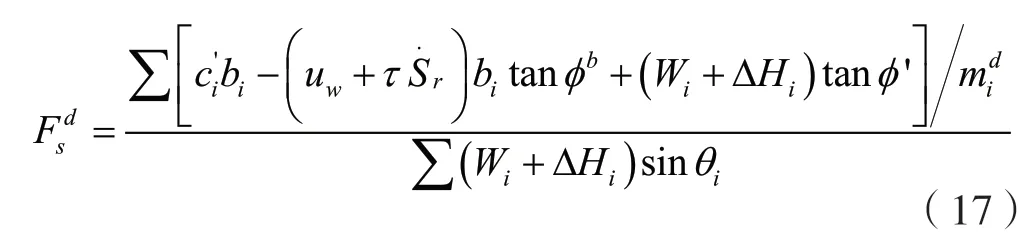
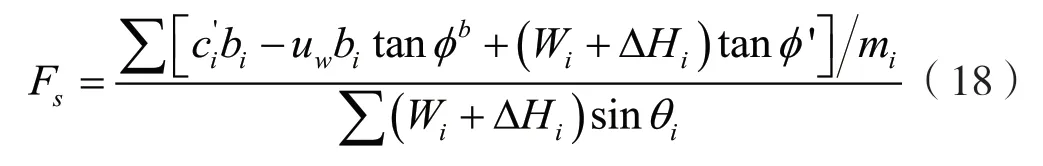
3 計算案例

3.1 計算模型及參數

為分析率相關SWCC對計算邊坡穩定性安全系數的影響，選取典型的邊坡進行計算，邊坡模型如圖2所示。坡高為10 m，坡度為37°。邊坡左側水位高為14 m，右側水位高3 m，左右兩側水位以上為零流量邊界。

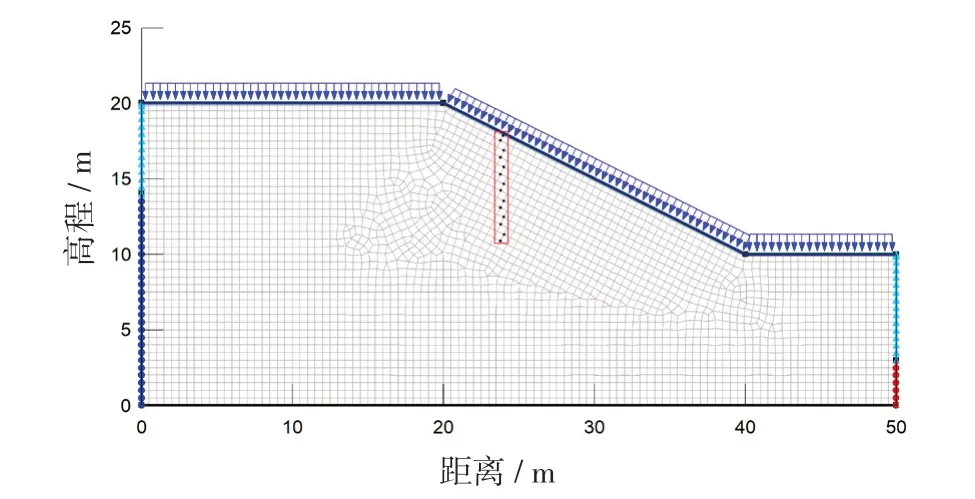
圖2 計算模型

Kitamura等[11]為了探討非飽和土邊坡在降雨外力作用下的邊坡機制，用Shirasu土（日本一種典型土）作為試料，進行了大量的不同類型邊坡模型試驗研究。本研究選取Shirasu土進行邊坡數值分析。土體材料參數見表1。

表1 Shirasu土的材料參數

3.2 邊界條件及SWCC

降雨邊界見圖2，選取3組降雨強度（44 mm/d、110 mm/d和220 mm/d）分別計算降雨持續100 h的邊坡穩定性。根據Milatz等[12]，將3種降雨強度轉換為飽和度變化率（單位均為s-1）數值分別為7.29×10-5、1.82×10-4和3.65×10-4。式（7）中值范圍為30～50 000 kPa·s[6]，由于缺少試驗數據，假設一個中間值10 000 kPa·s來計算率相關SWCC。

利用式（6）和式（7）可對實驗數據[11]進行擬合，所得的SWCC如圖3所示，計算得到的是滲透系數與吸力關系見圖4。可以看出，如果不考慮SWCC率效應，其SWCC和滲透系數曲線都與降雨強度無關，即圖中的率無關曲線。但實際上率效應的存在會明顯改變土體的水力參數，不同降雨強度時，SWCC及滲透系數都發生了變化，這種變化必將影響土體力學特性。

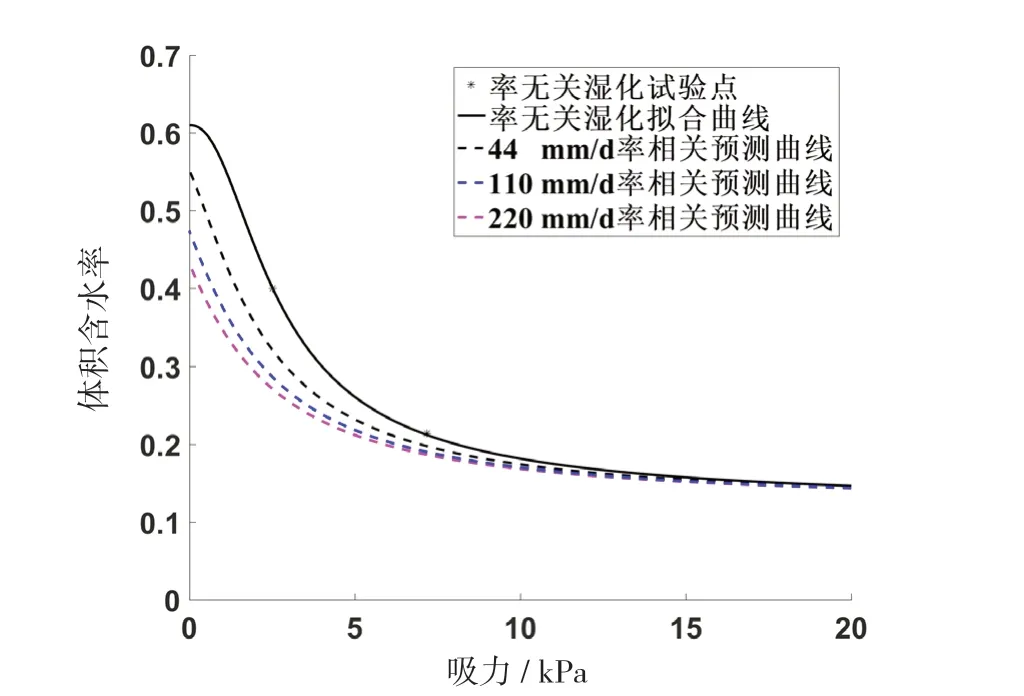
圖3 Shirasu土的SWCC

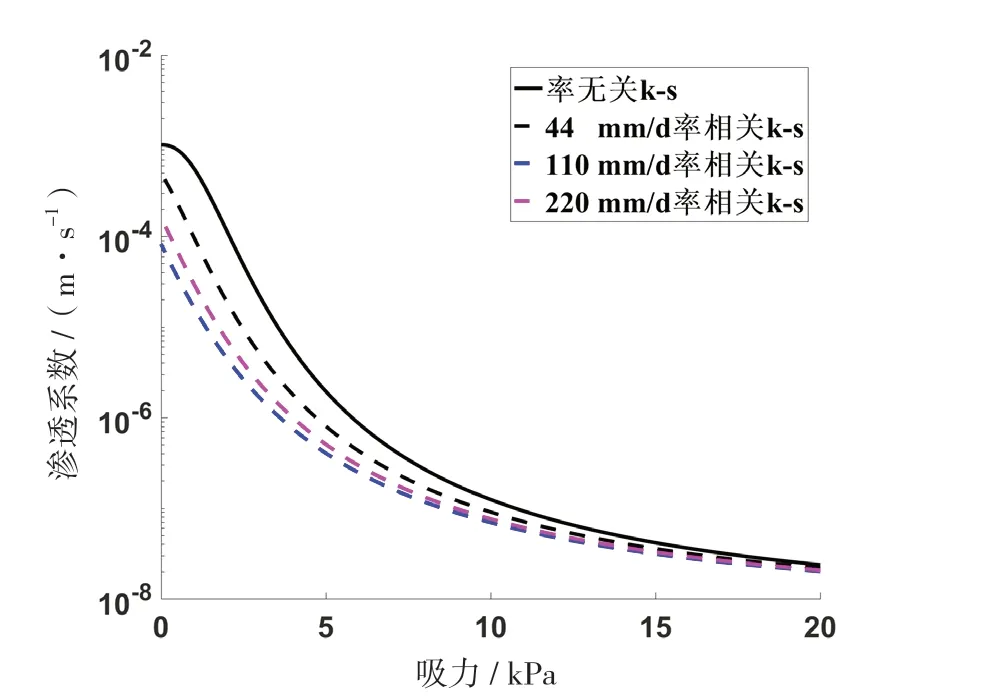
圖4 Shirasu土滲透系數與吸力的關系

3.3 計算步驟

利用Geo-studio軟件進行降雨入滲條件下的邊坡安全分析需要用到SEEP/W和SLOPE/W兩個模塊。

（1）首先利用SEEP/W進行穩態滲流計算，采用圖3和圖4所示的四種土體SWCC曲線和滲透系數曲線。初始邊界為左右兩側的水位和水位上部的不透水邊界。對邊坡左側、右側分別施加14 m、3 m的水頭，并在水位上部施加不透水邊界，進行穩態滲流計算。

（2）確定計算工況。根據是否考慮率相關及降雨強度，共得到6種工況。

表2 工況表

（3）利用SLOPE/W中的極限平衡法進行邊坡穩定性分析，計算各工況邊坡安全系數。

3.4 計算結果

3.4.1 孔隙水壓力結果

提取不同深度的節點數據進行繪圖分析，節點位置見圖2，從坡面往下為A～N。圖5給出了三種降雨強度下，不同深度的孔隙水壓力變化情況，可知，降雨持續時間越長，土體內的孔隙水壓力變化越大；44 mm/d降雨強度下，8 h和24 h時率相關和率無關孔隙水壓力無明顯差別，但隨著降雨持續時間的增加，48 h時，率相關和率無關孔隙水壓力有了較小差別，100 h時，率相關的孔隙水壓力變化明顯大于率無關的孔隙水壓力變化；而在110 mm/d降雨強度下，降雨持續時間為24 h時率相關和率無關孔隙水壓力即有了較小差別，48 h時有明顯差別；220 mm/d降雨強度下，降雨持續時間為8 h時率相關和率無關孔隙水壓力即有較小差別，24 h時就有明顯差別。說明率相關條件下計算所得孔隙水壓力變化比率無關條件下計算孔隙水壓力變化快，而降雨強度越大，其變化越快，且其差別也越明顯。

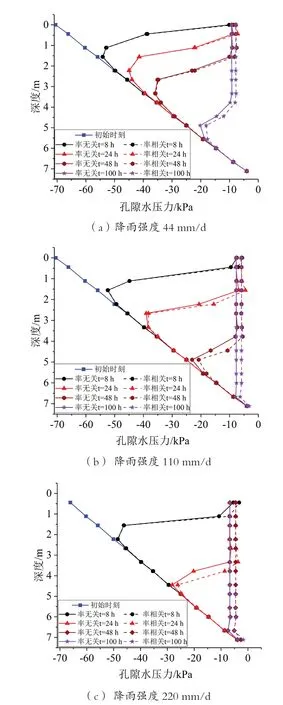
圖5 不同降雨強度下孔隙水壓力隨深度的變化

3.4.2 安全系數對比

圖6給出了不同降雨持續時間下安全系數變化。初始時刻，各工況的安全系數相同。三種降雨強度下，率相關和率無關條件下安全系數均隨降雨持續時間的增加降低，當降雨持續一定時間后，邊坡安全系數將趨于穩定，降雨強度越大，穩定需要的時間越短。三種降雨強度下，率相關條件下計算的安全系數小于率無關條件下計算的安全系數，降雨前期差別較小，隨著降雨持續時間的增加，安全系數差別越來越大。因此，當計算非飽和土邊坡安全系數時，應考慮率效應帶來的影響。

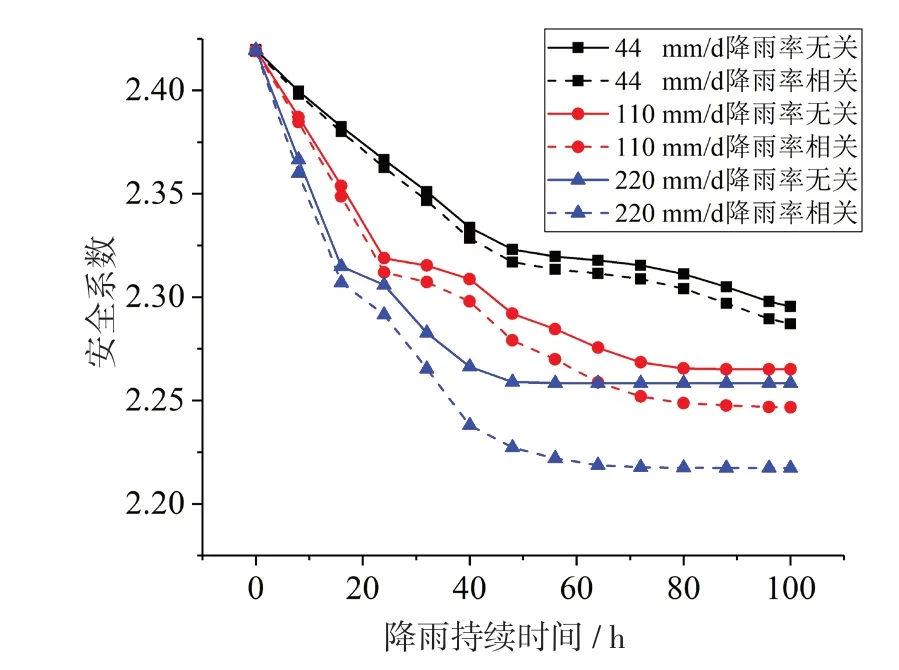
圖6 不同降雨強度下安全系數變化圖

4 結論

首先介紹了率相關SWCC模型，給出了率效應影響的非飽和土滲流模型并將其引入抗剪強度準則，推導得到了基于率相關SWCC的邊坡安全系數公式。采用Geo-Studio軟件計算了不同工況下的邊坡安全系數。主要結論如下：

（1）在各種工況下計算得到的安全系數，均隨著降雨強度的增大而降低。當降雨持續一定時間后，邊坡安全系數將趨于穩定。三種降雨強度下，率相關條件下計算的安全系數均小于率無關條件下的安全系數，隨著降雨持續時間的增加，其安全系數差別越來越大。說明利用率相關SWCC計算的安全系數和利用率無關計算的安全系數有很大差異，實際應用中需根據降雨強度和降雨持續時間進行具體計算分析。

（2）雖然兩種情況下計算所得的安全系數都是隨著降雨強度的增大而降低，但是利用率相關SWCC計算的結果變化幅度更大。利用率相關SWCC計算的安全系數更易受到降雨強度的影響。