時滯反饋下分數階Rayleigh系統的穩定性分析
陳聚峰, 申永軍, 張 靜, 李向紅, 王曉娜
(1. 石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室,石家莊 050043; 2. 石家莊鐵道大學 數理系,石家莊 050043; 3. 石家莊鐵道大學 機械工程學院,石家莊 050043; 4. 石家莊郵電職業技術學院 基礎部,石家莊 050021; 5. 河北軌道運輸職業技術學院 機電工程系,石家莊 050021)
自1927年荷蘭物理學家van der Pol等[1]在描述真空管電路時建立了van der Pol方程后,van der Pol型振子作為一種典型的含有非線性阻尼的自激振動系統,得到了學者們的廣泛關注和深入研究[2-5]。Rayleigh振子屬于van der Pol型振子,并且具有相似的動力學特性,它與van der Pol振子的區別是:隨著電壓的增加,van der Pol振子的頻率增加,而Rayleigh振子的振幅增加。在不同領域,Rayleigh振子可以用來描述許多自激振蕩系統。比如,在土木工程中Rayleigh振子可用于描述安裝在非線性阻尼彈性支承上的梁的模態動力學以及梁在風激勵下的動力學模型[6-7]。受驅動的Rayleigh振子可以用來描述地震的動力學[8]。通過試驗和理論研究表明,Rayleigh振子還可用于驅動柔性機械臂[9-10]。
分數階微積分是應用數學的一個重要分支,它是將整數階微積分推廣至任意實數階甚至復數階的微積分理論[11-13]。現實世界中許多物體運動都可以用分數階模型來識別和描述,與整數階模型相比,其優點是:分數階導數在描述各種過程的記憶和遺傳特性方面具有優異的性能。近年來,隨著計算機技術的加速發展,分數階微積分在諸如物理、工程、經濟學、生物學、材料科學等各個領域的應用受到了廣泛的關注[14-21]。同時,許多不同類型的分數階van der Pol/Rayleigh振子也越來越受到關注[22-25]。例如:Shen等[26]利用平均法研究了含有分數階導數的van der Pol 振子發生主共振的動力學特性;Zhang等[27-28]利用Melnikov方法研究了分數階Rayleigh-Duffing的混沌及同步;Zhang等[29]利用隨機平均法研究了在高斯白噪聲激勵下含有分數階導數的Duffing-Rayleigh系統的響應;Xiao等[30]研究了狀態反饋下一類分數階van der Pol系統的穩定性和Hopf分岔控制。另外,在控制系統中不可避免地存在時滯現象,一方面,時滯的存在往往會導致系統失穩以及控制性能下降;另一方面,人們可以利用時滯進行控制設計來改善系統的穩定性[31-33]。目前,對于時滯反饋下分數階Rayleigh系統的穩定性方面的研究還很少。因此,本文以時滯作為分岔參數,討論一類分數階Rayleigh系統在時滯速度反饋下的穩定性及分岔問題。
1 時滯反饋下分數階Rayleigh系統的穩定性分析
考慮在速度時滯反饋控制下,同階次的分數階Rayleigh系統
(1)
式中: 0
式中,Γ(y)為Gamma函數,且Γ(y+1)=yΓ(y)。
式(1)有唯一平衡點(x1,x2)=(0,0),相應的線性化系統為
(2)
特征方程為

(3)
利用Tavazoei等的方法,我們可得:
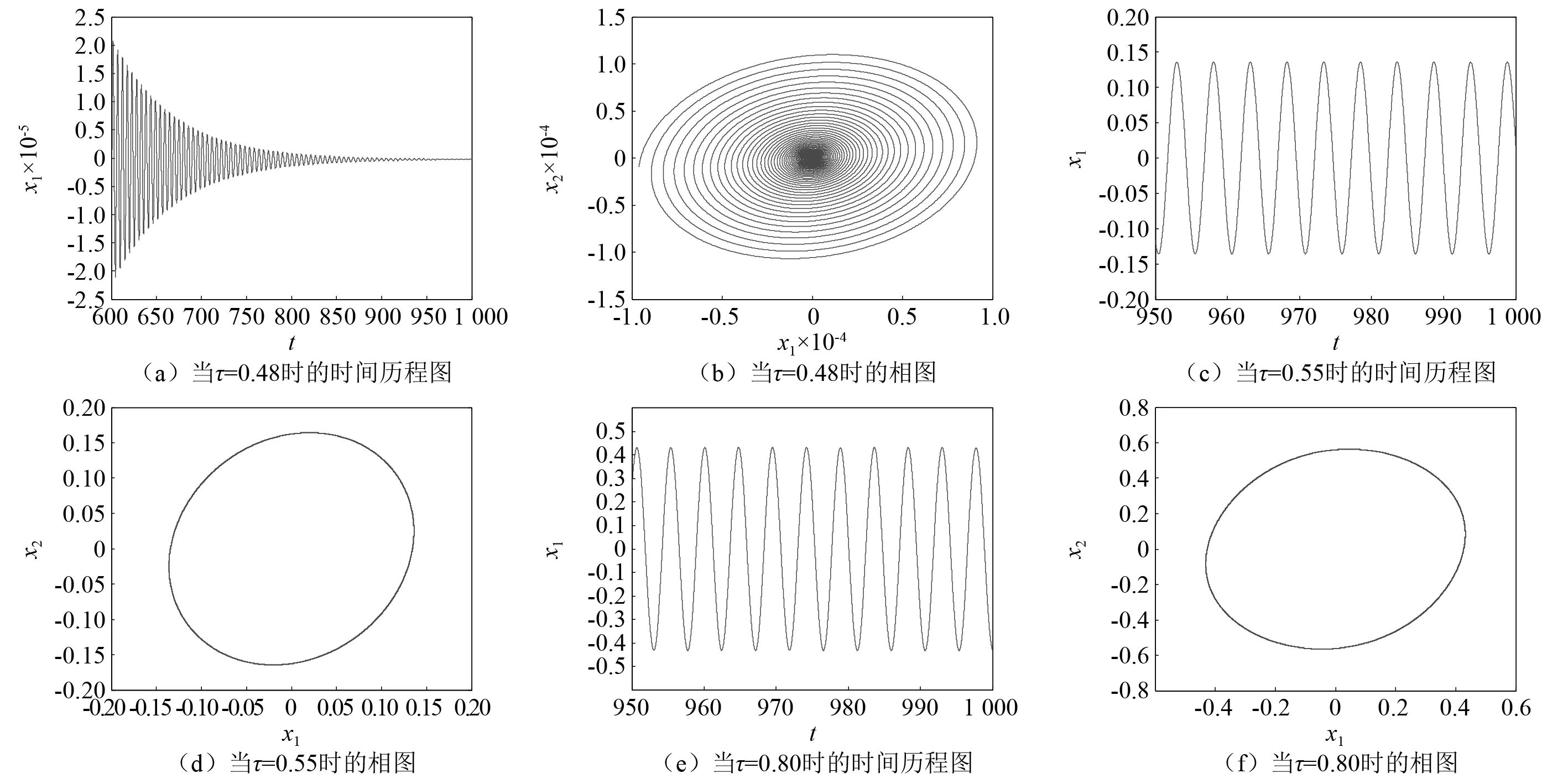
定理1當τ=0時,對每一固定的q,式(1)的平衡點(0,0)是漸近穩定的充要條件為0 (4) 可見,系統參數a的臨界值ac不僅與反饋增益k有關,還與分數階階次q有關。隨著q的減小,k的增大,系統平衡點漸近穩定的參數a的范圍會增大。 接下來,將討論對任意的τ>0,特征方程det[Δ(s)]=0沒有純虛根的條件。 (5) 分離實部和虛部,可得 A1cosωτ+A2sinωτ=δ1 (6) A2cosωτ-A1sinωτ=δ2 (7) 其中, (8) (9) (10) 式(6)和式(7)兩邊平方相加后,可得 ω4q+b3ω3q+b2ω2q+b1ωq+1=0 (11) 其中, 令ωq=z,則式(11)變為 z4+b3z3+b2z2+b1z+1=0 (12) 記H(z)=z4+b3z3+b2z2+b1z+1,則有 H′(z)=4z3+3b3z2+2b2z+b1 令 4z3+3b3z2+2b2z+b1=0 (13) y3+p1y+q1=0 (14) 由Cardano公式,可得式(14)的根為 引理1[34]若Δ≥0,則式(12)有正根當且僅當z1>0及H(z1)<0;若Δ<0,則式(12)有正根當且僅當至少存在一個z*∈{z1,z2,z3},使z*>0及H(z*)≤0。 令 (15) 因此,可定義 (16) 引理2考慮如下的指數多項式 引理3假定0 (ⅰ) 若下列兩個條件之一成立: (a) Δ≥0,z1>0且H(z1)<0; (b) Δ<0,且存在一個z*∈{z1,z2,z3},使z*>0和H(z*)≤0。 則當τ∈[0,τ0)時,式(3)的所有根都具有負實部。 (ⅱ) 若(ⅰ)中兩個條件都不滿足,則對于任意的τ≥0,式(3)的所有根都具有負實部。 證明當τ=0,由定理1可知,當0 令 s(τ)=α(τ)+iω(τ) (17) 是式(3)滿足α(τ0)=0,ω(τ0)=ω0的根。 證明式(3)兩邊關于τ求導,得 (18) 于是, (19) 因此,當τ=τ0,s=iω0,式(19)變為 (20) 其中, 所以, 因此, 從而結論成立。 由引理1、引理3及引理4,我們可得: 定理2令ω0,z0,τ0及s(τ)是由式(16)和式(17)所定義,假定0 (ⅰ) 若下面兩個條件: (a) Δ≥0,z1>0且H(z1)<0; (b) Δ<0,且存在一個z*∈{z1,z2,z3},使z*>0和H(z*)≤0。 都不滿足,則對于任意的τ≥0,式(1)的零解是漸近穩定的。 (ⅱ) 若滿足(ⅰ)中條件(a)和條件(b)之一,則當τ∈[0,τ0)時,式(1)的零解是漸近穩定的。 本章將選取三組系統參數,分別對分數階Rayleigh系統進行數值仿真,以驗證理論結果的正確性。這里我們采用G-L定義法對其數值解進行模擬。 取時滯τ=0.48<τ0,則式(1)的零解是漸近穩定的,如圖1(a)和圖1(b)所示;再取時滯τ=0.55>τ0,則式(1)的零解是不穩定的,出現了周期解,如圖1(c)和圖1(d)所示;最后取時滯τ=0.80>τ2>τ0,則式(1)的零解仍是不穩定的,系統存在周期解,如圖1(e)和圖1(f)所示。因此,式(1)在τ=τ0處發生Hopf分岔。這與定理2的結論完全相符。 圖1 當q=0.9,k=0.6時,式(1)的時間歷程圖和相圖Fig.1 Time histories and phase diagrams of Eq.(1) with q=0.9 and k=0.6 取時滯τ=0.275<τ0,則式(1)的零解是漸近穩定的,如圖2(a)和圖2(b)所示;再取時滯τ=0.315>τ0,則式(1)的零解是不穩定的,出現了周期解,如圖2(c)和圖2(d)所示;最后取時滯τ=0.600>τ2>τ0,則式(1)的零解仍是不穩定的,系統存在周期解,如圖2(e)和圖2(f)所示。因此,式(1)在τ=τ0處發生Hopf分岔。 (ⅲ) 選取q=0.9,k=0.05,則由式(4)可得ac=0.362 9。取a=0.2 圖3 當q=0.9,k=0.05時,式(1)的相圖Fig.3 Phase diagrams of Eq.(1) with q=0.9 and k=0.05 本文主要對速度時滯反饋下分數階Rayleigh系統的穩定性和Hopf分岔條件進行分析。以時滯τ作為分岔參數,當τ=0時,分數階Rayleigh系統具有線性反饋,得到了平衡點漸近穩定的充要條件,它不僅與反饋增益k有關,還與分數階階次q有關;當τ>0時,基于特征方程,當系統參數滿足定理2中的條件,可以計算出平衡點穩定的時滯參數臨界值τ0,當時滯參數小于τ0時,平衡點是穩定的,當時滯參數大于τ0時,平衡點是不穩定的;進而,得到Hopf分岔發生的條件。可見,通過調節時滯的參數值,可以控制分數階系統的穩定性與分岔。
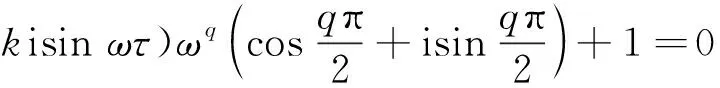

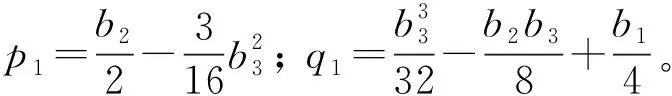
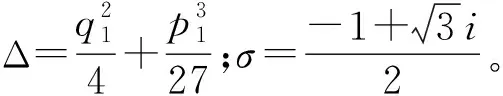

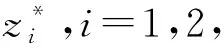
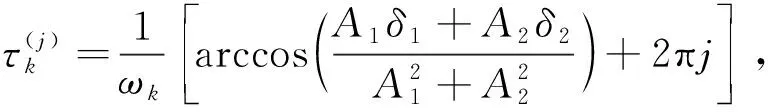

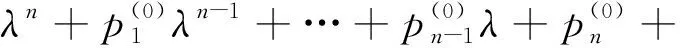
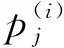
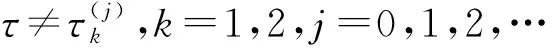



2 數值模擬



3 結 論

