Alford力和中介軸承對雙轉子系統動力學特性的影響

鄭華林， 金洹冰， 王小虎， 李炎軍

(1. 西南石油大學 機電工程學院，成都 610500； 2. 中國航發四川燃氣渦輪研究院，成都 610500)

轉子系統是旋轉機械的核心，在各個領域都有著廣泛的應用，例如在現代航空發動機中，為了提高推重比，減少整機質量，往往會使用雙轉子系統。在雙轉子系統中，高壓轉子與低壓轉子通過中介軸承連接。由于中介軸承的存在，整個雙轉子系統振動耦合非常強烈。中介軸承內外圈同時旋轉，潤滑條件較差，極易發生故障[1-3]。因此，對雙轉子-中介軸承系統的動力學特性進行研究具有重要意義。

使用軸流式壓氣機的航空發動機，由于制造或裝配的誤差，葉輪和機匣之間會存在一定的徑向偏離，會使壓氣機葉尖間隙沿周向分布不均勻，在轉子旋轉時，會導致葉片上的氣動力不等，葉片的氣動力除了會合成一個扭矩外，還會合成一個作用于軸心的橫向力[4-6]。1958年，德國的Thomas[7]在對氣體透平的不穩定性研究中第一次提出：存在偏心的渦輪在旋轉時會產生一個垂直于偏心方向的力，將其稱為間隙激勵力。1965年，美國的Alford[8]進一步揭示了間隙激勵力產生的機理，后面習慣將其稱為Alford力。后來的學者對Alford力進行了許多研究。Kim等[9]將細長軸采用Euler-Bernoulli梁理論建模后與風機模型耦合，研究表明Alford力會導致結構不穩定。白長青等[10]研究了Alford力和滾動軸承對軸流壓縮機轉子系統動力學特性和穩定性的影響，研究表明超過臨界轉速，Alford力對轉子系統的穩定性影響會更大。成玫等[11]研究了滾動軸承和轉子Alford力的影響后，發現滾動軸承間隙對系統穩定性影響較大。王小虎等[12]研究了磁懸浮軸承和Alford力的影響，建立了系統的有限元模型，結果表明，在非線性Alford力和磁軸承電磁力共同作用下，轉子系統表現出了較復雜的動力學特征。上述研究結果表明，Alford力對轉子系統的穩定性有很大的影響。在航空發動機雙轉子系統中，由于存在中介軸承力，再加上轉子運動時產生的Alford力，使得整個系統運動極為復雜。目前關于Alford力對雙轉子系統動力學特性影響的研究較少，因此，為了解航空發動機雙轉子系統在實際運行過程中的情況，研究中介軸承力和Alford力共同作用下雙轉子系統的動力學特性非常有必要。

以航空發動機典型雙轉子系統為研究對象，考慮中介軸承非線性接觸力，考慮壓氣機盤上的Alford力，采用Euler-Bernoulli梁理論建立了雙轉子系統的動力學模型，利用有限單元法和Newmark-β法求解出系統的響應，結合頻譜圖、軸心軌跡圖、龐加萊截面圖對系統進行分析。

1 系統建模

1.1 雙轉子系統建模

所研究的雙轉子系統結構簡圖[13]如圖1所示，將系統離散為若干軸段、剛性圓盤以及支承單元。軸段采用Euler-Bernoulli梁理論進行建模；圓盤考慮為剛性體；每個節點有4個自由度，包括2個平動和2個轉動，該模型8個節點共有32個自由度；支承軸承等效為彈簧阻尼結構。

圖1 雙轉子系統簡化模型Fig.1 Simplified model of dual-rotor system

圓盤的廣義坐標就是其軸心節點的位移向量，包括沿x軸的平動和轉動，以及沿y軸的平動和轉動，其節點的質量矩陣Md和陀螺矩陣Gd可表示為

(1)

(2)

式中：m為圓盤的質量；Jd為圓盤過軸心的直徑轉動慣量；Jp為圓盤過軸心的極轉動慣量；在陀螺矩陣中，ω為轉速，對于本文所研究的雙轉子系統，在計算時需要分別代入高壓轉子轉速ωH和低壓轉子轉速ωL。

對于彈性軸段單元，其廣義坐標是兩端節點的位移向量,其節點的移動慣性矩陣MT、轉動慣性矩陣MR、陀螺矩陣Gb、剛度矩陣Kb[14]均可分別表示為

(3)

(4)

(5)

(6)

節點的質量矩陣為移動慣性矩陣與轉動慣性矩陣之和，即

Mb=MT+MR

(7)

式中：ρ為軸段密度；A為軸段橫截面積；l為軸段長度；R和r分別為軸段內外半徑；E為彈性模量；I為截面慣性矩；在陀螺矩陣中，ω為轉速，對于本文所研究的雙轉子系統，在計算時需要分別代入高壓轉子轉速ωH和低壓轉子轉速ωL。

將低壓軸段的單元矩陣與低壓軸上圓盤的單元矩陣按照自由度相對應的原則進行組裝，即可得到低壓軸的質量矩陣、剛度矩陣和陀螺矩陣。同理可以得到高壓軸的質量矩陣、剛度矩陣和陀螺矩陣。

在圖1所示靜坐標系XYZ下，低壓軸的運動方程可以表示為

(8)

式中：ML為低壓軸質量矩陣；CL為低壓軸阻尼矩陣，以瑞利阻尼的形式引入；GL為低壓軸陀螺矩陣；KL為低壓軸剛度矩陣；u1L和u2L分別為低壓軸x自由度和y自由度的位移向量；F1L和F2L為低壓軸廣義力向量。

同理，高壓軸的運動方程可以表示為

(9)

式中：MH為高壓軸質量矩陣；CH為高壓軸阻尼矩陣，以瑞利阻尼的形式引入；GH為高壓軸陀螺矩陣；KH為高壓軸剛度矩陣；u1H和u2H分別為高壓軸x自由度和y自由度的位移向量；F1H和F2H為高壓軸廣義力向量。

聯立式(8)和式(9)，可以得到運動方程的矩陣形式。將與機匣相連的3個支承軸承剛度和阻尼加入到系統中。按照等剛度彈性支承[15]將剛度系數加入系統剛度矩陣相應自由度，對于支承軸承的阻尼系數也可以按照剛度系數疊加的方法疊加到系統阻尼矩陣中。

由此可以得到系統的運動學方程為

(10)

式中：M為整個系統的慣性矩陣(含輪盤轉動慣量)；C為系統阻尼矩陣；G為陀螺矩陣(含輪盤)；K為系統剛度矩陣；u為廣義坐標向量；F為轉子系統的廣義力向量。

1.2 中介軸承力建模

在如圖2所示簡化中介軸承動力學模型中[16]：ωo，ωi分別為中介軸承外圈轉速和內圈轉速；θj為第j個滾子在任意時刻的瞬時角位置。

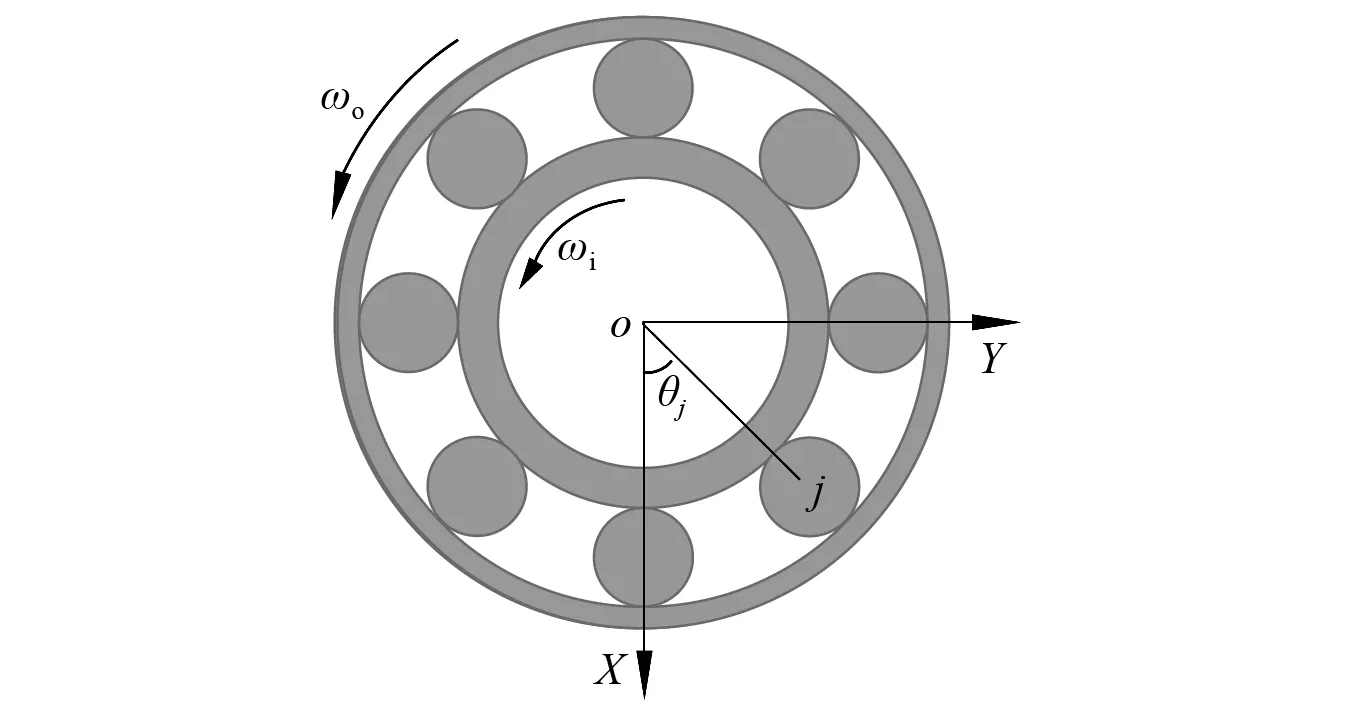
圖2 中介軸承簡化模型Fig.2 Simplified model of inter-shaft bearing

假設滾子在內外圈之間作純滾動，保持架的轉速可以表示為

(11)

任意時刻，第j個滾子的瞬時角位置可以表示為

(12)

式中:θ0為第1個滾子相對于x軸的初始夾角；Nb為滾子個數。

假設系統發生小變形，第j個滾子與中介軸承內外圈接觸時總的變形量為

δj=(xi-xo)cosθj+(yi-yo)sinθj-δ0

(13)

式中：xi，xo，yi，yo分別為中介軸承內圈在x方向的位移分量、外圈在x方向的位移分量、內圈在y方向的位移分量、外圈在y方向的位移分量；δ0為軸承的徑向游隙。

根據赫茲接觸理論[17]，非線性接觸力可以表示為

(14)

因此，每個滾子在x方向和y方向上Hertz接觸力的投影之和，即為中介軸承總體的Hertz接觸力在x方向和y方向上的分量，可以表示為

(15)

1.3 Alford力建模

航空發動機轉子受重力產生靜態變形，運行過程中受不平衡力等動態激勵力而產生徑向振動，靜態變形和徑向振動會使葉輪在徑向產生偏心。葉輪偏心會導致周向葉尖間隙不等，葉片上圓周方向的力不僅會合成一個扭矩，還會產生一個作用于軸心的橫向力，這一橫向力就被稱為Alford力，如圖3中FA。

圖3 Alford力模型Fig.3 The model of Alford force

Thomas和Alford兩人均提出了Alford力的計算公式，Thomas建立的公式中dξ/dδ難以確定，Alford建立的公式效率系數β會隨著不同的葉輪結構而發生改變，不是一個固定的值，因此Thomas和Alford兩人建立的Alford力的計算公式只適用于定性分析。柴山等[18]從流體力學出發，對原始Alford力計算表達式進行了改進，得到新的Alford力公式，表示為

(16)

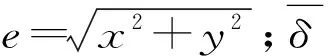
得到Alford力后，轉子坐標系nO′t與XOY不重合，因此可以將FA在x方向和y進行分解，就可以得到Alford力在x方向和y方向的分量。

2 仿真結果與分析

該模型有8個節點，共32個自由度，采用Newmark-β法對該系統的32維動力學方程進行求解，時間步長為1×10-5s。不平衡力分別施加在高壓和低壓渦輪盤對應節點上，其中高壓不平衡量和低壓不平衡量分別為0.5 μm和1.0 μm；中介軸承力施加在中介軸承對應節點上；Alford力施加在低壓壓氣盤對應節點上；整個系統都受到了重力的作用，因此在每個節點的x自由度上以加速度的形式施加重力；高低壓轉子轉速比λ=1.2。雙轉子系統參數如表1所示。

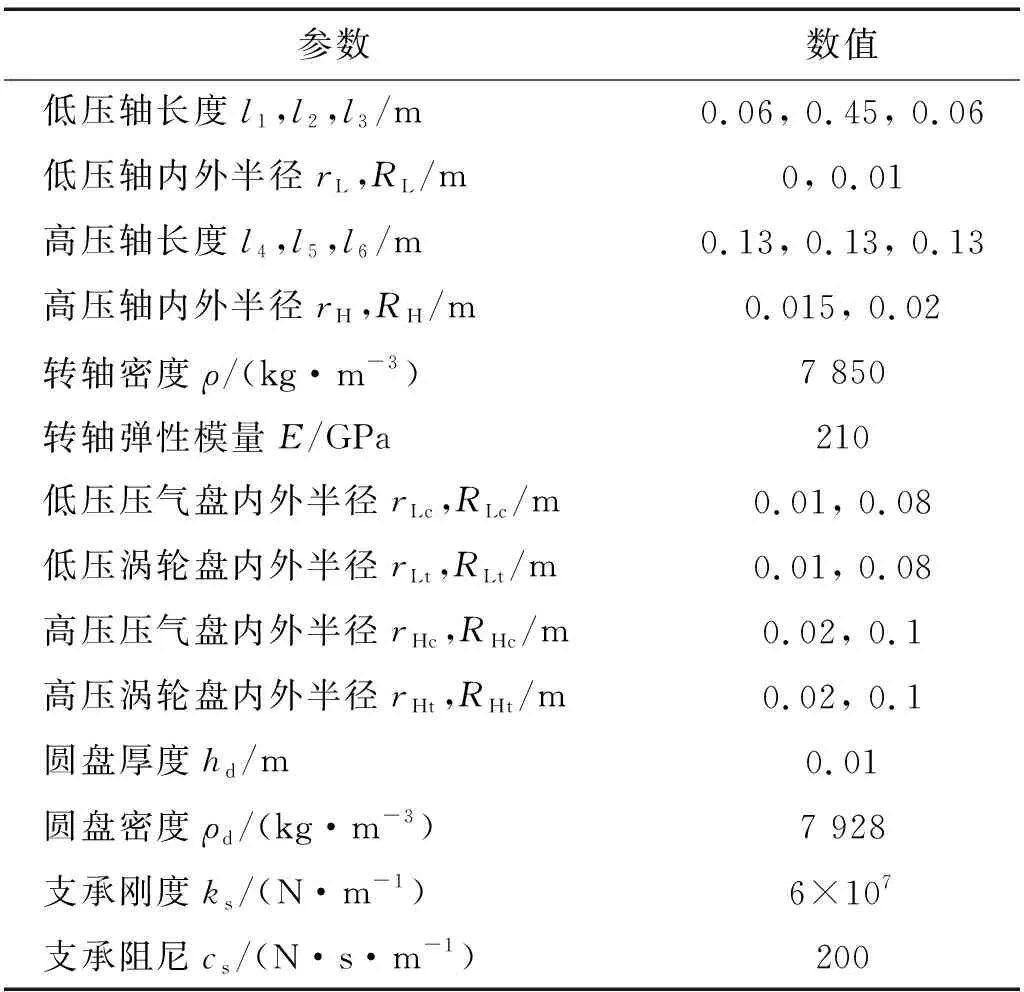
表1 雙轉子系統參數Tab.1 Model parameters of the dual-rotor system

中介軸承模型參數

ro=15 mm,ri=10 mm,Nb=8,Kb=3×109N/m10/9。

Alford力模型參數

2.1 Alford力對系統的影響

利用本文模型和計算方法，通過計算系統的升速響應，獲得了雙轉子系統在不同工況下的臨界轉速列于表2和表3中。從表2可以看出，不考慮Alford力時，內轉子同步渦動引起的一階臨界轉速為122 rad/s，二階臨界轉速為145 rad/s，外轉子同步渦動引起的一階臨界轉速為84 rad/s，二階臨界轉速為97 rad/s；從表3可以看出，考慮Alford力時，內轉子同步渦動引起的一階臨界轉速為132 rad/s，二階臨界轉速為192 rad/s，外轉子同步渦動引起的一階臨界轉速為91 rad/s，二階臨界轉速為131 rad/s。對比表2和表3可以發現，Alford力的引入會導致內轉子同步渦動和外轉子同步渦動引起的臨界轉速均有所提高。

表2 無Alford力時的臨界轉速Tab.2 Critical speed without Alford force 單位：rad/s

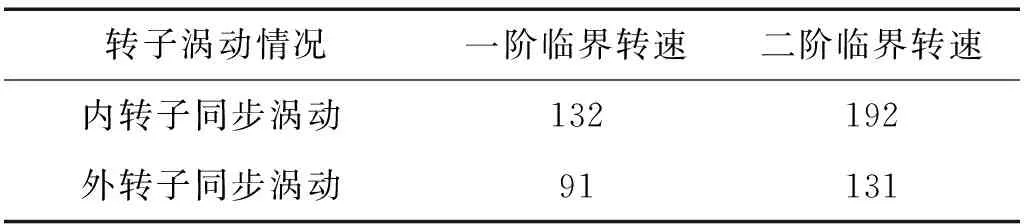
表3 有Alford力時的臨界轉速Tab.3 Critical speed with Alford force 單位：rad/s

圖4和圖5分別繪制了有無Alford力的振動響應。頻譜圖中，fl，fh，fvc分別為低壓轉子轉頻、高壓轉子轉頻和中介軸承滾子通過頻率。對比圖4(a)和圖5(a)，不考慮Alford力時，頻譜圖中出現低壓轉子轉頻以及中介軸承滾子通過頻率，龐加萊截面圖為封閉的心形，系統作擬周期運動；考慮Alford力時，除出現上述頻率外，還出現了更多的中介軸承特征頻率以及一系列的連續頻率，龐加萊截面為一個封閉的圖形，系統作擬周期運動。對比圖4(b)和圖5(b)，不考慮Alford力時，頻譜圖中高低壓轉子轉頻非常明顯，龐加萊截面為5個孤立的點，系統作五周期運動；考慮Alford力時，頻譜圖中不僅出現了高低壓轉子轉頻，還出現了中介軸承特征頻率以及中介軸承特征頻率和轉子轉頻的組合頻率，龐加萊截面為封閉的圖形，系統作擬周期運動。對比圖4(c)和圖5(c)，不考慮Alford力時，頻譜圖中同樣也是高低壓轉子轉頻很明顯，龐加萊截面為2個封閉圖形，系統作擬周期運動；考慮Alford力時，頻譜圖中還出現了中介軸承特征頻率、組合頻率以及連續頻率，龐加萊截面為一片云狀圖，系統作混沌運動。

圖4 無Alford力時的振動響應Fig.4 Vibration response without Alford force

圖5 有Alford力時的振動響應Fig.5 Vibration response with Alford force

綜上所述，Alford力會導致系統動力學行為發生改變，系統會從周期運動進入擬周期運動，甚至會進入混沌。Alford力極易激發中介軸承力的非線性特性，導致系統的運動更加復雜。從頻譜圖的對比可以看出，Alford力引入系統后，會以組合頻率和連續頻率的形式影響系統的運動。同時，對比有無Alford力的頻譜幅值可以發現，Alford力的引入反而會使振動的幅值減小，原因可能是作用于橫向的Alford力對橫向振動有抑制作用，從而振幅會減小。從圖4和圖5可以看出，不同轉速和中介軸承游隙下，Alford力對系統的作用效果也不盡相同，2.2節和2.3節將詳細分析不同轉速和游隙下的振動特性。

由上述研究可知，Alford力極易激發中介軸承力的非線性特性，為探究其原因，從計算結果中提取了中介軸承力計算時的主要參數，即滾子變形量，從中介軸承力建模過程可知，當滾子變形量大于0時滾子才與滾道有接觸從而產生接觸力。圖6繪制了不考慮Alford力和考慮Alford力時某一滾子的變形量曲線，對比兩條曲線可以發現，有Alford力時變形量曲線位于無Alford力時變形量曲線的上方，同時可以發現有Alford力時滾子變形量大于0的時間更長，表明滾子與滾道接觸時間更長。由此可知，Alford力會通過影響中介軸承滾子與滾道的接觸行為來影響中介軸承力。

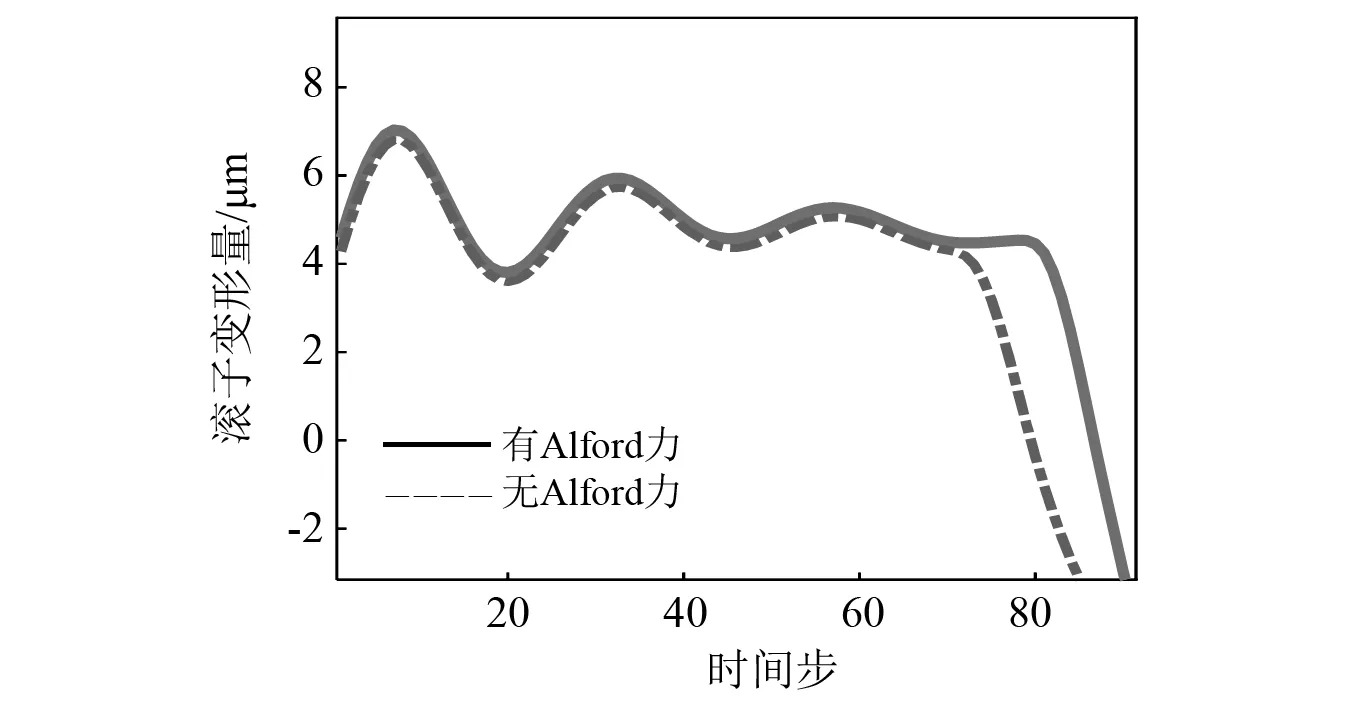
圖6 滾子變形量Fig.6 Roller deformation

2.2 轉子轉速的影響

轉子轉速對系統的動力學特性有顯著的影響，圖7～圖9是在中介軸承力和Alford力共同作用下，中介軸承游隙為1 μm，低壓轉子轉速分別為200 rad/s，400 rad/s和600 rad/s情況下進行數值計算的結果。

隨著轉速升高，軸心軌跡由細長的心形變為長軸沿縱向較為混亂發散的橢圓形，接著變成混亂的花瓣狀(見圖7(a)、圖8(a)、圖9(a))；龐加萊截面圖由一個封閉的心形變為一個封閉的近似圓形，最后變為一片云狀的散點，系統經歷了從擬周期到擬周期再到混沌運動的變化(見圖7(b)、圖8(b)、圖9(b))。

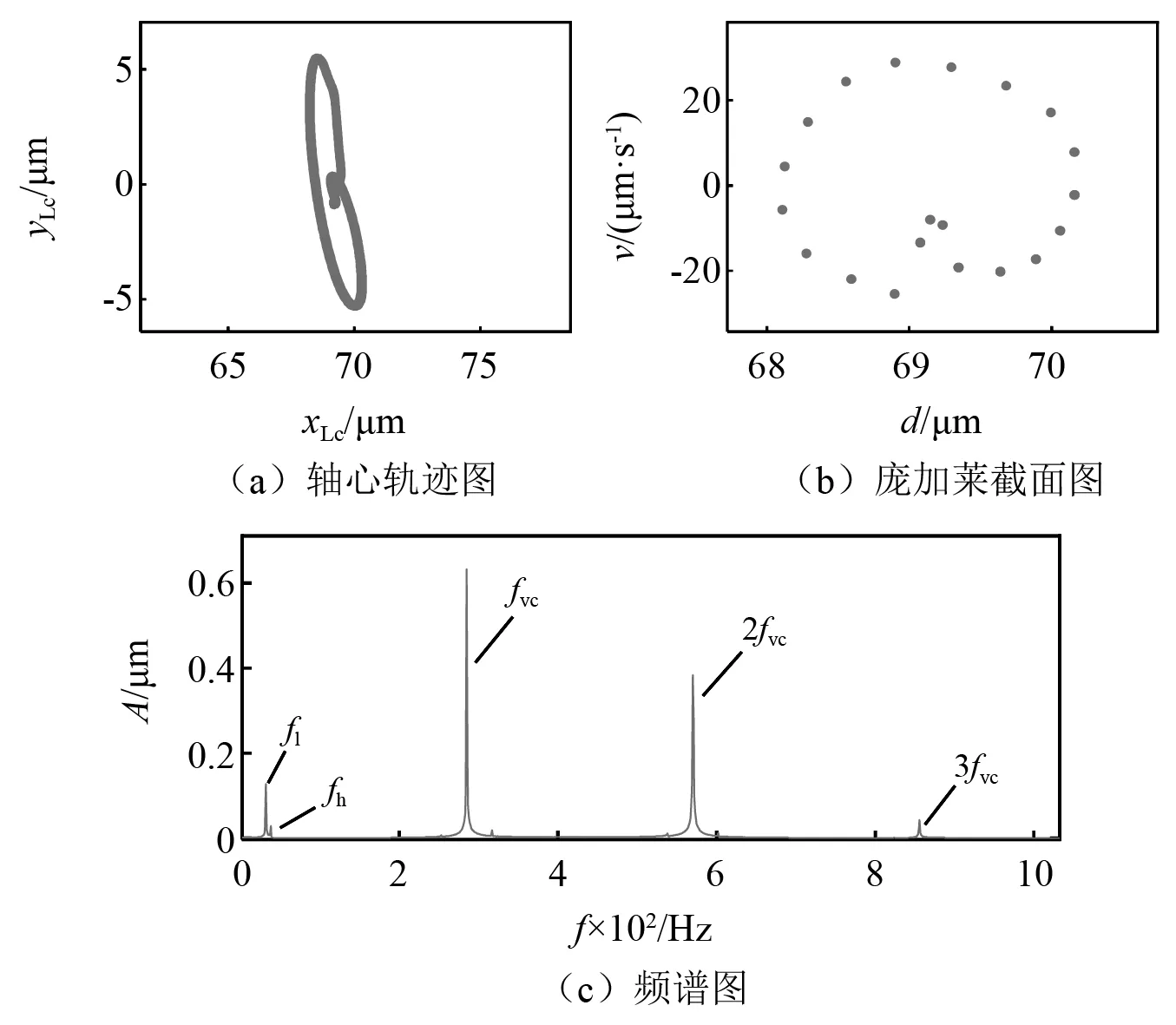
圖7 ωL=200 rad/s時的振動響應Fig.7 Vibration response at ωL=200 rad/s

圖8 ωL=400 rad/s時的振動響應Fig.8 Vibration response at ωL=400 rad/s

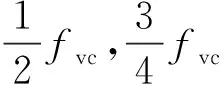
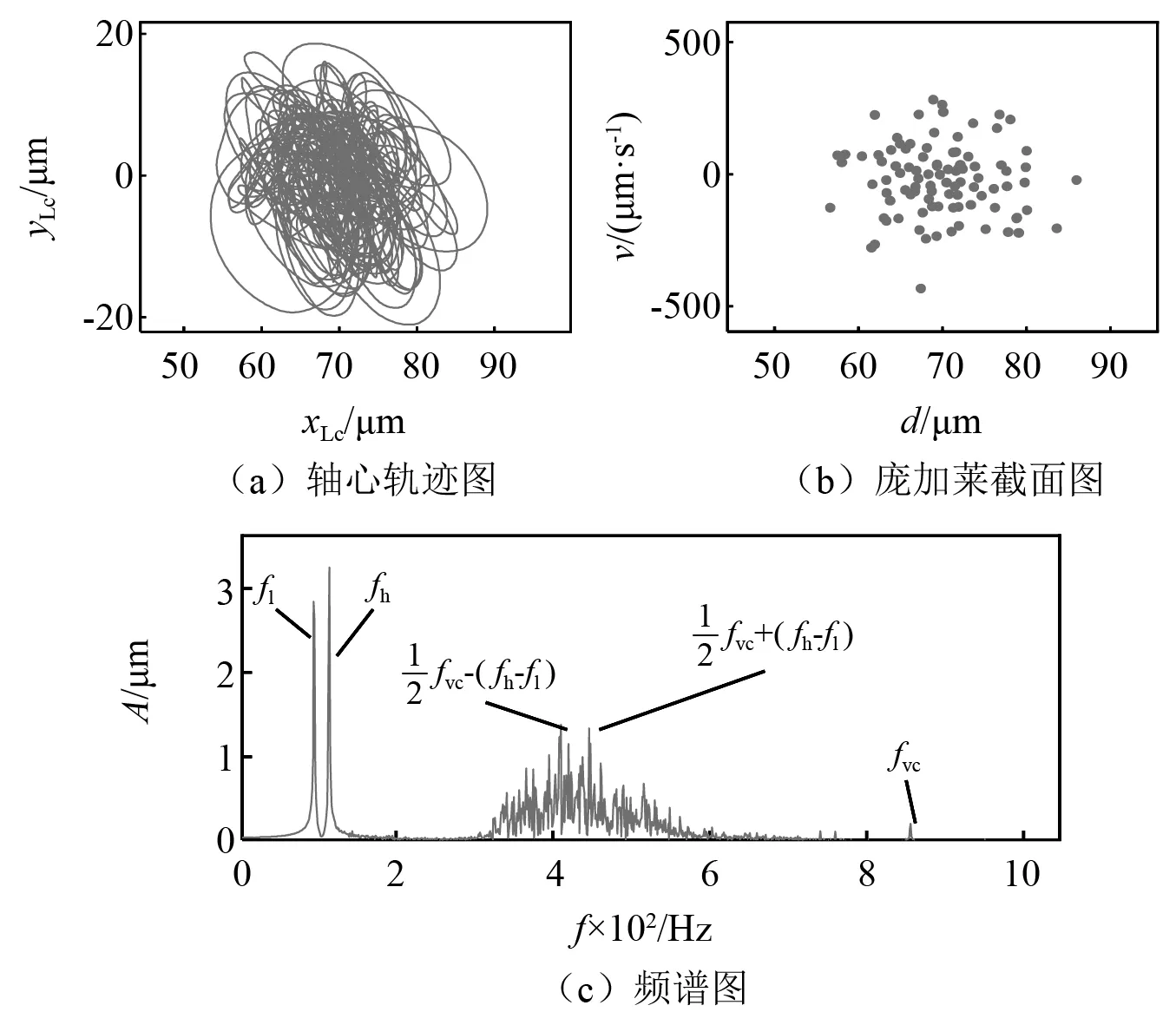
圖9 ωL=600 rad/s時的振動響應Fig.9 Vibration response at ωL=600 rad/s

2.3 中介軸承游隙的影響

在實際運動過程中，中介軸承會產生磨損導致游隙變化，游隙的存在會使系統產生很強的非線性，研究中介軸承游隙的影響有非常重要的意義。圖10～圖12是在中介軸承力和Alford力共同作用下，低壓轉子轉速為1 400 rad/s，中介軸承游隙δ0分別為1 μm，2 μm，5 μm時進行數值計算的結果。

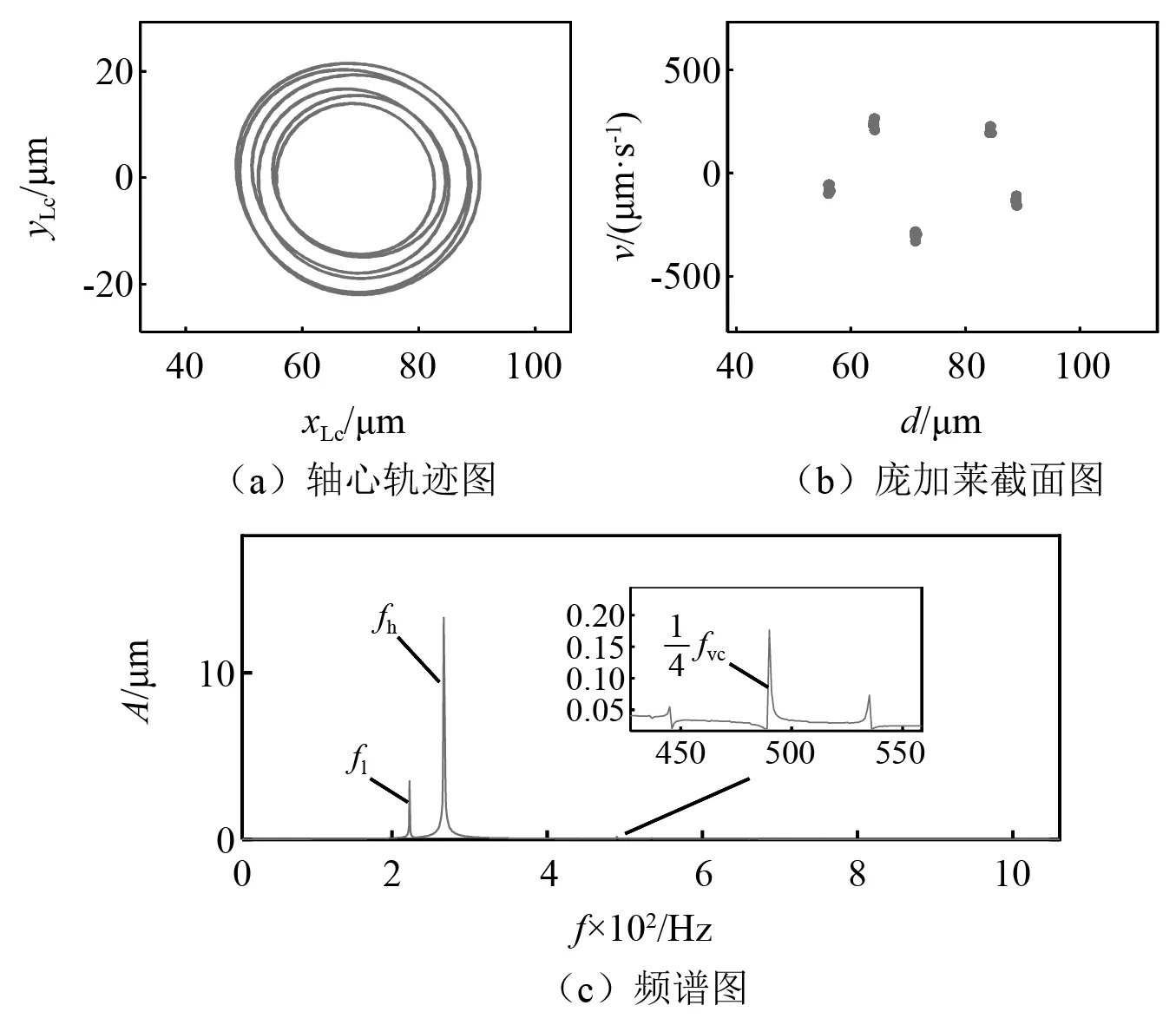
圖10 δ0=1 μm時的振動響應Fig.10 Clearance is δ0=1 μm

圖11 δ0=2 μm時的振動響應Fig.11 Clearance is δ0=2 μm

圖12 δ0=5 μm時的振動響應Fig.12 Clearance is δ0=5 μm

隨著游隙的增大，軸心軌跡由環環相套的圓形變為軌跡交錯混亂的近似三角形，接著軌跡變得雜亂無章(見圖10(a)、圖11(a)、圖12(a))；龐加萊截面由5個點變為一個封閉的圓，最后變成一片散點，系統經歷了從周期運動到擬周期運動再到混沌運動的變化(見圖10(b)、圖11(b)、圖12(b))；當中介軸承游隙為1 μm時(見圖10(c))，頻譜中高壓和低壓轉子轉速對應頻率比較明顯；當游隙增加到2 μm時(見圖11(c))，頻譜圖中除了高壓和低壓轉子轉速對應頻率外，還有部分連續的頻率成分，說明此時Alford力對系統產生了一定的影響；當游隙繼續增加到5 μm時(見圖12(c))，頻譜圖中出現了大量的連續雜亂的頻率成分，Alford力的作用效果更加明顯。

3 結 論

本文對在中介軸承力和Alford力共同作用下的雙轉子系統進行動力學建模，得到系統的動力學方程后，采用Newmark-β法進行數值求解，對系統響應進行分析，得到的具體結論如下：

(1) 引入Alford力后，系統的一階、二階臨界轉速提高，中介軸承的特征頻率極易被激發，Alford力會使中介軸承滾子變形量更大，與滾道接觸時間更長，從而影響中介軸承力，同時由于Alford力的非線性，系統動力學特性會更加復雜，但系統的振幅反而會減小。

(2) 研究轉速對系統運動的影響，發現隨著轉速的增加，中介軸承力的作用效果逐漸減小，而Alford力的作用效果逐漸增加，系統的振幅也會隨轉速增加而變大。

(3) 研究游隙對系統運動的影響，發現游隙的增大會直接引起Alford力的增加，導致系統的不穩定性增強，甚至會導致系統失穩。

因此，雙轉子航空發動機中，中介軸承特性和氣流激勵力共同作用，會極大地改變轉子系統的動力學特性，在設計時應考慮此現象。