冷彎薄壁型鋼組合墻體簡化計算模型研究

管宇 ，周緒紅 ，2，石宇 ，李松松 ，聶少鋒 ，姚欣梅

（1.長安大學 建筑工程學院，陜西 西安 710061；2.山地城鎮建設與新技術教育部重點實驗室（重慶大學），重慶 400045）

在鄉村振興和新型城鎮化發展過程中大力推廣冷彎薄壁型鋼結構體系，符合綠色建筑和裝配式建筑的發展方向，可以提高建設效率、提升建筑品質、降低能耗，符合可持續發展的要求.

組合墻體作為冷彎薄壁型鋼結構體系的主要承重和抗側力構件，由墻架柱、上下導軌及輕質墻板通過自攻螺釘連接而成，其抗側剛度和抗剪承載力主要由冷彎薄壁型鋼骨架與外側輕質墻面板之間的蒙皮效應產生.國內外學者對冷彎薄壁型鋼組合墻體的抗剪性能進行了較為深入的研究.Xu 等［1］提出了冷彎薄壁型鋼組合墻體的抗剪承載力和抗側剛度的理論公式，該公式體現了螺釘間距對墻體抗剪性能的影響.Moghimi 等［2］和Velchev 等［3］通過試驗研究了設置交叉鋼帶支撐的冷彎薄壁型鋼墻體的抗剪性能，指出增強交叉鋼帶與螺釘連接可提高墻體的抗剪性能，增大鋼帶截面可提高墻體的抗側剛度.周緒紅等［4-5］基于冷彎薄壁型鋼組合墻體抗剪試驗結果，提出了考慮剛度退化和捏攏效應的組合墻體退化四線型恢復力模型.Yu 等［6-7］對冷彎薄壁型鋼薄鋼板剪力墻進行了抗震性能試驗研究，破壞特征為鋼板屈曲和螺釘連接破壞，應采用折減系數2w/h（w和h分別為墻體寬度和高度）以考慮高寬比對墻體承載力的影響.Nithyadharan 等［8-9］根據墻體抗剪試驗過程中螺釘經歷的傾斜、承壓和脫開3 個破壞階段，定義了墻體的彈性、屈服和破壞3 個階段，并提出了適用于覆硅酸鈣板組合墻體的滯回模型.Wu等［10］通過抗剪性能試驗對填充輕質材料的冷彎薄壁型鋼組合墻體的受力特性及破壞特征進行了研究分析.袁泉等［11］建立了中間支撐冷彎薄壁型鋼灌漿墻體的有限元模型，通過抗剪性能模擬分析指出Z 形斜撐可有效解決鋼拉條引起的墻體偏心受力問題，顯著提高墻體的抗剪承載力.Xu 等［12-13］對覆秸稈板內填高強輕質泡沫混凝土組合墻體進行了抗震性能研究，采用規范公式計算了該組合墻體的抗剪承載力.Zhang等［14］提出了壓型鋼板蒙皮輕鋼組合墻體的水平側移計算方法.Yu 等［15］通過試驗研究表明壓型鋼板開縫可在保證抗剪承載力較高的同時提高冷彎薄壁型鋼壓型鋼板組合墻體的延性.

現有成果主要集中于墻體抗剪試驗研究和抗剪理論分析，對組合墻體計算模型的研究相對較少.基于此，根據冷彎薄壁型鋼組合墻體的側向變形模式，建立了組合墻體的簡化計算模型，推導了模型中對角彈簧軸向剛度的計算方法.通過冷彎薄壁型鋼組合墻體擬靜力試驗的模擬分析和冷彎薄壁型鋼結構房屋的彈性動力時程分析，驗證了組合墻體簡化計算模型的正確性，并明確了組合墻體簡化計算模型的適用范圍，可為輕鋼結構的抗震設計提供參考.

1 組合墻體簡化計算模型

在水平荷載作用下，冷彎薄壁型鋼組合墻體的側向變形包括剪切變形Δs、彎曲變形Δb和傾倒變形Δr，見圖1.其中，剪切變形為覆面板的剪切變形Δ1與覆面板上螺釘滑移產生的剪切變形Δ2之和；彎曲變形為兩端墻架柱拉、壓產生的變形；傾倒變形為錨栓拔起使墻體轉動所產生的變形，而墻架柱腳的抗拔螺栓可有效抑制墻體發生傾倒，可忽略傾倒變形Δr產生的影響.因此，在水平荷載作用下組合墻體側向變形以剪切變形和彎曲變形為主.

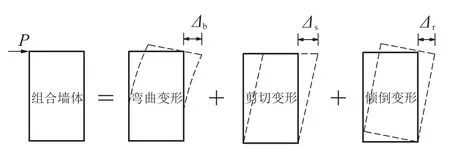
圖1 組合墻體的變形示意圖Fig.1 Deformation diagram of composite wall

組合墻體僅發生剪切變形的簡化計算模型見圖2，其中上導軌和兩側墻架柱忽略彎曲變形的影響，采用桁架桿件進行分析，桿件間采用鉸接約束.

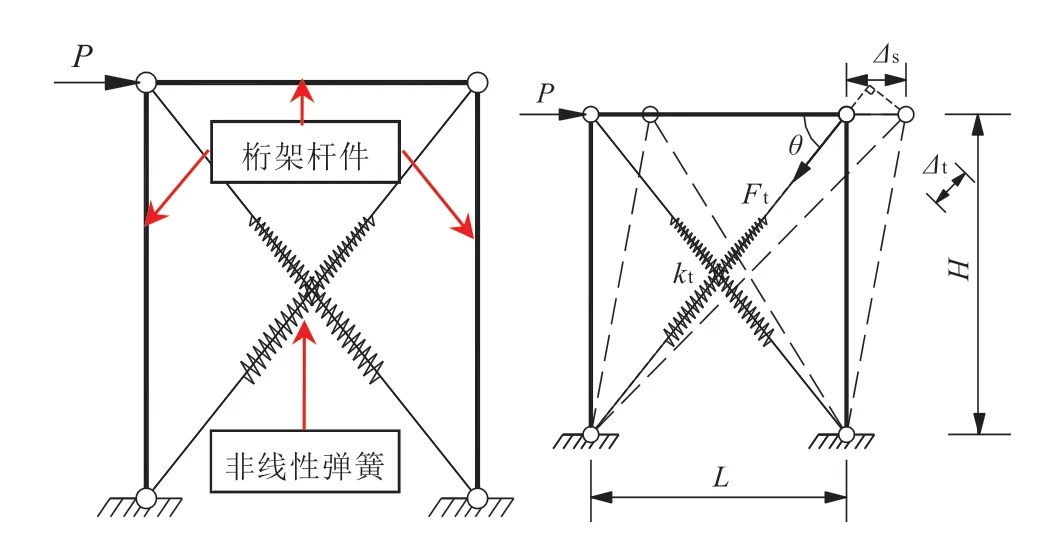
圖2 組合墻體僅發生剪切變形的簡化計算模型Fig.2 Simplified calculation model of composite wall with shear deformation

覆面板主要承擔剪力，等效為非線性對角彈簧以抵抗側向荷載，連接方式為鉸接約束.參考日本輕鋼設計手冊［16］和日本建筑學會木質結構設計規范［17］提出的墻體等代拉條法，可推導墻體剪切變形Δs的計算公式.如圖3 所示，覆面板剪切變形Δ1可參照剪切胡克定律（τ=G·γ）計算得到，見公式（1）（2）.

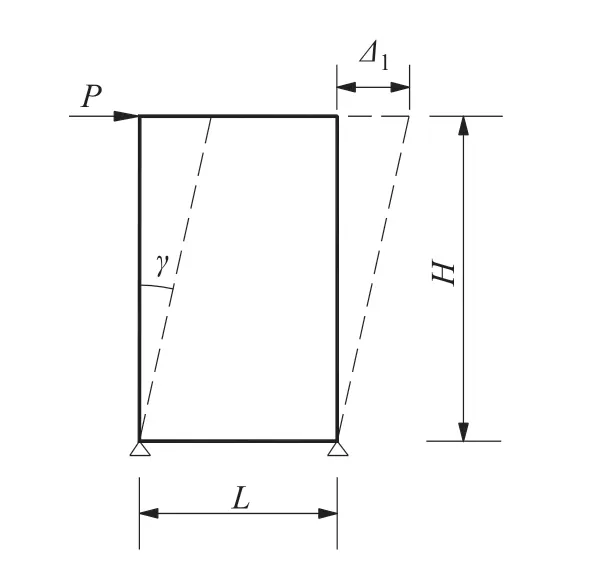
圖3 覆面板剪切變形Fig.3 Shear deformation of cladding panel

式中：τ為切應力；γ為切應變；G為覆面板的剪切模量；P為水平荷載；H為墻體高度；L為墻體寬度；t為覆面板厚度.

參照圖4 計算覆面板上自攻螺釘滑移產生的剪切變形Δ2，簡化分析時假定組合墻體周邊每個自攻螺釘均勻受力，不考慮組合墻體中間墻架柱與覆面板間自攻螺釘的滑移.當組合墻體高寬比（H/L）與相應邊自攻螺釘數目的比值相等時，組合墻體周邊每個自攻螺釘受力相同，即墻體寬度方向，周邊自攻螺釘個數為n，則墻體高度方向，周邊自攻螺釘個數為

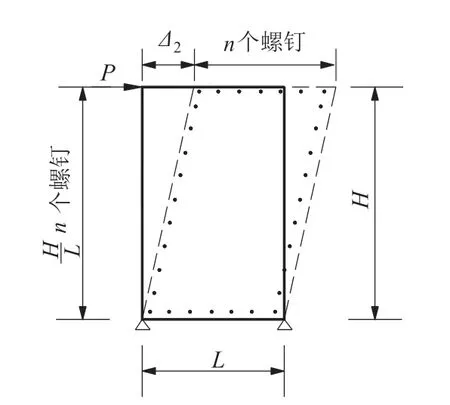
圖4 覆面板螺釘滑移變形Fig.4 Screw slip deformation of cladding panel

在水平荷載P作用下，單個自攻螺釘承擔剪力為N1=P/n，對應的自攻螺釘滑移值為S1；在水平荷載P=1 作用下，單個自攻螺釘承擔剪力為.根據虛功原理，覆面板上自攻螺釘滑移產生的剪切變形Δ2的計算方法見公式（3）（4）.

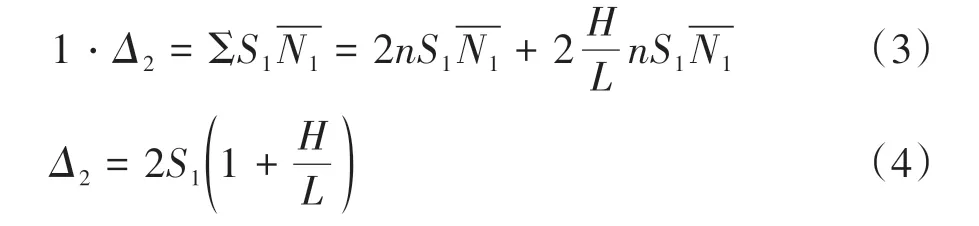
假定當自攻螺釘承擔剪力達到抗剪承載力設計值Nv時，對應的自攻螺釘滑移值為Sv；當自攻螺釘承擔剪力為N1＜Nv時，對應的自攻螺釘滑移為S1，則：

將公式（5）代入公式（4）得：

結合公式（2）和（6），組合墻體的剪切變形Δs計算結果見公式（7）.

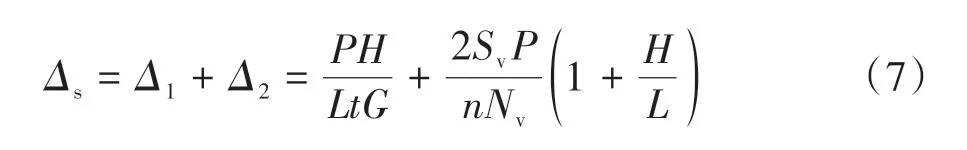
如圖2，簡化計算模型中側向位移Δs的計算方法見公式（8）～（10）.

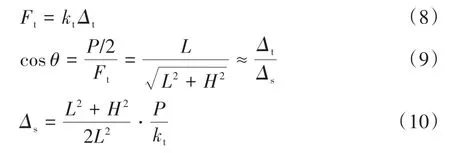
式中：Ft為對角彈簧承受的軸力；Δt為對角彈簧的伸長量；kt為對角彈簧的軸向剛度；θ為對角彈簧與墻體寬度方向的夾角.

聯立公式（7）和（10），得到對角彈簧軸向剛度kt的計算方法，見公式（11）.

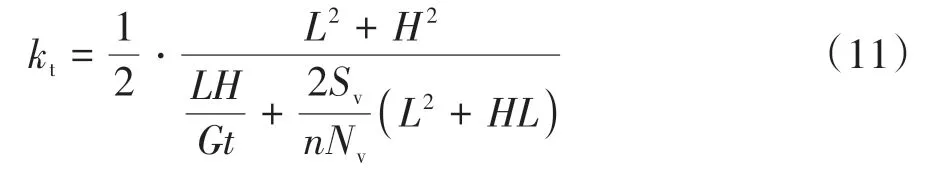
對于實際工程中開設門窗洞口的組合墻體，參照日本規范建議的墻體等代拉條法，考慮組合墻體開洞處上、下墻體的貢獻作用，按照墻體開洞位置將組合墻體劃分為不同尺寸的區格，根據區格的長、寬尺寸，覆面板材料屬性以及周邊自攻螺釘數量與滑移性能，按照公式（11）計算得到不同墻體區格的對角彈簧剛度.綜上，冷彎薄壁型鋼組合墻體考慮剪切變形和彎曲變形的簡化計算模型見圖5，該模型采用非線性對角彈簧模擬分析組合墻體的剪切變形，采用梁式桿件模擬分析組合墻體的彎曲變形.

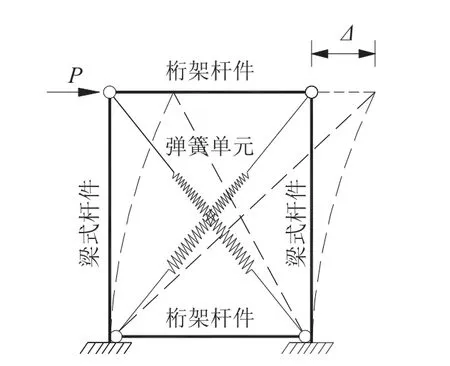
圖5 組合墻體考慮剪切變形和彎曲變形的簡化計算模型Fig.5 Simplified calculation model of composite wall considering shear deformation and bending deformation

2 組合墻體擬靜力試驗模擬分析

為研究冷彎薄壁型鋼組合墻體的側向變形能力，對5 個未開洞和2 個開洞的2.4 m×3 m（寬×高）的組合墻體進行了抗剪性能試驗研究［4-5］.組合墻體試件基本參數見表1，典型試件構造見圖6.采用ABAQUS 有限元軟件對組合墻體簡化計算模型的正確性進行驗證，WA2 試件和WB3 試件有限元模型見圖7.墻體上導軌采用桁架單元T3D2來模擬，單元網格尺寸取為100 mm.墻架柱采用梁單元B31 進行模擬，單元網格尺寸取為100 mm.鋼材采用雙折線本構模型以及von Mises屈服準則，其應力-應變關系參照材性試驗確定［4-5］.耦合上導軌所有節點施加水平位移以模擬位移加載模式，約束墻架柱柱腳節點所有自由度以模擬固端約束.在墻體各區格對角兩個節點間建立彈簧連接約束，連接類型為Axial，受力行為定義為非線性，荷載與位移關系按照公式（11）計算，對應不同受力階段的荷載-位移曲線見圖8.

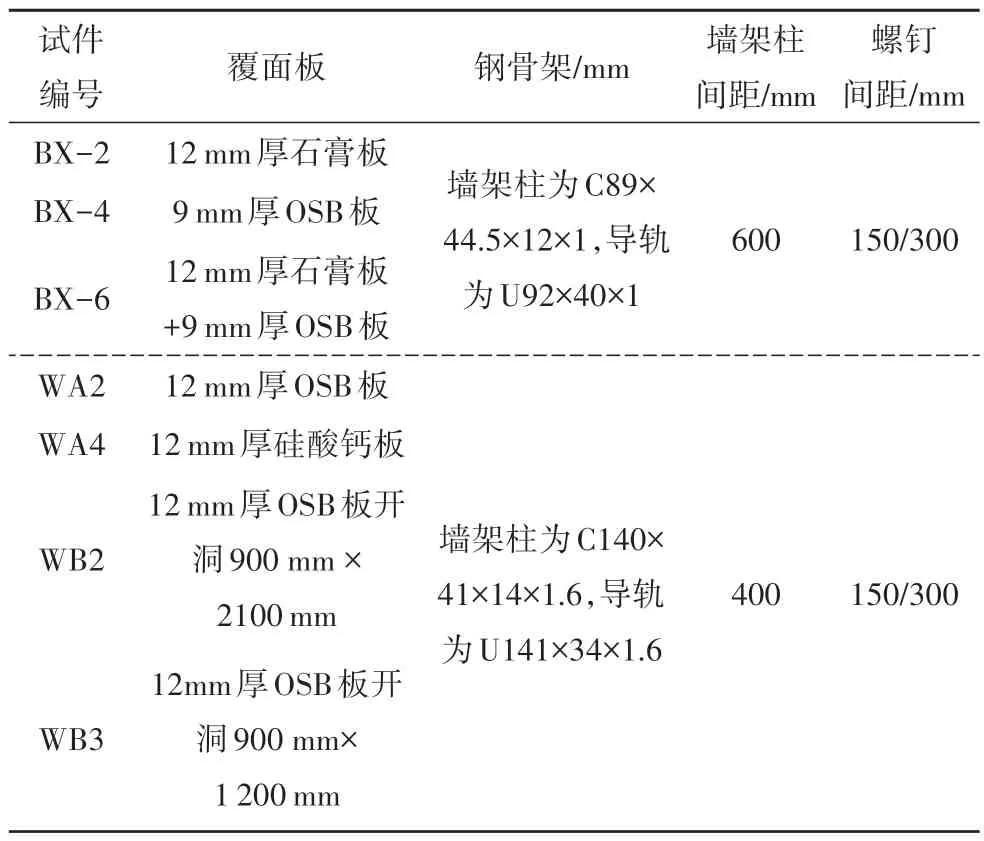
表1 組合墻體試件基本參數Tab.1 Basic parameters of composite wall

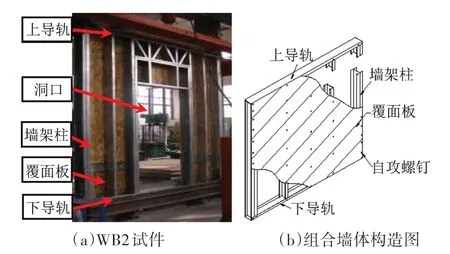
圖6 冷彎薄壁型鋼組合墻體構造Fig.6 Construction of cold-formed thin-walled steel composite wall

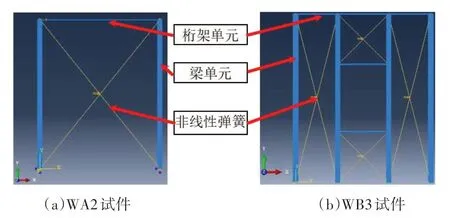
圖7 有限元分析模型Fig.7 Finite element analysis model

圖8 對角彈簧荷載-位移曲線Fig.8 Load-displacement curve of diagonal spring

有限元分析得到墻體WA2 和墻體WB3 在彈性階段的變形云圖見圖9，可知組合墻體變形結果與簡化計算模型變形圖以及試驗結果吻合較好.7 個組合墻體試驗荷載-位移曲線與有限元分析結果對比見圖10，不同受力階段組合墻體承載力指標對比見表2.由圖表可知，組合墻體簡化計算模型能較好地模擬組合墻體試件彈性階段的受力性能，有限元分析結果與試驗結果誤差小于15%，表明采用圖5中組合墻體簡化計算模型來分析組合墻體在彈性階段的抗剪性能是合理的，可滿足基于彈性的設計要求，并為冷彎薄壁型鋼結構住宅的彈性動力時程分析提供參考.在屈服階段和極限階段，墻體承載力有限元分析結果與試驗結果誤差小于10%，而墻體側移有限元分析結果與試驗結果誤差超過20%，表明組合墻體簡化計算模型不能準確模擬墻體在彈塑性階段的剪切變形，主要原因為推導組合墻體剪切變形的過程是建立在彈性條件下，不符合組合墻體在彈塑性階段的受力特性.

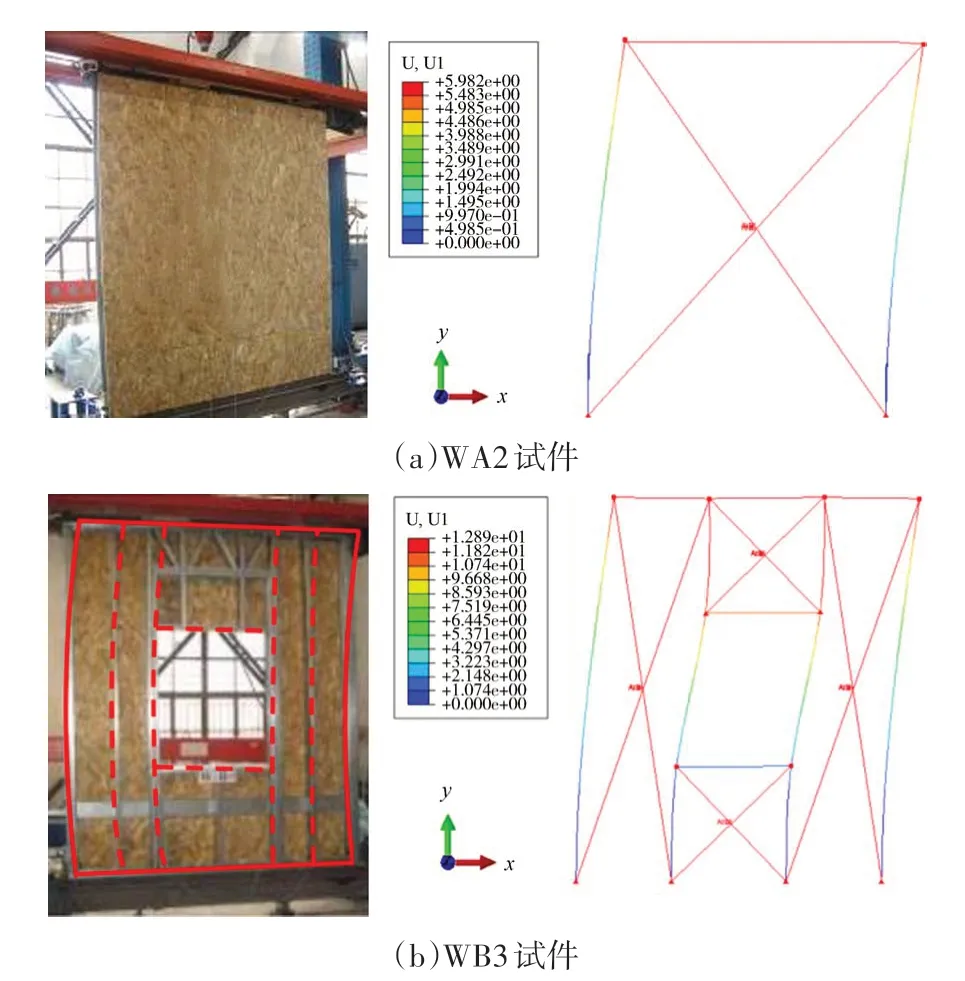
圖9 有限元模型變形圖與試驗對比Fig.9 Finite element model deformation diagram compared with test

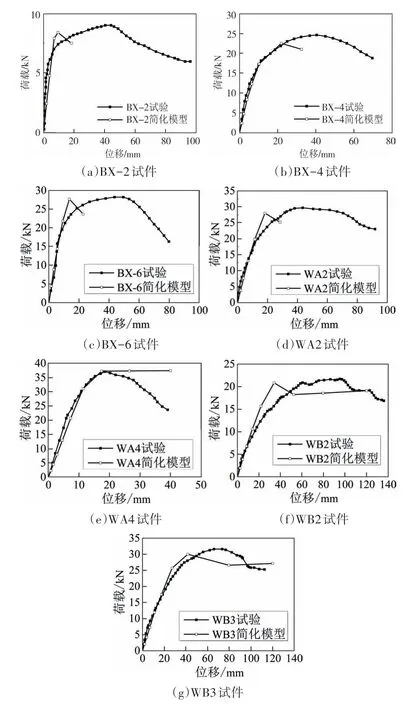
圖10 簡化計算模型荷載-位移曲線有限元與試驗對比Fig.10 The load-displacement curves of simplified calculation model on finite element compared with the test

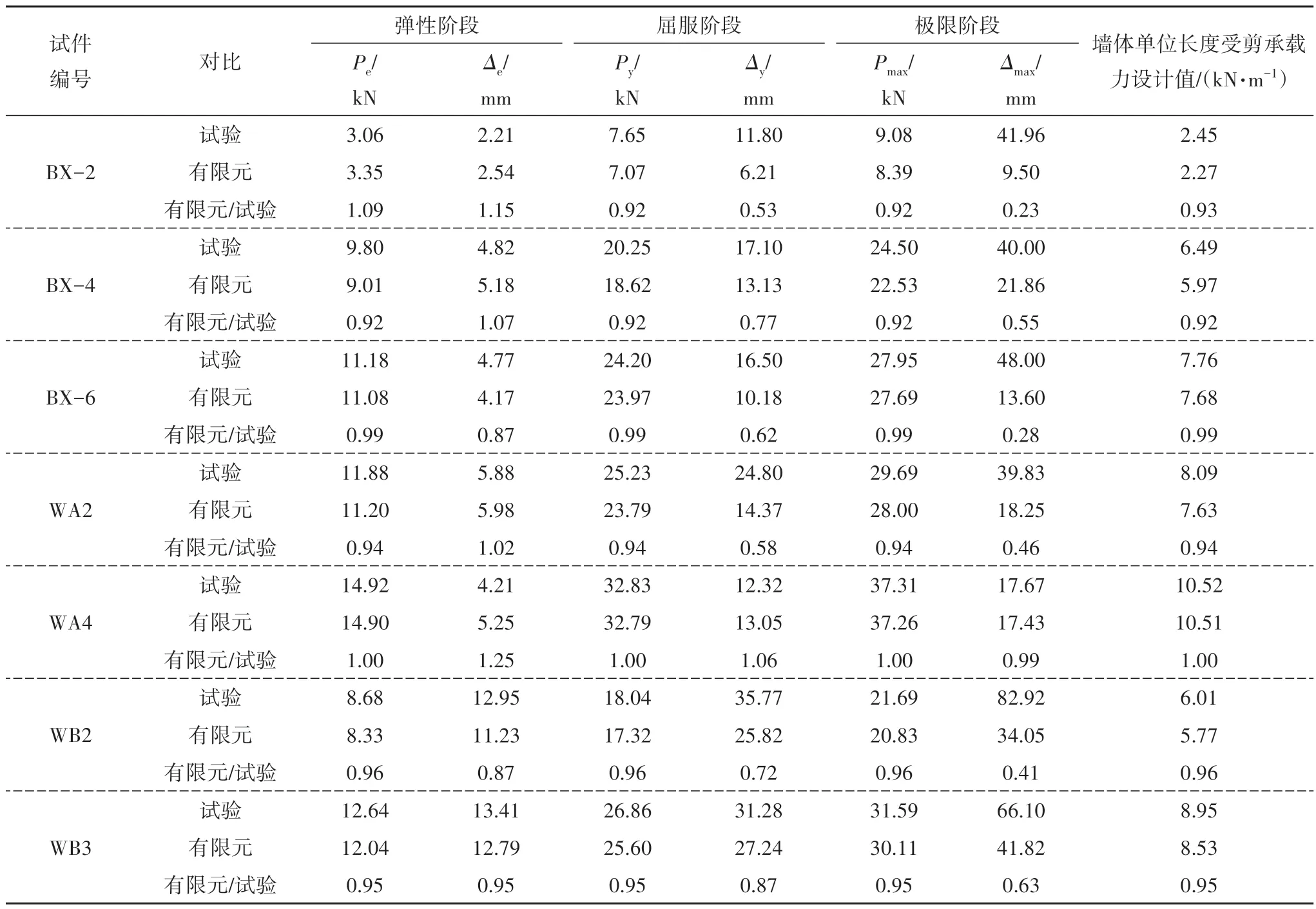
表2 組合墻體承載力指標試驗與有限元對比Tab.2 Test results of composite wall bearing capacity index compared with finite element results

組合墻體試驗試件和有限元分析模型的單位長度受剪承載力設計值見表2，與《低層冷彎薄壁型鋼房屋建筑技術規程》（JGJ 227—2011）［18］和《冷彎薄壁型鋼多層住宅技術標準》（JGJ/T 421—2018）［19］對比可知：組合墻體單位長度的受剪承載力設計值與規范設計值較為接近，而誤差產生的原因為組合墻體試件構造與規范中給定墻體構造不相同，規范中規定的墻體受剪承載力設計值并不能真實反映試驗試件的抗剪性能.

3 輕型鋼結構房屋彈性動力時程分析

文獻［20］對3 層足尺的冷彎薄壁型鋼結構房屋進行了振動臺試驗，試驗模型長度和寬度均為5.1 m，層高為3 m，平面圖和立面圖見圖11.墻架柱規格為C90 mm×35 mm×10 mm×1 mm，鋼材為S350GD+Z 鋼，內墻覆面板為10 mm 厚石膏板，外墻覆面板為 12 mm 厚OSB 板.樓蓋采用鋼桁架梁上覆18 mm 厚OSB 板的組合形式.屋架采用鋼桁架，屋面板為 12 mm厚OSB板.

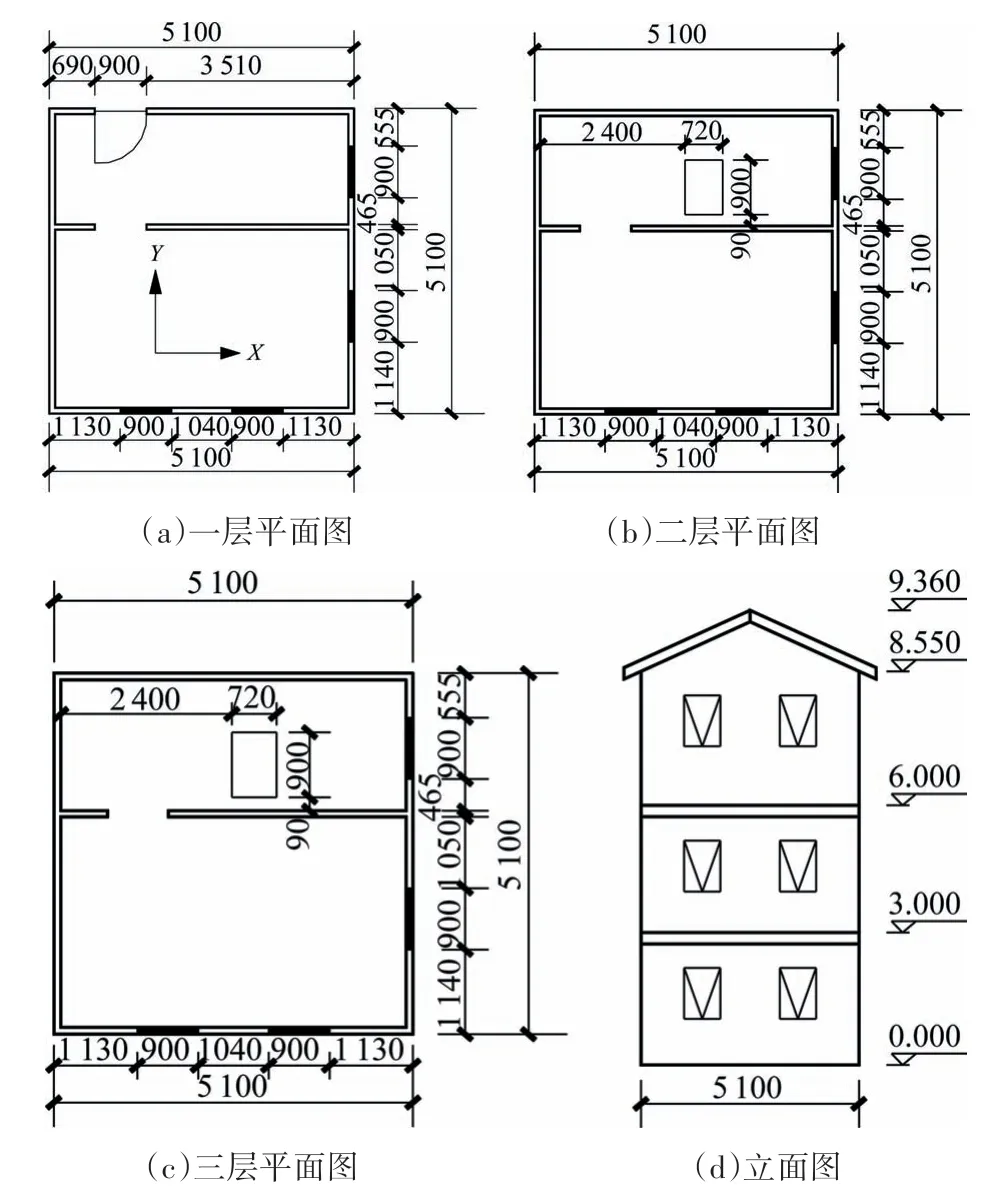
圖11 試驗模型平面圖和立面圖（單位：mm）Fig.11 Plan and elevation of test model（unit：mm）

采用ABAQUS 有限元軟件建立3 層冷彎薄壁型鋼結構房屋模型，見圖12.組合墻體參照圖7 建立，上、下導軌采用桁架單元T3D2 模擬，單元網格尺寸取為200 mm；墻架柱采用梁單元B31模擬，單元網格尺寸取為200 mm.對角彈簧采用非線性彈簧連接單元模擬，連接類型為Axial，彈簧軸向剛度參數按照公式（11）計算.覆面板自重采用集中荷載的方式施加至上導軌兩端.組合樓蓋和屋蓋結合試驗結果確定為剛性樓蓋，采用殼單元S4R 模擬，單元網格尺寸取為400 mm.鋼材采用雙折線本構模型以及von Mises 屈服準則，其應力-應變關系參照材性試驗確定［20］.石膏板和OSB板簡化為各向同性板件，材料參數參照材性試驗確定［20］.在材料屬性中定義瑞利阻尼參數，阻尼比采用3%.在坐標系Z向定義重力加速度g=9.8 m/s2以模擬結構自重，樓、屋面活荷載采用均布荷載模擬.約束墻架柱柱腳節點所有自由度以模擬固端約束.

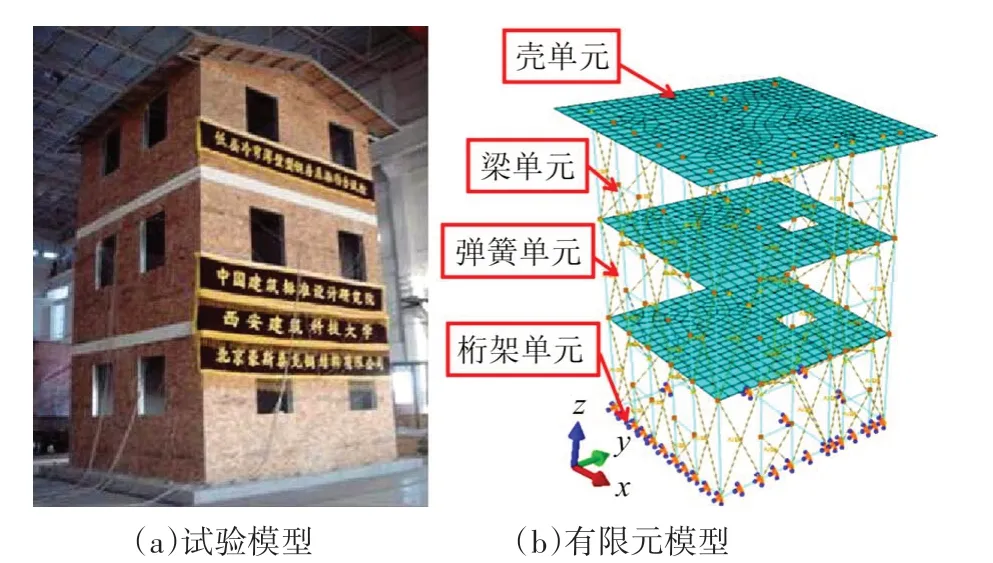
圖12 3層房屋有限元模型Fig.12 Finite element model of three-storey building

3.1 模態分析

有限元模態分析得到模型前3 階自振頻率見表3，前3 階振型見圖13.由圖和表可知：有限元模型的前3 階振型均為整體變形，其中1 階振型為沿Y向的平動，2階振型為沿X向的平動，3階振型為繞Z向的扭轉.有限元模型分析得到房屋自振頻率和周期與試驗結果吻合較好，誤差小于10%，表明有限元模型可較好地模擬房屋動力特性，且簡單、合理.

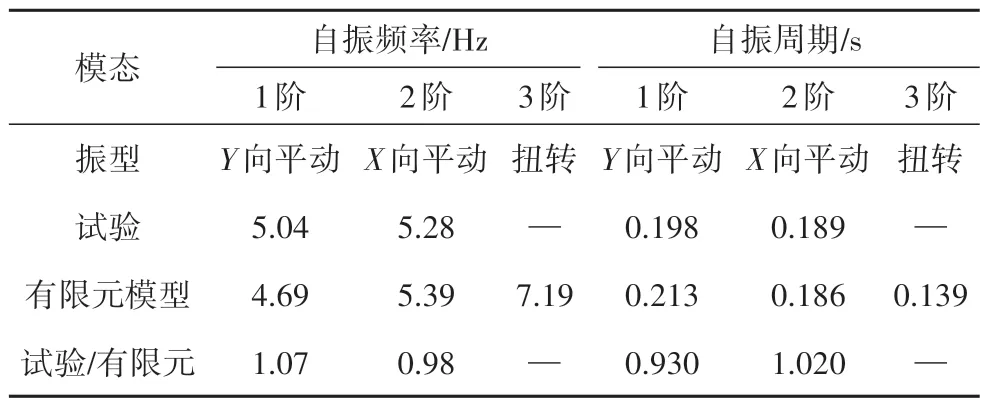
表3 模型前3階自振頻率及周期Tab.3 The first three natural frequencies and periods of the model

3.2 彈性動力時程分析

按振動臺試驗加載工況［20］，見表4，釋放有限元模型墻架柱柱腳節點X和Y方向自由度，施加7 度和8度多遇El Centro調幅波，對有限元模型進行彈性動力時程分析.有限元模型在4 個工況下1 至3 層最大加速度放大系數變化曲線試驗與有限元對比見圖14，最大相對位移變化曲線試驗與有限元對比見圖15.

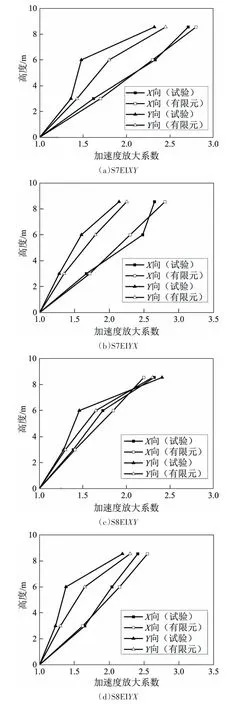
圖14 最大加速度放大系數變化曲線試驗與有限元對比Fig.14 Test results of maximum acceleration amplification coefficient variation curves compared with finite element results

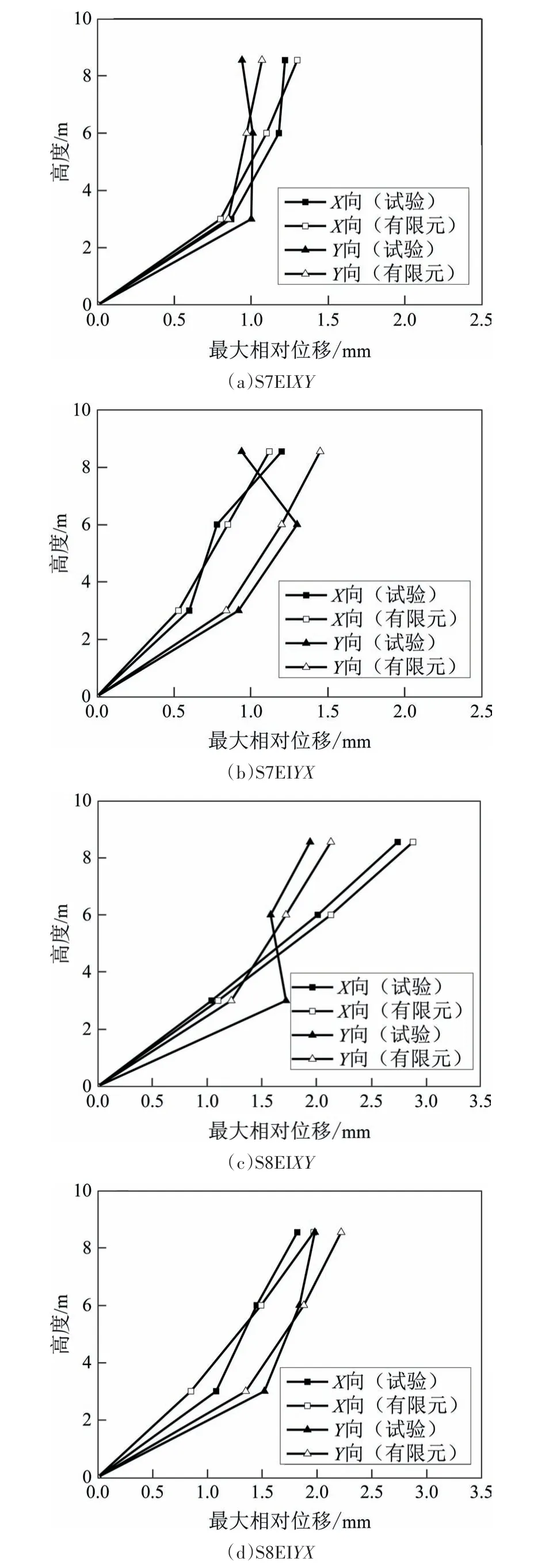
圖15 最大相對位移變化曲線試驗與有限元對比Fig.15 Test results of maximum relative displacement variation curves compared with finite element results

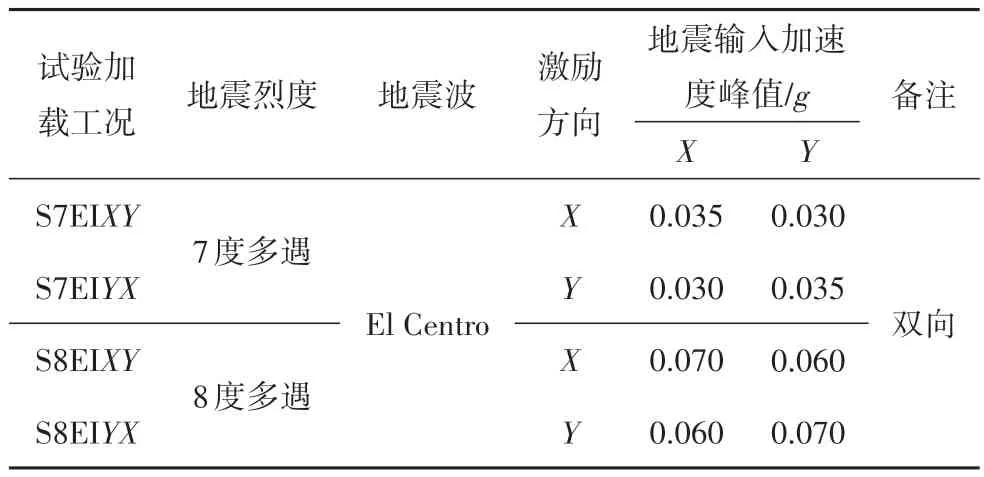
表4 有限元模型加載工況Tab.4 Loading condition of finite element model

由圖可知：在7 度多遇和8 度多遇地震作用下，有限元模型1～3 層相同測點加速度峰值和最大相對位移試驗結果與有限元分析結果吻合較好，誤差小于15%，最大加速度放大系數變化曲線和最大相對位移變化曲線試驗結果與有限元分析結果變化規律和整體趨勢相近.誤差主要出現在模型2層和3層在Y向的加速度響應和位移響應，原因為3 層房屋模型先后經歷了一系列的試驗加載工況，出現了結構損傷累積，如抗拔件松動、覆面板開裂等破壞現象，試驗模型的整體性降低，而有限元模型較為理想，僅對單一加載工況進行模擬，未能考慮房屋模型經歷多次加載工況而造成的損傷累積對房屋剛度的折減.因此，有限元模型能較合理及準確地模擬3 層冷彎薄壁型鋼結構房屋在多遇地震作用下的動力響應，有限元模型簡單、合理.

同時，圖5 建立的組合墻體簡化計算模型能較好地應用于冷彎薄壁型鋼結構住宅的彈性動力時程分析，對工程設計和數值分析具有較好的應用價值.

4 結 論

基于冷彎薄壁型鋼組合墻體簡化計算模型，通過對組合墻體抗剪性能試驗和3 層房屋振動臺試驗的模擬分析，得出以下結論：

1）在水平荷載作用下，組合墻體的側向變形以剪切變形和彎曲變形為主.將覆面板等效為非線性對角彈簧以分析墻體的剪切變形，將墻架柱等效為梁式桿件以分析墻體的彎曲變形.推導出對角彈簧的軸向剛度計算方法.

2）基于墻體等代拉條法建立的組合墻體簡化計算模型適用于結構的彈性分析，當結構進入彈塑性狀態時，該模型會出現較大誤差.基于組合墻體簡化計算模型和剛性樓板假定建立的3 層冷彎薄壁型鋼結構房屋有限元模型能較好地模擬輕鋼房屋的動力特性以及多遇地震作用下的動力響應.

3）在工程設計時，若需要對組合墻體進行全過程模擬或對整體房屋進行彈塑性動力時程分析，建議采用試驗測取的荷載-位移曲線來計算對角彈簧的軸向剛度或在簡化計算模型的對角彈簧單元中引入塑性本構和損傷機制以滿足彈塑性設計要求.