兩種新型鋼管混凝土格構式風電塔架節點損傷機理對比分析

聞洋 ，吳夏至 ?，熊林 ，熊文

（1.內蒙古科技大學 土木工程學院，內蒙古 包頭 014010；2.廣東工商職業技術大學 建筑工程學院，廣東 肇慶 526000）

新能源革命是未來數十年能源和電力產業最大的變革趨勢，我國正在成為全球新能源革命的中心，風力發電在新能源革命中的地位舉足輕重［1］.隨著發電機組裝機容量越來越大型化，對于風電塔架的要求也越來越高.格構式風電塔架憑借其運輸方便、拆裝便利、剛度大、用鋼量少等優點將會擁有廣闊的發展前景［2-4］.

在格構式風電塔架節點的研究中，傳統式的相貫節點和管板節點已經取得了相對完備的理論成果，但兩者都存在高空施焊、焊接效果不理想、殘余應力復雜等缺點［5-10］，因此探尋新的節點形式對于格構式風電塔架的發展具有重大的意義.為此，課題組基于裝配式節點的概念先后研究了螺栓球節點、桿式分支等節點［11-14］.上述節點具有現場免施焊、拆裝便利等優點，但因其腹桿合力未交于塔柱中心，引起附加彎矩造成了節點剪切破壞.這對裝配式節點的推廣使用十分不利.

基于此，課題組提出了分體球型節點與橢球型節點兩種不同的解決方案.兩種節點的腹桿合力均能交匯于塔柱中心，傳力路徑明確合理.本文開展了兩個分體球型節點和兩個橢球型節點的靜力試驗研究，以期得到兩種節點的應力分布規律及破壞模式，并以此分析兩種節點優勢與弊端，對裝配式節點形式的進一步探索提供試驗依據與理論支持.

1 試驗概況

1.1 試件設計

以內蒙古白云鄂博礦區風電場某1.5 MW 錐筒塔架為原型，結合《鋼結構設計規范》（GB50017—2017）［15］和《高聳結構設計規范》（GB50135—2019）［16］，通過SAP2000軟件進行內力分析，建立鋼管混凝土四肢柱風電塔架模型.根據試驗場地、加載設備的情況按照1∶1.6 的比例設計了2 個分體球型節點和2個橢球型節點.節點構造如圖1所示.

圖1 節點構造示意圖Fig.1 Node structure diagram

分體球型節點與橢球型節點的塔柱、腹桿均采用20Mn 無縫鋼管，塔柱采用C40 混凝土進行填充.球臺、球臺蓋板采用Q235 鋼，圓螺栓球與橢球型螺栓球采用45#鋼切削而成，球臺與球臺壓板使用M20高強螺栓鎖緊，腹桿與螺栓球間采用10.9 級M27 高強螺栓連接，采用坡口焊的焊接方式將球臺焊接在包裹體上.試件主要參數見表1.鋼材的力學性能見表2.

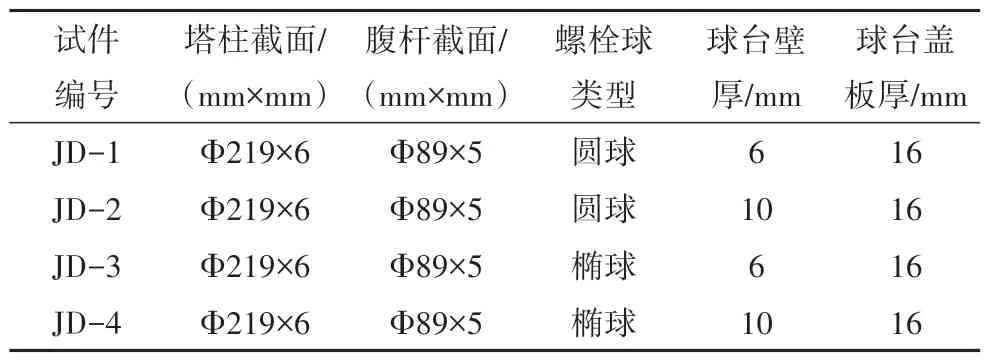
表1 試件主要參數Tab.1 Main parameters of specimens

表2 鋼材力學性能指標Tab.2 Mechanical properties of steel MPa

1.2 加載裝置及加載制度

加載方式采用臥位加載，塔柱右側底板通過高強螺栓與承力支座連接，地腳螺栓將承力支座與地槽卡死，塔柱左側放置在半圓形支撐架上，上部半圓形卡扣通過高強螺栓將塔柱鎖緊.試驗采用兩臺液壓伺服器，一端與受拉、壓腹桿的加載板相連，另一端通過錨桿與重力反力墻固定.受壓側伺服作動器與腹桿相連處設置防側移裝置，避免出現附加彎矩使受壓腹桿出現側移.加載裝置示意圖見圖2.

圖2 加載裝置Fig.2 Test setup

試驗采用荷載控制的加載方式，分為預加載階段、標準加載階段和破壞加載階段，壓、拉腹桿采取1.05∶1 的比例加載.根據ABAQUS 軟件進行非線性分析得到極限理論荷載.正式試驗前進行預加載，保證各試驗儀器能夠正常工作；標準加載階段每級荷載增量取極限荷載的10%，當荷載增加至極限荷載的85%或試件出現明顯的塑性變形時，試件進入破壞加載階段，荷載增量降為極限荷載的5%；當試件出現明顯破壞時，試驗停止.

2 試件破壞形態

試件JD-1 表現為球臺材料強度破壞，如圖3（a）所示.初始加載階段無明顯現象，當受拉側荷載為160 kN 時，球臺壓板內緣出現輕微變形；當受拉側荷載增大到214 kN時，球臺壓板與球臺的間隙增大；當荷載繼續增大至288 kN 時，受拉側球臺從冠點焊縫處被完全拉斷，試驗結束.試件JD-2 表現為球臺壓板屈曲破壞，如圖3（b）所示.初始加載階段無明顯現象，當受拉側荷載達到245 kN時，球臺壓板內緣出現輕微屈曲；荷載增大至298 kN時，球臺與球臺壓板間出現不均勻的間隙；當荷載達到347 kN時，球臺壓板內緣屈曲嚴重造成螺栓球被拉出，試驗結束.試件JD-3 表現為球臺壓板撕裂破壞，如圖3（c）所示.初始加載階段無明顯現象，當受拉側荷載為198 kN時，球臺承板與球臺壓板間出現細微間隙；荷載達到305 kN 時，受拉側球臺壓板微微隆起，出現細微裂縫；最終當荷載達到346 kN 時，裂縫貫通，試驗結束.試件JD-4 表現為受拉腹桿螺栓螺紋破壞，如圖3（d）所示.初始加載階段無明顯現象，當受拉側荷載為245 kN 時，球臺與球臺壓板出現輕微的塑性變形；荷載繼續增加至390 kN 時，受拉腹桿的高強螺栓突然被拔出，試驗結束.

圖3 節點破壞形態Fig.3 Node destruction form

3 試驗結果及分析

3.1 試件荷載-變形曲線

圖4 所示為節點腹桿荷載-變形關系曲線圖，規定腹桿受拉時位移值為正值，腹桿受壓時位移值為負值.JD-1與JD-2曲線受拉側在加載初期呈線性增長，且兩條曲線基本吻合.當荷載增大至214 kN 時，JD-1 曲線斜率開始下降，兩條曲線開始分離；當荷載增大至288 kN 時，JD-1 的球臺被拉斷；當荷載達到298 kN 時，JD-2 的曲線斜率也逐漸下降，這是由于球臺壓板逐漸屈曲出現塑性變形導致；當荷載增大至347 kN 時，螺栓球被拉出.JD-3 加載初期受拉側曲線呈線性增長，當荷載增大至305 kN時，斜率大幅下降，這是由于球臺壓板內緣坡口出現裂縫所致；當荷載達到346 kN 時，球臺壓板裂縫完全貫通.JD-4 加載初期受拉側曲線呈線性增長；當荷載增長到390 kN 時，受拉腹桿的高強螺栓突然從橢球中被拉出，試驗結束.

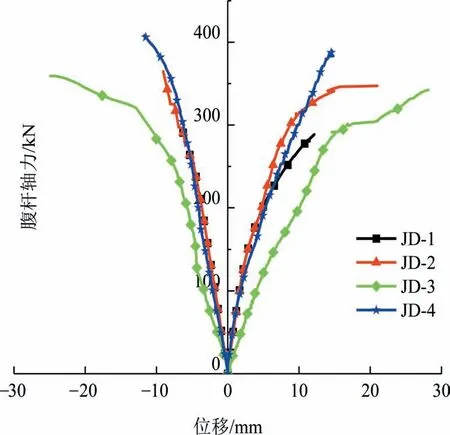
圖4 腹桿荷載-變形關系曲線Fig.4 Load-deformation curves of specimens

分析分體球型節點的腹桿荷載-變形關系曲線可以發現，JD-1與JD-2的曲線斜率在彈性階段基本保持一致，說明分體球型節點在彈性工作階段，球臺壁厚的增長對節點的變形能力影響并不明顯.當試件JD-1 與JD-2 進入塑性變形階段時，JD-2 腹桿的極限位移相對于JD-1 多9 mm，塑性發展階段更長.這是由于球臺壁厚由6 mm 增大至10 mm，球臺軸向抗拉承載力大幅提高，節點破壞模式由球臺被拉斷轉變為球臺壓板屈曲破壞，節點承載力增大20.5%.分析橢球型節點的腹桿荷載-變形關系曲線可知：在全段曲線中，JD-4的曲線斜率明顯大于JD-3，且JD-4 曲線彈性階段比JD-3 更長，節點極限承載力提高12.7%.說明橢球型節點隨著球臺壁厚的增大，節點區剛度顯著增加，節點極限承載力顯著增強.

綜上，對比分析兩種節點的腹桿荷載-變形關系曲線可得：在相同壁厚條件下，橢球型節點的彈性工作階段比分體球型節點更長，承載能力更佳；且在彈性工作狀態下，當球臺壁厚由6 mm增長至10 mm時，橢球型節點的曲線斜率較分體球型節點有了大幅提升，表明球臺壁厚的增加顯著提升了橢球節點的整體剛度，但對分體球型節點的整體剛度提升不大.

3.2 球臺區應力分布

球臺是固定螺栓球和連接包裹體的主要構件，且存在大量焊縫，球臺區應力分布情況十分復雜，對球臺區等效應力的研究十分重要.圖5 為球臺測點布置圖，圖6為等效應力分布圖.

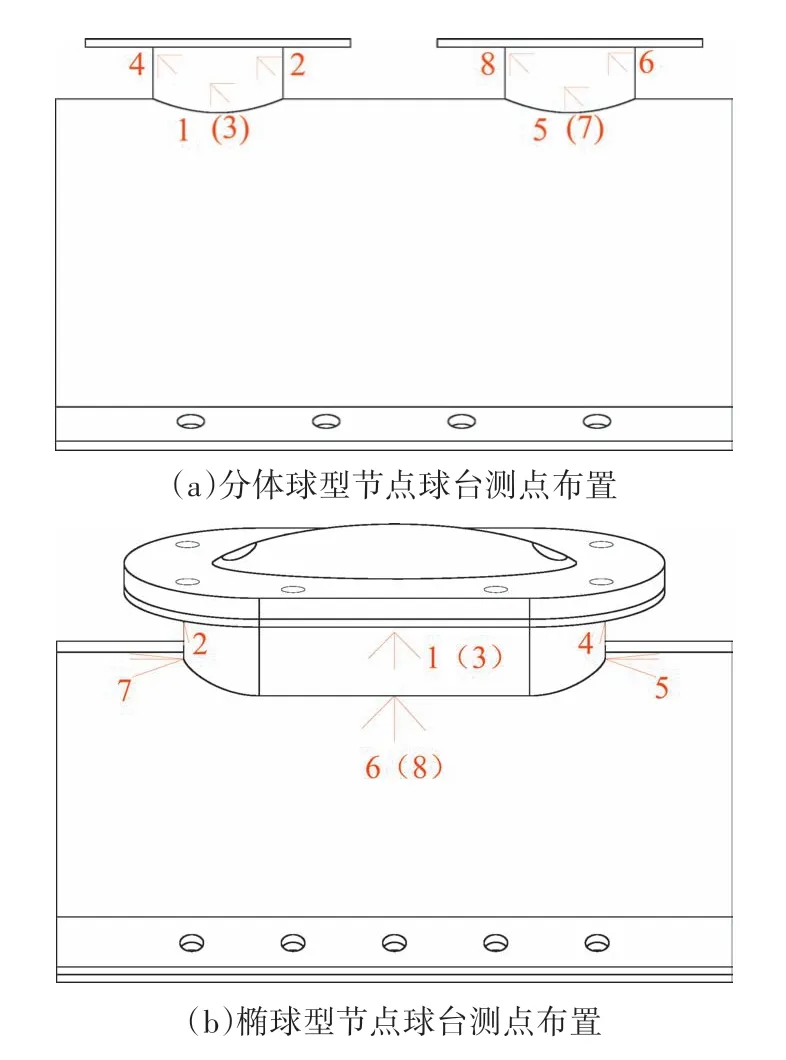
圖5 球臺測點布置Fig.5 Monitoring points arrangement of table area

圖6 球臺區等效應力分布曲線Fig.6 Equivalent stress distribution curves of table area

分析分體球型節點球臺等效應力可知：1～4號為壓區球臺測點，5～8 號為拉區球臺測點.拉區球臺的等效應力整體要高于壓區球臺等效應力，在JD-1 與JD-2中，壓區球臺最大等效應力均出現在2號測點，分別為103 MPa、149 MPa；最小等效應力出現在1 號測點和3 號測點，分別為64 MPa、9 MPa.最大等效應力分別為最小應力的1.6 倍和17 倍.拉區球臺最大等效應力出現在7 號測點和8 號測點，分別為307 MPa、256 MPa；最小等效應力均出現在6 號測點，分別為168 MPa、79 MPa.最大等效應力分別為最小等效應力的1.8倍、3.2倍.2號測點表現為壓應力，這是由于螺栓球在推力的作用下與球臺壁碰撞擠壓.對于JD-1，當荷載增大至260 kN 時，7 號測點的等效應力出現躍升，這是由于球臺在拉力作用下焊縫出現裂縫.荷載達到288 kN 時，6號、7號測點再次發生躍升，這是由于球臺根部的裂縫已經貫通，球臺被拉斷，試驗結束.對于JD-2，各測點的應力增長較為均勻，當荷載增長至347 kN 時，球臺壓板屈曲，螺栓球被拉出，試驗結束.對比試件JD-1與JD-2，球臺壁厚由6 mm 增大至10 mm 時，節點承載力增大了20.5%，最大等效應力值下降了16%.球臺的軸向剛度顯著提高，應力增長更加均勻，應力耗散能力更強.

分析橢球型節點球臺等效應力可知：JD-3、JD-4等效應力最大值與最小值分別出現在3 號、4 號測點和8 號、2 號測點，最大等效應力分別為最小等效應力的9.7 倍和7.1 倍.1 號、3 號測點出現較大幅度的應力增長，這是由于橢球在腹桿的拉、壓作用下易出現平面外偏轉，使橢球腹部與1 號、3 號測點擠壓加劇.對于JD-3，當荷載達到150 kN 時，4 號測點由壓應力轉為拉應力，這是由于球臺出現塑性變形，橢球偏轉與球臺壁產生相對滑動.當荷載達到300 kN時，拉應力又轉化為壓應力，這是由于球臺壓板出現屈曲，橢球尖端偏轉程度加大，橢球尖端被拉出球臺外緣，對4 號測點造成擠壓.對于JD-4，4 號測點的等效應力有了最大幅度的提升，這是由于橢球尖端與4 號測區碰撞最為劇烈，當荷載達到250 kN、300 kN 時，4 號測點的應力均出現躍升，原因是球臺由于橢球擠壓出現塑性變形.對比試件JD-3 與JD-4，球臺壁厚由6 mm 增大至10 mm 時，節點承載力增大了12.7%，最大等效應力值下降了33%.在相同荷載作用下，各測點的等效應力顯著下降.

綜上，對比分析兩種節點球臺區的等效應力分布情況發現，相對于橢球型節點，分體球型節點球臺區等效應力分布更為均勻，等效應力極差更小，應力集中現象不明顯，表明分體球型節點球臺受力更均勻，材料利用率更高.當球臺壁厚由6 mm 增長至10 mm 時，兩種節點的極限承載力均顯著提升，并有效降低了相同荷載作用下球臺的等效應力，表明球臺壁厚是影響節點承載力的關鍵因素.

3.3 球臺壓板應力分布

球臺壓板是束縛螺栓球的主要承力構件，試驗中兩種節點的球臺壓板均出現不同程度的損壞，探尋兩種節點球臺壓板區等效應力分布情況對分析節點的受力模式具有重要意義.圖7 為球臺壓板區的測點布置圖，圖8為等效應力分布圖.

圖7 球臺壓板測點布置Fig.7 Monitoring points arrangement of ball table pressing plate

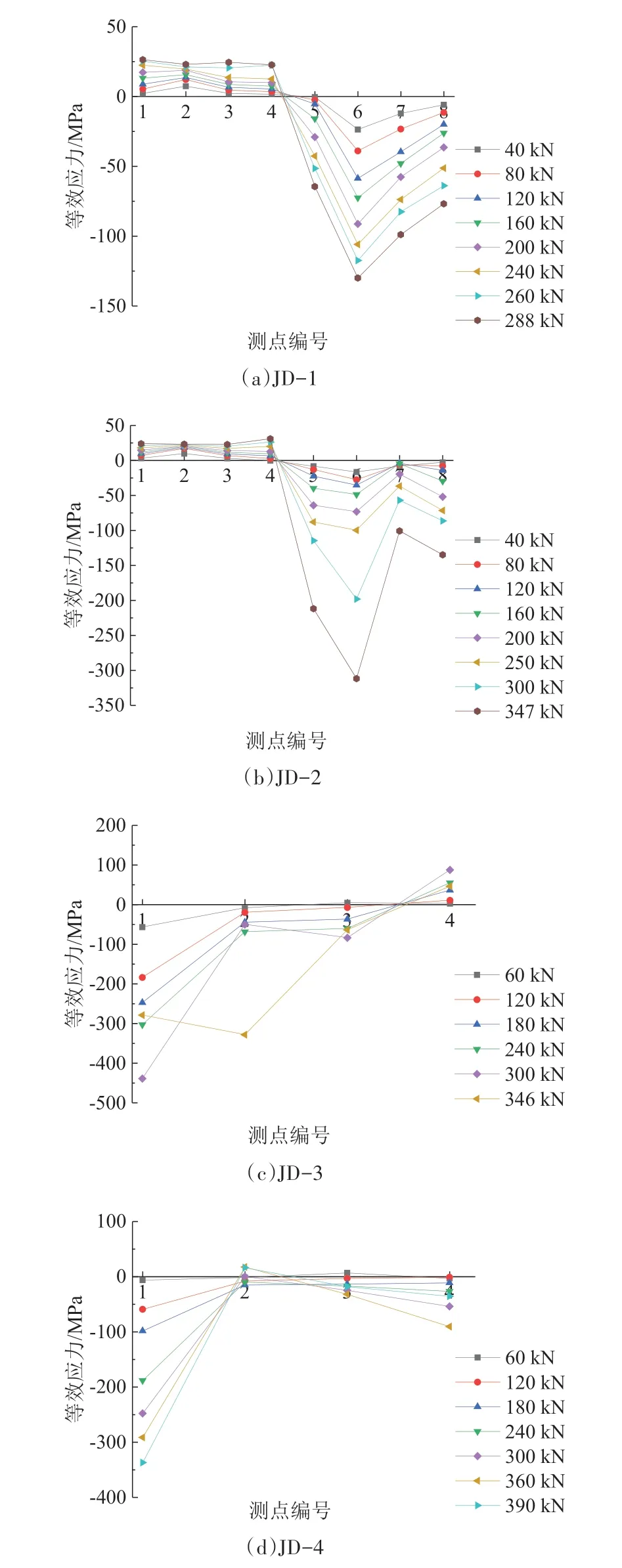
圖8 球臺壓板等效應力分布曲線Fig.8 Equivalent stress distribution curve of ball table pressing plate

分析分體球型節點球臺壓板等效應力可知：試件JD-1、JD-2 中1～4 號測點應力增長并不明顯，原因是在受壓區球臺壓板與螺栓球相互作用很小，球臺壓板僅起構造作用.分析5～8 號測點的等效應力可知，拉區球臺壓板的最大等效應力均出現在6 號測點，分別為130 MPa、311 MPa；最小等效應力分別出現在5 號測點和7 號測點，為65 MPa、100 MPa.最大等效應力分別為最小等效應力的2 倍和3.1 倍.表明分體球型節點球臺壓板等效應力分布比較均勻，等效應力極差不大.對于試件JD-1，球臺壓板的等效應力水平整體偏低，這是由于拉區球臺被拉斷，球臺壓板的作用未被充分發揮.對于試件JD-2，當荷載增大到300kN、347 kN 時，6 號測點應力發生躍升，原因是在受拉腹桿作用下，螺栓球對6 號測點的擠壓加劇，造成球臺壓板進一步屈曲.對比試件JD-1與JD-2，球臺壁厚由6 mm 增長至10 mm，球臺壓板各測點等效應力增長明顯，6號測點最大等效應力值增長了139%，表明球臺壁厚的增長使得球臺壓板受力程度加大.

分析橢球型節點球臺壓板等效應力可知：JD-3、JD-4球臺壓板最大等效應力均出現在1號測點分別為438 MPa、337 MPa；最小等效應力出現在2 號測點分別為50 MPa、16.2 MPa.最大等效應力分別為最小等效應力的8.7 倍、20.8 倍，表明球臺壓板區等效應力分布不均勻，等效應力極差相對較大.對于試件JD-3，當荷載達到346 kN 時，1 號測點應力大幅減小，2 號測點應力出現躍升，這是由于球臺壓板裂縫完全貫通、應力重分布所致.對于試件JD-4，由于受拉腹桿螺栓被拉出，球臺壓板的作用未被完全發揮，除1 號測點外，其余測點的應力增長幅度較小.對比試件JD-3 與JD-4，當球臺壁厚由6 mm 增長至10 mm，在相同荷載作用下，球臺壓板各測點等效應力顯著下降，1 號測點最大等效應力值降低23%，表明球臺壁厚的增加顯著降低了球臺壓板的等效應力水平，改善了球臺壓板的工作性能，提高了球臺壓板的安全儲備.

綜上，對比兩種節點球臺壓板等效應力分布情況發現：橢球型節點相較于分體球型節點，球臺壓板區的等效應力分布更為分散，等效應力極差更大.原因是分體球型節點受力時，螺栓球與球臺壓板內緣緊密貼合，受力較為均勻，使得球臺壓板在破壞時表現為壓板內緣整體平面外屈曲.而橢球型節點在受力過程中橢球易發生偏轉，使得受拉側橢球尖端與球臺壓板碰撞擠壓，造成此區域的應力大幅增長，應力集中現象顯著.

3.4 節點破壞模式對比分析

綜合試驗破壞形態與試件受力情況，對兩種節點的破壞模式進行對比分析可知：對于分體球型節點，球臺壁厚為6 mm 時，球臺軸向抗拉承載力不足，節點的破壞模式表現為球臺材料強度破壞.球臺壁厚增長為10 mm 時，球臺的軸向抗拉承載力顯著增加，球臺壓板的平面外剛度不足造成球臺壓板內緣屈曲，節點的破壞模式轉變為球臺壓板屈曲破壞.對于橢球型節點，球臺壁厚為6 mm 時，球臺在橢球碰撞擠壓下出現塑性變形，橢球發生偏轉與球臺壓板發生擠壓導致球臺壓板撕裂.當球臺壁厚由6 mm 增長至10 mm 時，球臺的徑向剛度極大提高，產生的塑性變形減小，對橢球的束縛作用增強，此時受拉側腹桿螺栓出現“滑絲”現象，螺紋失效，節點破壞模式由球臺壓板撕裂轉變為螺栓螺紋破壞.

對比兩種節點的破壞模式可知，由于兩種節點的構造形式不同導致球臺的破壞模式存在明顯差異.分體球型節點在受力時球臺主要受腹桿傳遞的豎直分力，球臺破壞時表現為沿球臺根部焊縫薄弱區整體被拉斷.橢球型節點在受力時拉、壓腹桿共同作用在橢球上產生一個水平合力，使橢球尖端與球臺壁碰撞擠壓，球臺的破壞形態主要表現為徑向的塑性變形.

綜上，節點的構造形式與球臺壁厚度對兩種節點的破壞模式具有重要影響.橢球型節點螺栓螺紋破壞突然，破壞時沒有先兆，屬于一種不安全的破壞模式.在節點設計時，螺栓的擰入深度應適當加大，以杜絕此種破壞模式的發生.

4 有限元分析

為了與試驗結果進行對比，以及更為全面地分析球臺壁厚對節點的破壞機理和影響規律，采用ABAQUS 有限元分析軟件對試件的受力性能進行參數擴展分析.

4.1 有限元模型

鋼材的材料屬性采用韓林海給出的二次塑流模型，核心混凝土的材料屬性采用韓林海提出的混凝土應力-應變關系模型，混凝土塑性階段采用塑性損傷模型定義［17］.混凝土和鋼管、螺栓球與球臺和球臺壓板的接觸界面在法線方向采用硬接觸，在切線方向采用罰摩擦，取摩擦因數為0.6和0.15.

通過非線性分析得出承載力計算值與試驗值，經對比可發現，兩者誤差率基本保持在10%以內，且模擬試件的破壞特征與試驗時的破壞特征基本吻合，表明有限元模擬的精度滿足要求，可以依此對球臺壁厚度進行參數擴展分析.承載力數值對比見表3，試驗破壞特征對比見圖9.

圖9 試驗破壞特征對比Fig.9 Comparison of test failure characteristics

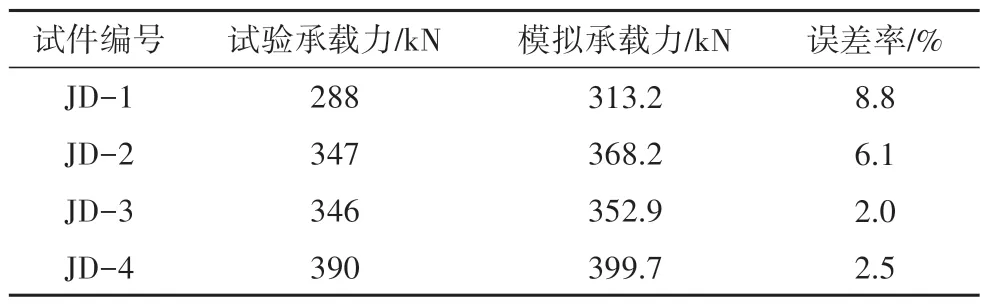
表3 節點承載力對比Tab.3 Node bearing capacity comparison

4.2 參數擴展分析

因試驗中試件數量過于局限，故利用ABAQUS有限元分析軟件對球臺壁厚進行參數擴展分析，對分體球型節點和橢球型節點分別建立8 個有限元模型，參數擴展分析表見表4.圖10 為模型承載力與球臺壁厚關系曲線.

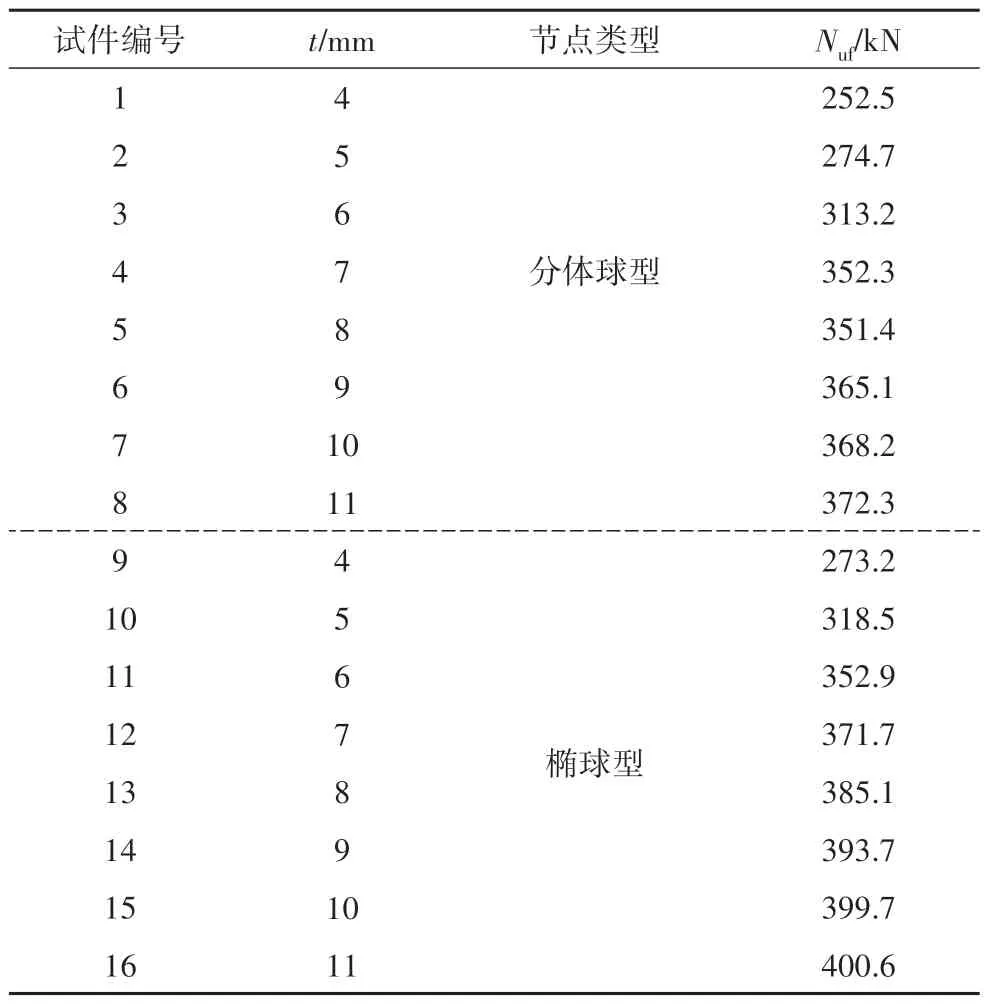
表4 參數擴展分析Tab.4 Parameter expansion analysisz

由圖10 可得：隨著球臺壁厚的增加，兩種節點的極限承載力均有顯著提升.對于橢球型節點，模型極限承載力的增幅隨著球臺壁厚的增長逐漸減小，當球臺壁厚為9 mm 時，模型承載力的增長到達瓶頸期，這是由于球臺徑向剛度顯著提高，抵抗變形的能力極大提升，此時隨著球臺壁厚繼續增加，節點承載力增幅顯著放緩.對于分體球型節點，當球臺壁厚由4 mm 增長至7 mm 時，模型極限承載力增長幅度較大；當球臺壁厚由7 mm 增長至11 mm 時，模型承載力的增長進入平臺期.原因是球臺壁厚的增長極大提升了球臺的軸向抗拉承載力，使得節點的破壞模式由球臺材料強度破壞轉變為球臺壓板屈曲破壞，節點極限承載力對球臺壁厚的敏感程度大大降低.

圖10 節點承載力與球臺壁厚關系曲線Fig.10 Relationship curve between joint bearing capacity and table wall thickness

對比兩節點的承載能力可發現，橢球型節點的極限承載力整體要高于分體球型節點8%～15%.究其原因，是因為分體球型節點球臺主要承受螺栓球傳遞的軸向力，節點承載能力由球臺軸向抗拉承載力和球臺壓板承載力兩者中的較小值決定；而橢球型節點球臺主要受橢球傳遞的橫向力，球臺與球臺壓板的極限承載能力共同決定了節點的承載能力.

5 結論

1）分體球型節點的破壞模式為球臺材料強度破壞與球臺壓板屈曲破壞.橢球型節點的破壞模式表現為球臺壓板撕裂破壞與高強螺栓螺紋破壞.

2）由腹桿荷載-變形關系曲線得：在相同壁厚條件下，橢球型節點的彈性階段更長，承載能力更強.且曲線在彈性階段時，球臺壁厚由6 mm 增長至10 mm 時，橢球型節點的整體剛度顯著增強，但對分體球型節點整體剛度提升不大.

3）由節點等效應力分布情況得：相對于橢球型節點，分體球型節點應力分布更為均勻，應力極差更小，材料利用率更高.隨著球臺壁厚的增長，分體球型節點球臺等效應力水平下降的同時球臺壓板等效應力顯著上升.橢球型節點球臺及球臺壓板的等效應力水平均有較大水平降低.

4）由節點破壞模式結合有限元分析可知，節點構造形式的不同導致球臺受力模式存在差異，使得橢球型節點的極限承載力高于分體球型節點5%～18%.

5）采用有限元分析軟件對球臺壁厚進行參數擴展，得出球臺壁厚對兩種節點承載能力的影響規律.結果表明：當分體球型節點球臺壁厚增長至7 mm，橢球型節點球臺壁厚增長至9 mm 時，兩種節點的極限承載力對球臺壁厚的敏感度大大降低，研究結果可為工程設計提供參考.