松散巖堆細-宏觀強度關系與圍巖壓力

陳志敏 ，劉耀輝 ，郭利民 ，李寧 ，王壹敏

（1.蘭州交通大學 土木工程學院，甘肅 蘭州 730070；2.中鐵第一勘察設計院集團有限公司，陜西 西安 710043；3.道橋工程災害防治技術國家地方聯合工程實驗室（蘭州交通大學），甘肅 蘭州 730070）

受青藏高原構造運動影響，中國西南某高海拔地交界地帶山高谷深且地質運動活躍，為大孔隙率松散巖堆的形成創造了合適的自然條件.

松散巖堆是巖塊與土體的混合巖土體，巖塊和土顆粒的混合特征與松散巖堆的形成條件有直接關系，巖塊堆積具有一定特征，堆積體存在時間越短，其架空越明顯，土體填充越少，巖堆越松散［1-3］.國內外學者對此類大孔隙率松散巖堆做了許多試驗研究.Vallejo 等［4］研究了砂石-黏土混合材料的不同含量對抗剪強度影響；龔超凡等［5］研究了試樣高度對粗顆粒土抗剪強度的影響；荀曉慧等［6］根據能量守恒原理和Mohr-Coulomb 強度準則，推導了能量演化與強度參數的關系等；對于密實硬巖巖堆，壓實度主要取決于巖塊間的摩擦阻力，巖塊壓碎引起的變形量很小；內摩擦角隨周圍壓力的增大呈非線性，壓實硬巖巖堆的應力-應變關系近似彈性應變軟化型［7-9］.上述研究都是基于連續介質力學假定進行宏觀層面的物理力學性質研究.巖塊單元相對隧道洞室的大小程度使得其既不能應用巖石力學的方法，也不能應用經典土力學方法解決圍巖穩定問題.松散巖堆與一般巖土體的最大區別在于其相對大小和非連續性，不符合以上兩種方法的連續均勻性假設.

經典土力學解決了大量實際問題，為注重機理研究的顆粒材料力學提供了驗證依據，并指導顆粒材料力學的研究更加接近實際工程，因此土力學與顆粒材料力學有緊密的聯系，無黏性砂土的剪脹性研究更是促進了巖土顆粒力學的發展［10-11］.例如：有效應力可以用土顆粒的浮力定律來解釋，達西滲流定律可以解釋為巖土顆粒間的孔隙流體平衡和顆粒骨架對流體的阻力作用的綜合描述，進一步有飽和土力學的孔壓系數的微觀解釋以及巖土本身的微觀結構都蘊含著深刻而嚴格的顆粒材料力學問題.隨著土力學的發展，土力學研究者越來越重視巖土微觀結構作用.宏-微觀參數對應關系是顆粒力學的一個基本問題，土體微觀結構測試［12］、顆粒間接觸測試［13］及DEM 模型［14］更是推動了土體宏微觀研究的發展.常在［15］、劉海濤等［16］研究了砂土宏觀抗剪強度與顆粒間摩擦強度之間的相似關系；鞏師林等［17］改進了DDA 計算方法中的塊體變形問題；康馨等［18］引入修正的三維形狀系數S，研究了不同砂顆粒對其相關物理量的影響；曹文貴等［19］探討了在空隙變化影響下巖石微觀應力和變形與其宏觀應力和變形之間的關系；蔡國慶等［20］依托PFC3D 中的黏結模型建立了非飽和土體顆粒間黏結強度的宏-細觀關系.上述研究多是從宏-微觀角度研究土體的強度特性，對于松散巖塊的局部強度研究仍有不足.與傳統土力學材料不同的是，松散巖堆在破壞時與其荷載方向有很大關系.巖塊材料通過接觸力鏈，少數顆粒承擔了大部分力；在純剪和雙向壓縮狀態下，接觸力方向差異較大［21-22］.因此松散巖堆局部強度對工程而言同樣有重要意義.顆粒粒徑和試樣尺寸不同時，強度相差很大，若巖堆材料數量足夠大，則宏觀峰值強度趨于穩定［23-24］，而局部強度特征不能體現.

松散巖堆是典型的顆粒材料，在隧道進口和出洞段的松散巖堆的圍巖變形問題目前仍是隧道工程中一個尚未明確的重要問題.為了研究松散巖堆的強度和圍巖穩定，本文從顆粒材料力學對致密砂土的力學分析出發，來研究松散巖堆的細觀巖塊單元與宏觀強度的密切關系.

1 松散巖堆細觀咬合關系模型

1.1 經典應力剪脹關系

Rowe［11］在20 世紀60 年代提出了顆粒材料的應力剪脹關系，并提出了滑裂面的剪切滑移分析模型.模型建立在密實砂土三軸試驗狀態的基礎上，模型假設試樣為兩塊剛性楔塊，楔塊沿剪切面發生滑移，滑移面與最小主應力σ3方向夾角為α，而顆粒材料的滑移面在咬合作用下呈現鋸齒狀，鋸齒面p與最大主應力σ1方向夾角為β.

Rowe 認為鋸齒面相互滑動過程中體積增大，可以解釋顆粒材料的剪脹性，如圖1 所示.繼而通過平衡條件和變形協調條件得出了應力剪脹關系式，見式（1）.

圖1 Rowe剪切滑移分析模型Fig.1 Rowe shear slip analysis model

式中：σ1和σ3分別為最大和最小主應力；εv和ε1分別為體積應變和軸向應變；φμ是顆粒間摩擦角.

Rowe根據最小能比原則，得到：

從而得到Rowe應力剪脹關系：

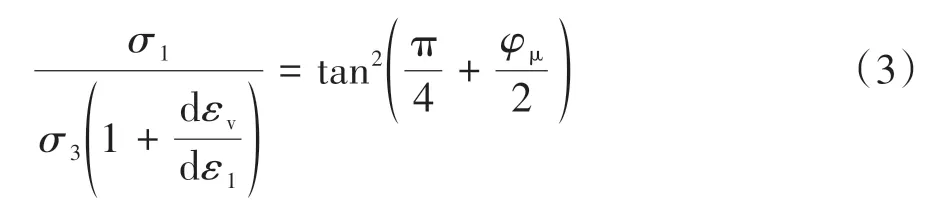
該公式在顆粒材料密實狀態下吻合較好，松散狀態時，Rowe進行了修正，用松散顆粒材料摩擦角φf代替φμ（φμ≤φf≤φcv），φcv是三軸試驗中的臨界摩擦角.

隨后，Josselin［25］利用摩擦定律對Rowe采用的最小能比原理進行了證明，其力學模型如圖2 所示.模型中α是下鋸齒面與最小主應力方向的夾角，β是上鋸齒面與最大主應力方向的夾角，θ為鋸齒面和滑移面的夾角，它們三者有著一定的關系，即θ=α+β-π/2，n為鋸齒面的法線方向，F為鋸齒面上的作用合力，ω為力F與法線方向n的夾角.

圖2 Josselin剪切滑移分析模型Fig.2 Josselin shear slip analysis model

上述模型假設的前提是都存在鋸齒狀剪切滑移平面，且發生了剪脹.大量顆粒材料三軸試驗表明，在密實狀態下該應力剪脹關系公式與應力應變關系有很好的契合度，但在解釋松散顆粒材料狀態下的應力應變關系時較為困難.松散顆粒材料的三軸試驗變形破壞結果并非存在鋸齒狀滑移平面，松散狀態下留有較大的孔隙率可以有效地緩解或者抵消剪脹作用，松散顆粒材料更容易發生局部應力應變.基于此，要進一步研究大孔隙率松散巖堆強度關系則需進一步建立細觀模型.

1.2 松散巖堆細觀咬合關系模型建立

松散巖堆有一定的寬泛的顆粒級配，一般只受到重力荷載的堆積作用，其密實度較小，而且有較大的孔隙率，在隧道工程中的圍巖力學行為主要是由于卸載引起的，與應力剪脹關系有所區別，因此其細觀的咬合作用有待進一步分析研究.

此外，上述應力剪脹關系中的體積應變與軸向應變在實際工程中現場測量較為困難.松散巖堆粒徑較大，開展現場試驗較為困難，通過運用土力學和顆粒材料力學來研究松散巖堆細觀巖塊單元間的力學機制與宏觀強度的關系是一個較好的解決辦法.通過較為簡單的物理力學參數來得到松散巖堆的強度，從而方便實際工程中的運用.

松散巖堆主要受自重應力影響，結構較細粒土更加簡單，其破壞過程主要是堆積單元巖塊的物理運動.假設松散巖堆的破壞過程沒有單個巖塊的擠壓碎裂，可以簡單地認為，每個基本巖塊單元為剛體，松散巖堆在類彈性階段的強度主要依靠巖塊單元的咬合作用，而巖塊單元間的咬合主要是來源于特殊的摩擦機制.

松散巖堆有著非線性特征和應力應變局部化、跨越固體和液體的類固-液轉變行為.與顆粒力學有所區別的是，松散巖堆是一種宏觀的力學行為，松散巖堆變形有著不可逆性.在上面模型的基礎上，建立細觀狀態下的松散巖堆的平面咬合模型，如圖3所示.

圖3 咬合作用示意圖Fig.3 Schematic diagram of occlusion

由于大部分自然形成的巖塊表面往往是坑洼不平的，其接觸必定是較小面積與較大面積間的接觸，為了突出該特點，松散巖堆的變形模式是點-面接觸作用，以某一巖塊作為絕對靜止的對象，和它咬合的其他兩塊巖塊作相對運動，其運動軌跡是點-面接觸模式下，沿巖塊單元接觸面的滑移和以點為圓心的轉動.在接觸變形的情況下，變形之前，巖塊滑移面與豎向夾角為β，發生小變形后，巖塊發生滑移面偏移，由于巖塊相對旋轉偏移角度為θ，滑移面與水平方向夾角為α，它們三者之間滿足下列關系：

2 松散巖堆咬合關系與宏觀強度規律的關系

接觸點合力方向與滑移面法線方向成夾角ω，而巖塊單元間的摩擦角設為φμ，依據摩擦定律有：

當ω＜φμ時，兩巖塊單元有滑動趨勢，但不會發生相對滑動；

當ω=φμ時，兩巖塊單元間滑動趨勢達到滑動摩擦力，可以發生相對滑動；

當ω＞φμ時，在松散巖堆破壞形式下，認為巖堆內部巖塊單元運動速度很小，不考慮加速度，兩巖塊單元間的合力超過最大滑動摩擦力，這種情況不會出現.

同樣地，依然假設松散巖堆受力狀態為三軸應力狀態，內部巖塊單元咬合機理如圖3 所示，在笛卡兒坐標系下進行方向標定，以豎向或軸向為y軸，而x軸和z軸構成水平的平面坐標，巖堆三軸試樣在x、y、z方向上的有效應力分別可以表示為σ′1、σ′2、σ′3，并且三軸狀態下應力關系為σ′1＞σ′2=σ′3.

在對松散巖堆體相似材料做三軸試驗之后發現，松散巖堆變形以鼓狀變形為主，其變形如圖4 所示.之所以出現膨脹變形是由于較大的孔隙率提供了軸向壓縮變形空間，在松散巖堆壓縮變形的同時，由于咬合作用產生圍向膨脹變形，在這個過程中巖塊單元間的咬合作用主要來源是特殊機制下的摩擦力，對于摩擦因數基本一致的松散巖堆，可以認為內部巖塊單元間的接觸力大小相等.上述模型中假設在松散巖堆發生變形時，水平方向約束條件不變，巖塊單元間合力方向與水平方向夾角為ω+β，由圖3中關系可得到：

圖4 巖堆相似材料三軸試驗試樣變形特征Fig.4 Deformation characteristics of triaxial test specimens of similar materials in rock piles

式中：Fy′為巖塊單元間作用力的豎向分力；Fx′為巖塊單元間作用力的水平方向分力.

松散巖堆咬合作用下的變形，主要是巖塊單元的相對平動和轉動，這兩種方式都可以占據主導地位，主要取決于巖塊單元間的摩擦因數和比密實度.但無論哪種方式占據主導，松散巖堆剪脹效應的實質是由宏觀狀態下軸向和橫向變形引起的，因此在松散狀態下巖塊單元相對轉動引起的體積變化，可以轉化為巖塊單元間接觸面上的位移.

無論是平移，還是轉動，對于某個巖塊單元來說位移是由于和其配位接觸的其他巖塊單元相互作用引起的，因此它的運動是協調的，沿著點-面接觸相對滑動一段極小位移Δu′則可以代表這個巖塊單元的剪脹變形量，uy′是巖塊單元的豎向相對位移，ux′是巖塊單元水平方向相對位移，滿足矢量關系：

由上述的幾何關系可以得到：

巖塊單元在外力作用條件下消耗一定能量，主要消耗對象是巖塊單元間的摩擦作用.由于巖土體的變形可以認為是緩慢的或者靜止的，因此忽略巖塊單元的滑動動量和轉動慣量條件下，定義軸向和橫向變形所消耗的能量比為：

由式（8）可知，能量比E隨著ω的增大而增大，隨著β的增大而減小.能量比E可以通過宏觀的外力做功獲取，而巖堆內部巖塊單元間滑移面與豎向夾角β，由于各個巖塊單元間咬合過程中的滑移面角度不同，可以看作自變量.而在一定的外界荷載和約束條件下，接觸點合力方向與水平方向所成夾角為ω+β，因此ω可作為因變量，進而得到：

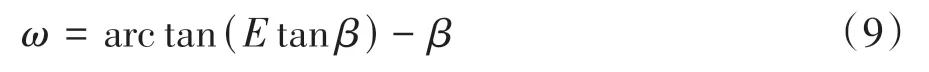
對式（9）求導，利用ω最大值條件?ω/?β=0，來求得所對應自變量β的值：

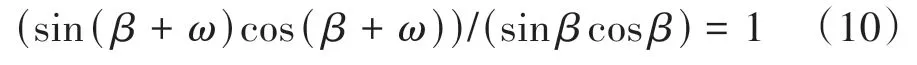
利用三角函數倍角變換以及β、ω的值域得：

進一步對兩者關系進行分析，對原式求二階導數，將該值代入得到：

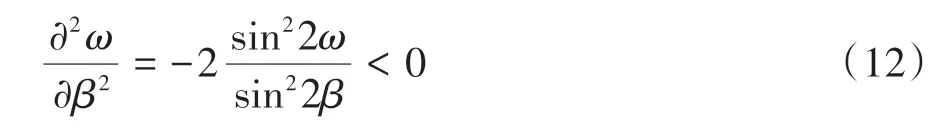
由此可知，該值是一個極大值.ω的值域為（0，φμ）.當巖堆發生變形時，內部巖塊單元間ω達到最大值；當ω+β為一個定值時，β越大則能量比E越小.由上述求導可知，ω是關于β的增函數，由此可知當ω=φμ作為極大值時，β也最大，因此能量比E也越小，因此得到：

實際工程中，巖塊單元間通常不是嚴格意義上的點-面的接觸，還需要考慮到接觸面積ΔA，Ax′和Ay′分別是橫向和豎向的接觸面積，根據幾何關系，可以得到：

根據應力和力的關系，將接觸面積比代入，可以得到巖塊單元間接觸極限應力比值，若將松散巖堆三軸應力狀態下的荷載在巖堆內部平均化，則可以得到細觀咬合模型同宏觀外荷載的關系：

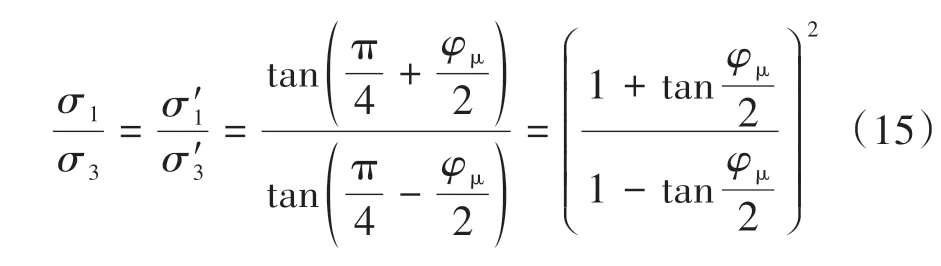
值得一提的是，這里的外荷載與巖堆內部應力并不是相等關系，還與巖塊單元的孔隙率和實際接觸面積等有關.然而可以簡單地認為，豎向和橫向的內部結構一致，因此外荷載與巖堆內部應力比值大小是相等的.由式（15）可知，松散巖堆細觀摩擦角對宏觀強度有較大影響.

3 松散巖堆隧道圍巖力學分析

3.1 普氏理論松散巖堆圍巖應力拱

圍巖壓力的確定對隧道設計和圍巖穩定性分析有重要意義，圍巖壓力可以通過直接測量、經驗、理論估算等方法確定.較早的理論只考慮單因素下的圍巖壓力計算，主要有普氏理論和應力傳遞法等，隨后出現了雙指標分級、巴頓巖體質量（Q）分級、BQ 分級法、專家系統法和模糊信息評價法等多因素圍巖壓力計算方法，目前我國的圍巖壓力計算方法是根據以BQ分級法為基礎的經驗法制定的.

松散巖堆可看作是巖體破壞后的坡體或者以堆積體形式存在的，自然堆積形成一定高度，除重力場方向的地基承載力以外，必須有一定的側向約束，才能保證其具有一定高度.巖堆內部接觸力鏈不是豎向傳遞的，而是水平力和豎向力的合力.假設地基是絕對光滑地面，巖堆則不會形成坡體.為方便研究，假定巖堆接觸力鏈構成平面力鏈網，可以得到滑移面網格分布如圖5 所示，力鏈網的拐點是虛構的，是假設巖塊單元的平面配位數為4，通過延伸滑移面得到的.

松散巖堆在小變形階段保持穩定狀態，也就是應力應變曲線類彈性變化階段.滑移面、巖塊在點-面接觸下的內部應力路徑等如圖5 所示，將咬合模型中的各巖塊單元的滑移面延伸相交，組成網格，各網格內部代表不同形狀的巖塊單元.當巖塊單元間達到其最大摩擦角ω=φμ時，巖塊單元間發生的位移很小，滑移面角度β=π/4-φμ/2，咬合作用的偏轉角θ=0，那么由式θ=α+β-π/2，可得滑移面與最小主應力的夾角α為：

圖5 松散巖堆滑移面網格分布Fig.5 Grid distribution of slip surface of loose rock pile

當隧道開挖后，巖堆內部發生應力重分布，一定范圍內的巖塊單元沿臨空面產生位移，形成松弛.由于側向邊界約束的作用，形成一定的拱效應.當滿足式（16）時，圍巖可以形成自穩的應力拱.

為了求得自穩的應力拱高度內的圍巖壓力，必須確定隧道洞頂到應力拱線的最大距離h.以自然平衡拱軸線的頂端為坐標原點，建立笛卡兒坐標系，水平向左為x軸正方向，豎直向下為y軸正方向，自然平衡拱軸線圖如圖6所示.

應力拱軸線拱腳處松散巖堆應滿足深度條件：

式中：γ為松散巖堆宏觀重度；H為平衡應力拱拱腳處埋深；T為應力拱軸線拱頂處水平推力.

拱軸線與原點相交，在原點o（0，0）處取一微段，從細觀角度分析如圖7 所示.普氏理論將計算模型簡化，認為豎向壓力q是拱軸線上部巖體的自重所產生的均布荷載，且圖7 實質上是圖6 拱軸線上的微段，當x方向上取一微段dx時，拱軸線上對應為m點，m點彎矩應為均布荷載的合力G乘合力作用點到m點的距離（y=dy時所對應的dx的一半）.拱軸線是圍巖是否塌落的分界線，故在拱軸線上巖體不能承受拉應力，當y=dy時，豎向荷載G和水平推力t到拱軸線上m點的彎矩作用差值應為0，從而得到式（18）.

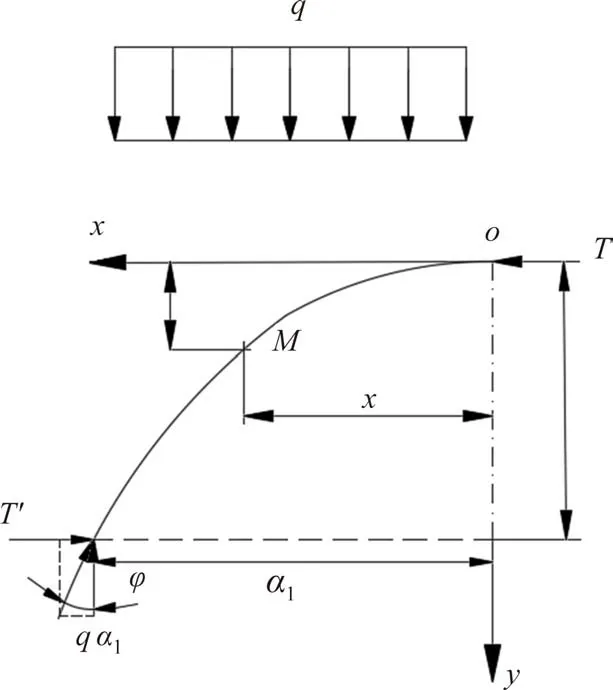
圖6 自然平衡拱計算圖Fig.6 Calculation diagram of natural balance arch

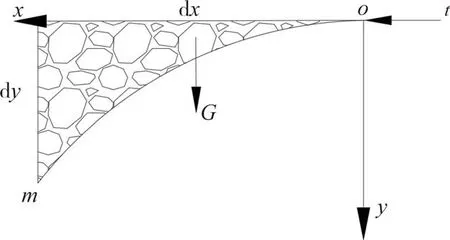
圖7 拱軸線微分示意圖Fig.7 Differential schematic diagram of arch axis

式中：G為微段拱軸線上部巖體的自重荷載，即G=qa；t為平衡應力拱拱頂截面的水平推力；dx、dy分別為o點的x、y軸增量值.

在拱軸線任意點處，該微段受外荷載作用可看作是與三軸應力狀態一致，則根據松散巖堆宏觀外荷載與細觀咬合強度關系可得：

由式（18）和式（19）可得到y軸的增量dy與松散巖堆細觀強度關系為：

求解式（20）所示微分方程即可得到應力拱軸線在笛卡兒坐標下的解析式：

式中：C為常數，受多種因素影響，主要與松散巖堆的巖塊單元與隧道洞徑的比值、巖堆體內摩擦角φμ有關，粒徑小至一定值時，所需最大高度y為無限大.

由式（21）可知，自然平衡拱軸線為二次拋物線，其應力平衡條件為二次項，應力拱高度與咬合強度關系呈正相關.

當應力拱的跨度達到a1時，即可得到隧道洞頂到應力拱線的最大距離h為：

式中：a1為應力拱軸線的計算水平距離，可由α與隧道斷面高度Ht的三角函數關系得到：

3.2 基于細-宏觀強度關系的松散巖堆圍巖壓力

普氏理論認為：作用在硐室頂部的圍巖壓力僅為拱內巖體的自重.但普氏理論僅僅是在宏觀層面給出了圍巖壓力的計算方法，而對于松散巖堆體隧道，洞頂所受圍巖壓力應考慮巖堆體細-宏觀強度關系，因此認為對于硐室頂部的圍巖壓力仍然可以用普氏理論去計算，但需對其做出修正，隧道所受圍巖壓力示意圖如圖8 所示.結合松散巖堆細觀咬合模型與宏觀外荷載之間的關系，由式（15）和式（22）即可得到大孔隙率巨型松散巖堆體考慮了細-宏觀強度關系的圍巖壓力計算公式如式（24）所示.

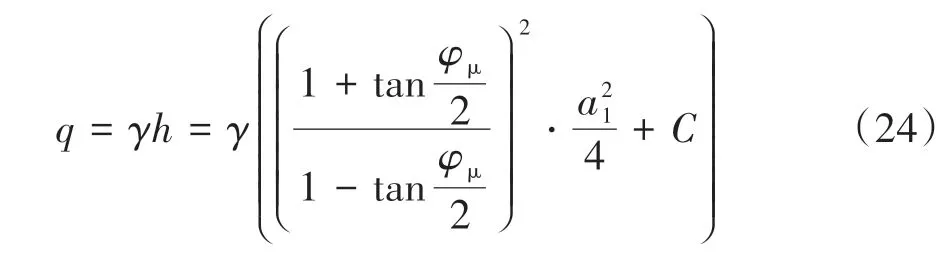
圖8 松散巖堆隧道細-宏觀圍巖壓力示例圖Fig.8 Example diagram of fine-macroscopic surrounding rock pressure of loose rock pile tunnel

隧道硐室的側向圍巖壓力，同樣考慮松散巖堆體的咬合作用機制及細-宏觀強度關系，因此同樣對宏觀層面普氏圍巖側向壓力理論值做出修正：

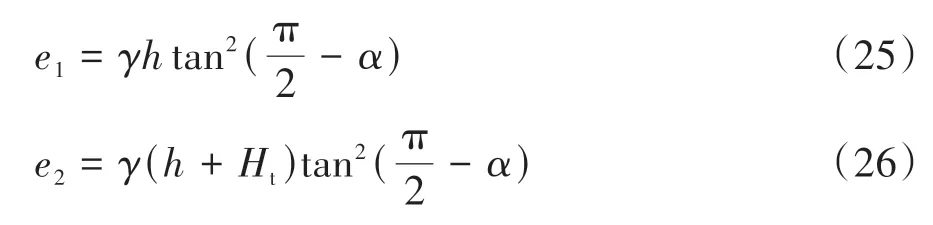
聯立式（15）（16）（22）（25）（26）可得松散巖堆隧道硐室側向圍巖壓力：

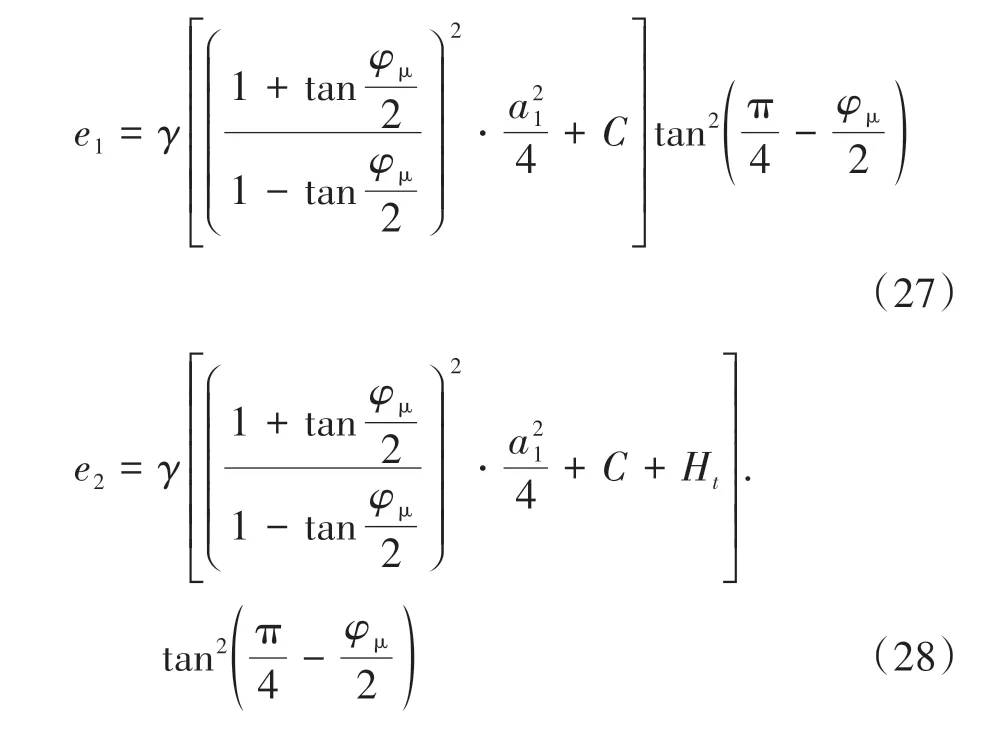
由此可見，松散巖堆體隧道的圍巖壓力無論是豎向壓力還是側向壓力與咬合強度的關系均為正相關，圍巖壓力均受到應力拱軸線的計算水平距離a1與巖塊單元間的摩擦角φμ的共同影響.

3.3 松散巖堆隧道圍巖壓力計算實例

中國西南某鐵路隧道進出口段分布有較大規模的巖堆體，主要以碎石為主，厚度10～50 m 不等，塊徑多介于0.5～2 m，最大塊徑達到5 m，在自然狀態下穩定性較好.巖堆對隧道主體工程影響較大，施工會影響巖堆的穩定性，存在局部失穩風險.依托該隧道工程建設，采用修正的細-宏觀普氏理論圍巖壓力計算公式，對隧道圍巖壓力進行計算，并與太沙基理論圍巖壓力及《鐵路隧道設計規范》（TB 10003—2016）［26］（以下簡稱規范）圍巖壓力計算結果對比，計算中各參數取值見表1，圍巖壓力計算結果見表2.其中，在太沙基理論計算中采用朗金公式計算其側向圍巖壓力，常數C的取值可參考如式（29）所示經驗公式計算，但后續仍需大量數據進行修正：

表1 中國西南某鐵路隧道圍巖壓力計算參數表Tab.1 Calculation parameters of surrounding rock pressure of a railway tunnel in southwest China

式中：d為巖體粒徑，m.

為方便對比，考慮到普氏理論及規范算法中側向圍巖壓力均呈線性變化，因此取平均值與其余結果比較.由表2 可知：修正后的普氏理論比一般普氏理論計算結果大，差值約28 kPa，局部強度對整體圍巖壓力的影響不可忽略，說明本文所提出的計算公式是合理的、可應用的，但由于普氏系數的計算有人為經驗因素影響，修正后的普氏理論則嚴格受到內摩擦角及滑移面與水平面夾角α的影響，更為科學嚴謹；修正的普氏理論在豎向圍巖壓力計算中比太沙基理論和規范方法略大，除規范深埋算法的結果之外，差值均在30 kPa 以內，這是由于太沙基理論和規范算法中僅僅是將豎向圍巖壓力在宏觀上整體簡化為均布荷載，并沒有考慮到巖體內部由于相互咬合而造成的細觀局部強度帶來的影響，而修正的普氏理論將巖體各部分細觀局部強度同樣用宏觀角度均布作用于硐室上方.值得注意的是，規范算法中無限埋深計算方法計算結果出現較大誤差，這是由于規范算法在計算過程中僅僅是考慮到硐室上方圍巖的自重，忽略了滑移面造成隧道跨度增大的影響，故該方法計算豎向壓力結果明顯小于其余兩種方法，使得其側向圍巖壓力同樣偏小.對比側向圍巖壓力后發現，修正普氏理論計算結果均與其余兩種方法有較大差距，差值在80 kPa 左右.究其原因，認為：算例圍巖是巨型大孔隙率松散巖堆體，其咬合模型為點-面接觸，在受到荷載作用后，巖堆巖塊內部產生位移使得其找到新的平衡位置，使得巖塊間接觸更為緊扣，造成部分圍巖壓力向圍巖方向傳遞，從而使硐室側向圍巖壓力減小.

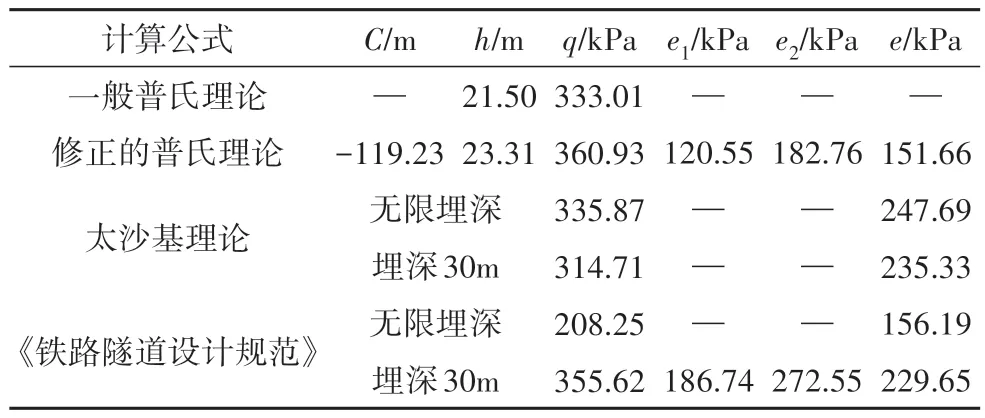
表2 中國西南某鐵路隧道圍巖壓力對照表Tab.2 Comparison table of surrounding rock pressure of a railway tunnel in southwest China

綜上所述，基于細-宏觀強度修正的普氏理論圍巖壓力公式更適用于有較大埋深的松散巖體隧道.

4 結論與展望

本文從致密砂的應力剪脹關系式出發，通過分析得出了松散巖堆的細觀咬合模型，推導出由巖堆內部巖塊單元的摩擦角主導的宏觀強度關系式.從適合破碎圍巖的普氏理論出發，結合巖堆細觀強度公式，得出了松散巖堆自然平衡拱軸線的計算方法，從而從細-宏觀角度修正了圍巖壓力計算公式.主要結論如下：

1）松散巖堆接觸模式為點-面接觸，其運動軌跡是沿接觸面的滑移和以點為圓心的轉動；巖塊內摩擦角對宏觀強度有重要影響，內摩擦角越大，宏觀強度越高.

2）應力拱軸線高度h受細-宏觀強度關系σ′1/σ′3與滑移面與水平面夾角α共同影響，巖堆細觀局部強度對整體圍巖壓力的影響不可忽略.

3）針對松散巖堆細-宏觀力學特性，對普氏理論進行了修正.中國西南某鐵路隧道計算結果表明，修正普氏理論結果稍大，體現了松散巖堆隧道的細-宏觀力學特性，表明了修正普氏理論的可行性與實用性.

4）修正的圍巖壓力公式更適用于有較大埋深的松散圍巖隧道.后續研究重點將是運用大量數據修正常數C的擬合函數以及在普氏理論計算模型推導過程中求m點彎矩時力臂的取值問題，普氏理論模型仍有待繼續修正、細化.