高壓電器設備包裝材料優選研究

高嶺，王璞，伊朋

高壓電器設備包裝材料優選研究

高嶺，王璞，伊朋

（西安西電開關電氣有限公司，西安 710077）

目的 實現高壓電器設備包裝材料的優選，提高包裝材料選擇的一致性和經濟型，降低制造成本。方法 建立一種多目標材料選擇優選模型，包括包裝承載力、包裝可靠性、包裝成本、資源消耗、包裝綠色性等5個優化目標，使用組合隸屬度函數構建評價指標集，運用灰關聯法與基于可能度排序算法的模糊層次分析法相結合的方法，實現材料優選。結果 候選材料的關聯系數分別為0.745、0.606、0.669、0.749。結論 關聯程度最大的包裝材料為最終優選包裝材料。

高壓電器設備；包裝材料優選；灰關聯法；三角模糊數；層次分析法

高壓電器設備是關系國計民生的基礎性設施設備，一般安裝在較為偏僻的地區，具有體積大、質量大、運輸困難等特點，包裝材料直接影響高壓電器設備運輸的可靠性和綜合成本，對產品順利投入使用至關重要。在傳統的包裝設計中，企業通常依靠經驗進行包裝材料的選擇，技術文件也依照經驗進行編制，但自身經驗存在局限性，隨著新材料不斷涌入，還需考慮成本控制、綠色制造等多種因素，以及各個影響因素的相互制約，傳統經驗具有滯后性和片面性。電器設備包裝材料的評價選擇在行業間尚屬空白，因此建立合適的包裝材料選擇評價體系，綜合各種影響因素，選擇最優的包裝材料具有重要意義。

高壓電器設備包裝材料的優選是一個多目標、多約束的復雜優化問題，文中在綜合分析上述方法的優缺點的基礎上，提出利用灰關聯分析法和基于三角模糊數的層次分析法相結合的評價方法，根據不同的評價因素，采用組合隸屬度函數，使用基于可能度的排序算法確定權重，實現對包裝材料進行選擇，并使用實例驗證了該方法的有效性，這種方法準確、可靠，填補了高壓電器領域包裝材料選擇的空白。

1 灰關聯分析法和三角模糊數

1.1 灰色關聯分析法

1）建立評價指標矩陣。將評價指標無量綱化以后建立評價矩陣為：

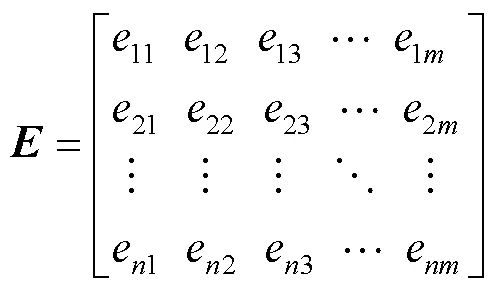
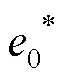
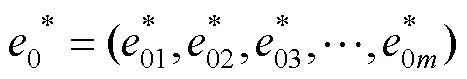
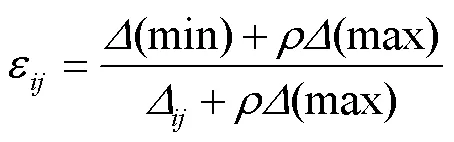
4）計算關聯系數矩陣。關聯系數矩陣的計算公式為：

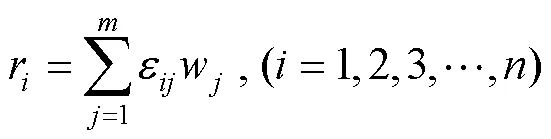
最后通過對關聯系數進行排序，可以選擇出最優包裝材料。

1.2 三角模糊數

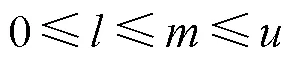
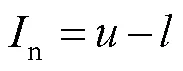
若n值越大，則評判越不清晰。

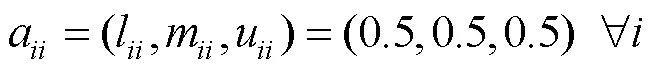
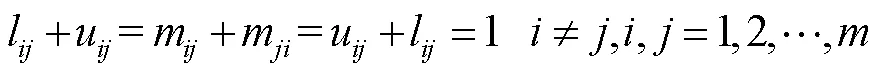
則稱矩陣為模糊互補判斷矩陣。

2 包裝材料優選模型的建立

2.1 包裝材料優選綜合評價指標體系的建立

對產品包裝材料進行最優選擇時，應首先建立包裝材料選擇的評價體系，目標層即為最優包裝材料。在包裝設計過程中，材料的選擇不僅要滿足強度要求及經濟性要求，還要充分考慮其環保性和綠色性，因此，評價體系的優化指標層為承載力B、包裝可靠性S、包裝成本C、資源消耗R、環境影響E。每種材料有13個影響因素，作為影響因素層，共同構成了包裝材料選擇的層次分析模型，見圖1。

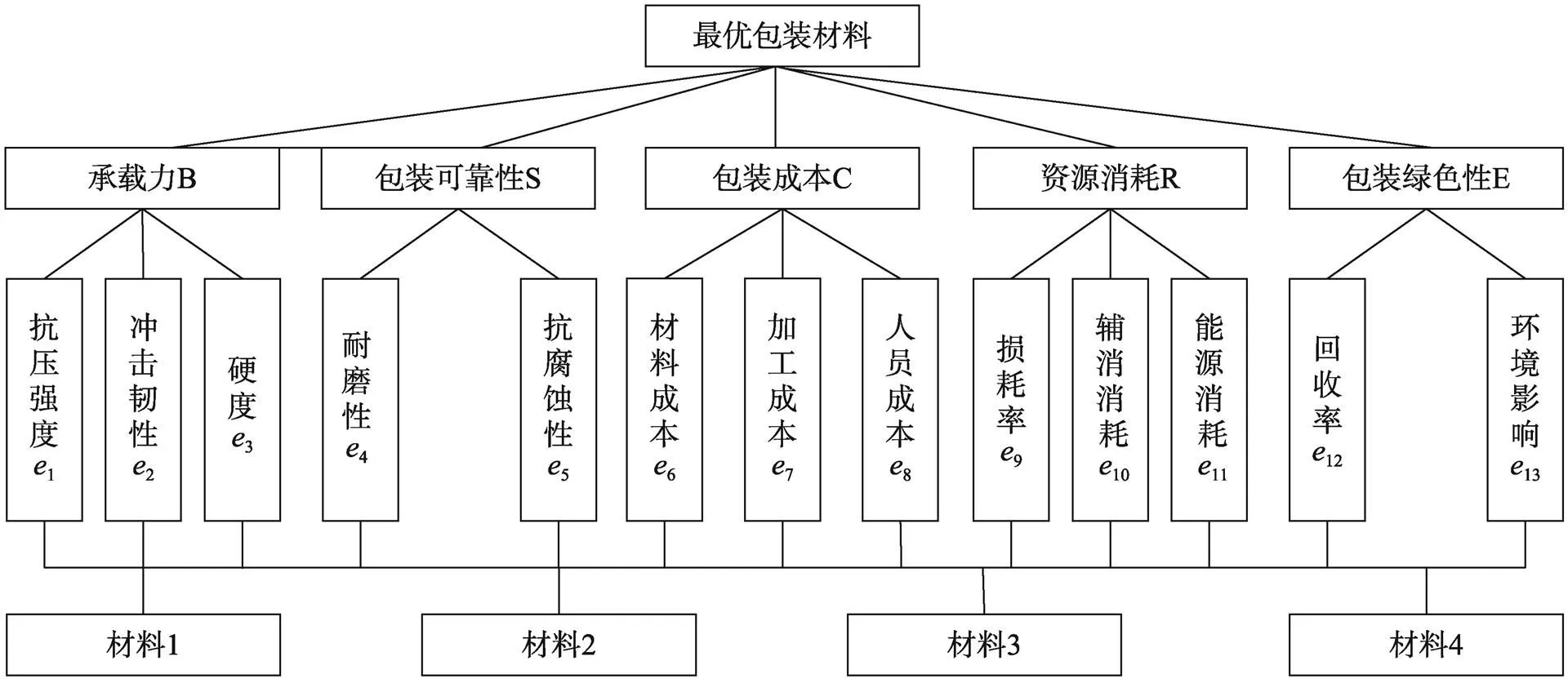
圖1 包裝箱材料優選評價體系

2.2 無量綱評價指標集的確定

2.1節共確定了13個影響因素，各個影響因素單位不一致，其中影響因素4、5、13為定性描述類因素，無法直接比較。需要13個影響因素轉換為無量綱的數值進行比較。若采用單一的隸屬度計算方法會導致評價的可信度降低，對于不同的決策因素，需采用不同的隸屬度計算方法。

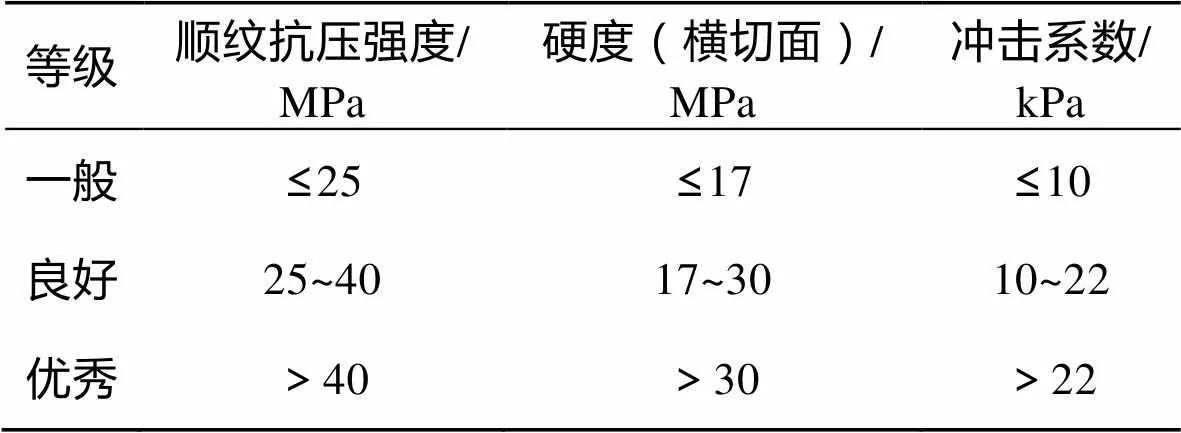
表1 包裝材料承載力等級劃分

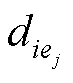
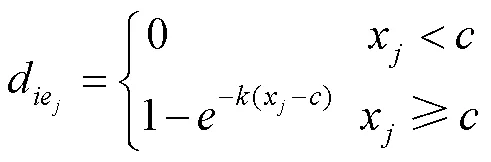
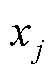
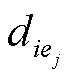
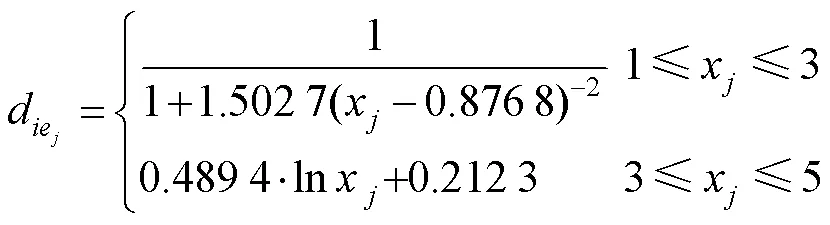
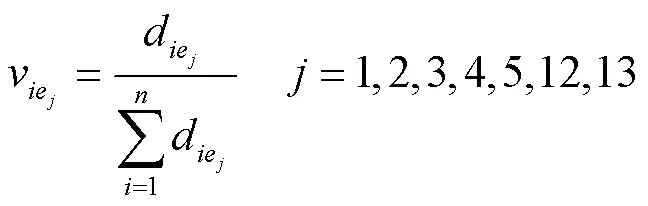
對于越小越好型的影響因素，采用以下統一化計算公式：

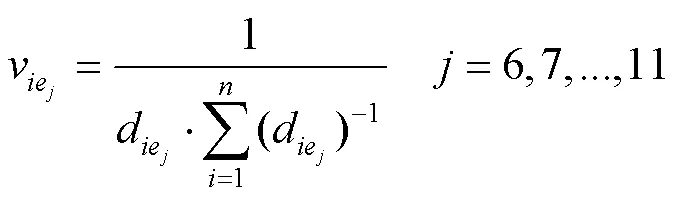
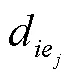
2.3 包裝材料優選評價指標權重的確定

模糊層次分析法（FAHP）是20世紀70年代首次提出的一種定性與定量相結合的系統分析方法[18]，該方法可量化評價指標，能有效分析目標各層次之間的關系，在各個領域得到廣泛應用。通過基于三角模糊數的層次分析法，計算各影響因素權重。

FAHP實現決策因素權重分配的步驟如下。

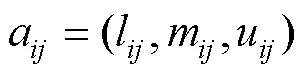
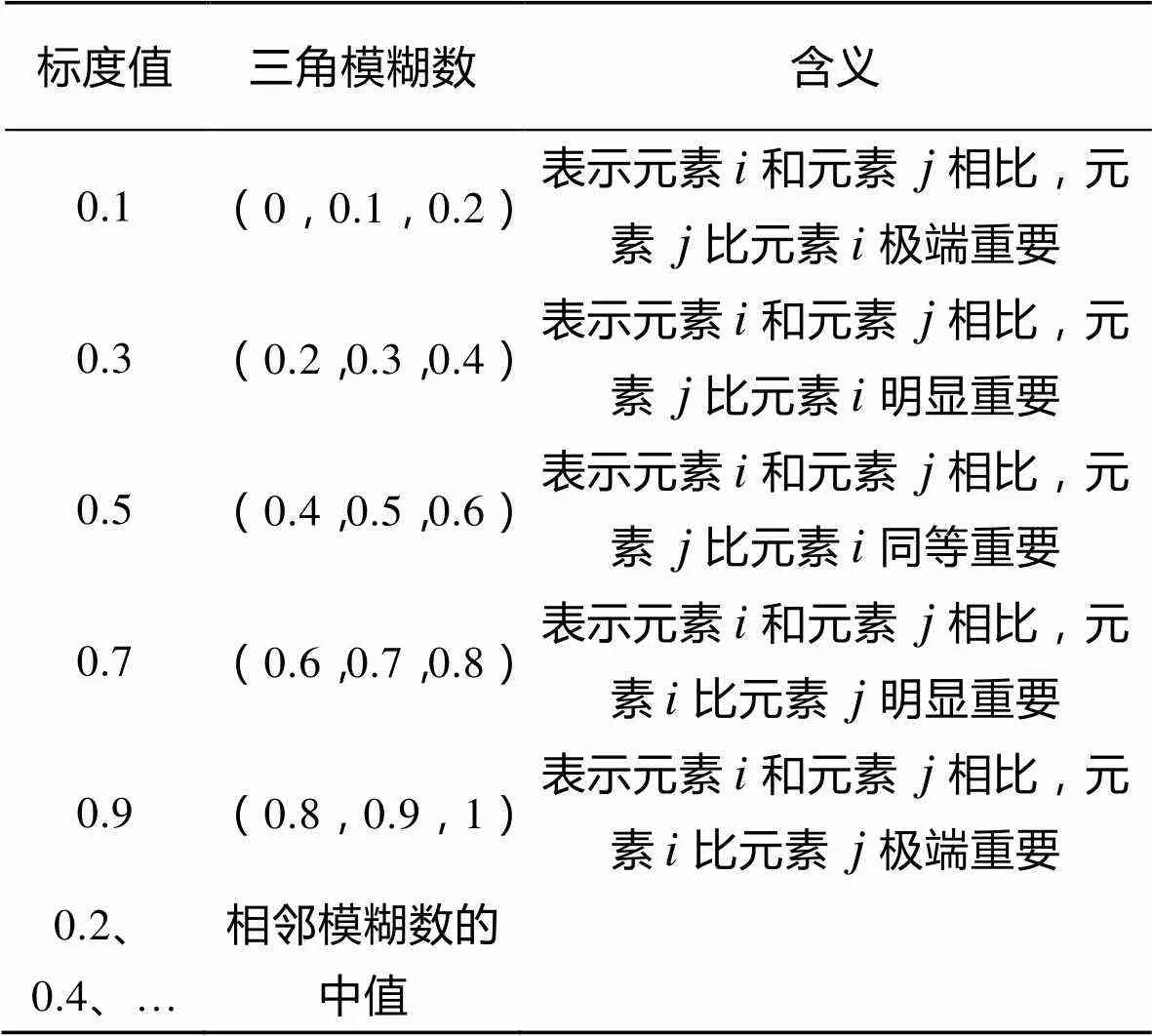
表2 模糊標度值及其含義

2）對模糊矩陣進行排序。基于三角模糊數的權重計算方法包括加性一致排序法[19]、乘性一致性排序法[20-22]、可能度排序方法[23-24]等。文中使用改進的基于可能度的排序算法，可以對不同影響因素進行反復比較，最終確定一個能反應決策者整體判斷的權重排序，具體步驟如下。

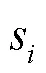
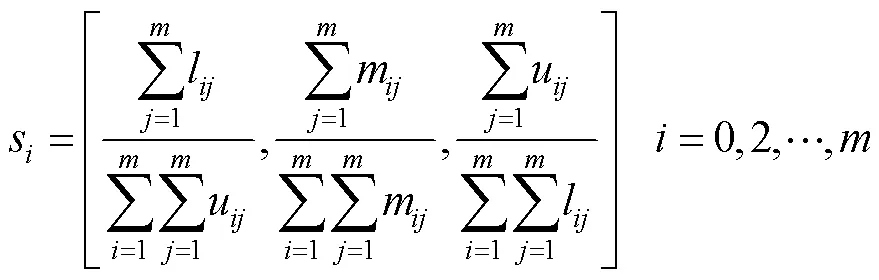
通過兩兩比較三角模糊數權重s，計算可能度p=(s＞s),(,=1,2,…,)，構建判斷矩陣=(p)×m,=1,2,…,。

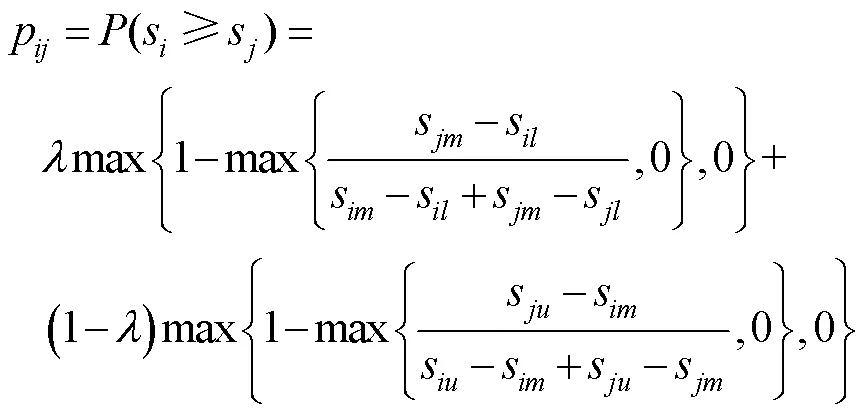
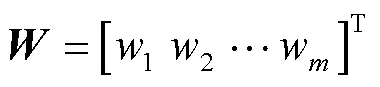
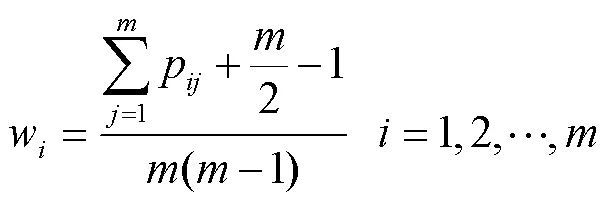
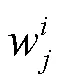
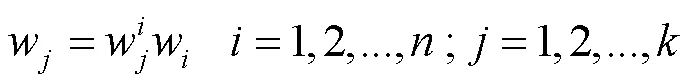
式中：w為優化指標層元素相對于目標層的權重。

通過以上計算，可得最終權重向量為：

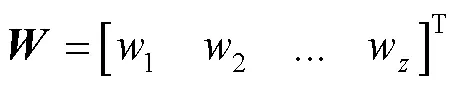
通過以上過程，利用GRA計算各個候選包裝材料的關聯系數，通過FAHP計算各個影響因素相對于目標層的權重，兩者相結合，最后比較關聯系數的大小，獲得最優包裝材料。

3 應用實例分析

將FAHP和GRA相結合的包裝材料優選方法應用在實際案例中，以證明方法的有效性。我司有一批待運輸的高壓電器設備，其中某型號隔離開關質量約為1 t，有4種包裝材料，通過實驗及查閱相關手冊，得到各個影響因素的值，通過式（10）—（13）計算得到無量綱評價值，結果見表3。

利用無量綱評價值矩陣作為評價矩陣，最優指標集為：

=

邀請設計、工藝、制造、一線包裝人員及運輸人員等7位專家，通過專家的評判，參照表2定義的模糊標度值，對優化指標層進行重要度排序，見表4。

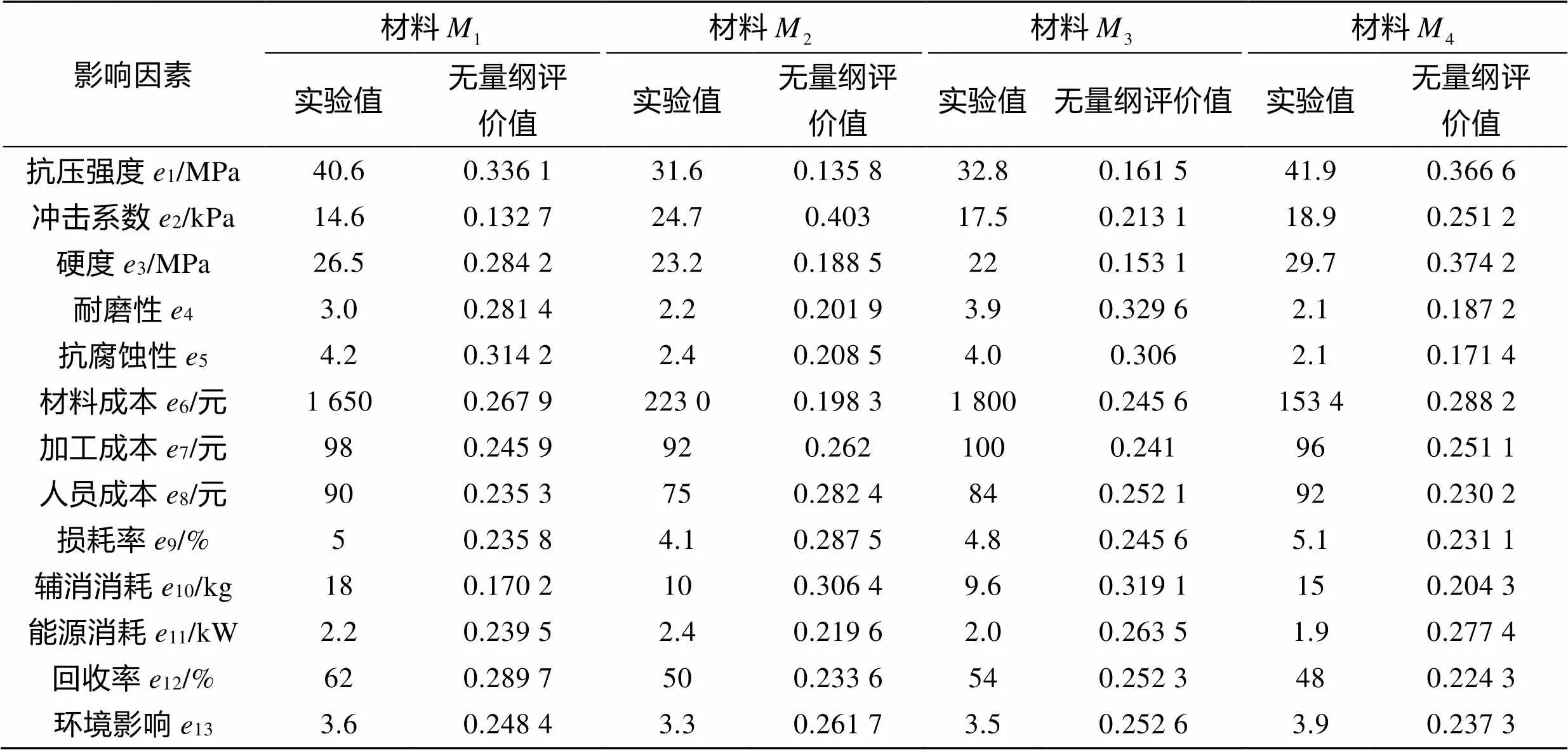
表3 候選包裝材料各影響因素的實驗值及其隸屬度

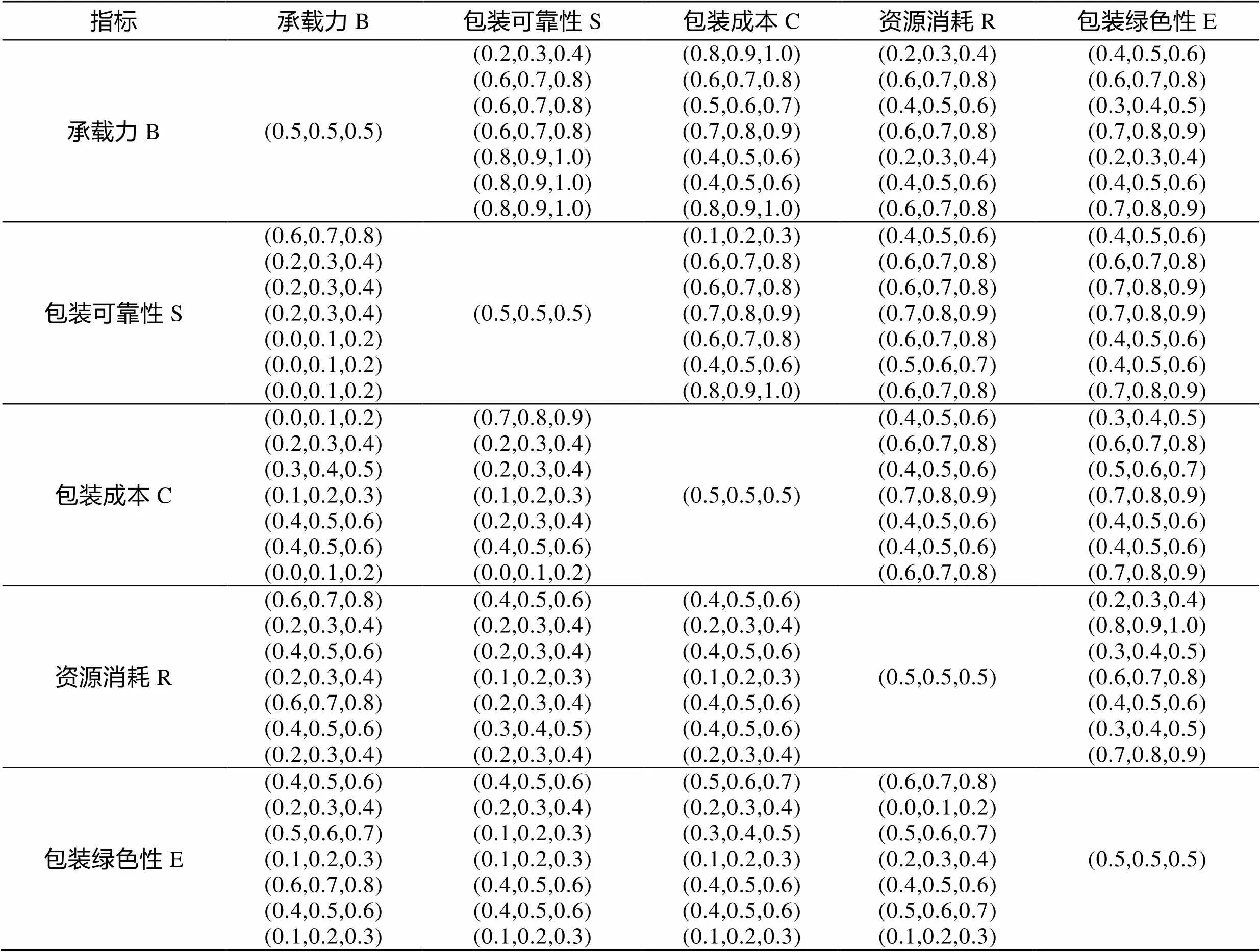
表4 優化指標層專家評價三角模糊矩陣

其中7位專家的權重分別為{0.17,0.09,0.12,0.1, 0.13,0.28,0.11}，通過加權平均獲得模糊判斷矩陣：

根據式（14）、式（15）求得可能度判斷矩陣：

根據式（16），計算出優化指標B、S、C、R、E相對于目標層的權重0為：

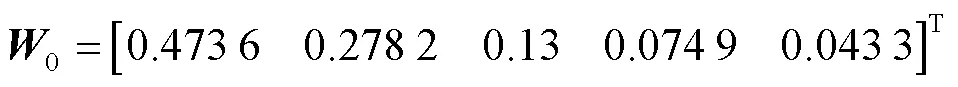
用同樣的方法計算各影響因素的權重：1、2、3相對于B的權重分別為0.664 6、0.286 8、0.048 6；4、5相對于S的權重分別為0.748、0.252；6、7、8相對于C的權重分別為0.601 4、0.297 9、0.100 7；9、10、11相對于R的權重分別為0.406 8、0.258、0.335 2；12、13相對于E的權重分別為0.748、0.252。

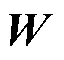
=[0.314 8 0.135 8 0.023 0.208 1 0.070 1 0.078 2 0.038 7 0.013 1 0.030 5 0.019 3 0.025 1 0.032 4 0.010 9]T

由式（5）、式（6）可以求得各候選包裝材料的綜合關聯程度為：

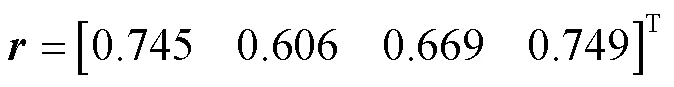
根據關聯系數從大到小進行排序為材料4、材料1、材料3、材料2，選取關聯程度最大的包裝材料為最終優選包裝材料，即包裝材料4。

4 結語

高壓電器設備包裝材料的合理是保證產品運輸可靠的重要前提，文中綜合分析了包裝材料選擇時各類影響因素，建立了影響包裝材料選擇的層次分析模型，包括5個優化目標和13個影響因素。建立了一種灰關聯分析法和模糊層次分析法相結合的包裝材料優選方法，根據不同的影響因素特征，采用組合隸屬度計算方法，克服了單一隸屬度計算下的片面性；在傳統三角模糊互補判斷矩陣評價方法的基礎上，進一步優化算法，提出了基于可能度的權重計算方法，使專家的判斷更加合理，并且降低主觀因素的影響。通過實例驗證，可有效進行包裝材料的選擇，證明了該方法的有效性。

[1] 袁彪, 汪永超, 劉曉晨, 等. 基于模糊層次分析法的刀具材料選擇[J]. 組合機床與自動化加工技術, 2016(10): 130-133.

YUAN Biao, WANG Yong-chao, LIU Xiao-chen, et al. Tool Material Selection Based on FAHP[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2016(10): 130-133.

[2] NEHA, AGGARWAL A G, JAISWAL A, Multi-objective Release Time Problem for Modular Software Using Fuzzy Analytical Hierarchy Process[J]. Springer Series in Reliability Engineering, 2022, 1: 159-191.

[3] 王偉賢, 孫舟, 潘鳴宇, 等. 基于模糊層次分析法的電動汽車充電樁信息安全風險評估方法[J]. 中國電力, 2021, 54(1): 96-103.

WANG Wei-xian, SUN Zhou, PAN Ming-yu, et al. Information Security Risk Assessment Method for Electric Vehicle Charging Piles Based on Fuzzy Analytic Hierarchy Process[J]. Electric Power, 2021, 54(1): 96-103.

[4] 陳偉華, 吳堅, 裘愉濤, 等. 組合模糊綜合評價法及其在輸電網規劃中的應用[J]. 浙江電力, 2020, 39(5): 100-106.

CHEN Wei-hua, WU Jian, QIU Yu-tao, et al. Combined Fuzzy Comprehensive Evaluation Method and Its Application in Transmission Network Planning[J]. Zhejiang Electric Power, 2020, 39(5): 100-106.

[5] LI J, ZHANG H, WANG Z, et al, A Fuzzy Evaluation Method of Power Transformer Insulation Health State Based on Multi-weight Fusion[J]. Journal of Electrical Engineering & Technology, 2022, 1: 1-12.

[6] 趙汝英, 張小飛, 鄭珞琳. 基于TOPSIS的電力通信網關鍵節點識別方法研究[J]. 電工技術, 2020(22): 92-94.

ZHAO Ru-ying, ZHANG Xiao-fei, ZHENG Luo-lin. Research on Identification Method of Key Nodes in Power Communication Network Based on TOPSIS[J]. Electric Engineering, 2020(22): 92-94.

[7] 榮飛, 毛燦, 周保榮, 等. 基于改進TOPSIS方法的柔性直流輸電系統電壓等級優選[J]. 高壓電器, 2021, 57(5): 21-28.

RONG Fei, MAO Can, ZHOU Bao-rong, et al. Voltage Level Optimization of Flexible HVDC System Based on Improved TOPSIS Method[J]. High Voltage Apparatus, 2021, 57(5): 21-28.

[8] BAFAIL O A, ABDULAAL R M. New Approach for Selecting a Suitable Recycling Collection Program for Recovered Paper and Pulp Recyclables Using AHP-TOPSIS Techniques[J]. Waste Management & Research: the Journal of the International Solid Wastes and Public Cleansing Association, ISWA, 2021, 39(11): 1406-1413.

[9] 李香飛. 基于不同隸屬度函數的金屬材料切削加工性模糊綜合評價[J]. 工具技術, 2019, 53(4): 67-72.

LI Xiang-fei. Fuzzy Comprehensive Evaluation of Machinability for Metal Materials Based on Different Membership Functions[J]. Tool Engineering, 2019, 53(4): 67-72.

[10] 劉蓉暉, 王毅超. 基于改進雷達圖法與高斯隸屬度相結合的電能質量綜合等級評估[J]. 電測與儀表, 2018, 55(14): 69-74.

LIU Rong-hui, WANG Yi-chao. Comprehensive Grade Evaluation of Power Quality Based on Improved Radar Chart Method and Gaussian Membership Degree[J]. Electrical Measurement & Instrumentation, 2018, 55(14): 69-74.

[11] 錢科軍, 秦萌, 宋遠軍, 等. 基于模糊隸屬度的充電站多目標優化調度[J]. 電力建設, 2020, 41(2): 118-124.

QIAN Ke-jun, QIN Meng, SONG Yuan-jun, et al. Multi-Objective Optimal Scheduling Based on Fuzzy Membership for Electric Bus Charging Station[J]. Electric Power Construction, 2020, 41(2): 118-124.

[12] KOSTEREY M, LITVINOV V. Development of Fuzzy Statistical Method of Optimal Resource Allocation Among Technical Departments of An Electric Utility Company[J]. Eastern-European Journal of Enterprise Technologies, 2016, 3(81): 20-27.

[13] 覃柏英. FAHP的標度系統與排序方法研究[D]. 南寧: 廣西大學, 2005: 13-16.

QIN Bo-ying. The Research of Scale System and Ranking Method of FAHP[D]. Nanning: Guangxi University, 2005: 13-16.

[14] DONG Qing-yun, WANG Tie-gang. Research on The Green Manufacturing Tool Scheme Evaluation Model Based on The Combination of Entropy Weight And a TOPSIS Method[J]. Machine Tool & Hydraulics, 2018, 46(12): 94-99.

[15] 李強, 汪永超, 李波, 等. 基于組合賦權法的GC–TOPSIS的機床夾具優選研究[J]. 制造技術與機床, 2020(5): 126-132.

LI Qiang, WANG Yong-chao, LI Bo, et al. Research on Optimal Selection of Machine Tool Fixture Based on Combination Weighting Method for GC-TOPSIS[J]. Manufacturing Technology & Machine Tool, 2020(5): 126-132.

[16] RAJYALAKSHMI M, RAO M V. Multi-Response Optimization of Machining Factors in Pocket Milling of AISI304 Using Grey Relational Analysis[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1112(1): 1-9.

[17] 劉長銀, 宋人杰, 趙萌, 等. 基于變權重和組合隸屬度函數的GIS氣體絕緣狀態評估[J]. 高壓電器, 2021, 57(6): 102-106.

LIU Chang-yin, SONG Ren-jie, ZHAO Meng, et al. Gas Insulation State Assessment of GIS Equipment Based on Variable Weight and Combined Membership Function[J]. High Voltage Apparatus, 2021, 57(6): 102-106.

[18] WANG Y, CHIN K. Fuzzy Analytic Hierarchy Process[J]. International Journal of Approximate Reasoning, 2011, 52(4): 541-553.

[19] LIU W, CHANG J, MENG J, et al. Ranking Method of Additive Consistent Fuzzy Judgment Matrix Considering Scale[J]. System Engineering Theory and Practice, 2018, 38(7): 1836-1841.

[20] 趙璇, 張強, 朱吉喬. 模糊數互補判斷矩陣的乘性一致性檢驗及改進方法[J]. 運籌與管理, 2013, 22(3): 1-8.

ZHAO Xuan, ZHANG Qiang, ZHU Ji-qiao. Multiplicative Consistency Test and Modification Approach of Fuzzy Number Complementary Judgment Matrix[J]. Operations Research and Management Science, 2013, 22(3): 1-8.

[21] 朱吉喬, 張強, 趙璇. 模糊數互補判斷矩陣的乘性一致性研究[J]. 運籌與管理, 2013, 22(1): 29-35.

ZHU Ji-qiao, ZHANG Qiang, ZHAO Xuan. On the Multiplicative Consistency of Fuzzy Number Complement Judgment Matrix[J]. Operations Research and Management Science, 2013, 22(1): 29-35.

[22] 呂躍進, 蔣建軍, 劉洪梅. 基于乘性模糊互補判斷矩陣的FAHP[J]. 模糊系統與數學, 2012, 26(2): 98-104.

LYU Yue-jin, JIANG Jian-jun, LIU Hong-mei. FAHP Based on Multiplicative Consistency Fuzzy Complementary Judgment Matrix[J]. Fuzzy Systems and Mathematics, 2012, 26(2): 98-104.

[23] 甘庭聰, 徐義紅, 張雨涵. 三角模糊數的一種排序方法[J]. 數學的實踐與認識, 2020, 50(13): 116-121.

GAN Ting-cong, XU Yi-hong, ZHANG Yu-han. A Ranking Method of Fuzzy Triangular Fuzzy Numbers[J]. Mathematics in Practice and Theory, 2020, 50(13): 116-121.

[24] 甘庭聰. 三角模糊數的排序公式及應用[D]. 南昌: 南昌大學, 2017: 14-17.

GAN Ting-cong. The Ranking Formula of Triangular Fuzzy Number and Its Applications[D]. Nanchang: Nanchang University, 2017: 14-17.

[25] 徐澤水. 三角模糊數互補判斷矩陣的一種排序方法[J]. 模糊系統與數學, 2002, 16(1): 47-50.

XU Ze-shui. A Method for Priorities of Triangular Fuzzy Number Complementary Judgment Matrices[J]. Fuzzy Systems and Mathematics, 2002, 16(1): 47-50.

Selection of Packaging Materials for High-voltage Electrical Equipment

GAO Ling, WANG Pu, YI Peng

(Xi'an XD Switchgear Electric Co., Ltd., Xi'an 710077, China)

The work aims to realize the selection of packaging materials for high-voltage electrical equipment, improve the consistency and economy of packaging materials selection, and reduce manufacturing costs. A multi-objective material selection model including five optimization objectives such as packaging bearing capacity, packaging reliability, packaging cost, resource consumption and packaging greenness was established. The evaluation index set was constructed with the combined membership function, and the material selection was realized by combining the grey crelational analysis (GRA) method with the fuzzy analytic hierarchy process (FAHP) based on the possibility ranking algorithm. The correlation coefficients of candidate materials were 0.745, 0.606, 0.669 and 0.749. The packaging material with the largest correlation coefficient is the final preferred packaging material.

high-voltage electrical equipment; packaging material selection; grey relational analysis (GRA); triangular fuzzy number; fuzzy analytic hierarchy process (FAHP)

TB484；TM564

A

1001-3563(2023)01-0279-07

10.19554/j.cnki.1001-3563.2023.01.032

2022?06?10

高嶺（1993—），男，碩士，工程師，主要研究方向為制造業信息化。

責任編輯：曾鈺嬋