改進的VIP法在大壩監測效應量關鍵影響因子識別中的應用

李詩婉，劉可心，周子玉，李艷玲

(1.四川大學水利水電學院 水力學與山區河流開發保護國家重點實驗室，四川 成都 610065；2.江陰市璜土鎮人民政府，江蘇 江陰 214445)

1 概述

環境量對于大壩安全監測具有十分重要的作用，如庫水位對土石壩滲流的影響[1]，溫度對混凝土壩變形的影響[2]等。通過應用各種數學、力學等方法[3]，結合環境量建立大壩安全監測模型[4]，分析環境分量對監測效應量的影響程度，可以更好地針對這些影響大壩效應量的關鍵因素實施監控，并且能夠定量分析它們對于監測效應量的影響，更好地把握大壩的運行性態。

1956年，意大利的Tonini[5]最早將影響大壩位移的主要因素劃分為水壓、溫度和時效3個分量，隨后各國學者紛紛推動跟進。在國內，顧沖時[6]首次采用最小二乘法獲得了大壩水壓變化分量和溫度變化分量以及時效效應分量；王建[7]和陳宇清[8]分別提出了結合距離概念的加權面積法和應用灰色系統理論的灰色關聯分析法來描述環境量對效應量的影響效應，并且都取得了不錯的應用效果。但是，加權面積法識別結果很大程度上依賴于建模因子的選取，灰色關聯分析法對于數據異常突跳具有很強的敏感性，從而容易造成大壩監測效應量關鍵影響因子的誤判。因此，本文提出了改進的變量投影重要性分析法，該方法基于偏最小二乘回歸，提供可以對數據進行深入分析的輔助分析技術，結合水利工程的特性對變量投影重要性指標進行改進，是一種較好的變量選擇方法，適用于樣本較少、相關性較強的數據[9]，并通過工程實例的應用，驗證本文方法的可靠性和準確性。

2 基于偏最小二乘的VIP改進方法

在偏最小二乘法計算過程中[10]，所提取的因子主成分th對分量X、xj或y的解釋能力就相當于X、xj或y關于th的線性回歸方程的復測定系數R2。其值越大，就說明解釋能力越強。定義th的各種解釋能力如下：

th對某個因子xj的解釋能力：

Rd(xj,th)=r2(xj,th)

(1)

th對X的解釋能力：

(2)

th對y的解釋能力：

Rd(y,th)=r2(y,th)

(3)

基于th的解釋能力，即可得到變量投影重要性指標VIPj：

(4)

式中，k—自變量個數；Rd(y,t1，t2，…，tm)—因變量和主成分的相關系數，表示t1，t2，…,tm對y的累計解釋能力；whj—軸wh的第j個分量，表示該自變量在主成分上的權重，在這里，它被用于測量xj對構造th成分的邊際貢獻，對于任意h=1，2，…，m，則有：

(5)

根據變量投影重要性分析法的基本原理可以發現，VIPj表示自變量對因變量的解釋能力，該指標能夠說明哪些自變量相對而言對于因變量的作用更大一些。在水利工程中，自變量xj為環境量因子，通過力學理論及類似工程經驗，構建合理的大壩安全監測統計回歸模型，確定對效應量有影響作用的環境量因子。由于所有環境量因子xj對于監測效應量y的總影響應為1，因此，根據式(5)可以將式(4)改進為：

(6)

圖1 改進的VIP法識別關鍵影響因子流程圖

3 應用效果分析

3.1 多重共線性影響分析

以某土石壩左岸山體繞壩滲流測點AUP1的實測數據為例，構建繞壩滲流統計回歸模型見式(7)，其統計分析成果見表1。從表1中可以看出，統計回歸效果較理想，復相關系數為0.954，但14個模型因子中6個方差膨脹因子(VIF)大于10，最大值達5255.70，這說明模型因子間存在著嚴重的多重共線性。

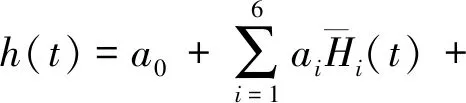
(7)

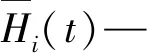
為進一步說明多重共線性對關鍵影響因子識別的影響，使用測點AUP1的實測數據(共313個測次)進行不同方式的抽樣得到5個不同數據量的數據樣本，并根據5個樣本分別建立統計回歸模型，獲取各因子的回歸系數，見表2、如圖2所示。從圖表中可以看出，對于5個不同的樣本，其復相關系數都相當理想，也都通過了F檢驗，但部分因子回歸系數的波動較大。

分別采用加權面積法和改進的變量投影重要性分析法對AUP1測點實測數據樣本1—5進行關鍵影響因子識別，得到該測點的影響因子識別結果見表3。通過表3可以看出，對于5個不同的樣本，采用加權面積法進行效應量關鍵影響因子識別結果受數據變化影響較大，穩定性和可靠性低。

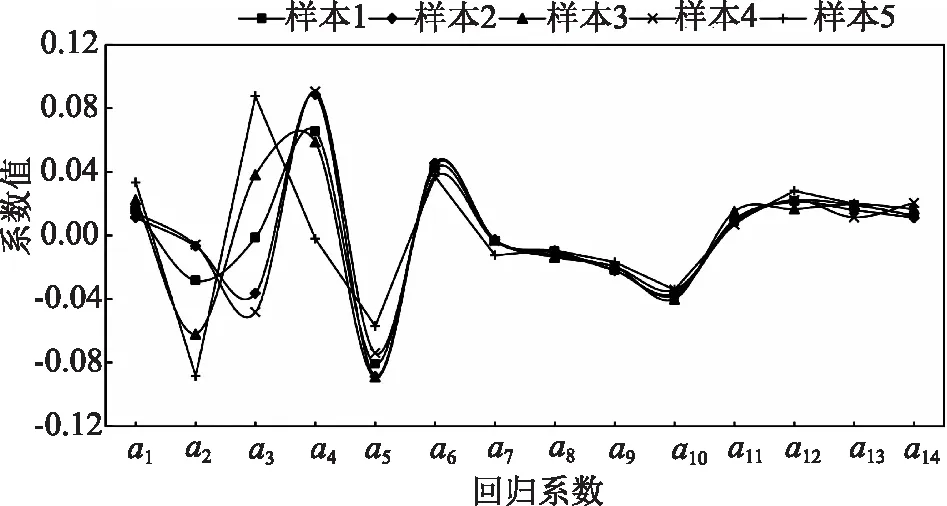
圖2 測點AUP1在不同抽樣下的最小二乘回歸系數

加權面積法的核心是結合距離的概念，根據統計回歸模型中的各環境因子回歸系數構建分量-時間曲線，將分量至某一基準值的平均距離作為衡量標準，因此，該方法識別關鍵影響因子的精度在很大程度上取決于模型因子回歸系數的穩定性。而由于多重共線性的存在，回歸系數對效應量監測序列中數據的微小變化可能會非常敏感，回歸系數的穩定性會變差，從而導致加權面積法確定的效應量分量比例可靠性降低。而采用改進的變量投影重要性分析法采用循環式的信息分解與提取方法，從環境量集中提取成分，然后對所提取的成分進行普通的多元回歸，由于所提取的成分都線性無關，從而能夠有效消減變量間多重共線性影響，因此識別出的關鍵影響因子和次關鍵影響因子均為降雨和水位，且各環境量的影響占比相差不超過3%，能夠克服效應量監測序列中數據的微小變化，其對相同測點不同數據量的數據序列識別結果穩定性明顯優于加權面積法。

3.2 抗噪能力分析

以某閘壩壩頂外觀垂直位移測點CTP4為例，由于該閘壩垂直位移觀測墩的監測方式為人工監測，頻率為1次/月，溫度的監測方式為自動化監測，頻率為1次/d，其原觀監測數據與測點觀測當日溫度的歷時過程線、溫度原觀監測數據歷時過程線如圖3所示，使用單測點統計回歸模型。

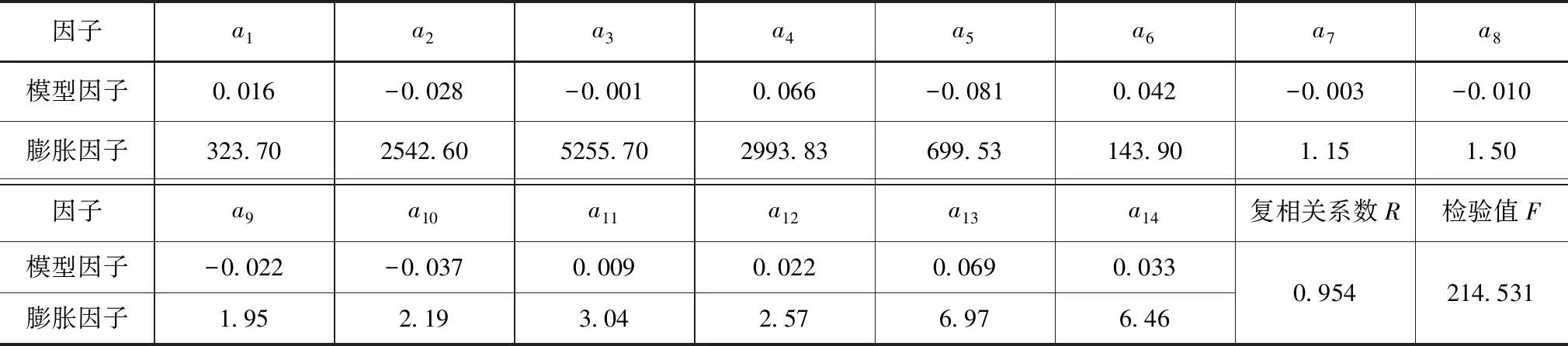
表1 繞滲測點AUP1回歸結果統計

表2 測點AUP1原觀監測的5個抽樣樣本及回歸結果

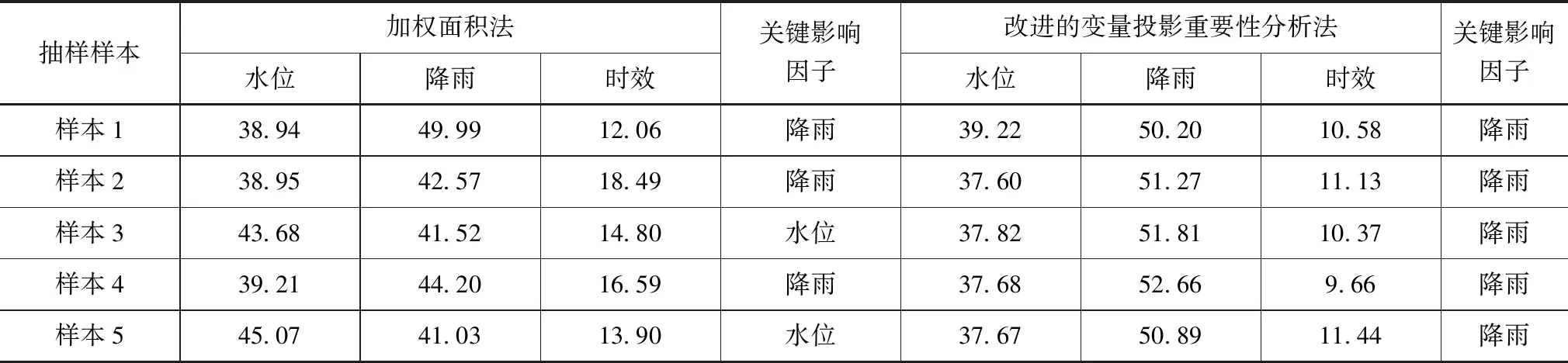
表3 測點AUP1不同抽樣下的關鍵影響因子識別結果 單位：%

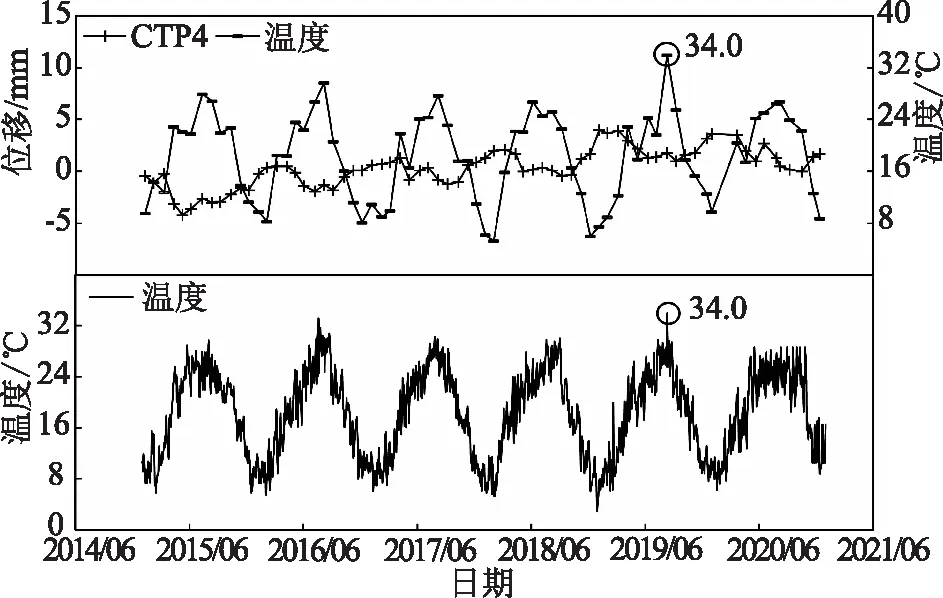
圖3 測點CTP4及溫度歷時過程線

單測點統計回歸模型如下：

(8)

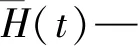
從圖4可以發現，CTP4測點2019年8月測次對應的溫度值出現突跳，達到34.0℃，但該測次前1天的溫度測值僅25.5℃，溫度序列出現了單次突跳。為分析溫度測值突變、不同溫度測值提取模式等對關鍵因子識別效果的影響，設置了3個方案進行對比分析。

將該測點原觀監測數據作為目標數據列：

X0={X0(t),t=1,2,…,n}；

(1)觀測當日環境量作為比較數據列1：

X1i={X1i,t=1,2,…,n;i=2}；

(2)將比較數據列1中2019年8月測次的溫度數據修正為該測次前一天的溫度實測值25.5℃作為比較數據列2：

X2i={X2i,t=1,2,…,n;i=2}；

(3)由于該測點垂直位移效應量的監測頻率為1次/月，因此再將比較數據列1中的溫度數據取各月均值作為比較數據列3：

X3i={X3i,t=1,2,…,n;i=2}；(其中，i=1時為水位分量；i=2時為溫度分量；i=3時為時效分量)。

采用灰色關聯分析法針對目標數據列和比較數據列1、2、3進行關鍵影響因子識別，采用改進的變量投影重要性分析法針對目標數據列和比較數據列1、2進行關鍵影響因子識別，得到該測點的影響因子識別結果見表4。可以發現灰色關聯分析法應用灰色系統理論，將水位、溫度、時效等環境量和效應量觀測數據作無量綱處理，并將效應量作為參考數列，環境量因子作為比較數列，分別求解其關聯系數和關聯度，并將歸一化后的關聯度作為環境量對大壩效應量的影響程度。但是3次識別的關鍵影響因子結果并不一致，溫度影響占比相差最大達到了17.58%，這說明灰色關聯分析法的抗噪能力較差，監測序列的單次突跳對識別結果影響很大，同時當環境量和效應量監測頻次不一致時難以選擇合理的目標數據列和比較數據列，不同的選取方式會造成識別結果產生很大的差異，甚至會造成關鍵影響因子的誤判。當采用改進的變量投影重要性分析法進行關鍵影響因子識別時，該方法通過提取變量中解釋能力最強的綜合變量，相較于灰色關聯分析法對各測點的關鍵影響因子識別不會因效應量與環境量數據列的異常突跳而產生差異，同時也能夠避免效應量與環境量監測頻次不一致而難以選擇數據列的問題，計算出來的環境分量占比更穩定，相差不超過2%。

綜上所述，加權面積法易受統計回歸模型的精度和合理性影響，且受數據量的微小變化影響很大；灰色關聯分析法受制于本身極大程度依靠數學處理的特性，無法從力學角度進行合理解釋，同時效應量或環境量監測序列的單次突跳、效應量與環境量的觀測頻次不一致均可能對識別結果產生很大影響。然而基于偏最小二乘回歸的變量投影重要性改進分析法，采用循環式的信息分解與提取方法，從環境量集中提取變量中解釋能力最強的綜合變量，從而有效克服上述問題，具有較強的適用性。

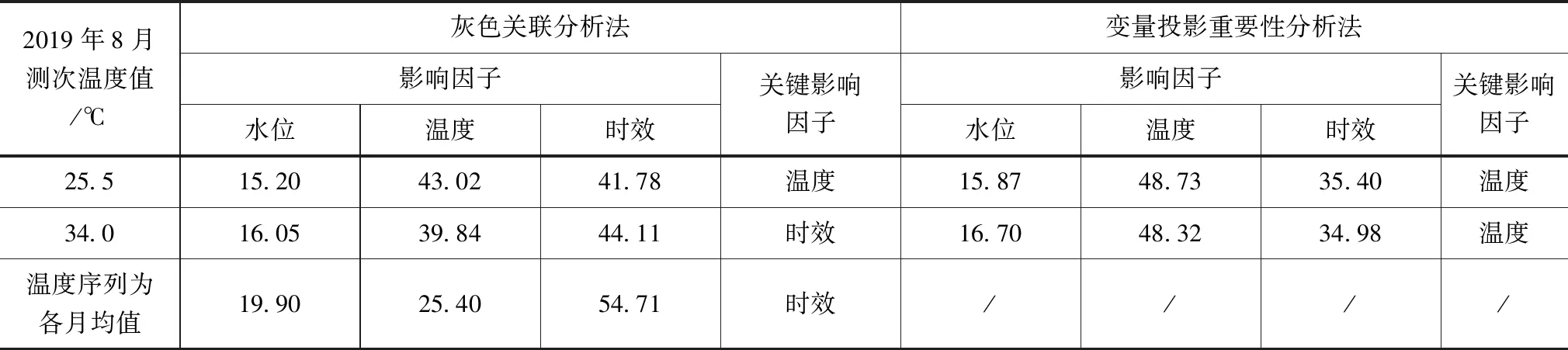
表4 不同方法對測點CTP4的關鍵影響因子識別結果 單位：%

4 結論

針對加權面積法和灰色關聯分析法在大壩安全監測效應量關鍵影響因子識別時的主要問題，提出了改進的變量投影重要性分析法，并從穩定性和適用性等方面分析其應用效果，得到了如下結論：

(1)加權面積法基于統計回歸模型，監測序列中數據的微小變化可能造成回歸系數估計值的很大波動，而改進的變量投影重要性分析法具備良好的穩定性，能有效降低因子間多重共線性。

(2)相較于依靠數學統計的灰色關聯分析法處理波動型數據時識別結果可靠性差的問題，改進的變量投影重要性分析法能有效降低數據序列異常突跳的不利影響，并且克服環境量和效應量監測頻次不一致時數據列的不同選擇導致對大壩監測效應量的關鍵影響因子產生誤判現象。

(3)本文基于偏最小二乘回歸，提出的改進變量投影重要性分析法具備良好的可靠性性和適用性，較加權面積法和灰色關聯分析法具有明顯的優勢。