基于SNN-LSTM的小樣本數據下軸承故障診斷方法*

呂云開,武 兵,2*,李聰明,2

(1.太原理工大學 機械與運載工程學院,山西 太原 030024;2.太原理工大學 新型傳感器與智能控制教育部重點實驗室,山西 太原 030024)

0 引 言

當前,故障診斷技術廣泛應用于汽車、航空航天、電氣、制造業等多個領域。

在使用滾動軸承的機械裝備中,大約有30%的機械故障是由滾動軸承的損壞引起的,可見滾動軸承的工作狀態在很大程度上影響著整個機械設備的運行狀態。因此,軸承故障診斷技術的研究一直是機械故障診斷中的重中之重。

目前,故障診斷技術主要是基于信號處理的方法以及基于人工智能的方法[1]。其中,基于信號處理的方法是利用信號分析技術來分析時域、頻域以及時頻域的特征。

夏理健等人[2]對滾動軸承振動信號進行完備總體經驗模態分解后,選擇固有模態函數分量,求出了其散布熵和Hjorth參數,最后將其輸入到支持向量機中,實現了對軸承故障的分類診斷。彭程程[3]通過構建軸承振動信號的二階頻率變化模型,以及觀察短時傅里葉變換時頻圖,進行了軸承的故障診斷。LI W等人[4]利用數學形態學中的開運算、閉運算,對信號進行了濾波、去噪,利用香農熵的定義獲得了歸一化形態譜熵,采用改進的準解析復小波變換分解,實現了對軸承的故障診斷。NI Q等人[5]采用廣義高斯循環分析模型和廣義高斯分析模型,并結合特定的統計閾值,近似確定了模態數,然后定義了故障特征幅值比,確定了最優帶寬控制參數,并將信號進行了變分模態分解,最后進行了軸承的故障診斷。

近年來,基于深度學習的軸承故障診斷方法備受人們的關注,因為該方法可以克服人工分析方法相對耗時、主觀的缺點,具有能夠自適應地從振動信號中提取故障特征的能力。FANG Q等人[6]采用3層卷積神經網絡與門控循環單元相結合來提取特征,并且引入自注意力機制,并輸入到自歸一化網絡,對軸承進行了故障診斷。賈峰等人[7]采用深度卷積神經網絡,提取了軸承的樣本特征,然后采用加權領域鑒別器,解決了“目標域中出現額外故障樣本會影響軸承故障診斷精度”的問題。LING Hai-tao等人[8]首先通過連續小波變換生成了時頻圖,之后采用卷積神經網絡以及雙向長短時記憶網絡,提取了故障特征,最后將其輸入到數字膠囊網絡中,從而完成了對軸承故障的分類診斷。

為了實現以上深度學習的方法,需要用到大量的、有標注的訓練樣本,而在小樣本數據下,采用這些方法會產生模型欠擬合問題,同時采用該方法獲得的分類準確率也較低。

為了解決以上問題,筆者提出一種結合孿生神經網絡與長短時記憶網絡的軸承故障診斷方法,即以一對帶有正負標簽的原始振動信號樣本作為診斷方法的輸入,使用參數共享的卷積層、池化層以及長短時記憶網絡層,提取輸入樣本對的特征,通過計算二者之間的曼哈頓距離,判斷輸入樣本對的相似度,最后在小樣本數據下,實現對不同狀態軸承的分類診斷。

1 SNN-LSTM故障診斷模型

1.1 卷積神經網絡

卷積神經網絡(convolutional neural networks,CNN)[9]具有強大的特征提取能力,是深度學習中的代表網絡。

一般情況下,卷積神經網絡主要由卷積層、池化層、全連接層等組成。卷積層是采用一定數量大小的卷積核,對上一層輸出的樣本進行卷積運算,加上偏置向量,通過激活函數的激活,然后作為下一層的輸入。

卷積核數量的多少對應著下一層的深度,卷積的數學公式如下所示:

Xl=f(Wl*X(l-1)+bl)

(1)

式中:X(l-1)—第l-1層的輸入;Wl—第l層里卷積核的權重矩陣;bl—偏置向量;f()—第l層的激活函數;Xl—經過卷積計算后第l層的輸出,也是下一層的輸入。

經過卷積運算后,需要用到非線性激活函數進行非線性變換,來增強模型的擬合能力。常見的激活函數有ReLU、sigmoid、SoftMax等,其數學公式分別如下所示:

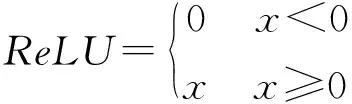
(2)

(3)

(4)

在上式中:ReLU激活函數由于其簡單的運算被用于卷積層、池化層等進行激活,可以加速模型的收斂速度。

sigmoid激活函數在輸入較大的情況下會出現軟飽和性,從而導致梯度無法向后傳遞、更新參數,進而導致梯度消失。因此,sigmoid激活函數一般不作為卷積層的激活函數,通常在二分類問題中作為輸出層的激活函數來輸出概率。

SoftMax激活函數則常用于多分類問題中,作為輸出層的激活函數來輸出概率。

經過卷積層后的特征維度一般比較大,使用池化層可以有效地降低特征維度,防止由于模型參數過多從而產生的過擬合問題。

池化層的運算如下所示:

O(l+1)=Fpool(Xl)

(5)

式中:Xl—第l層經過卷積層進行激活后的輸出;O(l+1)—經過池化層后的輸出。

常用的池化層有最大池化層以及平均池化層,筆者所采用的是最大池化層。

1.2 孿生神經網絡

孿生神經網絡是為了解決小樣本學習問題[10]而提出的一種網絡結構。

現階段,孿生神經網絡主要用于食品識別、語音識別、人臉識別、表情識別等領域[11]。而將孿生神經網絡用于軸承故障診斷的研究目前還比較少。

孿生神經網絡的結構如圖1所示。

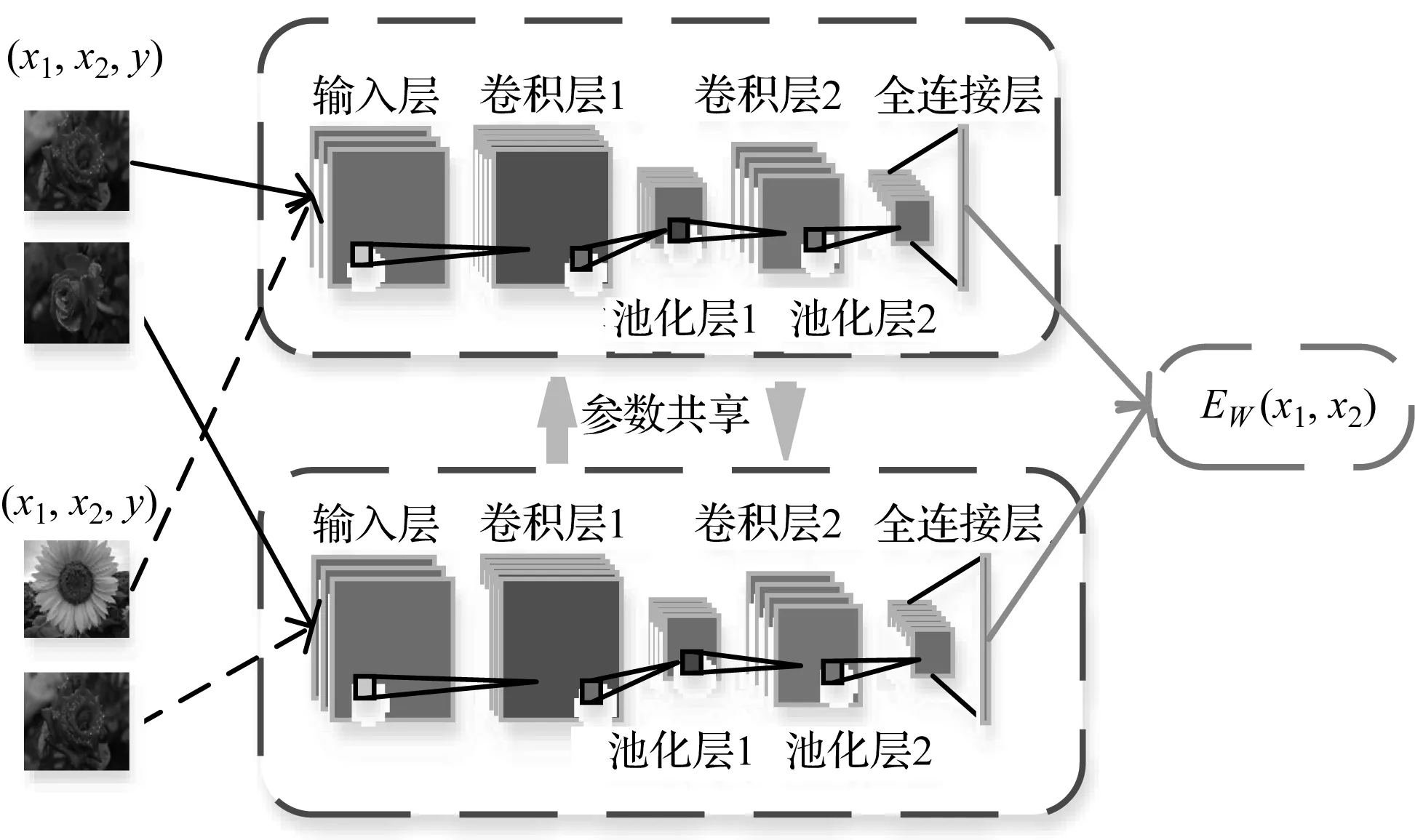
圖1 孿生神經網絡原理圖

這是一種可以學習2個樣本之間相似度的網絡。輸入的樣本是一個樣本對(x1,x2,y)。其中:y=1表示2個樣本是來自同一類;y=0表示2個樣本來自不同類。

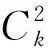
將一對樣本輸入到參數共享的兩個神經網絡中,通過網絡輸出得到fw(x1),fw(x2),之后將其輸入到能量函數E中,表達式如下所示:

Ew(x1,x2)=‖fw(x1)-fw(x2)‖

(6)

式中:Ew(x1,x2)—兩個輸入之間的相似度。

能量函數E可以是任意相似性度量函數,常見的有:曼哈頓距離、歐氏距離、閔可夫斯基距離、余弦相似度等。其中,歐式距離等既要涉及加減運算,還需要進行開方運算,從而容易導致計算相對麻煩。

而曼哈頓距離只涉及加減運算,并且可以消除開方過程中取近似值帶來的誤差。因此,此處筆者所用的是曼哈頓距離。

曼哈頓距離表達式如下所示:

df(x1,x2)=|fw(x1)-fw(x2)|

(7)

式中:輸出—fw(x1),fw(x2)兩個向量之間的曼哈頓距離。

孿生神經網絡的輸出是樣本對的相似性,也是樣本對來自相同類的概率,其公式如下所示:

P(x1,x2)=sigm(FC(df(x1,x2)))

(8)

式中:FC—全連接層;sigm—sigmoid激活函數。

孿生神經網絡中,常見的損失函數為二元交叉熵損失函數以及對比損失函數[12],二者單次訓練的損失函數公式分別如下所示:

Loss1(P(x1,x2),y)=-ylog(P(x1,x2))-(1-y)log(1-P(x1,x2))

(9)

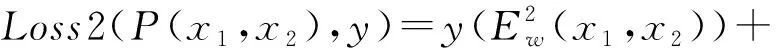
(10)

式中:P(x1,x2)—一對樣本的預測相似度;y—真實標簽0或1;Ew(x1,x2)—能量函數;margin—超參數閾值:當輸入的兩個樣本不相似、二者距離大于這個閾值時損失為零。

由于對比損失函數需要調整超參數,此處筆者選用二元交叉熵損失函數。

最后,通過相似度的分析[13],就可以判斷測試樣本應該屬于哪一類。

1.3 長短時記憶網絡

長短時記憶網絡[14]是為了改善在循環神經網絡中,長序列樣本在訓練過程中存在的梯度消失、梯度爆炸等問題,而提出的改進網絡。

長短時記憶網絡的核心思想是,可以通過遺忘不同程度的長時記憶,并加上此刻產生的短時記憶,從而來控制此時刻經過長短時記憶網絡所產生的輸出值。

長短時記憶網絡主要由遺忘門、輸入門和輸出門來控制其輸出值。

遺忘門用來記錄長時記憶的遺忘程度,決定上一時刻的記憶細胞狀態有多少保留到此刻的記憶細胞狀態。

遺忘門的公式如下所示:

ft=σ(Wf·[ht-1,xt]+bf)

(11)

式中:ht-1—上一時刻的輸出;xt—當前時刻的輸入;Wf—遺忘門的權重矩陣;bf—偏置向量;σ—sigmoid激活函數;ft—遺忘門的輸出。

輸入門用來記錄當前時刻的短時記憶,決定這一時刻有多少信息被保留。

輸入門公式如下所示:

it=σ(Wi·[ht-1,xt]+bi)

(12)

(13)

(14)

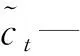
輸出門用來作為長短時記憶網絡最后的輸出,其公式如下所示。

ot=σ(Wo·[ht-1,xt]+bo)

(15)

ht=ot·tanh(ct)

(16)

式中:Wo—輸出門的權重矩陣;bo—輸出門的偏置向量;ht—最后的輸出,由輸出門的輸出和該時刻的記憶細胞狀態決定。

1.4 SNN-LSTM

最終,筆者所確定的網絡結構如圖2所示。

圖2 SNN-LSTM網絡原理圖

網絡的輸入是原始振動信號的一對樣本,標簽為0或1。筆者采用比較二者相似度的方法來擴充訓練樣本個數,使其更適用于小樣本數據。

筆者通過共享提取樣本對特征的網絡參數來完成孿生神經網絡的搭建,經過卷積層、池化層提取特征后,用長短時記憶網絡層進一步提取有關時間序列的特征,最后進行全連接,并計算二者曼哈頓距離,從而輸出0到1之間的值,利用真實標簽和二元交叉熵損失函數,進行梯度反向傳播,更新網絡參數。

SNN-LSTM網絡主要參數如表1所示。

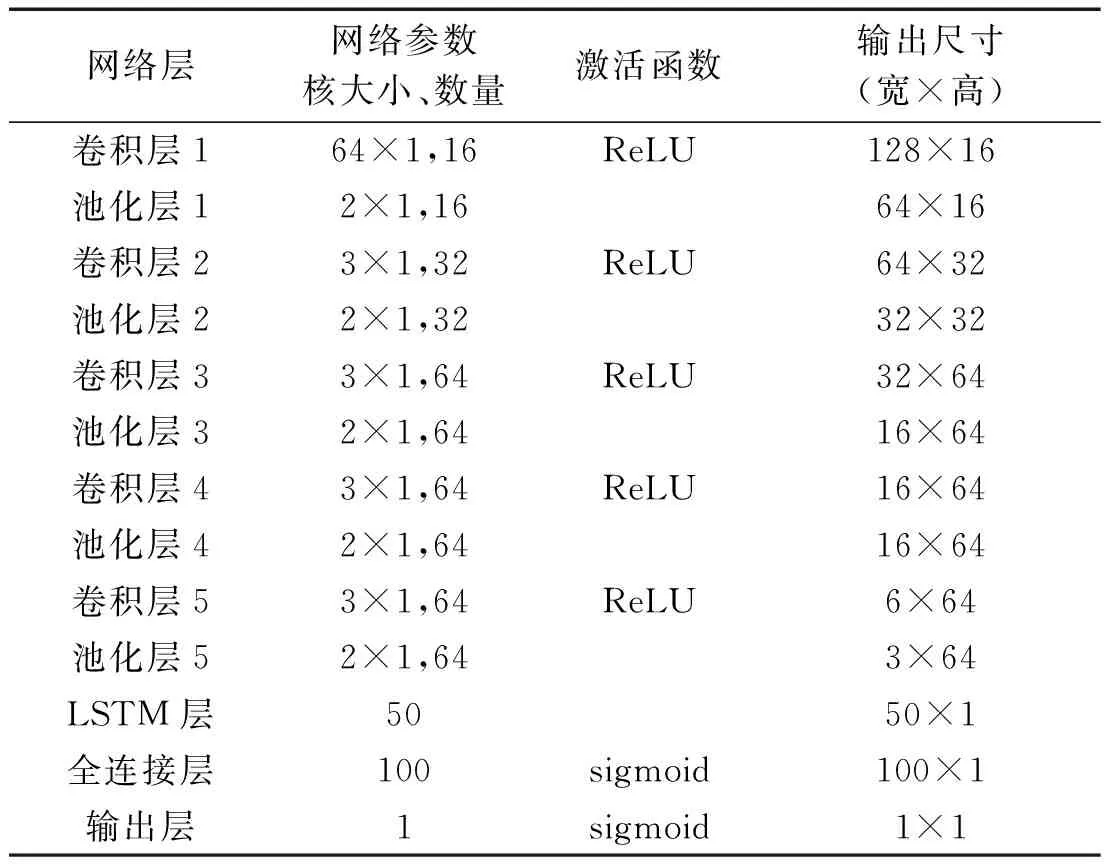
表1 SNN-LSTM網絡主要參數

SNN-LSTM采取小而深的網絡結構,第一層卷積核過小,容易受到高頻噪聲的干擾;而過大,則容易丟失局部特征。因此,筆者認為采用中等大小的卷積核比較合適[15]。

基于SNN-LSTM的故障診斷模型訓練以及測試步驟,如圖3所示。

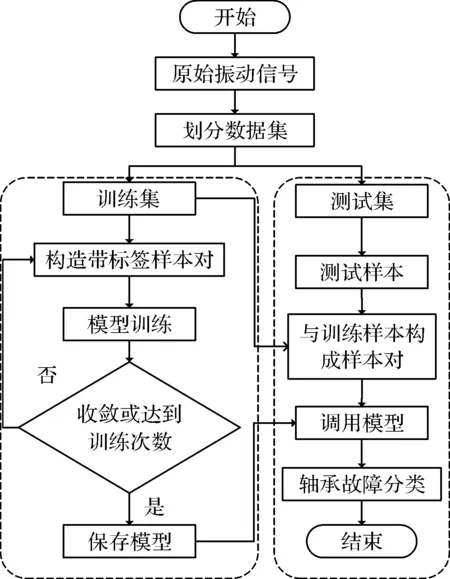
圖3 SNN-LSTM網絡故障診斷模型流程圖

基于SNN-LSTM的故障診斷具體步驟如下:

(1)劃分數據集。對采集到的原始振動信號進行劃分,劃分出訓練集與測試集;

(2)模型訓練。每次在訓練集中抽取兩個樣本,形成樣本對輸入到SNN-LSTM網絡中,通過損失函數進行梯度下降,反向傳播到網絡中,從而更新網絡參數。當模型訓練到一定次數或者收斂時,停止訓練,保存模型;

(3)測試樣本故障分類。在測試集中隨機選擇一個樣本作為測試樣本。

在訓練集中,每一類分別選擇一個樣本,將其與測試樣本一起,輸入到SNN-LSTM網絡中,得到測試樣本屬于每一類的概率值,選擇概率最大那個類作為測試樣本的類別。

2 實驗數據及信號采集

2.1 實驗數據

為了驗證基于SNN-LSTM的故障診斷方法在軸承故障診斷中的有效性,筆者設計了一個軸承故障診斷實驗,采集了不同轉速、不同狀態下的軸承振動數據[16]。

數據來源于Machinery Fault Simulator-Lite軸承故障診斷實驗臺。

實驗臺結構如圖4所示。

圖4 Machinery Fault Simulator-Lite軸承故障診斷實驗臺

筆者選用DEWE 43V采集卡采集傳感器上的加速度信號。

其中,傳感器品牌及型號為:KISTLER-8766A050。電動機轉速分別為:1 200 r/min、1 800 r/min、2 400 r/min。軸承型號為:ER12K-HFF深溝球軸承。

采樣頻率為12 kHz,正常軸承采樣時間為4 min,其他有故障的軸承采樣時間為2 min。

傳感器采集軸承基座上的振動信號,所采集到的故障類型是單一故障。其在1 200 r/min轉速下,采集正常、滾動體故障、內圈故障和外圈故障4種狀態的軸承振動信號;在1 800 r/min轉速下,采集滾動體故障、內圈故障和外圈故障3種狀態的軸承振動信號。

故障尺寸大小為1.5×0.8 mm,為電火花點蝕加工。

每種狀態下所截取的信號長度為120 000個點,一半數據生成訓練集,另一半生成測試集。每2 048個點為一個樣本,在訓練集上采用大小為2 048個點、滑動步長為80個點的滑動窗口生成訓練樣本,通過重疊采樣的辦法,可以擴充訓練樣本數量。

測試集上用同樣大小的窗口生成測試樣本,不采取重疊滑動。一共有7種不同狀態類別,每個類別包括300個訓練樣本和100個測試樣本。

數據集描述如表2所示。

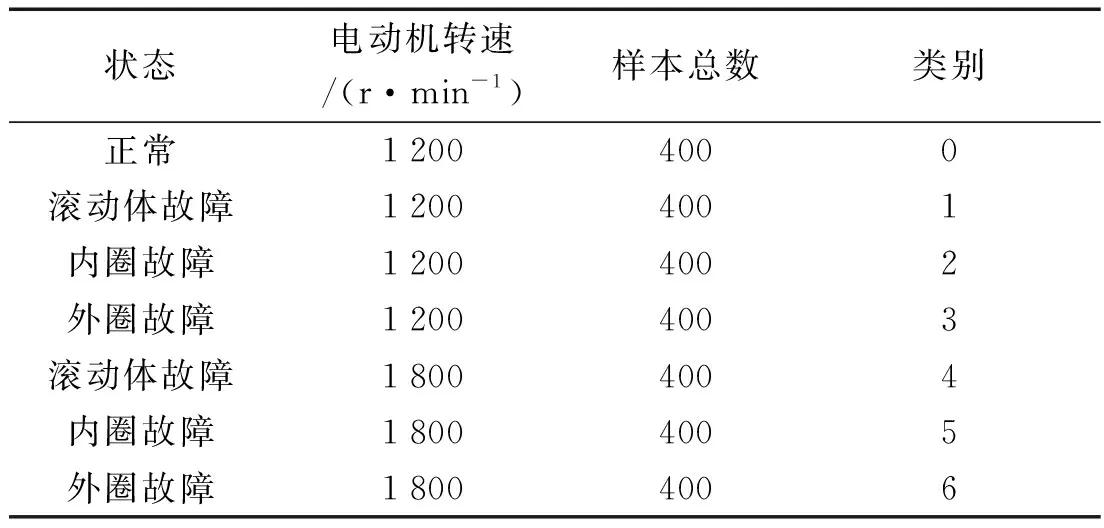
表2 數據集描述

2.2 振動信號波形圖

實驗中,筆者采集到了在1 200 r/min轉速下的4種狀態的軸承振動信號時域波形圖,如圖5所示。

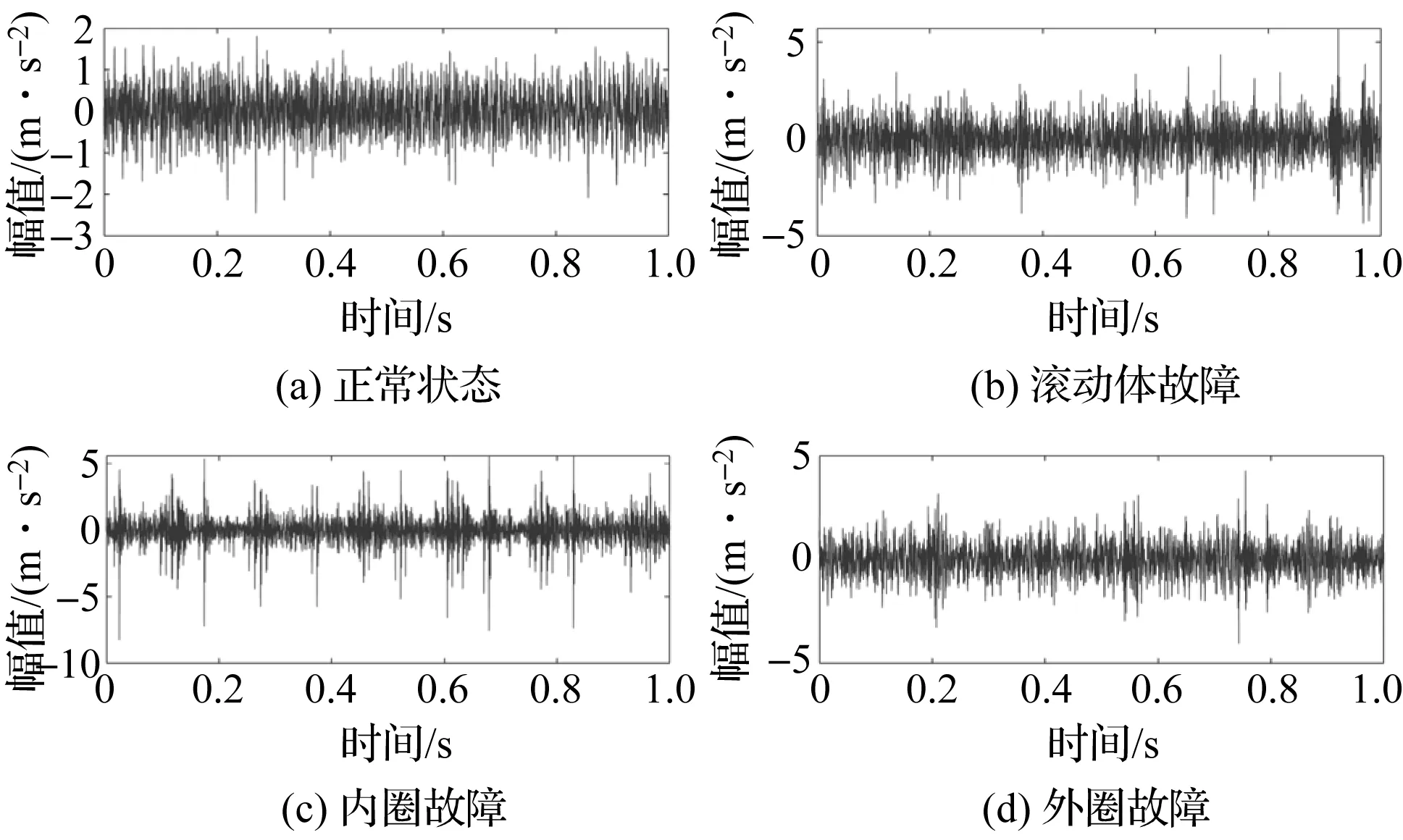
圖5 在1 200 r/min轉速下的軸承振動信號時域波形圖

實驗中,采集到在1 800 r/min轉速下3種狀態的軸承振動信號時域波形圖,如圖6所示。

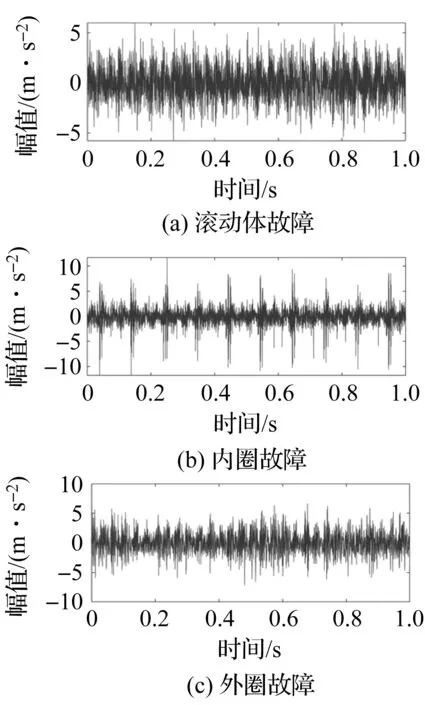
圖6 1 800 r/min轉速下的軸承振動信號時域波形圖

3 實驗結果分析

3.1 不同訓練樣本數量下各個網絡的準確率

筆者在訓練集里選擇35、70、140、210、350、420、700、1 400、2 100個訓練樣本,以及全部700個測試樣本,并將其輸入到網絡中。

為了驗證在小樣本數據下,基于SNN-LSTM網絡的方法的優越性,筆者建立與SNN-LSTM子網絡結構一致的CNN-LSTM網絡,與上述方法進行對比。同時,建立去掉長短時記憶網絡層后的SNN網絡,與上述方法進行對比;每次實驗重復10次后,取平均值得到準確率。

實驗結果如圖7所示。

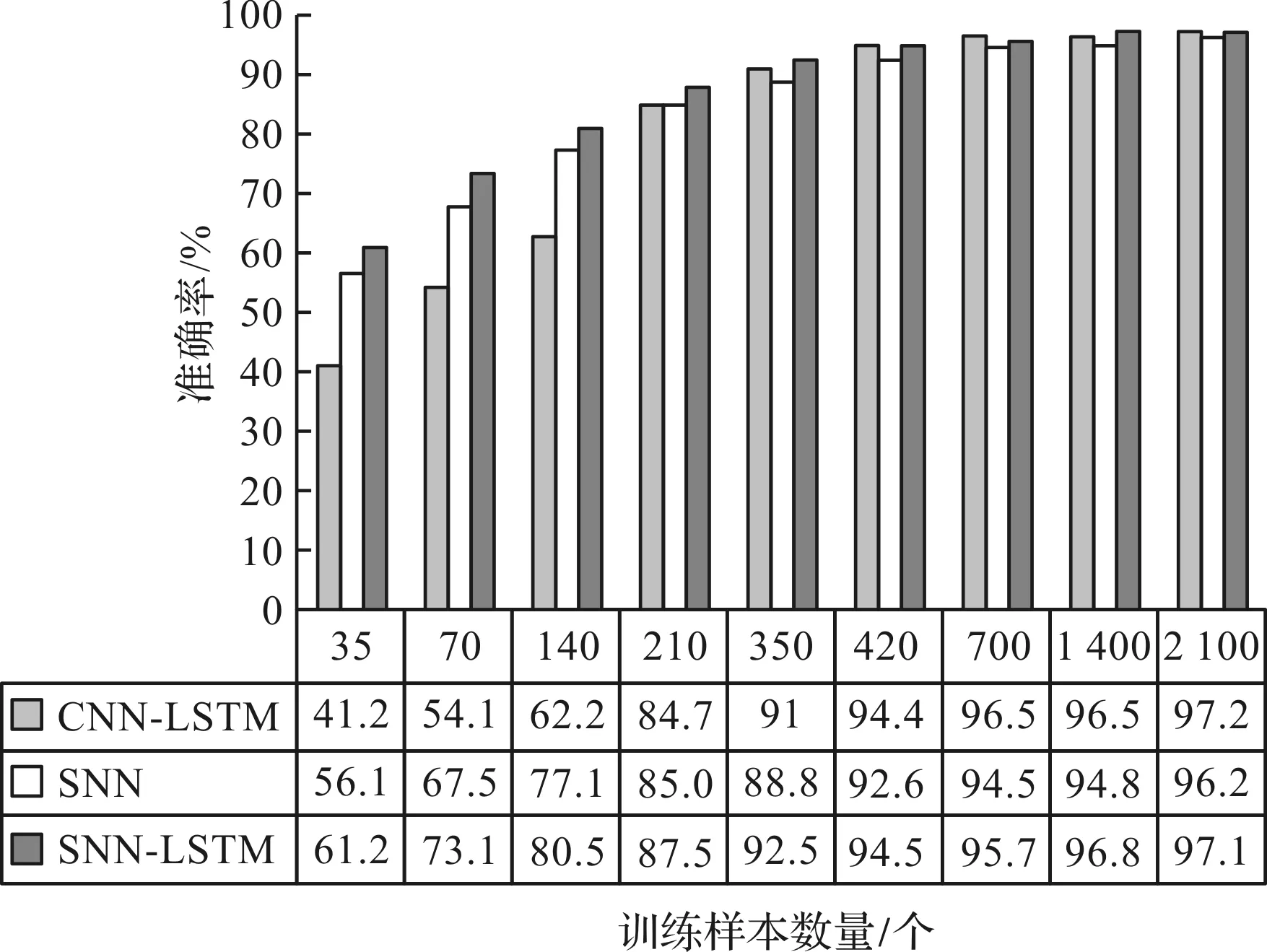
圖7 在不同訓練樣本數量下各個網絡的準確率

對比SNN-LSTM和SNN可以發現:

在不同訓練樣本數量下,SNN-LSTM的準確率都要高出SNN大概2%～4%,說明加入長短時記憶網絡層,可以提高軸承故障分類的準確率;

對比SNN-LSTM和CNN-LSTM可以看出:

當訓練樣本數量超過700個時,兩個網絡的準確率相差只有不到1%,并且二者的準確率都超過95%。隨著訓練樣本數量的增加,二者的準確率也隨著增加;

當訓練樣本數量在35～140個時,SNN-LSTM的準確率要明顯高于CNN-LSTM的準確率;

在訓練樣本數量僅為35個時,SNN-LSTM仍然有61.28%的準確率,而CNN-LSTM只有41.25%的準確率,高出20.03%。

該結果說明,SNN-LSTM在樣本數量較多的時候網絡的性能沒有多少損失;同時,在小樣本數據下比CNN-LSTM的準確率高得多。

以上結果證明,基于SNN-LSTM的方法比現有的神經網絡方法更適合于小樣本數據。

3.2 模型可視化

為了更直觀地表示神經網絡在故障診斷中的效果,筆者采用t-SNE降維的方法,對SNN-LSTM在140個訓練樣本情況下的全連接層進行降維可視化。

模型全連接層的t-SNE可視化如圖8所示。

圖8 模型全連接層的t-SNE可視化

同時,筆者給出在700個測試樣本下的混淆矩陣,如圖9所示。

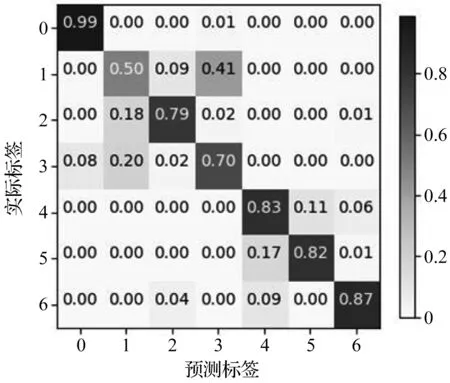
圖9 測試結果混淆矩陣

從圖(8,9)中可以看出:

SNN-LSTM故障診斷方法除了將1類中的接近一半測試樣本誤分成3類外,對于其余6個類的分類效果尚可:其中,對于0類的分類準確率最高接近100%;

對于3類的分類準確率較低為70%,其中,將20%的測試樣本誤分到1類里。

4 結束語

在小樣本數據下的軸承故障診斷中,采用基于經典神經網絡方法時,存在模型欠擬合和分類準確率低等問題,為此,筆者提出了一種基于SNN-LSTM的軸承故障診斷方法,并將其應用于小樣本數據下的軸承故障診斷中。

研究結果表明:

(1)神經網絡的輸入是原始振動信號,從而減少了經過數據處理或者數據轉化時產生的數據誤差,同時避免了相對主觀的人工提取方法;

(2)經過實驗驗證,在網絡中加入長短時記憶網絡層后,在不同訓練樣本數量的條件下,均可以提高網絡的準確率,提高2%～5%;

(3)通過對比SNN-LSTM和CNN-LSTM在不同訓練樣本數量下的準確率,可以看到:當訓練樣本數量在700～2 100個之間時,二者的準確率均超過95%,并且相差不大;當訓練樣本數量在35～140個之間時,SNN-LSTM比CNN-LSTM的準確率高出20%左右;在訓練樣本數量僅為35個時,SNN-LSTM的準確率仍有61.28%,而CNN-LSTM的準確率只有41.25%。

在后續的研究過程中,筆者將加入三一集團有限公司不對中滾動軸承數據來進行故障的分類,研究實際工程數據對上述診斷模型的影響。