一種異質圖的Lorentz 嵌入模型

蘇曉萍，查英華，曲鴻博

(1. 南京工業職業技術大學計算機與軟件學院 南京 210023；2. 南京郵電大學計算機學院 南京 210003)

信息網絡普遍存在，如經濟貿易網、社交網和計算機網絡，這些網絡的圖模型一般采用鄰接矩陣來進行表示與存儲，該矩陣具有高維、稀疏的特征，對其分析和計算的成本較高，因此，在網絡規模不斷增長的情形下，需要找到更好的方法來表示、處理圖數據。圖嵌入[1-2](也稱圖表示學習)是解決這一問題的有效方法，它的目標是：將網絡節點或邊映射到一個方便計算和存儲的低維稠密向量空間中，嵌入形成的低維向量可為多種下游數據挖掘任務提供支撐。圖嵌入的基本原則是：用較少的數據維度盡可能多地保留原網絡的拓撲結構、節點和邊屬性信息。大部分圖嵌入方法僅考慮節點、邊類型都相同的同質圖。

然而，除同質圖外，現實世界中還存在許多需要用異質圖建模的復雜系統。異質圖模型允許節點和邊的類型相異，甚至網絡類型也相異，如引文網中，節點包括：作者(A)、會議(C)、論文(P)等不同類型的對象，這些對象之間存在“參加”“發表”等語義不同的邊。相較于同質圖，異質圖的語義更豐富，對現實世界的描述更完整自然，因此，基于異質圖建模的研究近期受到了廣泛關注[3～6]。由于異質圖中節點、邊的類型不相同，原來同質圖嵌入方法不能直接應用于異質圖，需要對這一特定的網絡結構設計專門的表示方法。基于異質圖的嵌入方法在近幾年也獲得了快速發展[7-8]，異質圖嵌入的主要目標是保留原網絡的拓撲結構和語義信息，嵌入的基本原則是：網絡中“靠得越近的節點(語義相近或網絡可達)，其向量表達越相似”。異質圖嵌入方法大致可分為：基于近鄰保持的方法[9-14]和基于信息傳播[15-17]的方法。

以上異質圖嵌入方法都是將異質圖中的節點映射到人們熟悉的歐式空間，并用歐式距離來度量節點的相似性，然而，這里忽略了一個重要而根本的問題：用歐式空間表達復雜的圖數據是否合適？近期研究表明：歐式空間不能很好地表達網絡中的層次結構、無標度特性，在嵌入具有如上特征的網絡時將出現較大程度的失真[18]，嵌入失真的主要原因是：歐式空間中球的體積與半徑呈多項式增長，不具備表達數據呈指數增長的無標度特性，而在雙曲空間中，球的體積與半徑呈指數增長，這一特性使得它能很好地表達網絡呈指數增長的無標度特征[19～22]，因此將圖嵌入到雙曲空間能夠更多地保留網絡的冪率分布、強聚類、小世界等結構特征，從而獲得較歐式空間更精確的節點向量表示，為鏈路預測[23]、節點分類[24]等下游任務提供更好的精確度保證。文獻[25]研究了異質圖的雙曲嵌入問題，采用龐加萊模型實現了異質圖的雙曲嵌入，并在鏈路預測任務下證明該方法具有比歐式空間嵌入的基準算法更好的結果。

受以上研究啟發，本文提出了一種基于Lorentz模型的異質圖嵌入方法。該方法首先采用基于元路徑隨機游走的方法捕獲異質節點的鄰域以及語義信息，然后采用Lorentz 模型實現異質圖的雙曲嵌入并用雙曲距離評價節點間的相似度，最后訓練模型，使語義相近的節點的向量表達也相似。所提方法解決了以下異質圖嵌入的問題：1) 如何有效獲取異質圖的結構和語義信息；2) 如何將初始在歐式空間表達的節點語義和結構信息映射到雙曲空間；3) 如何評價雙曲空間中節點對的相似性以及如何實現在雙曲空間中目標函數的優化。

1 相關理論

1.1 異質圖的定義與實例

異質圖V定義為：G={V,E,T,?,ψ} 。 其中V和E分別表示異質圖中節點和邊的集合，任意的節點v∈V和邊e∈E分 別有映射函數 ?(v):V→TV，ψ(v):E→TE，TV和TE分 別 是 節 點 類 型 和 邊 類 型 的 集合。根據異質圖的定義可知，它允許不同(或相同)類型節點間有不同(或相同)類型的連邊，且允許節點和邊帶有屬性。它包含了多種特殊結構的圖，如：二部圖、三部圖、帶權圖等。圖1a 給出了異質圖的一個實例，圖中節點類型包括作者(A)、會議(C)、論文(P)，作者和論文之間的邊表示“發表”，會議與論文間的邊表示“收錄”，論文與論文間的邊表示“引用”。圖1a 展示了從3.2 節所述開源數據集的語義中抽取得到的異質圖，該數據集不提供作者?作者、會議?會議間的關系，因此圖中作者、會議之間沒有顯示連邊。若去掉論文?論文間的連邊，該異質圖將退化為三部圖，許多學者基于三部圖這一特殊異質圖也進行了深入研究，得到了許多有趣的結論[26]。

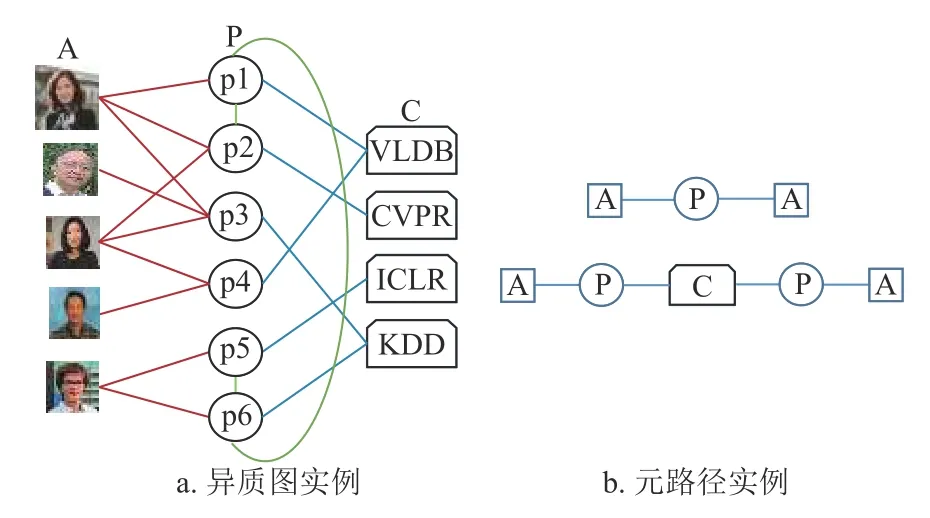
圖1 異質圖與元路徑實例

1.2 元路徑與隨機游走

1.3 基于游走序列的嵌入

隨機游走構成的節點序列可以被看作“文檔”，每個節點可以被看作“單詞”，采用自然語言處理的skip-gram 模型[28]可實現節點的嵌入。skip-gram 基本思想是采用極大似然估計來計算兩個單詞共現的概率：

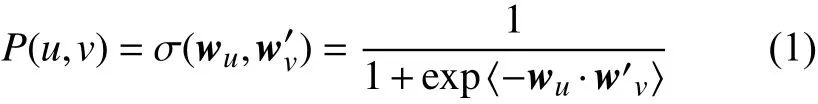
式中， σ是激活函數；wu和w′v分 別是目標詞u與其鄰居v的向量表示；skip-gram 模型對鄰居的定義是：在一定尺寸窗口內共同出現的詞， 〈wu·w′v〉表示向量的內積，該值越大則兩個單詞共現的概率就越大，模型通過優化上述概率使其最大，即可獲得每個單詞的向量表示。為計算方便，在實際應用中通常將上述的最大化問題通過取負對數轉換為最小化問題。

需要說明的是，上述模型僅能將節點嵌入到歐式空間，歐式空間在表達具有層次和無標度的網絡時將會產生失真，不利于網絡結構特征的保持，因此需要對基本skip-gram 模型進行修改，使之能夠實現雙曲空間的嵌入。

1.4 雙曲空間

1) 雙曲空間的性質

根據雙曲幾何的相關定義可知：雙曲空間是一類具有負常曲率的非歐空間，曲率k表示曲線的“彎曲”程度，我們熟悉的歐式空間曲率為零(k=0 )，雙曲空間的曲率為負(k<0，通常取k=?1) ，球面的曲率則為正(k>0 ， 通常取k=1)。定性地說，歐式空間是平坦的，而雙曲空間有一定程度的“彎曲”，因此，雙曲空間比歐式空間更“大”，具有更多“空間”。雙曲空間可以利用更少的參數來表達具有在歐式空間中同樣容量的模型。為了表達雙曲空間，研究者建立了一系列等價模型，如：Lorentz 模型、龐加萊模型、克萊因模型等，每個模型強調雙曲幾何的不同屬性。

圖2 展示了Lorentz 模型和龐加萊模型間的關系：雙曲面上任意兩點發出的射線交于Z軸上的(0,0,?1)點，射線與Z=0的龐加萊圓盤相交，此時連接雙曲面上兩點的一段圓弧被稱為Lorentz 模型的測地線，這段圓弧投影到龐加萊圓盤上則成為龐加萊模型的測地線。在有度規定義存在時，測地線為空間中兩點的局域最短路徑[29]。Lorentz 模型和龐加萊圓盤中的測地線都是“彎曲”的，其上的距離度量類似于樹形結構上兩節點間的最短路徑。圖3 進一步說明：在歐式空間看來離得很近的兩個節點在樹形結構下實際距離卻很遠，雙曲空間可以認為是一個連續的樹形結構。

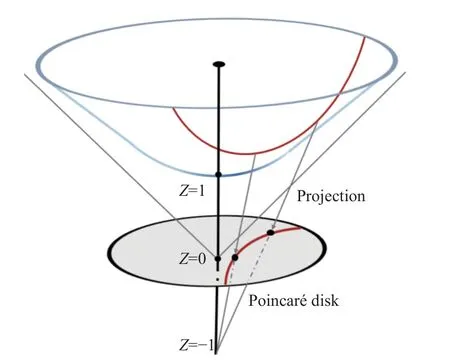
圖2 雙曲空間模型[20]

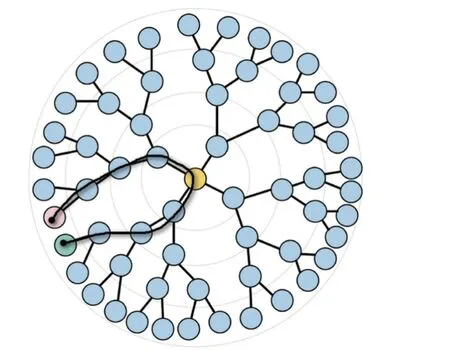
圖3 雙曲空間中的距離[30]

Lorentz 模型的幾何性質[31]決定了內積、距離等算數運算與歐式空間方法相近，且數值穩定。與此相反，龐加萊模型中計算兩個離中心節點很遠的節點內積時數值不穩定，難以優化。同時，網絡的無標度特性使大部分節點分布在龐加萊圓盤的邊界附近，節點的集中分布將導致計算機浮點數精度不足，無法正確表示邊緣節點。但龐加萊模型提供了非常直觀的可視化方法可用來解釋雙曲嵌入的結果。在代數上，Lorentz 模型和龐加萊模型是同構的，可通過數學變換將雙曲面上的點映射到龐加萊模型中。本文綜合利用兩個模型的優點，在采用Lorentz 模型實現異質圖嵌入后，將其映射到龐加萊模型進行可視化展示。

2) 洛倫茲(Lorentz)模型

定義Lorentz 標量積為：

2 異質圖的雙曲嵌入

疏，使有連接的正樣本和沒有連接的負樣本偏斜嚴重，因此對負樣本進行采樣：在非鄰居節點中隨機取若干個節點作為負樣本參與運算。模型的損失函數為：

式(5)與式(1)相似，只是內積 〈wu,w′v〉L為滿足雙曲面模型定義的Lorentz 標量積(見式(2))。對PL(u,v)取負對數使原來概率的最大化轉換成對目標函數的最小化以方便實現。

由于模型參數存在于具有黎曼流形的雙曲面中，因此反向傳播的梯度是黎曼梯度，原來歐式空間下梯度優化方法的參數更新：wti+1=wti+η?EwL(W)不再具有實際意義，因此在進行優化時需要采用黎曼梯度下降(Riemannian gradient descent, RGD)[33]。

Lorentz 模型RGD 的計算可被分解為以下3 個步驟。

1) 計算關于節點嵌入的歐氏梯度：

3 算法實現與結果分析

3.1 算法流程

算法1 給出了本文所提異質圖雙曲嵌入算法(heterogeneous graph Lorentz embedding, HGLE)的完整流程。通過執行算法1 將得到異質圖上各節點的向量表示。

算法復雜度分析：算法1 由3 個階段組成：基于元路徑約束的隨機游走序列生成、節點對采樣、梯度下降學習。其中，隨機游走階段為 |V|個節點生成m條長度為l游走序列，時間復雜度為O(|V|×m×l)；節點對采樣階段：在游走序列上為每對節點計算共同出現在窗口中的概率，其中，窗口長度為window， 時間復雜度為O(|V|×m×window×l)；采用梯度下降對skip-gram 模型進行優化，這一階段需要對每一個共現節點對進行n次負采樣，于是，噪聲節點對計算次數為O(|V|×m×window×l×n)，對每個d維向量表達的節點進行歐式梯度更新，其復雜度為O(d)，然后需將歐式梯度轉換為黎曼梯度，其復雜度為O(d)， 于是則復雜度總和就是O(|V|×m×window×l×(n+1)×2d)， 其 中m、l、 window、d、n是常數，因此算法1 的復雜度與節點總數 |V|呈線性關系，可應用于大規模異質圖。

3.2 實驗結果與分析

本文使用鏈路預測作為下游任務來驗證異質圖的雙曲嵌入效果，這是因為鏈路預測的目標是通過學習到的節點屬性、拓撲結構等信息推斷網絡中未連邊的兩節點之間產生鏈接的概率，常用于驗證圖嵌入方法的泛化能力。

算法1 得到異質圖上各節點的向量表示后，即可利用節點間的雙曲距離作為計算連邊概率的依據。實驗在CPU 為corei7，內存4 GB 電腦上采用python 實現，使用geoopt、gensim、plotly 等第三方擴展包用于雙曲空間的優化、可視化等操作。下面將詳細介紹實驗過程并進行結果分析。

1) 數據集描述

使用真實數據集評估所提HGLE 方法的效果。數據來源于公開的數據集AMiner、DBLP、ACM，這3 個數據集均為引文網，對于AMiner、DBLP，分別提取計算機科學領域學者在重要學術會議發表的相關論文(P)，ACM 是國際計算機協會主辦會議(C)論文發表情況，該數據集共涉及57 個與計算機相關主題(S)。各數據集的統計信息如表1所示。

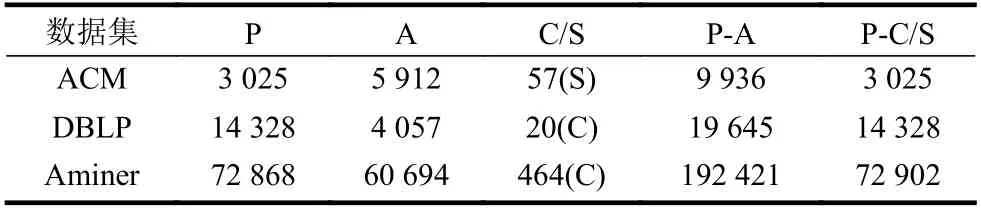
表1 數據集統計

為證明所提方法對異質圖嵌入的有效性，將它與以下基準算法在經典圖任務：鏈路預測上進行比較：

DeepWalk：經典同質圖嵌入方法，該方法基于隨機游走成功獲得了同質圖節點的嵌入表達。

metapath2vec：經典異質圖嵌入方法，該方法采用元路徑指導的隨機游走得到蘊含異質圖語義信息的游走序列，然后采用skip-gram 實現節點的嵌入。

PHomoEmb：同質圖在雙曲空間的嵌入，該方法將同質圖嵌入在雙曲面模型的雙曲空間中，證明具有層次結構和無標度特征的圖在雙曲空間獲得了更好的嵌入表達。

PHeteroEmb：異質圖在雙曲空間的嵌入，該方法基于元路徑指導的隨機游走獲得游走序列，然后采用龐加萊模型實現雙曲嵌入。

2) 模型參數

隨機游走相關參數：游走長度l=80，每節點游走次數m=50；節點嵌入相關參數：嵌入維度d分別取2、5、10、30，窗口長度 window=5，節點向量和上下文向量W和W′隨機初始化，負采樣數n=10，元路徑使用“APA”“APC(S)PA”。

3) 結果分析

實驗中，同質圖算法將所有節點和邊都看作是同一種類型，用相同策略實現節點的嵌入，異質圖算法則將分別預測“P-A”和“P-C(S)”的連邊概率，實驗結果取平均值。對每個數據集做8:1:1 劃分，80%作為訓練集，10%為驗證集，剩下10%為測試集。在訓練集上對模型進行訓練，然后用驗證集調整模型參數，獲得最小損失，然后在測試集上計算節點的連邊概率并與原數據集進行比較，使用AUC 評價鏈路預測的性能，表2 給出了實驗結果。從結果看，論文所提HGLE 方法在連邊預測上取得了較好的結果。實驗結果還顯示：面向同質圖開發的嵌入算法由于不能捕捉節點、連邊性質的差異，因此預測結果不理想；面向異質圖開發的嵌入方法，如經典的metapath2vec 算法，由于較好地保留了異質圖的結構特征和語義信息，獲得了比同質圖嵌入算法好的預測效果；又由于雙曲空間的嵌入算法更好地保留了網絡的層次特征，獲得了較歐式空間嵌入算法更好的預測精度。在此基礎上，本文所提HGLE 方法避免了計算邊緣節點距離時的數值不穩定問題，使預測性能進一步改善。

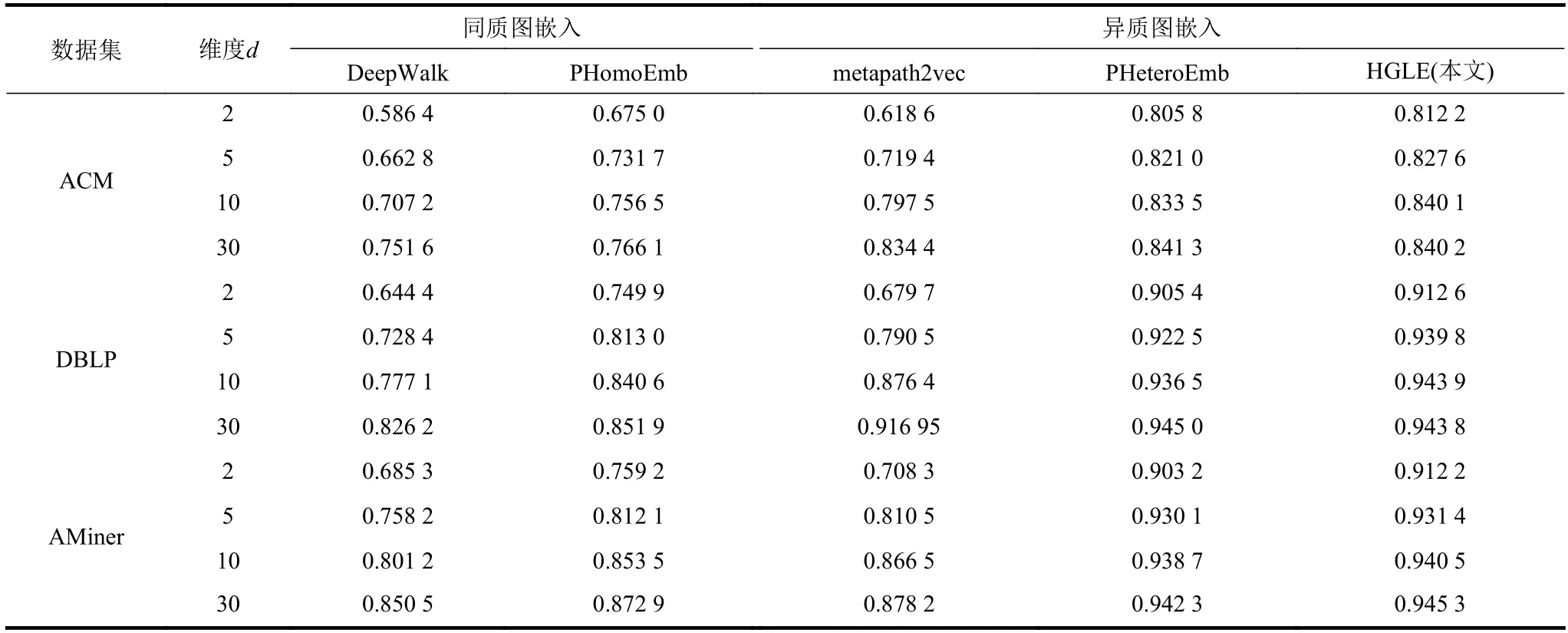
表2 各算法AUC 結果

圖4 給出了在數據集ACM 上各算法的鏈路預測精確度結果，雙曲嵌入算法在嵌入維度d=10時獲得了比歐式空間嵌入維度d=30時更好的結果，這說明基于雙曲空間的嵌入能夠用較小的嵌入維度保留更多的網絡結構和語義信息。

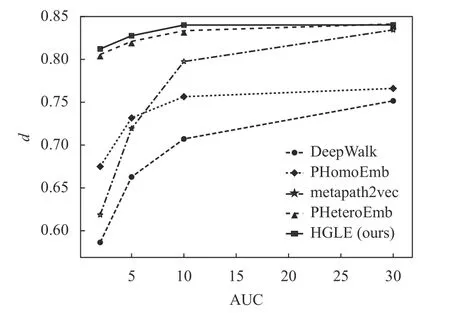
圖4 數據集ACM 上各方法鏈路預測的AUC 值

圖5 則給出了完整的AMiner 數據集嵌入在龐加萊圓盤上的投影。數據在圓盤邊沿十分密集，圓盤中心則很稀疏。利用gensim 提供的龐加萊模型計算各點與原點的距離，并用黑色圓進行了區分。黑色圓內節點與原點的距離在0～2 之間，黑色圓之外的距離在2～6 之間，這與“樹”的特征一致：層次高的節點數量少、層次低的節點呈指數增長。根據圖5 中給出的數據標簽可知：影響因子較高的學者韓家煒、Christos Faloutsos、Philip S. Yug等人均離圓心較近，說明他們是圖上的關鍵節點。經統計發現：雙曲距離在0～2 之間的作者(A)節點平均發表論文數為4.6 篇/人，是雙曲距離大于2 的作者(圖5 中黑色圓之外)的2 倍。

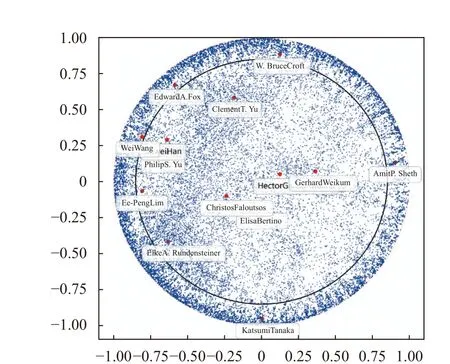
圖5 AMiner 數據集的可視化

4 結 束 語

異質圖是建模現實世界圖數據的有效手段，它蘊含更豐富的語義，對現實世界的描述也更完整自然，因此對異質圖的研究在近期受到很多關注。圖嵌入是異質圖研究的重要手段，因為圖嵌入的目標是將圖結構和節點屬性等映射到稠密、低維向量空間為下游任務提供基礎，若嵌入表達不能正確保留圖信息則后續挖掘任務無法獲得好的結果。如何為圖嵌入選擇合適的嵌入空間就成為需要認真研究的問題。由于雙曲空間中圓的周長隨半徑呈指數增長的幾何性質與圖的無標度特征恰好一致，所以可以采用雙曲空間作為異質圖的嵌入空間，但是，不同的雙曲模型具有不同的幾何性質，需要更進一步地探討和研究。另外，目前大部分雙曲空間的嵌入使用負常曲率，有一定的局限性，因為數據的復雜性使其各部呈現出不同的幾何特性，嵌入空間各處曲率應不同，曲率的選擇和學習也是具有挑戰的任務。

另外，對異質圖自身結構的理解依然沒有結束，異質圖允許不同類型節點間有連邊，也允許相同類型的節點間有連邊，同時，節點和邊帶有屬性，它包含了多種特殊結構的圖，如二部圖(或三部圖)，基于元路徑的隨機游走可以有效保留網絡拓撲和節點屬性等信息，但是元路徑的選擇需要領域知識，若元路徑由人工確定，有可能為圖嵌入引入噪聲，當異質圖退化為某種特例時，基于異質圖建模是否就比基于二部圖建模的方法好？這需要認真思考；另外，能否通過自適應的元路徑學習方法來避免元路徑人工選擇也需要深入研究。盡管本文僅介紹了異質圖對引文網的嵌入，事實上異質圖已被應用至推薦系統、信息安全和基因工程等領域，并提升了挖掘任務的性能，因此，基于異質圖的具體應用還需要進一步挖掘。

下一步研究將重點關注雙曲空間的幾何性質與網絡結構之間的關系、元路徑的選擇與學習以及異質圖嵌入在具體領域的應用。