變中有變 變中不變
劉玉兵
同學們,我們知道了一次函數y=kx+b(k、b為常數,且k≠0)的圖像是一條直線,如果把該直線經過平移、軸對稱、中心對稱變換后,你還能求出它的表達式嗎?
一、平移變換:求已知直線經過上下或左右平移后的直線表達式
例1 已知函數y=-2x+4的圖像向下平移3個單位,求平移后的函數表達式。
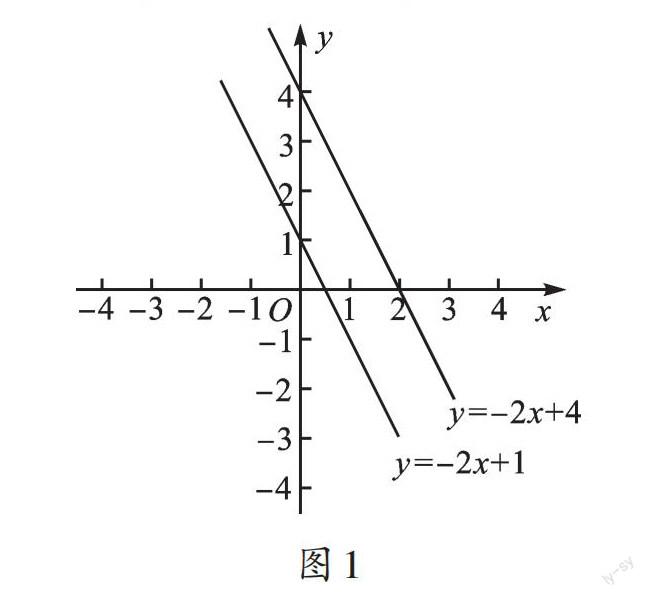
解法一:如圖1,先畫出y=-2x+4的圖像,圖像交[y]軸于(0,4);將圖像向下平移3個單位后,[k]不變,圖像與[y]軸交點變為(0,1)。設所求函數表達式為y=-2x+b,代入點(0,1),求出[b]=1,解得函數表達式為y=-2x+1。
解法二:根據“上加下減”的規律可得函數表達式為y=-2x+4-3,即y=-2x+1。
例2 已知函數y=2x+1的圖像向右平移2個單位,求平移后的函數表達式。
解法一:平移后[k]不變,圖像與[x]軸交點變為(1.5,0),求得函數表達式為y=2x-3。(圖略)
解法二:根據“左加右減”的規律可得函數表達式為y=2(x-2)+1,即y=2x-3。
二、軸對稱變換:求已知直線關于[x]軸或[y]軸對稱的直線表達式
例3 把函數y=-2x+2的圖像沿[y]軸翻折,求翻折后的函數表達式。
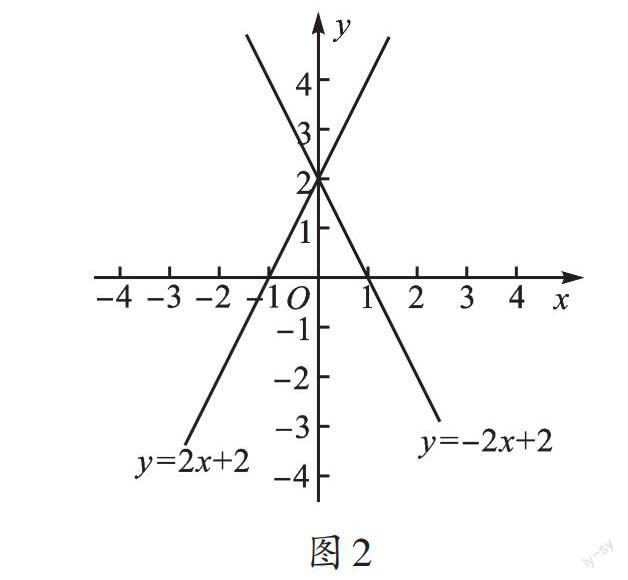
【解析】如圖2,先畫出y=-2x+2的圖像,圖像交[x]軸于(1,0),交[y]軸于(0,2);將圖像沿[y]軸翻折后,圖像與[x]軸交于(-1,0),與[y]軸交點不變。用待定系數法求出函數表達式為y=2x+2。
三、中心對稱變換:求已知直線關于某個點成中心對稱后的直線表達式
例4 求直線y=2x-3關于原點對稱的直線表達式。
【解析】直線y=2x-3交[x]軸于(1.5,0),交[y]軸于(0,-3),圖像關于原點對稱后,新圖像交[x]軸于(-1.5,0),交[y]軸于(0,3),用待定系數法可求出函數表達式為y=2x+3。(圖略)
我們發現,一次函數圖像經過平移、軸對稱、中心對稱變換后,位置在變,表達式在變,變中有變。我們可以根據兩點確定直線的定理,求出原圖像中特殊點變換后的對應點的坐標,用待定系數法確定函數表達式,此為通法,可謂變中不變。
(作者單位:南京師范大學第二附屬初級中學)

