基于自適應森林優化算法的特征選擇算法

黃君策，石 林，顧玉宛，李 寧，莊麗華，徐守坤

(常州大學 計算機與人工智能學院 阿里云大數據學院 軟件學院，江蘇 常州 213164)

0 引 言

對數據進行壓縮主要有兩種方法，數據降維是映射方法，通過主成分分析(PCA)[4]、獨立成分分析(ICA)[5]等數學方法，將高維度數據映射到低維度數據。特征選擇是挑選方法，在原數據集中挑選若干特征，組成一個滿足某種評價準則的最優特征子集[1-3]。

近年來，在特征選擇領域，通常使用元啟發式算法對搜索空間進行隨機搜索。Zhu等將遺傳算法和局部搜索算法結合提出了FS-NEIR算法[6]，該算法提出了一種新的特征評價準則，稱為領域有效信息比率(NEIR)，根據評估準則使用貪婪選擇算法進行特征子集的選擇；Xue等基于粒子群算法提出了PSO(4-2)算法[7]，在初始化策略中加入了前向后向搜索的思想，在更新機制上，將分類準確率和維度約簡兩方面考慮添加其中；Tabakhi等在對蟻群優化算法研究的基礎上，將其應用到特征選擇中，提出了UFSACO算法[8]，該算法采用濾波器方法，搜索空間被表示為一個完全連接的無向加權圖。

Ghaemi等受自然過程影響，提出了森林優化特征選擇算法(feature selection using forest optimization algorithm，FSFOA)。在進行分類時，FSFOA不需要過多的計算資源，同樣能獲得較好的分類效果；同時，FSFOA算法能保證良好的泛化性能[9]。FSFOA算法仍有一些不足：其一，FSFOA算法生成初始解空間時，隨機地從n維特征中選擇t維特征構成初始特征子集；其二，全局播種階段，FSFOA算法使用固定值設置參數GSC(global seeding change)，不能充分地發揮FSFOA算法的全局搜索能力；其三，在本地播種階段，FSFOA算法根據LSC(local seeding change)參數進行本地播種，未考慮樹的優劣情況。

針對原算法的不足，本文中提出了一種自適應的森林優化特征選擇算法(adaptation feature selection using forest optimization algorithm，AFSFOA)。①將特征權重評估算法和初始化策略相結合，提升了初始森林的質量；②參考反饋機制，提出了自適應的GSC參數選擇策略；③本地播種過程中，引入貪心算法，尋找更好的特征子集。在10個UCI中的數據集中，將AFSFOA與FSFOA以及近年來提出的其它較為高效的特征選擇算法進行比較，實驗結果表明，AFSFOA算法顯著提高了分類器的分類性能。在維度約簡方面，同樣表現較好。

1 FSFOA算法概述

受大自然森林演變過程的啟發，Ghaemi于2014年提出森林優化算法(forest optimization algorithm，FOA)，該算法能夠解決連續搜索空間問題。2016年，Ghaemi等將森林優化算法推廣到離散搜索空間，應用在特征選擇問題中，取得了不錯的效果。FSFOA算法包含初始化森林、本地播種、種群限制、全局播種以及更新最優樹等5個階段。其具體流程如圖1所示。

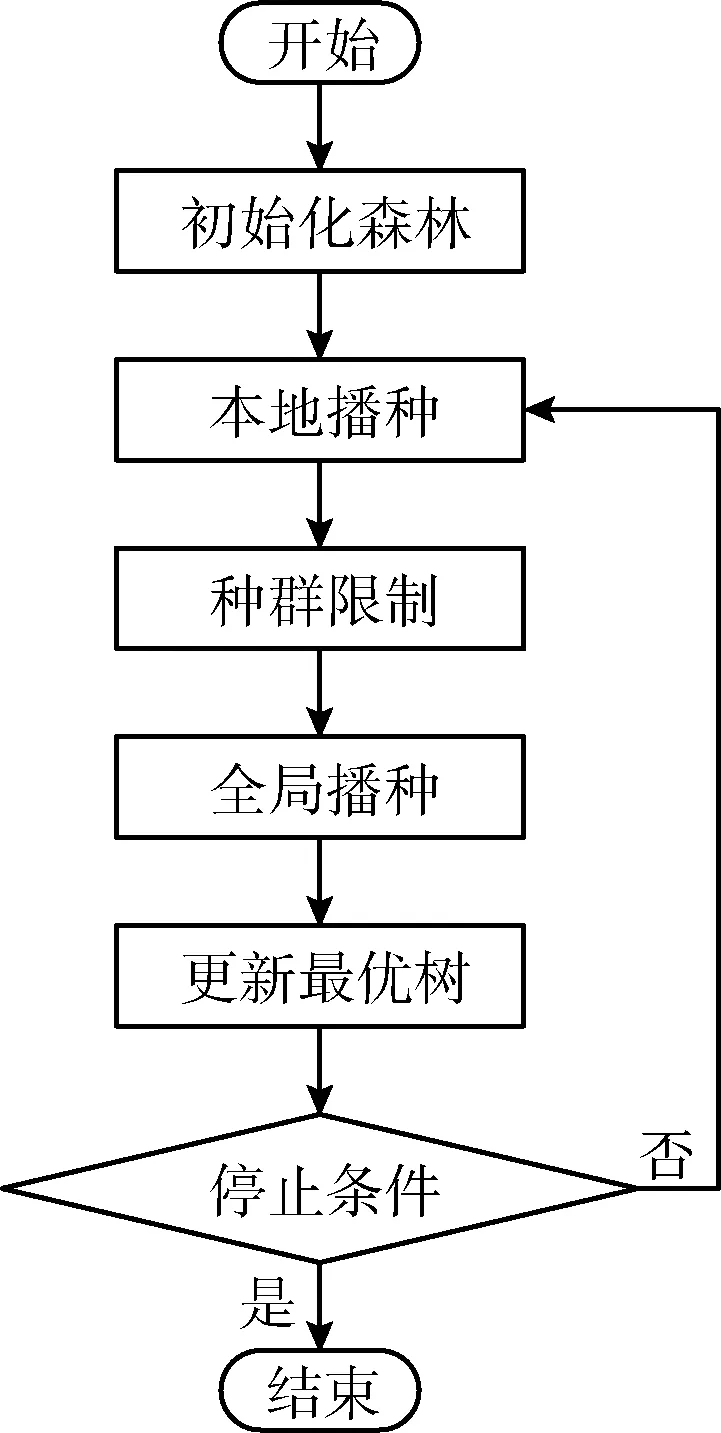
圖1 FSFOA算法流程

初始化森林(initialize trees)階段，算法生成初始森林(初始解空間)。樹由特征選擇集和樹齡(Age)構成；特征選擇集是一個n維的{0,1}向量，“0”表示在當前特征子集中，這個特征未被選擇，“1”表示這個特征被選擇，初始化階段，這些值隨機產生；樹齡是樹在解空間內存在的時間，在初始化階段，所有的樹的樹齡都被設置為0。

本地播種(local seeding)階段，算法對森林中年齡為“0”樹進行局部搜索。將Age為0的樹復制LSC(local seeding change)棵，然后隨機改變這些樹中的某一個特征選擇與否，將樹齡設置為0，放入森林中。

種群限制(population limiting)階段，算法控制森林中樹木數量。先淘汰樹齡大于年齡上限(life time)的樹木；然后依據樹適應度值(fitness)淘汰超出規模上限的樹。淘汰的樹放入候選森林。

全局播種(global seeding)階段，算法進行全局搜索。根據轉移率(transfer Rate)從候選森林中選擇部分樹，然后根據GSC(global seeding change)值，改變這些樹GSC位特征選擇與否，將樹齡設置為0后加入到森林中。

更新最優樹(update the best tree)階段，算法更新當前最優樹。算法依據樹的適應度值以及維度縮減選擇最優樹，將當前最優樹樹齡置為0后重新放入森林。

2 AFSFOA算法

2.1 初始化策略

FSFOA算法在初始化森林時，使用隨機方式生成初始解空間。隨機生成的森林中部分樹品質較低，對后續的搜索造成不利影響。本文考慮在初始化階段對特征進行一些預處理操作，生成高質量的初始解。

特征的最佳子集高度包含與標簽具有強相關性的特征，在初始化時，選中強相關特征能夠有效提升初始解空間的質量。與標簽相關性較弱的特征在分類時，對分類的貢獻較小，引入最終最佳特征子集的可能性較小。參考最近的相關研究[10]，本文提出了一種結合了特征相關性的初始化策略。初始化階段，首先對所有特征的特征相關性ω進行評價，依據一定的選擇策略選擇特征集中強相關的特征作為優質特征。在生成初始森林時，隨機生成一些樹，然后將這些樹的優質特征全部選中。從而構建出對于后續算法搜索過程友好的優質樹。

本文使用了特征權重評估算法[10]對特征相關性ω進行計算，特征權重評估算法在計算特征權重時，不僅考慮特征之間相關性，也會考慮特征和類別之間的相關性。算法從數據集D中隨機選擇一個樣本xi，搜索xi的同類最近鄰樣本xi(s)和異類最近鄰樣本xi(d)。然后調整特征對應的同類、異類差異度值，并根據特征差異度相應地調整特征權重。迭代后得到所有特征的相關性權重。

在樣本x1與x2上，兩者在特征維度fj上的差異度diff(x1,x2,j) 為

(1)

xi選擇r個同類最近鄰和異類最近鄰調整特征fj的權值

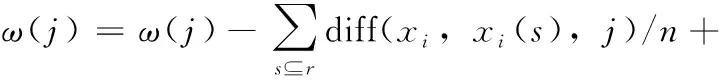
(2)

特征權重評估算法:

輸入：數據集D，子集維數n。

輸出：特征權重ω(1,…,n)。

(1) 初始化數據集D中特征權重ω(1,…,n)=0；

(2) for i = 1 tondo

(3) 隨機獲取一個實例xi；

(4) 搜索xi的同類最近鄰xi(s)和異類最近鄰xi(d)；

(5) for j=1 tondo

(6) 根據權重調整式(2)調整權重ω(j)

(7) end for

(8) 更新特征權重ω(1,…,n)

(9) end for

對特征進行挑選時，特征的權重越大，表示該特征的分類能力越強，反之，表示該特征分類能力越弱。對于優質特征的選擇，參考文獻[10]，如果特征的相關性滿足

(3)

則將特征視為優質特征。其中α是接受不相關特征被誤認為相關特征的概率，m為樣本的實例個數。

2.2 自適應全局播種策略

全局播種階段，算法修改GSC個特征的選擇與否，GSC參數控制了樹木形態的改變。固定的GSC參數限制了樹木形態的調整，無法達到全局搜索以跳出局部最優的目的。本文改進GSC參數的生成策略，充分利用算法的全局搜索機制，跳出局部最優，搜索最優特征子集。

在候選森林中，樹的形態并不一致：部分樹生成時相對劣質，對于這些劣質樹，其對應的特征集合與最優特征子集差別較大，與分類標準的要求并不相符，需要對這些樹的特征集合做出較多改變；部分樹自身特征集合相對優秀，其對應的特征集合趨近于最優解，這些樹的特征集合需要的改變較少。

本文改變GSC參數值的生成方式，由固定參數值改為自適應生成GSC參數值。由自動控制理論的啟發，本文引入了反饋調節機制，根據樹的適應度值(樹的質量)“Fitness”確定GSC參數值。樹的適應度值為當前樹確定的特征子集分類準確率。劣質樹調整較多特征的選擇與否，設置較大的GSC值；優質樹調整較少特征，設置較小的GSC值。同時將全局播種策略與局部播種策略區分，設置了GSC參數的上下限。

自適應全局播種策略中，GSC參數值是樹適應度值的函數

numGSC=f(Fitness)

(4)

對樹質量進行評判時，不僅需要考慮當前樹的質量，也要考慮理想樹的質量，才能對樹質量做出恰當的評判。本文對當前樹質量Fitnessnow和理想最優樹質量Fitnessbest進行比較，確定當前樹的質量。在確定樹的質量時，如果Fitnessnow和Fitnessbest兩者差距較大，保守地對樹質量做出評價；差距較小時，激進地對樹做出評價。由于理想最優樹的適應度值難以確定，本文使用當前最優樹來近似替代理想最優樹。樹質量函數為

(5)

得到當前樹的質量后，需要將其映射到需要修改的特征個數。當前樹的質量與需要修改的特征個數之間是呈正比關系的。即

numchange∝Fitness

(6)

確定GSC參數值時，從當前數據集的特征個數n得到需要修改的特征個數。首先控制全局播種過程中特征改變個數的范圍，設定參數GSC的上界為0.5n；GSC值為1時，全局播種的搜索范圍和本地播種一致，全局播種則退化為本地播種，為了將全局播種過程與本地播種相區別，設定GSC值的下界為2。則2≤numGSC≤0.5n。 由此，GSC參數值的確定公式如下

(7)

全局播種過程本質是一種全局搜索策略，自適應調整的GSC值，能充分利用全局播種輔助尋優的特性，擴大全局播種的搜索范圍，避免算法陷入局部最優情形。更容易找到相對優秀的搜索子空間，收斂到最優解。

2.3 貪心搜索策略

本地播種過程中，FSFOA算法對所有樹齡為“0”的樹進行局部搜索，限制了算法尋優性能。本文對本地播種過程做出改進，充分利用局部搜索效果，尋找最優特征子集。

本地播種過程中，年齡為“0”的樹形態不一致。劣質樹的特征和理想最優樹的特征差異度較大，對其進行局部搜索時，改變個別特征，無法尋找到優質樹；優質樹的特征子集和理想最優特征子集相差較小，對其進行局部搜索時，搜索的次數越多，尋找到更好特征子集的可能性越大。

本文對本地播種策略略作調整，對局部搜索樹增加了更多的限制，同時增加了局部搜索的搜索范圍。

本文在選擇局部搜索樹時，首先選中森林中樹齡為“0”的樹，然后根據樹的質量進行進一步選擇。受貪心策略的啟發，在進一步挑選時，選擇優質樹進行后續的局部搜索過程，減少劣質樹的局部搜索，減少森林中的劣質樹。僅選擇適應度值最高的樹，森林中樹缺少多樣性，算法可能陷入局部最優情形，選擇森林中一半的樹可以保證森林里樹的多樣性。判斷樹的質量時，將樹齡為“0”的樹根據其適應度值從高到低排序，適應度值排名前一半的樹標記為優質樹，繼續后續的局部搜索過程；適應度值排名后一半的樹則為劣質樹，不進行后續的局部搜索。在選擇樹時，選擇原算法一半的樹進行后續局部搜索過程。

對優質樹進行局部搜索時，擴大其搜索范圍。FSFOA算法在局部搜索時，其搜索范圍是由LSC參數值控制的。算法的LSC值與數據集特征個數n相關，其值為

(8)

在選擇局部搜索樹時，本文選擇原算法一半的樹進行后續局部搜索過程；在搜索時，本文將搜索范圍擴大一半，將LSC值設為

(9)

在能夠搜索到更好的特征子集同時，也保證了算法的運行效率。

本地播種過程是一個局部搜索過程，是一個“優中尋優”的過程。調整后的本地播種過程，充分利用了局部搜索“優中選優”的特性，去除了對劣質樹的局部尋優，增加了優質樹的尋優范圍，更容易收斂到最優特征子集。

3 實驗結果與分析

本文實驗平臺為一臺CPU為Intel i7-6800K、操作系統為Linux(Ubuntu 16.04)的計算機。實驗使用語言為python3，此外還使用了著名的機器學習工具包scikit-learn。

3.1 數據集

本文在10個不同規模的UCI數據集上進行了對比實驗。根據文獻[9]，按照數據集規模，選擇了特征數量在[0,19]之間的6個低維度數據集(Glass、Wine、Heart、Cleveland、Vehicle、Segmentation)；特征數量在[20,49]之間的2個中維度數據集(Dermatology、Ionosphere)；特征數量在[50,∞]之間的2個高維度數據集(Sonar、SRBCT)。選擇不同維度的數據集，能夠看出算法在不同情形下的表現。數據集的具體信息見表1。表中n為數據集總的特征個數，m為數據集實例個數，labels為數據集類別數目。

表1 數據集概述

3.2 評價指標

本文在對實驗結果進行對比時，使用了兩種評價指標對算法進行評價。

第一種評價指標為算法的分類準確率CA(classification accuracy)，分類準確率反映最優特征子集在分類器上的表現。其具體定義如下

CA=CC/AC

(10)

其中，CC表示了能夠正確分類的實例數，AC(all classifica-tion)則是參與分類的實例總數。

第二種評價指標為算法的維度約簡率DR(dimensio-nality reduction)，維度約簡率是對最優特征子集特征個數的評價。其具體定義為

DR=1-(SF/AF)

(11)

其中，SF(selected features)是在特征集中被選擇的特征個數，AF(all features)是數據集的特征總數，即n。

3.3 參數設置

實驗過程中，AFSFOA算法的參數設置規則為：參數設置方法未改進，依據參考文獻[9]中的設置方法，設為與FSFOA算法相同的參數值，確保實驗公平性；參數設置方法有調整，依據本文方法重新設定參數值。未做修改的參數設置中，固定參數的設置由表2給出。

表2 AFSFOA算法固定參數信息

3.4 實驗結果對比分析

本文在進行對比實驗時，在比較AFSFOA算法與原算法FSFOA表現的基礎上，拓展了算法的比較范圍，選擇部分近年來表現出色的特征選擇算法進行對比。

進行比較的特征選擇算法包括過濾式特征選擇算法和嵌入式特征選擇算法。過濾式特征選擇算法有：FS-NEIR、SVM-FuzCoc[12]和NSM[13]，這類算法使用具體評價準則給每個特征打分，運算效率較高。嵌入式特征選擇算法為UFSACO和PSO(4-2)，這類算法構建學習器，根據預測精度對特征子集進行評價，分類準確率較高。

在進行對比實驗時，主要使用了DT分類器和KNN分類器。為了保證實驗的可靠性，部分實驗使用了10折交叉驗證。實驗結果見表3。

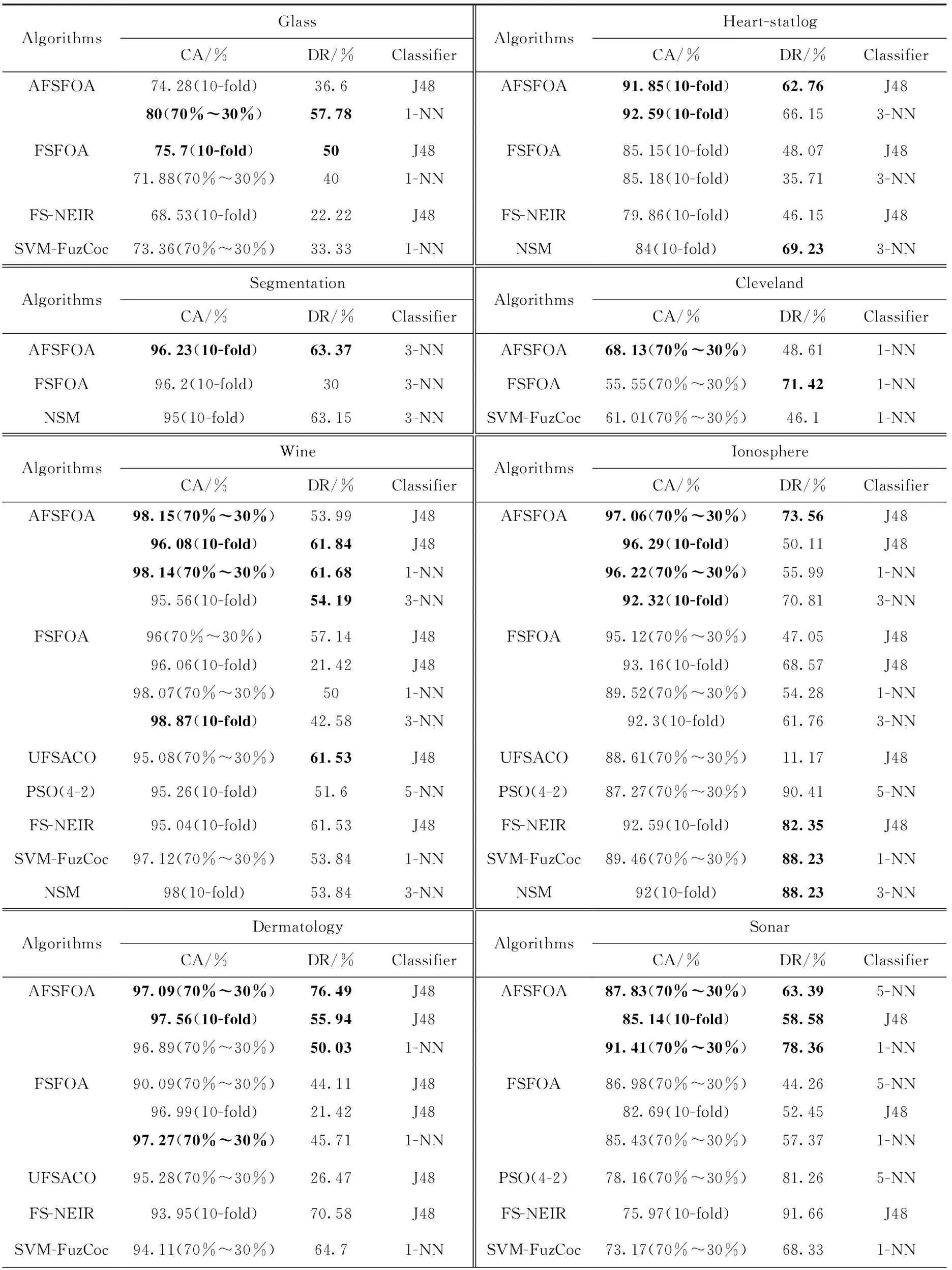
表3 實驗結果

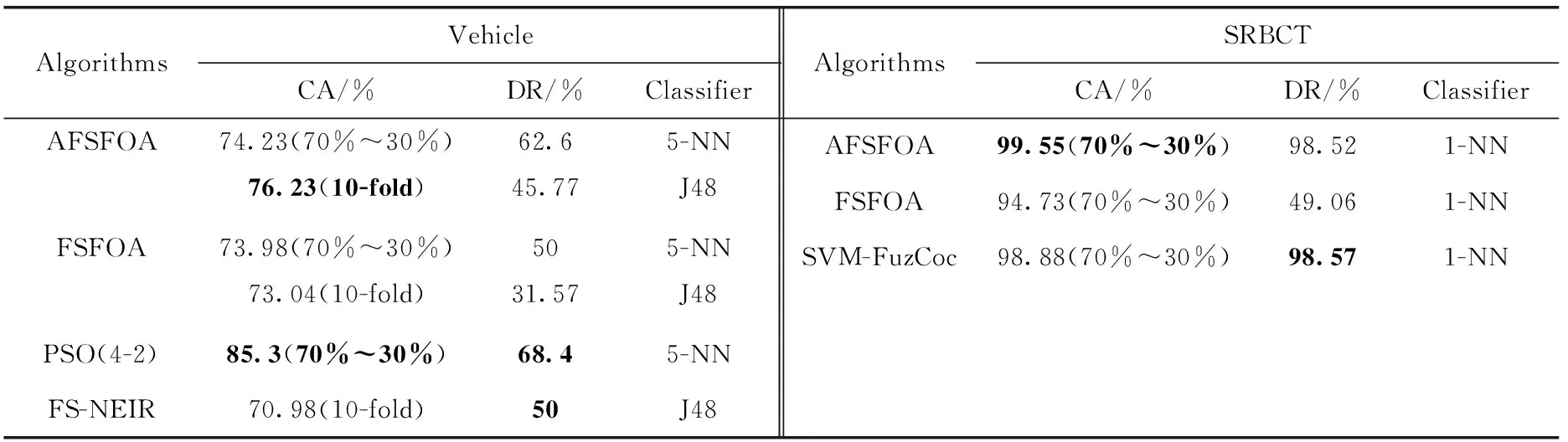
表3(續)

比較AFSFOA算法在不同分類器中的表現，在Glass、Heart-statlog和Sonar這些數據集中，算法在KNN分類器中的表現優于DT分類器。在特征選擇后，最優特征子集已包含所有有效信息。KNN學習器在分類時，使用了所有特征來進行分類；而DT學習器分類時，會丟棄少量信息。因此，KNN學習器的分類精度較DT分類器高。

將AFSFOA算法與FSFOA算法實驗結果對比，可以看到改進后的AFSFOA算法確有成效。在Sonar、Heart-statlog、Segmentation、SRBCT等數據集上，AFSFOA算法在不同的分類器中，分類準確率以及維度縮減率都有提高；在Cleveland、Ionosphere等數據集上，AFSFOA算法在不同分類器上的分類準確率有明顯提升；在Vehicle、Wine、Glass、Dermatology這些數據集中，AFSFOA算法在部分分類器中分類性能略低于FSFOA算法，但維度縮減率提升較多；其中Wine數據集在使用3-NN分類器時，分類準確率相差較大，準確率低了約3%，但維度約簡提升了約20%。

比較在不同維度數據集下，AFSFOA算法的表現。在高維度的兩個數據集Sonar和SRBCT中，AFSFOA算法較FSFOA算法有著明顯的提升，分類準確率均提高了5%～10%，同時維度約簡也有著明顯的提升；在中維度數據集Ionosphere、Dermatology中，除Dermatology在1 NN分類器中的表現略遜于FSFOA算法外，其它分類器上，本文算法仍有著較好的表現；低維度數據集中，AFSFOA算法在絕大多數的分類器中表現良好，僅有部分分類器較FSFOA算法未有提升，但在這些分類器中，維度約簡有著明顯的提高。對不同維度的數據集進行比較，可以看出AFSFOA算法在中高維度的數據集中表現優異，而在低維度數據集中，表現同樣具有競爭力。對于不同維度的數據集，AFSFOA算法都能得到較好的結果，具有良好的泛化能力。

與其它算法進行對比時，AFSFOA算法在分類準確率上仍有很強的競爭力。使用相同的學習器對數據集訓練，僅在Vehicle數據集中，使用5-NN分類器時，表現不如PSO(4-2)算法，在分類準確率上，AFSFOA算法的準確率比PSO(4-2)算法低約10%；在其它數據集中，AFSFOA算法仍占有優勢。

在維度約簡能力上，和FSFOA算法相比，AFSFOA算法的維度約簡能力有著明顯的提升，但和其它算法相比，AFSFOA算法表現一般。但在兩個高維數據集Sonar和SRBCT中，與同類算法對比，AFSFOA算法的維度約簡能力均能達到最高的水準。在Sonar和Segmentation這兩個數據集中，和FSFOA算法以及其它算法對比，AFSFOA算法在保持分類準確率的同時，有著優秀的維度約簡能力。在Glass和Cleveland這兩個數據集中，本文算法的維度約簡率不如FSFOA算法，且差距較大，且在Glass數據集中，本文算法在分類準確率上上同樣低于FSFOA算法。和其它算法的維度約簡能力相比，AFSFOA算法仍然有著不小的進步空間；在Vehicle和Ionosphere這兩個數據集中，AFSFOA算法的維度約簡與其它算法相比均有較大差距。

4 結束語

通過對森林優化特征選擇算法(FSFOA)的研究與分析，本文針對其不足之處做了3點優化。在FSFOA算法的初始化階段，本文加入了特征權重評估算法，優化搜索起始點，便于后面算法進行高效搜索；在全局播種階段，本文加入了參數自適應生成策略，通過對樹“Fitness”值的分析，自動生成全局搜索參數(GSC)；在算法的局部播種階段，加入了貪婪策略，增加對年齡為“0”的優質樹的局部搜索。將AFSFOA算法在10個UCI數據集中進行測試，并與其它特征選擇算法進行對比，實驗結果表明，AFSFOA算法顯著地提高了分類準確率；同時在部分數據集中，能夠生成維度更少的特征子集。