基于雙排隊系統的軟件可靠性增長模型
周 楠,李福川+,宣 萱
(1.中國航天科工集團第二研究院 七〇六所,北京 100854; 2.中國航天科工集團第二研究院 重點型號部,北京 100854)
0 引 言
基于排隊論的SRGM作為軟件可靠性建模[1,2]研究中的重要分支,更準確地描述出由檢測和修正兩個子過程構成的測試工作[3]中故障所經歷的歷程,在可靠性的分析與評估方面展現出良好的能力。國內外研究者使用無限服務臺排隊(infinite server queuing,ISQ)模型建模軟件測試過程,并逐步引入不完美排錯和移動點等影響因素。但研究發現服務臺數量是無限的假設,違背了真實的測試過程,通過修正ISQ模型的假設條件,考慮到時間延遲現象,提出有限服務臺排隊(finite server queuing,FSQ)模型。隨著研究的深入,進一步挖掘隊列平均長度、平均等待時間等排隊論的核心內容,提出擴展的FSQ模型[4-8]。目前,隊列模型主要對故障修正過程進行建模,忽略了軟件從交付到檢測過程中存在的排隊等待現象。
針對上述問題,本文分析了資源相互獨立的故障檢測過程與故障修正過程,提出一種將排隊論同時應用在檢測與修正過程的雙排隊系統模型,并在建模中考慮不完美排錯現象,實現對修正過程中可能破壞程序內部的邏輯結構,引入新故障現象的定量描述,從而提高模型對軟件可靠性評估與預測的精度。通過對比實驗驗證模型的性能,同時對未來的發展趨勢進行了展望。
1 相關工作
當前的軟件可靠性增長模型大多數都存在著與真實軟件測試過程不相符合的假設條件[5,9,10],如完美調試、故障立即被修正以及測試工作量統一考慮等。而在實際的測試過程中,檢測故障的工作通常由專業的軟件評測人員來完成,開發人員則根據檢測過程反饋的故障信息對程序代碼進行修改,完成修正階段的工作。兩組不同的人員花費不同的CPU時間完成各自的任務,是資源相互獨立的兩個過程,因此需要將檢測過程和修正過程消耗的工作量進行區分,建立各自過程的函數模型。
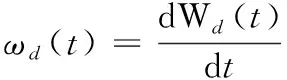
ωd(t)=ξω(t)
(1)
ωc(t)=(1-ξ)ω(t)
(2)
式中:ξ表示在t時刻的規模比率,在這里設置為常數。
測試資源作為一個綜合性的影響因素,通常用執行的測試用例數目、消耗的CPU時間以及測試人員的數量等信息來度量。基于學習因素和軟件結構的綜合影響,在測試的初期,測試工作量通常會迅速增長,而隨著過程的進行,增長速度會減緩,最后趨于平穩,呈現出一種S型變化趨勢[11,12]。考慮到測試工作量這一變化特點,本文在建模過程中選用了變形S型TEF,如式(3)所示
(3)
式中:W表示最終消耗的總測試工作量;α表示測試工作量消耗率;A為一個常量。
將式(3)代入式(1)和式(2)后再對t進行積分,可以得到故障檢測工作量函數以及故障修正工作量函數,如式(4)和式(5)所示
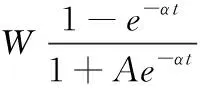
(4)
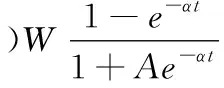
(5)
2 基于雙排隊系統的軟件可靠性增長模型
2.1 基本假設
(1)軟件中失效事件隨機發生,故障檢測過程與修正過程服從非齊次泊松過程(non-homogeneous poisson process,NHPP)[9],設到t時刻累計檢測出的故障數N(t)服從期望函數為m(t)的NHPP分布,滿足t=0時, m(0)=0。 可以得到
(6)
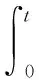
(7)
式中:λ(τ) 表示τ時刻軟件的失效強度函數。
在 (t,t+x] 時間間隔內不發生軟件失效的概率,即軟件可靠性為
R(x|t)=P{N(t+x)-N(t)=0}=e-m(t+x)+m(t)
(8)
(2)軟件故障之間互不干擾且失效行為均是由未檢測出的故障引發的[4]。
(3)在 (t,t+x] 時間區間內,累積檢測到的故障數量與t時刻剩余未檢測出的故障數量成正比,比例系數為故障檢測率[4,9]。
(4)在 (t,t+x] 時間區間內,累積修正的故障數量與t時刻檢測到但未被修正的故障數量成正比,比例系數為故障修正率[9]。
(5)引起軟件失效的故障最終都會被修正,且故障檢測過程在修正故障時會繼續執行,故障的修正過程不會對故障的檢測造成影響[4]。
(6) 使用兩個不同的FSQ模型分別對故障檢測活動以及故障修正活動進行描述,其中檢測過程模型滿足批量到達,修正過程模型滿足NHPP到達。
(7)故障修正過程中,會引入新的故障且故障引入率為k[4]。
2.2 建模過程
2.2.1 故障檢測過程
B(t)表示某個故障在(0,t]時間內被檢測到的概率,包括兩個部分:一部分是假設故障在0時刻到達,而且有空閑的檢測人員對其進行檢測,并在(0,t]時間內被檢測到;另一部分則是假設有限數量的檢測服務人員都在工作中,故障在0時刻到達,并沒有立即得到檢測,而是在隊列中等待一段時間(0,y]后,才在(y,t]時間內被檢測到,如圖1所示。

圖1 在0時刻到達的故障在(0,t]內被檢測到
根據乘法公式,B(t)表示為

(9)
式中:Ta表示故障被送達的時間點;Tb表示檢測故障時所用的時間;Te表示故障等待檢測時所用的時間。
軟件交付到故障檢測人員手中時也就意味著故障被送達,則令 P{Ta=0}=1, 代入式(9)可得

(10)
式中:D(t)表示不存在排隊現象時服務人員檢測故障所用時間的累積分布函數; D(t-y) 表示存在排隊現象時服務人員檢測故障所用時間的累積分布函數;L(y)表示故障在隊列中等待檢測時所用時間的累積分布函數。
在實際的故障檢測過程中,需要考慮到軟件設計的復雜度、故障檢測人員的檢測水平、檢測工作量以及檢測環境等因素對檢測效果的影響。其中故障檢測工作量隨測試時間的變化情況對軟件的可靠性增長曲線有顯著影響,為了全面和準確地描述軟件故障檢測過程,在故障檢測過程中引入故障檢測工作量。另一方面,故障檢測工作量對檢測等待延遲也有一定的影響,隨著投入的故障檢測資源的增加,檢測等待延遲會減小。因此,在分析檢測等待延遲時,也需要考慮故障檢測工作量。由于指數分布經常被假定為排隊論中的服務時間分布[13,14],故假設故障檢測時間的分布函數如式(11)所示
D(z)=1-e-ρdWd(t)+ρdWd(t-z)
(11)
故障檢測等待時間的分布函數如式(12)所示
L(z)=1-e-μdWd(y)+μdWd(y-z)
(12)
式中:ρd表示每單位故障檢測工作量的故障檢測率;μd表示每單位故障檢測工作量的檢測等待率。
根據式(11)和式(12)可得
D(t)=1-e-ρdWd(t)
(13)
D(t-y)=1-e-ρdWd(t)+ρdWd(y)
(14)
L(y)=1-e-μdWd(y)
(15)
將式(13)~式(15)代入式(10),可得
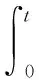
[1-e-ρdWd(t)+ρdWd(y)]dy
(16)
對式(16)求導得故障檢測率函數,如式(17)所示
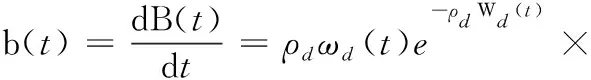
(17)
其中
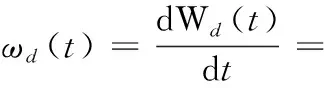
(18)
根據假設條件(7),考慮到故障修正過程存在引入新故障的現象,可以建立如下的微分方程
(19)
式中:a(t)表示隨t發生變化的隱藏的故障總數,包括了初始故障數和引入故障數;a表示初始故障總數。
代入初始條件md(0)=0, 可得如下故障檢測過程模型
(20)
2.2.2 故障修正過程
P(t)表示某個被檢測到的故障在 (0,t] 時間內被完全修正的概率,包括兩個部分:一部分是假設故障通過檢測過程在x時刻被發現,而且有空閑的修正人員對其進行修正,并在 (x,t] 時間內被完全修正;另一部分則是假設有限數量的修正服務人員都在工作中,故障在x時刻被檢測到,并沒有立即得到修正,而是在隊列中等待一段時間 (x,y] 后,才在 (y,t] 時間內被完全修正,如圖2所示。

圖2 在x時刻檢測到的故障在(x,t]內被修正
根據乘法公式,P(t)表示為

(21)
式中:Td表示故障被檢測到的時間點;Tc表示修正故障時所用的時間;Tq表示故障等待修正時所用的時間。
對式(21)做進一步變換,可得

(22)
式中: G(t-x) 表示不存在排隊現象時服務人員修正故障所用時間的累積分布函數; G(t-y) 表示存在排隊現象時服務人員修正故障所用時間的累積分布函數; F(y-x) 表示故障在隊列中等待修正時所用時間的累積分布函數。
在x時刻故障被檢測到的概率為b(x),代入式(22)可得

(23)
實際的故障修正過程同檢測過程一樣會受到多種因素的影響,同樣使用結合故障修正工作量的指數分布作為服務時間分布,故假設故障修正時間的分布函數如式(24)所示
G(z)=1-e-ρcWc(t)+ρcWc(t-z)
(24)
故障排錯等待時間的分布函數如式(25)所示
F(z)=1-e-μcWc(y)+μcWc(y-z)
(25)
式中:ρc表示每單位故障修正工作量的故障修正率;μc表示每單位故障修正工作量的排錯等待率。
根據式(24)和式(25),可得
G(t-x)=1-e-ρcWc(t)+ρcWc(x)
(26)
G(t-y)=1-e-ρcWc(t)+ρcWc(y)
(27)
F(y-x)=1-e-μcWc(y)+μcWc(x)
(28)
將式(26)~式(28)代入式(23)可得

(29)
根據假設條件(4),可得
(30)
式中:mdt表示到t時刻為止,運用故障檢測過程模型估計出的累積故障數量。
代入初始條件mc(0)=0, 可得如下故障修正過程模型
mc(t)=mdt[1-e-P(t)]
(31)
3 實驗分析
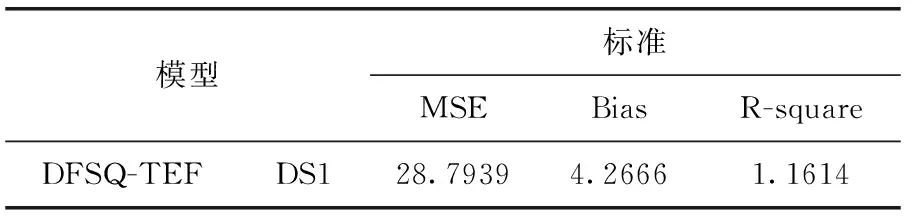
為了評估和驗證模型的擬合效果以及預測能力,本節給出了4個具有代表性的模型評價標準,同時舉例介紹了模型的參數估計方法,并根據已經公開發表的,在系統開發過程中所搜集到的4個軟件失效數據集進行仿真實驗,最后對模型的復雜度進行了分析。參與比較的所有模型見表1。

表1 參與比較的模型
3.1 模型的評價標準
模型擬合能力比較標準:
(1)均方誤差
MSE是一個平均值,反映模型的輸出值與累積故障數的真實值之間的偏差程度。MSE值越小,說明模型的擬合能力越好。
式中,n表示失效數據集中記錄的樣本條數;m(ti)表示到時刻ti為止累積檢測或修正的故障數的估計值;mi表示到時刻ti為止累積檢測或修正的故障數的真實值。
(2)Bias評價標準
Bias表示累積故障數的估計值和真實值之間的誤差,反映模型本身的精確度。Bias值越小,說明模型的擬合能力越好。
(3)回歸曲線方程的相關指數
R-square值距離1越近,說明模型的擬合能力越好。
模型預測能力比較標準:
(4)相對誤差
一般會將RE值制成RE圖,RE圖中接近x軸的預測點越多,說明模型的預測能力越好。
3.2 失效數據集
失效數據集是對軟件可靠性增長模型進行評估與預測的基礎,多以日歷時間作為故障檢測與修正的時間周期。記錄項依據軟件公司對數據的需求以及收集方式的不同存在差異,包含的基礎信息有累積檢測的故障數量和消耗的CPU時間,部分含有累積修正的故障數量,更全面的會有故障類型等信息。失效數據的質量好壞會對實驗結果準確與否產生巨大影響,實驗中選用的4個失效數據集是已經公開發表,并在軟件可靠性領域得到廣泛應用的,因此可以保證數據的有效性和準確性。
DS1:RADC-T1數據集[18]
RADC-T1失效數據集是羅馬空軍開發中心發布的實時指令控制應用系統的失效數據,測試周期為21周,軟件測試人員花費300.1CPU小時,共檢測到并糾正了136個故障。
DS2:Okumoto數據集[19]
Okumoto失效數據集是K.Okumoto發布的Alcate/Lucent公司的失效數據,測試周期為56周,軟件測試人員花費6423.5CPU小時,共檢測出124個故障。
DS3:Ohba數據集[19]
Ohba失效數據集是Ohba發布的PL/1項目的失效數據,測試周期為19周,軟件測試人員花費47.65CPU小時,共檢測出328個故障。
DS4:Wood數據集[12]
Wood失效數據集是Alan Wood在1996年發表的一篇論文中收集的某個項目的失效數據,測試周期為20周,軟件測試人員花費10000CPU小時,共檢測出100個故障。
3.3 模型參數的擬合方法
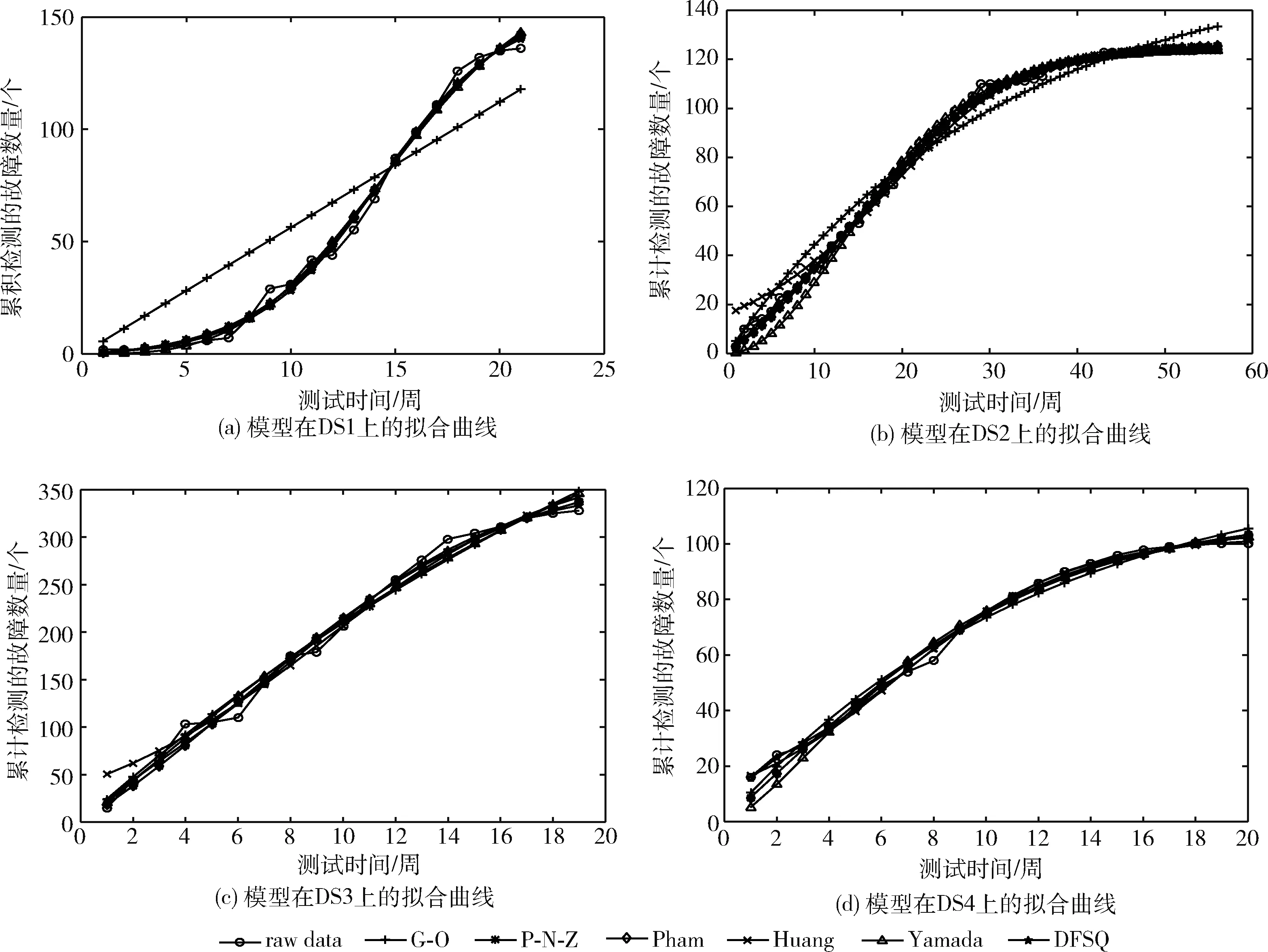
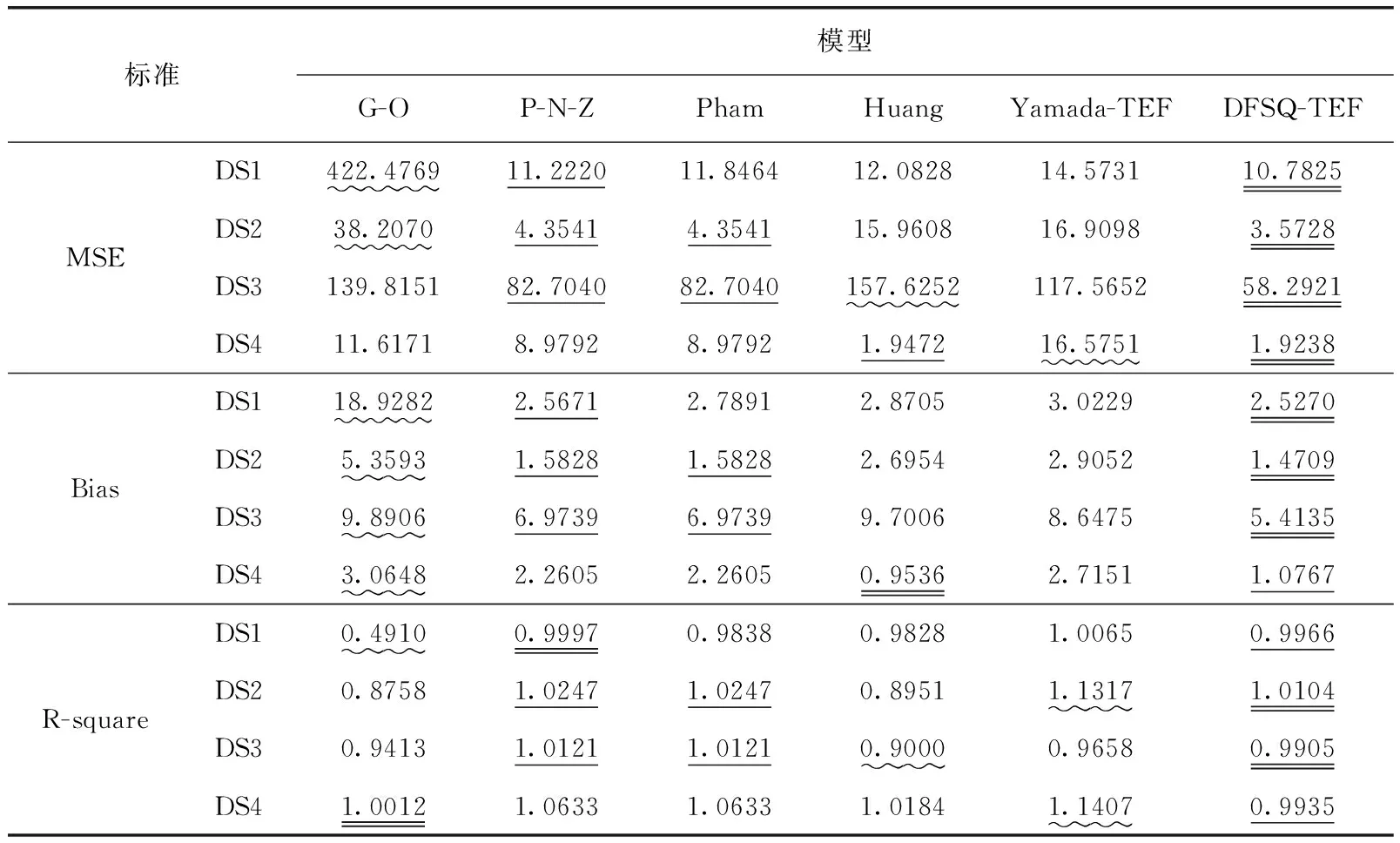
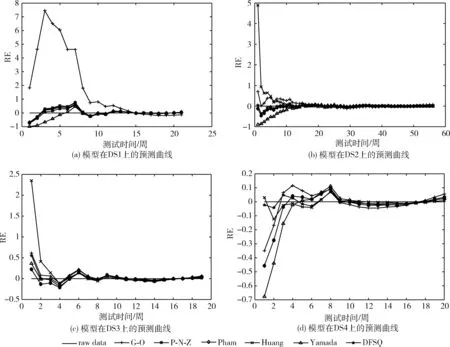
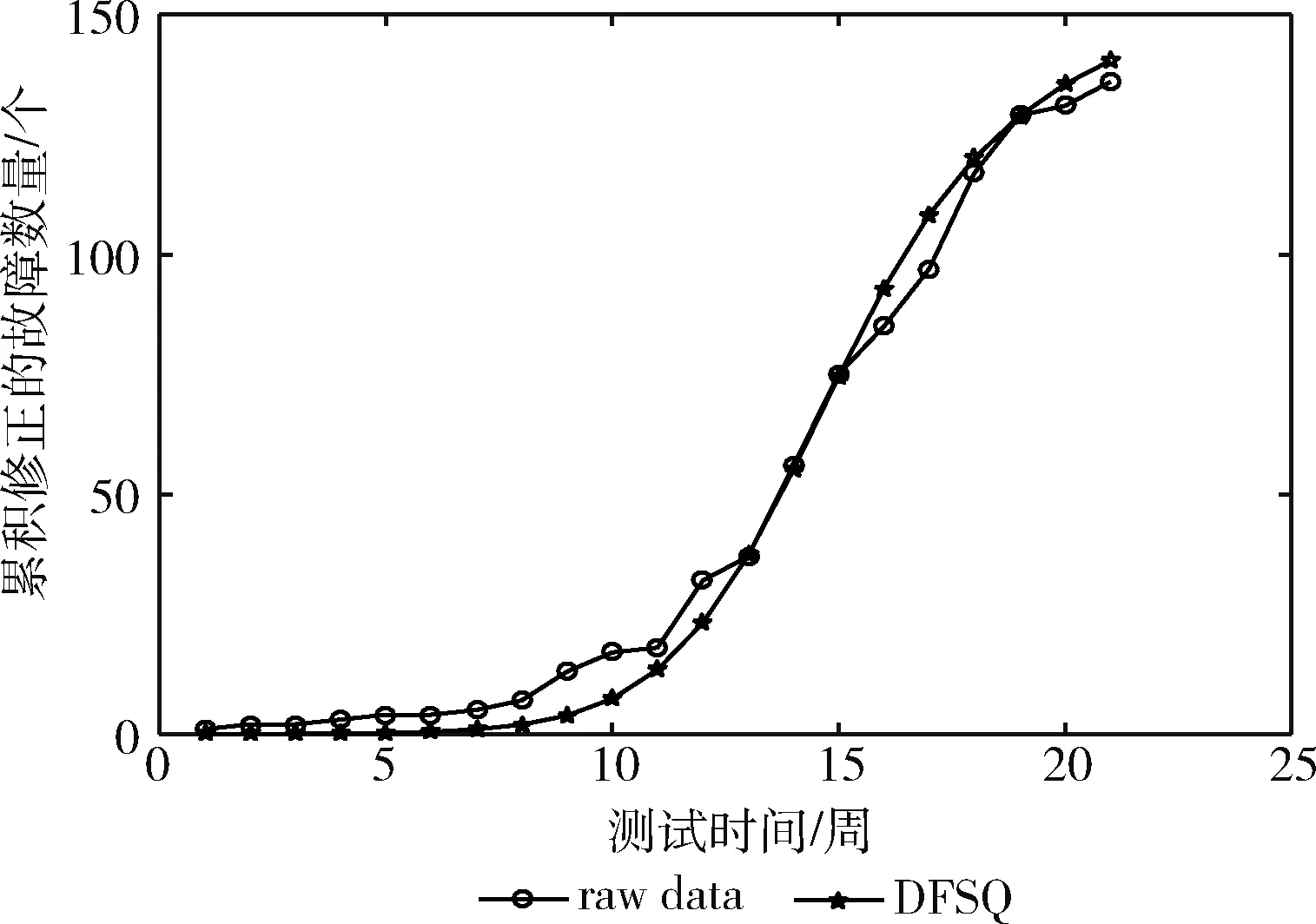
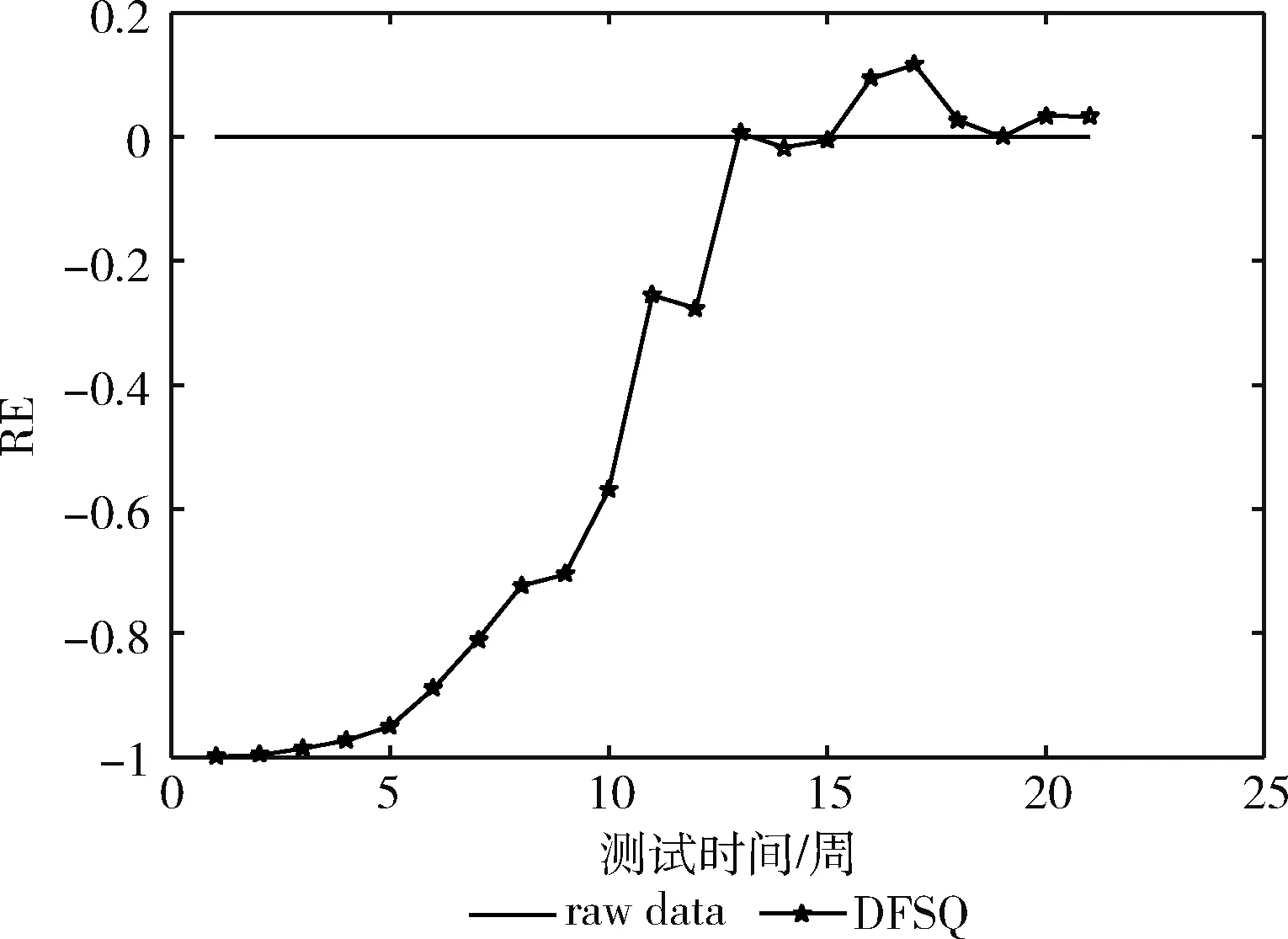
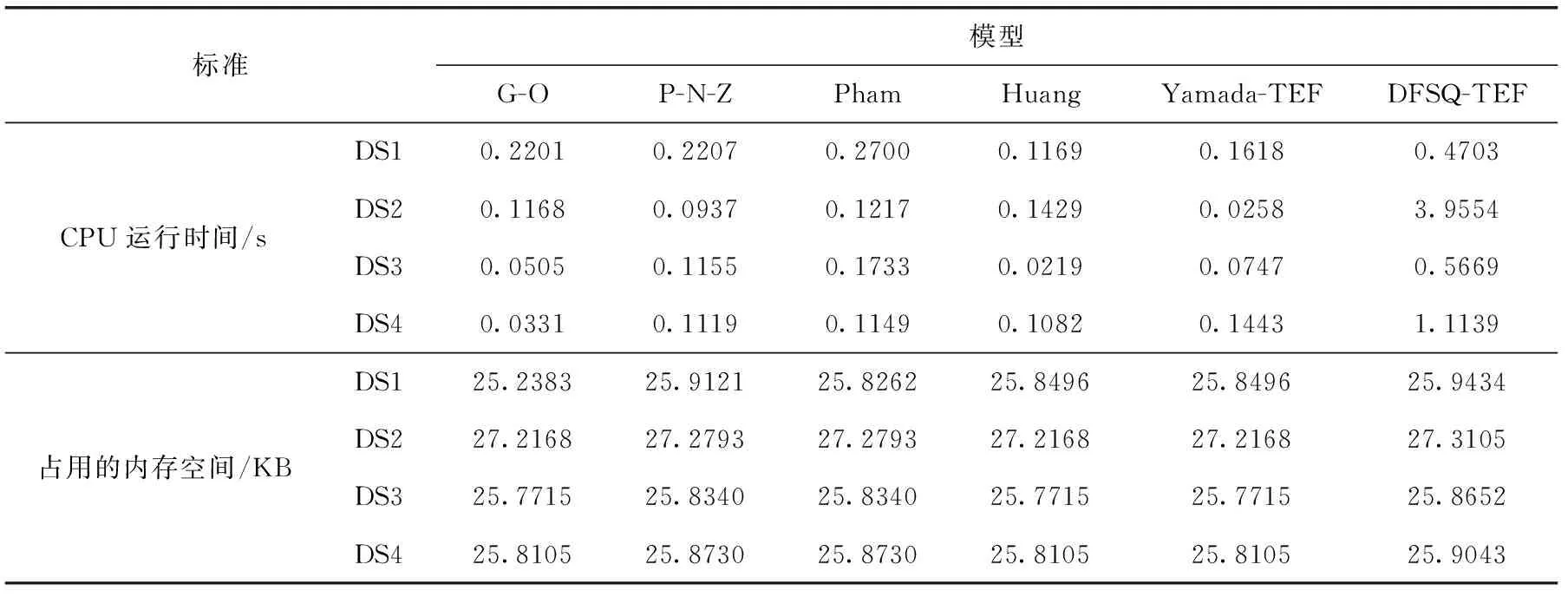
由于失效數據集通常數據量較小,因此本文采用最小二乘法擬合模型參數,以故障檢測過程模型為例:設數據集中一共采集到n組故障數據信息,在時間區間(0,ti)內,實際檢測出的累積故障數量為mi,模型預估出的累積故障數量的均值函數為md(ti), 其中i=1,2,…,n; 0 接下來只需對SSR中未知的參數逐個求偏導,并令求導后的結果等于0,即可求出使得SSR達到極小化的參數估計值。本文采用分步方法,首先基于測試工作量數據,擬合出Wd(t)中的參數估計值,見表2,然后將估計出的參數值代入模型中對md(t)中剩余的參數進行計算,估計結果見表3。 表2 測試工作量函數的參數估計值 表3 參與比較的模型的參數估計值 3.4.1 故障檢測過程 檢測過程的擬合曲線如圖3所示,從中可以觀察到,在DS1和DS2上,G-O模型的擬合曲線嚴重偏離實測數據的失效曲線,主要原因在于G-O模型的建立沒有充分考慮真實情況,假設條件過于簡化;Huang模型和Yamada模型在建模過程中本質相同,但可以明顯看到Huang模型在測試周期開始時擬合效果不佳,幾個周期過后表現得較好,兩個模型表現出的性能各異,原因在于模型之間采用的TEF存在很大的差異。新建模型在所有4個失效數據集上,性能表現穩定,與真實失效曲線擬合程度較高,體現出良好的擬合能力。 圖3 各個模型的累積檢測的故障數量擬合曲線 為進一步比較不同模型的性能差異,下面定量化地計算出各個模型在3個判定標準上的數值,具體數據見表4,其中帶有雙下劃線標注的表示最優標準值,帶有下劃線的表示次優標準值,最差標準值采用波浪線表示。 表4 模型的擬合性能度量比較 從表4可以看出,在DS1上,新建模型表現最優,在3個比較標準中,2個最優,1個次優,且與最優的標準值僅相差在小數點后第三位上;P-N-Z模型次之,1個最優,2個次優;G-O模型表現最差,3個標準均是最差。在DS2上,新建模型表現最優,在3個比較標準中均是最優;P-N-Z和Pham模型次之,3個均是次優;G-O模型表現最差,3個標準均是最差。在DS3上,新建模型表現最優,在3個比較標準中均是最優;P-N-Z模型和Pham模型性能表現相同,優于剩下的模型,3個標準值均是次優;Huang模型表現不理想,MSE和S-square標準均是最差,而Bias接近最差。在DS4上,新建模型表現依舊穩定,在3個比較標準中,1個最優,2個次優,且與最優的標準值相差不大;Huang模型次之,1個最優,1個次優;Yamada模型表現不理想,MSE和R-square標準均是最差,而Bias接近最差。新建模型性能表現良好,可能基于以下原因: (1)新建模型在建模過程中考慮到FDR的復雜性,與TEF相結合構建出復合型FDR,實現了對故障檢測過程更為真實的描述; (2)考慮到引入測試工作量因素,且選取了變形S型TEF,更準確地反映了測試過程中測試工作量的變化情況; (3)應用不完美排錯對故障修正過程引入新故障的現象進行建模,充分體現程序結構的關聯性以及環境和人員的隨機性; (4)排隊論的引入進一步挖掘了故障所經過的活動歷程,基于隊列的研究,時間延遲這一必不可少的環節得以進行模型化表示。 另一方面,檢測過程的預測曲線如圖4所示,從中可以觀察到,G-O模型在DS1上預測效果很不理想,但在另外3個數據集上呈現出的效果明顯好于DS1,說明模型適用性差,具有極強的不穩定性;Huang模型的RE值在DS2、DS3和DS4上第一周期偏離0異常明顯,但是從第二周期開始迅速趨近于0,并且預測效果越來越好;新建模型在4個數據集上的預測效果表現優異,波動范圍較小,可以清晰地看到優于其它模型;所有模型的RE圖有一個共同特點,后期預測性能均優于前期,尤其是在12周之后。這是因為利用SRGM進行可靠性預測,首先需要充足的數據作為支撐;同時由于模型中的參數數量不一,需要數據規模超過參數數目一定的比例,才能達到更好的預測性能。 圖4 各個模型的預測RE曲線 3.4.2 故障修正過程 失效數據集根據采集到的故障屬性列一般可分為兩種類型[12]:一種是只包含累積檢測的故障數量屬性,目前這種數據集在數量上占據著很大的優勢,但對于其應用的局限性正在逐漸顯露出來;另一種是除累積檢測到的故障數量外同時包含累積修正的故障數量屬性,全面的故障屬性列更符合當前的研究趨勢。DS1屬于第二種數據類型,而DS2、DS3以及DS4均屬于第一種,故接下來只使用DS1對故障修正過程的模型進行驗證。前5個經典模型在建模過程中并沒有將故障檢測過程與故障修正過程作為兩個不同的階段進行考慮,因此5個經典模型無法對DS1中故障修正過程進行建模。本文只對新建模型的故障修正階段性能進行分析,并與模型的檢測階段性能進行縱向對比,其中修正階段模型的參數估計值見表5。 表5 提出模型的參數估計值 修正過程的擬合曲線如圖5所示,從中可以看出,新建模型在故障修正過程中與真實數據的失效曲線貼合緊密,展現出較好的擬合能力,進一步,通過表6中的擬合標準,可以更直觀地判斷模型的性能。與故障檢測過程相比,模型的擬合標準值有一定的下降,但下降的幅度并沒有超過標準自身的量級,仍然展現出比較好的擬合效果。原因在于故障修正過程的建模是以故障檢測過程為基礎,會使用檢測過程中估計出的參數值,這些參數值本身與實際情況存在誤差,代入修正過程后導致最終結果的誤差進一步擴大。 圖5 提出模型在DS1上的擬合曲線 表6 提出模型的擬合性能度量 另一方面,修正過程的預測曲線如圖6所示,從中可以看出,模型故障修正過程的預測曲線與檢測過程呈現相同的變化趨勢,后期預測性能明顯優于前期,雖然沒有故障檢測過程的預測能力表現優異,但RE值的最大變化范圍沒有超過1,還是展現出比較好的預測能力。 圖6 提出模型在DS1上的預測曲線 3.4.3 模型復雜度分析 新建模型由于結構復雜以及參數量增多導致模型的復雜度有顯著提高,通過統計相同硬件條件下各個模型執行1000次所用的平均CPU運行時間以及參數和變量占用的內存空間,對模型的計算性能進行分析。具體數據見表7。 表7 模型的計算性能度量比較 由表7可知新建模型的CPU運行時間相比于其它模型有數倍到數十倍的增加,在數據規模較大的DS2上表現尤為明顯,隨著輸入數據量的增大,模型的運行時間差距會進一步擴大。但由于失效數據集的規模通常較小,模型的CPU運行時間保持在零點幾秒到幾秒之間,相比于模型擬合和預測精度的提升,所付出的時間代價是可接受的。同時各個模型中參數和變量占用的內存空間在幾十KB范圍,所有模型處于同一個數量級,且差異很小,不會對當前的計算機硬件環境形成挑戰。因此,新建模型雖然復雜度有顯著提升,但在解決軟件可靠性評估和預測的問題上是可行的,并且結果是更精確的。 本文建立的基于雙排隊系統的SRGM,考慮到故障檢測過程和故障修正過程中存在的時間延遲現象,并基于測試工作量函數對故障檢測率進行重構,實現了對真實測試過程更為符合現實的描述。通過對比實驗驗證在選定的失效數據集上與若干經典SRGM相比,其展現出更好的預測效果和擬合能力。新建立的模型存在的問題便是引入了更多的參數,導致模型的復雜度上升和可理解性下降。未來,通過對排隊論技術的進一步研究,向著模型復雜度更低,性能更優的方向發展。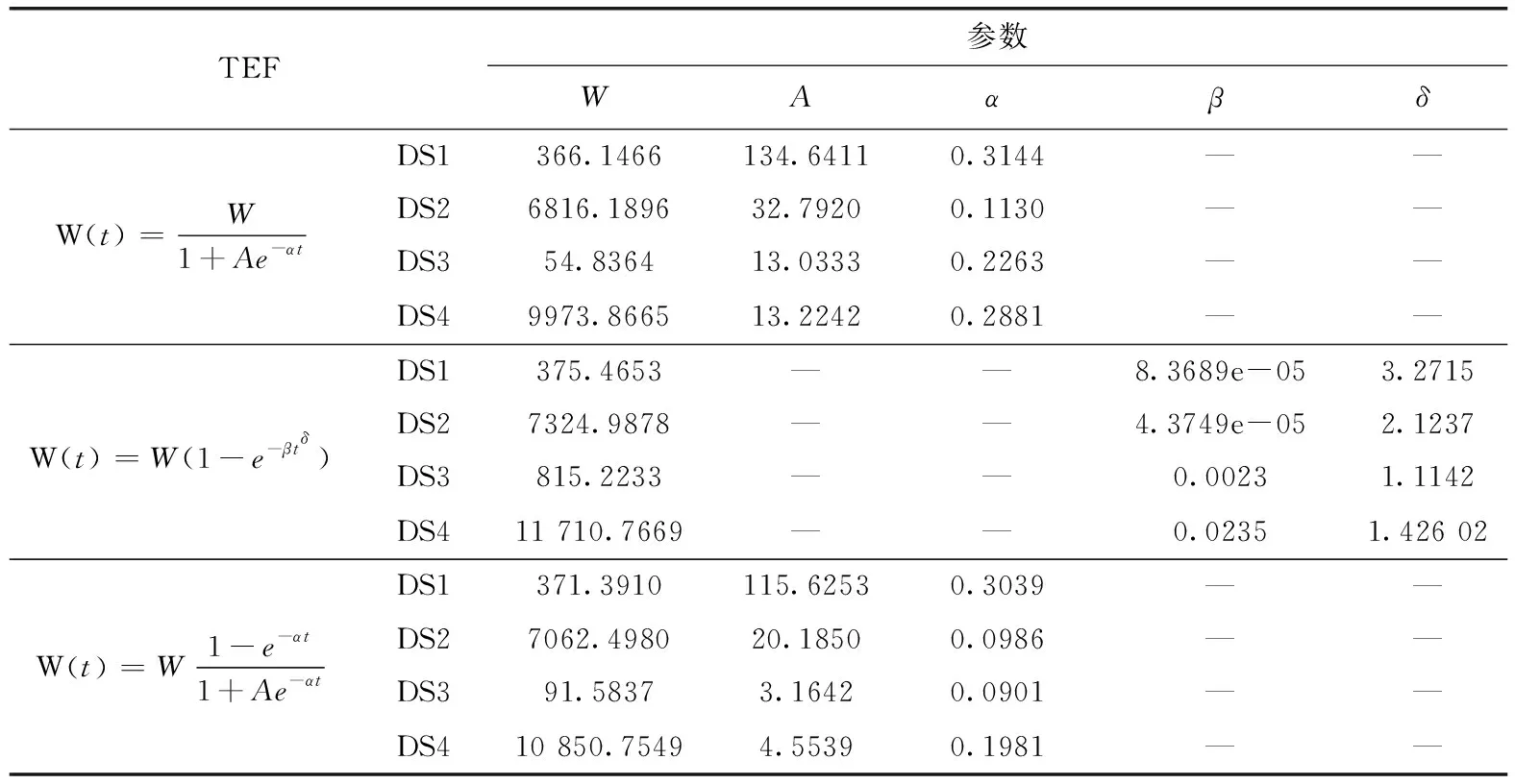

3.4 模型性能的比較分析

4 結束語

