循環穩態或單調態下薄片小試樣應力-應變關系試驗方法

張澤權，蔡力勛，黃茂波，韓光照

(西南交通大學 力學與航空航天學院 應用力學與結構安全四川省重點實驗室，四川 成都 610031)

在航空航天、石油化工、核電等領域，結構部件在單向或循環載荷作用下會產生局部永久性損傷而失效，研究材料單調態或循環穩態下的力學性能可為結構的安全評價與抗疲勞設計提供基礎依據[1-3]，在工程應用中，不可避免地需要精確評估在役部件的材料力學性能、剩余壽命，因材料尺寸和服役結構材料取樣的限制及結構小型化設計趨勢，試樣尺寸為厘米、分米級的標準圓棒試樣[4-5]難以滿足材料力學性能試驗要求，基于這些需求，小試樣測試技術變得備受關注。

國內外學者對小試樣測試材料的力學性能進行了一些探索。小試樣試驗的通常方法是將傳統試樣的幾何尺寸進行等比例縮小，Lucas[6]對堆芯材料和壓力容器輻照試驗中采用的不同幾何形狀小試樣和測試技術進行了描述，Kumar等[7]通過實驗來確定微型拉伸試樣標準截面中的最小材料體積，以獲得與標準試樣的力學性能數據相當的力學性能數據，Liu等[8]考慮到輻照設備的體積限制和對試樣放射性的嚴格限制，提出了一種經優化的“狗骨型”小型平板拉伸試樣，通過該試樣獲取核反應堆材料的單調應力-應變關系。循環應力幅-應變幅曲線可反映循環變形下材料變形抗力的重要特性，Skelton等[9]的研究表明，將在不同應變幅下獲得的滯回曲線最低點都移到0點位置，如果這些相對滯回曲線是相互重合的，則該材料表現出Masing特性。對于符合Masing效應的材料，Read等[10-11]通過設計啞鈴狀薄片試樣完成拉-拉載荷控制下的循環試驗，獲得了電子束蒸發銅的力學性能，但并未進行拉壓載荷控制獲得穩態循環下材料的單軸應力-應變關系(簡稱循環本構關系)。Melander等[12-14]通過設計厚度為1.4 mm、長寬比小于2的等直板狀試樣完成了變幅應變控制下的拉壓循環試驗，但最大應變幅超過0.25%時會發生失穩，Martin[15]和Wisner等[16]提出了沙漏半徑等于沙漏根部寬度的一種用于對稱應變循環加載的薄片沙漏試樣，發現軸向應變幅不超過1.5%時，所有試樣均未發生失穩，但Martin等分別采用沙漏根部橫截面的平均應變幅和平均應力幅作為軸向應變幅和軸向應力幅，與沙漏根部處于單向應力狀態的材料代表性體積單元(RVE)的真實應變幅、應力幅存在較大偏差。黃學偉等[17]根據有限元分析(FEA)，建立了Zr-Sn-Nb合金薄片沙漏試樣側跨位移(名義應變)與沙漏根部軸向應變之間的轉換方程。由于黃學偉等采用的是單調單軸應力-應變關系完成FEA，未考慮低周疲勞過程中材料的循環軟化或硬化。賈琦等[18-19]采用標準圓棒試樣的循環本構關系對薄片沙漏試樣進行FEA，該方法未解決基于薄片試樣直接獲取材料循環應力幅-應變幅關系的問題[20]，尹濤等[21]完成了毫米厚度的薄片沙漏試樣的低周疲勞試驗設計，通過建立能量分離函數較準確地預測了材料的循環應力幅-應變幅關系，而這種能量分離的方式缺乏理論性。劉勤等[22-24]針對Martin型試樣，建立了描述材料循環本構關系參數、試樣幾何尺寸、側跨位移幅和載荷幅之間關系的理論方程，該理論方程對薄片沙漏試樣幾何尺寸的表征相對復雜，并未建立側跨位移幅、載荷幅與循環等效應力幅、等效應變幅的直接聯系，其理論方程的簡捷性及應變幅、應力幅的回歸式轉換公式的材料與幾何普適性均有不足。

本文基于能量密度等效[25-27]，針對材料各向同性、應力-應變關系符合Ramberg-Osgood律(R-O律)的薄片沙漏試樣，提出RVE彈塑性變形位移-載荷關系理論方程和等效應力、等效應變理論方程，進而提出金屬薄片沙漏試樣循環穩態或單調態的等效應力-等效應變關系試驗方法。

1 材料彈塑性理論方程

1.1 位移-載荷關系理論方程

針對材料均勻、連續和各向同性的單向受載構元，根據能量密度等效方法，構元的變形能可表示為能量密度等效點(簡稱M點)的應變能密度和有效變形域體積的乘積[25]，即：

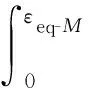
(1)

式中：U為構元試樣的總變形能；Veff為有效變形域體積；σeq-M和εeq-M分別為M單元的等效應力和等效應變。

假定材料應力σ和應變ε的關系符合R-O律，則等效應力σeq、等效應變εeq間的關系[28]可表示為：

(2)

式中：εe-eq和εp-eq分別為RVE的等效彈性應變和等效塑性應變；E、K和N分別為彈性模量、應變強化系數和應力硬化指數。

(3)

(4)

在準靜態加載條件下，根據功能原理，外力功W與軸向載荷P作用下的試樣變形能U相等，即W=U，則：

(5)

將式(4)代入式(5)，等式兩端分別對he和hp求導，并作無量綱化整理可得：

(6)

(7)

假定純彈性條件下加載線位移he與側跨位移he-s、純塑性條件下加載線位移hp與側跨位移hp-s滿足比例關系：

(8)

式中，a1和a2均為比例系數。

根據文獻[20]中彈塑性荷載-位移關系的工程估計方法，彈塑性條件下的側跨位移hs可由he-s和hp-s進行工程疊加，即：

hs=he-s+hp-s

(9)

由式(7)～(9)整理可得：

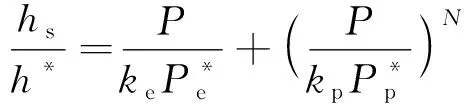
(10)

(11)

(12)

式中，ke和kp分別為純彈性和純塑性條件下的無量綱側跨位移-載荷系數。易發現，式(6)和(7)中的半理論方程也可用于研究側跨位移與載荷的關系，其參數he、hp、k0、k1、k2由he-s、hp-s、ke、kp1、kp2代替，式(6)、(7)和式(10)～(12)分別稱為加載線和側跨位移-載荷關系理論方程。

1.2 等效應力、等效應變理論方程

根據量綱分析方法，假設在純塑性條件下M點RVE的等效應力σeq-M與載荷P、加載線位移hp滿足如下關系：

(13)

式中，k3和m均為純等效塑性應力常數。

將式(13)和式(3)、(4)代入式(1)，可得在純塑性變形條件下，構元有效變形域內總變形能Up：

(14)

在準靜態加載條件下，根據功能原理W=U，則：

(15)

將式(6)、(7)代入式(15)，等式兩端分別對純塑性位移hp積分，整理可得：

(16)

考慮等式右側為常數，則等式左側無量綱塑性位移hp/h*的指數必然為0，即m=0，等式左側項為系數1，進而k3、m可表示為：

(17)

則純塑性條件下M點RVE的等效應力、等效應變可表示為：

(18)

由式(9)～(12)整理可得he-s、hp-s的計算公式：

(19)

由式(2)、(18)和(19)整理可得：

(20)

式(20)稱為彈塑性條件下以側跨位移、載荷表征M點RVE的等效應力、等效應變理論方程。

在穩態應變循環下，針對符合Masing效應的金屬材料，循環穩定應力幅σa-應變幅εa關系可作為循環穩定時的材料單軸應力-應變關系。針對不符合Masing效應的金屬材料，也可采用循環穩定的σa-εa關系近似表達，以載荷幅Pa、純彈性側跨位移幅he-as、純塑性側跨位移幅hp-as、循環等效應力幅σeq-M-a和循環等效應變幅εeq-M-a分別替代式(20)中的P、he-s、hp-s、σeq-M和εeq-M，可得彈塑性條件下以側跨位移幅、載荷幅表征M點RVE的循環等效應力幅、等效應變幅理論方程。

1.3 循環穩態或單調態的等效應力-等效應變關系試驗方法

基于等效應力、等效應變理論方程，提出金屬薄片沙漏試樣循環穩態或單調態的等效應力-等效應變關系試驗方法。以不同應變幅對稱應變循環試驗為例，可通過側跨位移幅、載荷幅直接獲取材料循環穩定的應力幅-應變幅關系。具體方法如下：通過數據采集和處理可獲得試樣每級控制應變幅下循環穩定的側跨位移-載荷滯回環，并獲取各級應變幅對應的載荷幅與側跨位移幅數據(Pa，has)，以Pa-has曲線的線性段斜率確定參量η，進而由式(19)獲得彈性模量E與純塑性側跨位移幅hp-as；然后可由式(18)得到純塑性條件下的循環等效應力幅-應變幅關系，進而得到R-O律中的循環應變強化系數Ka和循環應力硬化指數Na；最后基于循環等效應力幅、等效應變幅理論方程，可獲取M點RVE的數據(σeq-M-a，εeq-M-a)，即材料循環穩定時的等效應力幅-等效應變幅關系。

2 方程參數確定方法

2.1 有限元分析模型

沙漏試樣幾何構型如圖1所示，試樣長度為H，厚度為t，試樣的夾持端寬度為w，沙漏半徑為R，應變引伸計安裝在C-D處進行側跨沙漏位移(名義應變)控制。采用ANSYS14.5商用FEA軟件模擬薄片沙漏試樣的彈塑性變形行為，圖2為薄片沙漏試樣的FEA網格模型，采用Plane183單元和平面應力條件，試樣一端施加固定約束，另一端施加位移，分別將試樣跨沙漏兩側C、D兩節點之間位移的變化量作為側跨位移hs、位移加載端所有節點的載荷之和作為載荷P進行研究。

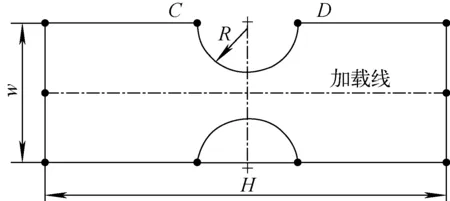
圖1 沙漏試樣幾何構型Fig.1 Geometric configuration diagram of hourglass specimen

圖2 沙漏試樣FEA網格模型Fig.2 FEA mesh model of hourglass specimen

2.2 參數確定方法

位移-載荷關系理論方程(式(10)～(12))是描述薄片沙漏試樣的幾何尺寸(w，R)、R-O律參數(E，K，N)、側跨位移和載荷之間關系的半解析方程，在無量綱的表達上該方程應具有材料和幾何普適性。方程含有的5個未知參量me、mp、ke、kp1和kp2，可采用1種E和K、5種N本構關系的5種特定材料FEA確定。

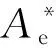
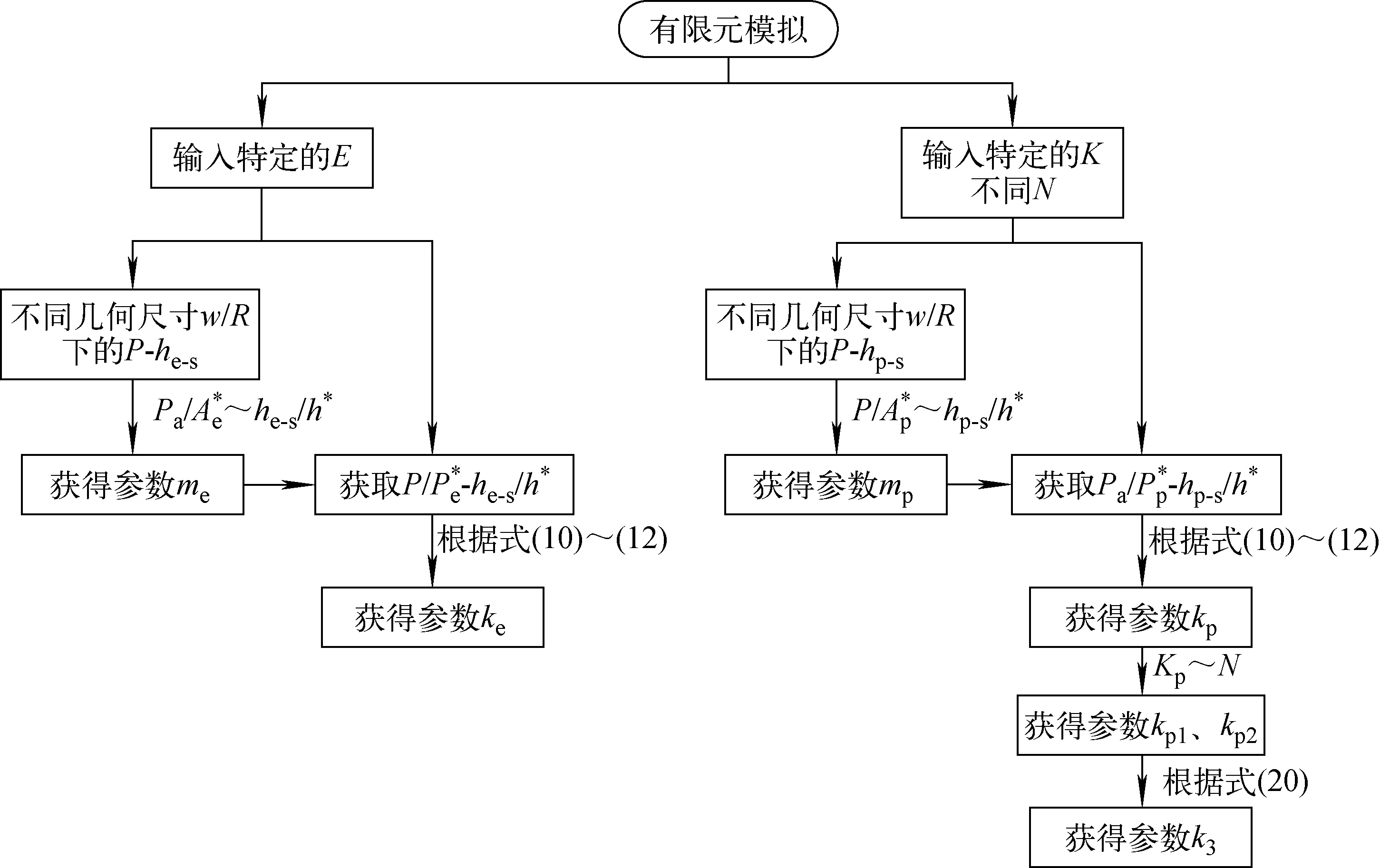
圖3 方程參數確定方法Fig.3 Determination method of equation parameter

表1 方程參數值及應用范圍Table 1 Parameter value and application range of equation

3 有限元驗證

將R-O律應力-應變關系作為條件本構關系進行有限元數值模擬，通過有限元分析得到位移-載荷數據組{P，hs}，采用理論方程可直接預測得到材料的本構關系曲線。

對于幾何尺寸為w=15 mm、R=5 mm的薄片沙漏試樣，材料常數分別取為E={80 GPa，210 GPa}、K={400 MPa，700 MPa，1 000 MPa，1 300 MPa}和N={4，6，8，10，12}；對于等比例幾何尺寸為w=9 mm、R=3 mm與非等比例幾何尺寸w/R分別為3.00、3.25、3.50、3.75的薄片沙漏試樣，材料常數分別取為E={80 GPa，210 GPa}、K=1 000 MPa、N=10。通過理論方程獲得的預測曲線與FEA的條件R-O律曲線示于圖4。結果表明，R-O律預測曲線與FEA條件曲線均密切吻合。可見，等效應力、等效應變理論方程能較準確地反映不同材料、不同幾何尺寸的σa-εa關系。

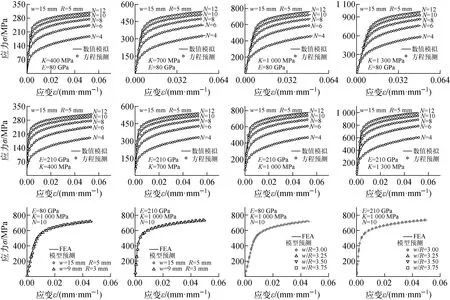
圖4 等效應力、等效應變理論方程驗證Fig.4 Verification of equivalent stress and equivalent strain theoretical equations

4 試驗方法應用

由金屬薄片沙漏試樣循環穩態或單調態的等效應力-等效應變關系試驗方法可直接得到材料的單調拉伸應力-應變關系或穩態對稱循環下應力-應變關系。為證實該方法的有效性，與標準圓棒試樣拉伸和不同應變幅對稱應變循環試驗結果進行比對。

4.1 試驗條件

為驗證金屬材料在循環穩態或單調態下的應力-應變關系的唯一性，本文設計用于拉伸和不同應變幅下的對稱應變循環試驗的薄片沙漏試樣有微小尺寸和小尺寸兩種幾何尺寸，微小尺寸H、w、R、t分別為10、3.6、1.25、0.7 mm，小尺寸H、w、R、t分別為80、15、5、1 mm。薄片沙漏微小試樣在Care IBTC-300原位雙向拉壓疲勞試驗機上完成試驗(圖5a)，設備的載荷傳感器量程為1 kN。采用標距為5 mm、量程為-10%～30%的MTS632.29F-30應變引伸計進行側跨沙漏位移(名義應變)控制。薄片沙漏小試樣在美國MTS809 25kN電液伺服材料試驗機上完成試驗(圖5b)，其控制系統為FlexTest4.0，應用軟件為MPT；載荷傳感器和應變引伸計的型號分別為647.02B-22、MTS632.53F-14(標距l0為12 mm，軸向測量范圍為-10%～20%)，其精度均為0.5級，試驗機的靜載荷檢定滿足JJG 556—2011要求。

1——薄片沙漏微小試樣；2——薄片沙漏微小試樣加載裝置；3——Care試驗機左右夾頭；4——MTS 632.29F-30引伸計；5——MTS試驗機上下夾頭；6——薄片沙漏小試樣；7——薄片沙漏小試樣加載裝置；8——MTS 632.54F-14引伸計；9——標準圓棒試樣；10——MTS 632.03F-30 COD引伸計a——薄片沙漏微小試樣試驗裝置；b——薄片沙漏小試樣試驗裝置；c——標準圓棒試樣變幅對稱應變循環試驗裝置；d——標準圓棒試樣單軸拉伸試驗裝置圖5 試驗設備裝置圖Fig.5 Device diagram of test equipment

采用直徑為6 mm的標準圓棒試樣在美國MTS809 25kN電液伺服材料試驗機上完成的拉伸和不同應變幅下的對稱應變循環試驗(圖5c、d)作為對比試驗。

4.2 試驗材料

采用航空、核電領域的5種材料(分別是G115、16Mn、508-3steel、Cr12mov與P92)驗證該試驗方法對不同材料的普適性。5種材料的主要化學成分列于表2。

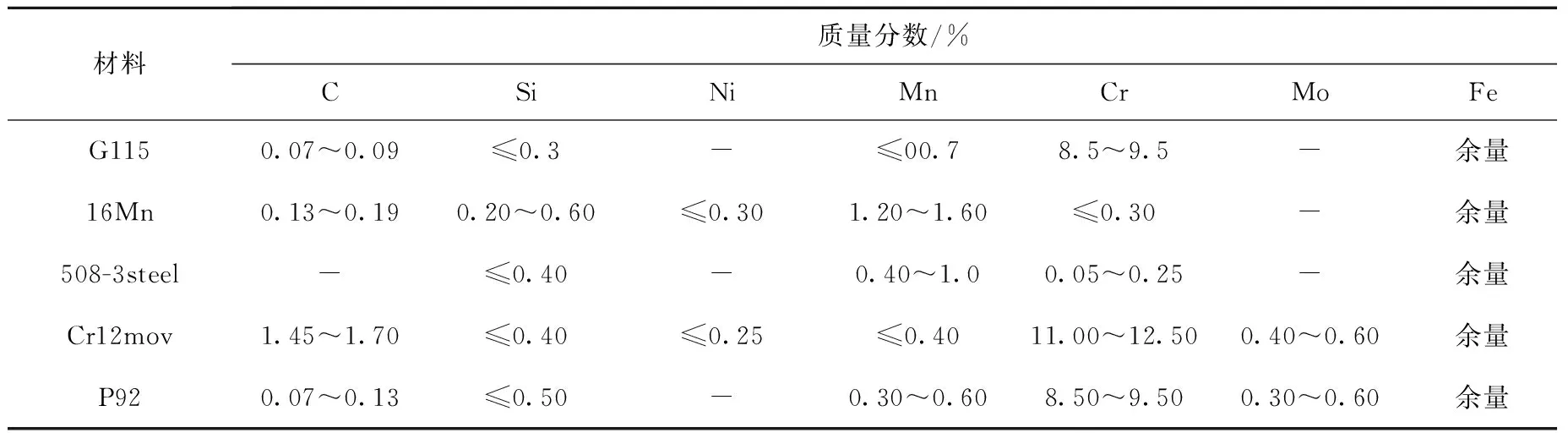
表2 材料化學成分Table 2 Chemical composition of material

4.3 材料單調應力-應變關系獲取

針對材料為G115和16Mn的薄片沙漏微小試樣和標準圓棒試樣，完成單軸拉伸試驗，分別測量跨沙漏試樣兩側位移，并獲取其位移-載荷曲線，如圖6所示。基于等效應力、等效應變理論方程可由試樣的位移-載荷曲線直接得到材料的單調本構關系曲線，如圖7所示。可看出，以微小試樣預測的σ-ε曲線與標準圓棒試樣單軸拉伸試驗結果吻合良好。

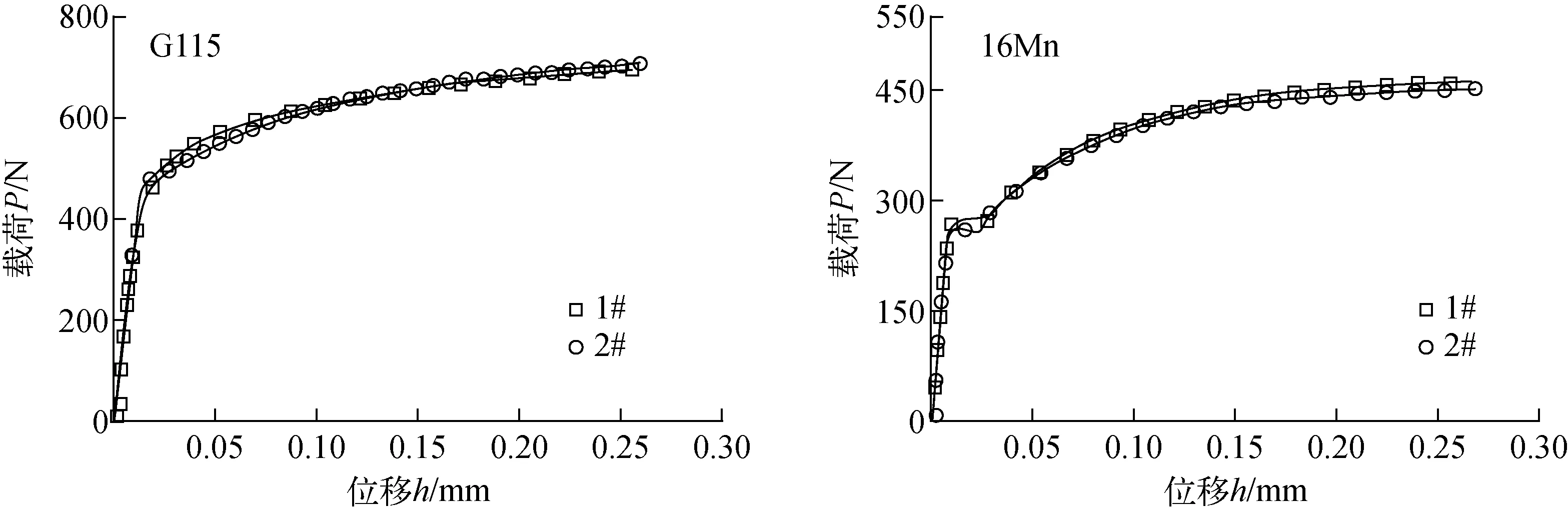
圖6 薄片沙漏微小試樣的載荷-位移曲線Fig.6 Load-displacement curve of thin hourglass small specimen

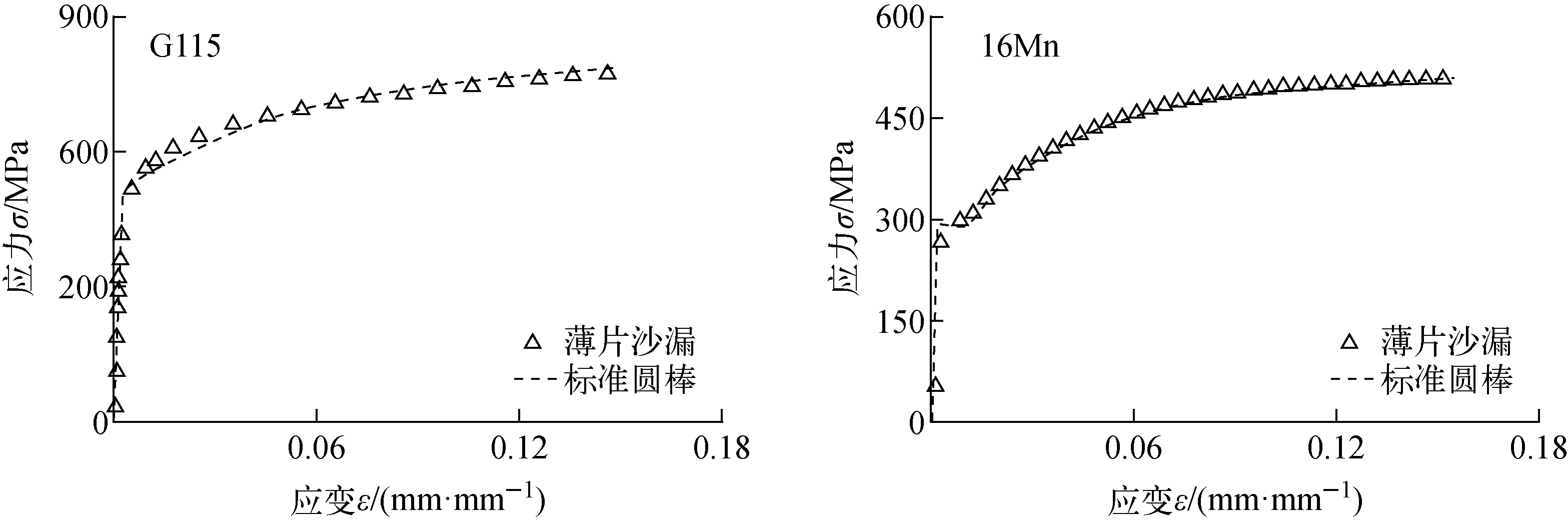
圖7 單軸拉伸σ-ε曲線Fig.7 σ-ε curve of uniaxial tension

4.4 材料循環應力幅-應變幅關系獲取

循環應力幅-應變幅關系曲線是材料疲勞性能的重要內容。金屬材料在等幅應變對稱循環的試驗過程中，隨著循環周次的增加，應力幅會逐漸增大或減小并趨于穩定，對應循環硬化或循環軟化。當位移幅使局部等效應力幅小于屈服強度時，應力幅-應變幅關系曲線表現為與單調拉伸應力-應變曲線彈性部分重合；當位移幅使局部等效應力幅超過屈服強度時，結構材料局部因產生循環塑性變形而表現出循環硬化或循環軟化現象，此時材料循環應力幅-應變幅曲線將高于或低于單調拉伸應力-應變關系曲線，且在循環載荷作用下的材料失效模式與單調拉伸狀態下存在明顯差異，如圖8所示。

圖8 失效模式對比Fig.8 Comparison of failure modes

針對材料為G115、16Mn、508-3steel、Cr12mov與P92的標準圓棒試樣，進行應變控制下的不同應變幅對稱循環加載可直接獲得循環穩定σ-ε滯回環(HL)，連接各級應變幅下的數據(σa，εa)得到σa-εa曲線，如圖9所示。

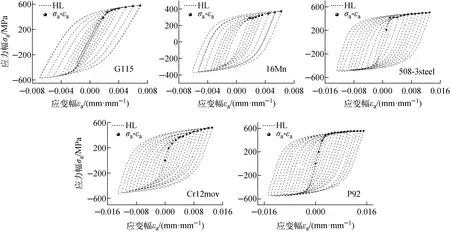
圖9 標準圓棒試樣循環穩定σa-εa曲線Fig.9 Cyclic stability σa-εa curve of standard circular bar specimens

針對材料為G115、16Mn的薄片沙漏微小試樣和材料為16Mn、508-3steel、Cr12mov、P92的薄片沙漏小試樣，獲取每級控制應變幅下循環穩定的側跨位移-載荷滯回環，其載荷幅Pa和位移幅has等于循環試驗的最大載荷Pmax和最大位移hmax，因此可將載荷-位移滯回環的頂點數據(Pmax，hmax)相連接以確定位移幅-載荷幅曲線，圖10、11分別為G115、16Mn、508-3steel、Cr12mov和P92的HL與Pa-has曲線。

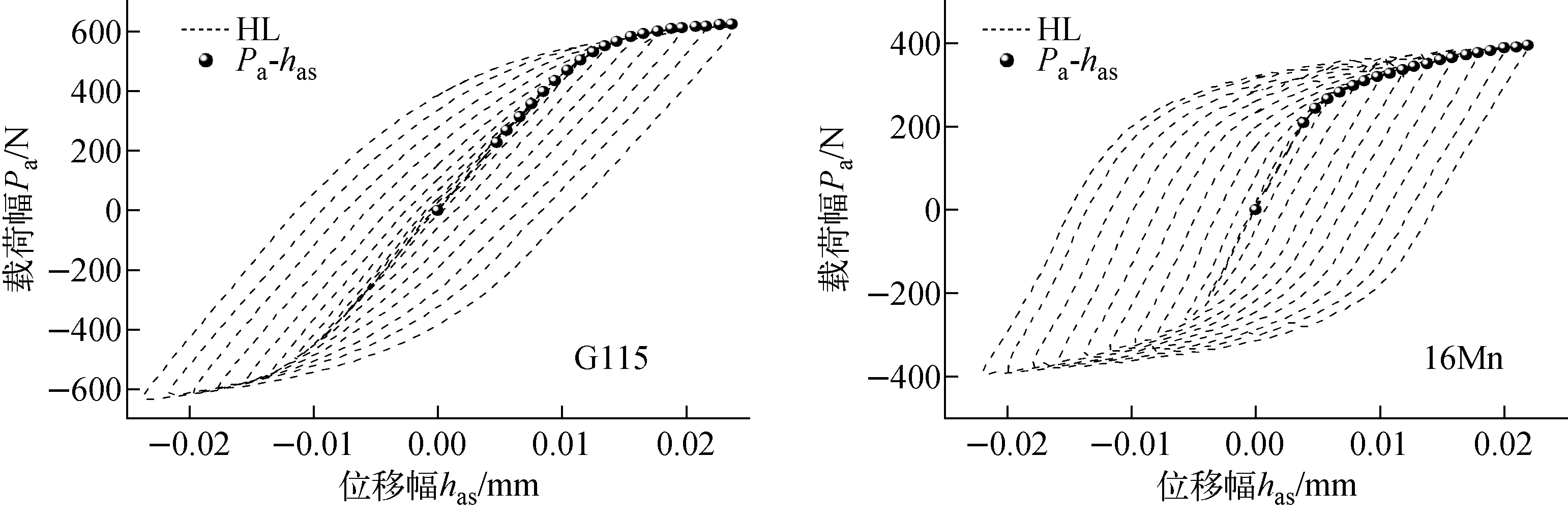
圖10 薄片沙漏微小試樣循環穩定HL與Pa-has曲線Fig.10 Cyclic stability HL and Pa-has curves of thin hourglass micro specimen

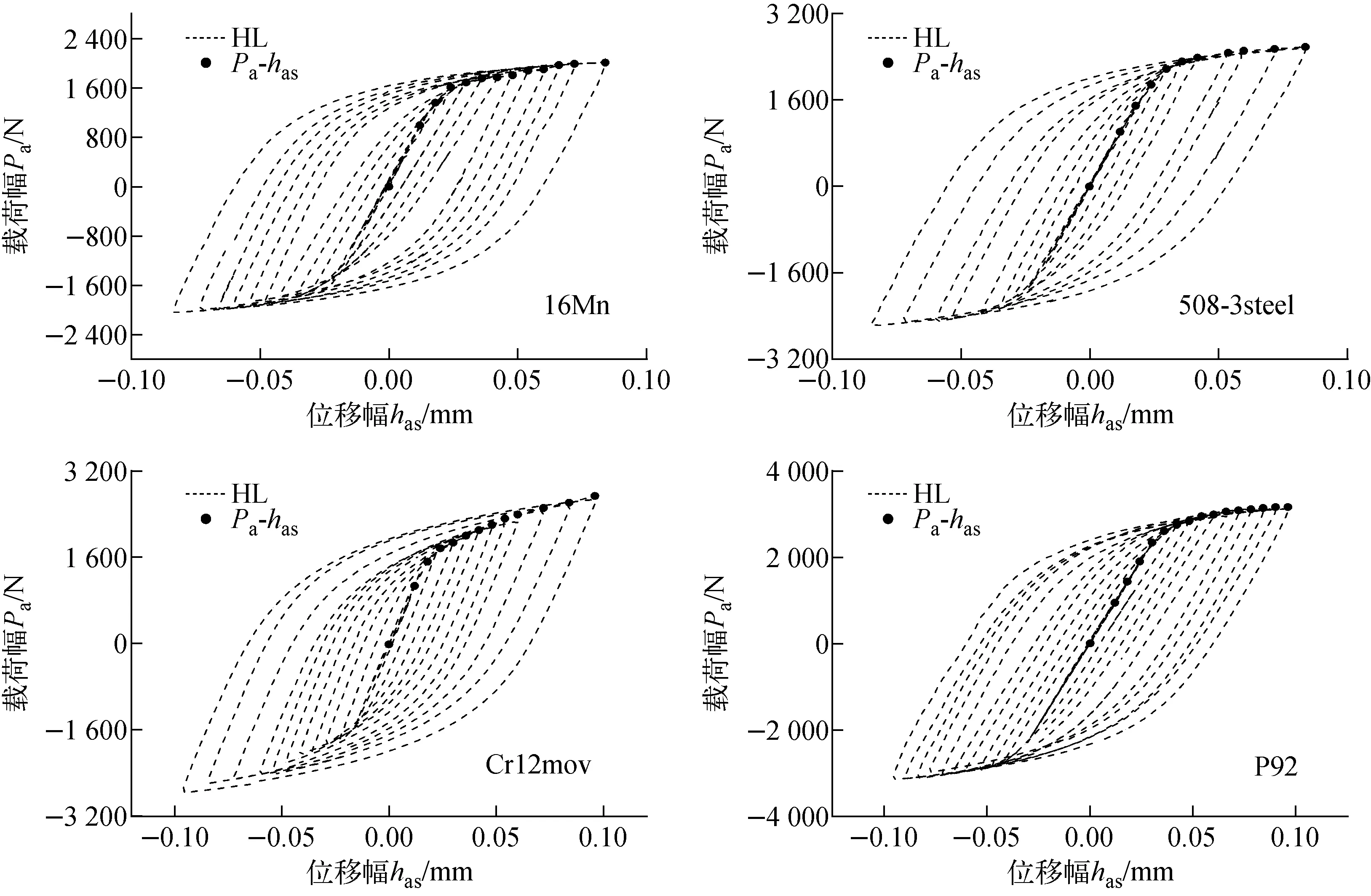
圖11 薄片沙漏小試樣循環穩定HL與Pa-has曲線Fig.11 Cyclic stability HL and Pa-has curves of thin hourglass small specimen

通過循環等效應力幅、等效應變幅理論方程由薄片沙漏試樣的Pa-has曲線直接得到σeq-M-a、εeq-M-a，圖12、13分別給出了5種材料的σeq-M-a-εeq-M-a曲線、標準圓棒試樣的單調σ-ε曲線和循環穩定σa-εa曲線，表3列出了利用該試驗方法得到的5種材料循環穩態或單調態下的R-O律參數(E、K、N、Ka、Na)。

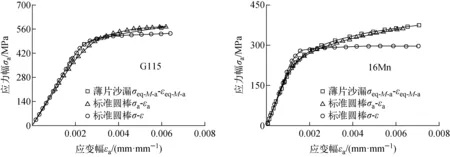
圖12 薄片沙漏微小試樣與標準圓棒試樣循環應力幅-應變幅曲線對比Fig.12 Comparison of cyclic stress amplitude-strain curvebetween thin hourglass micro specimen and standard round bar specimen

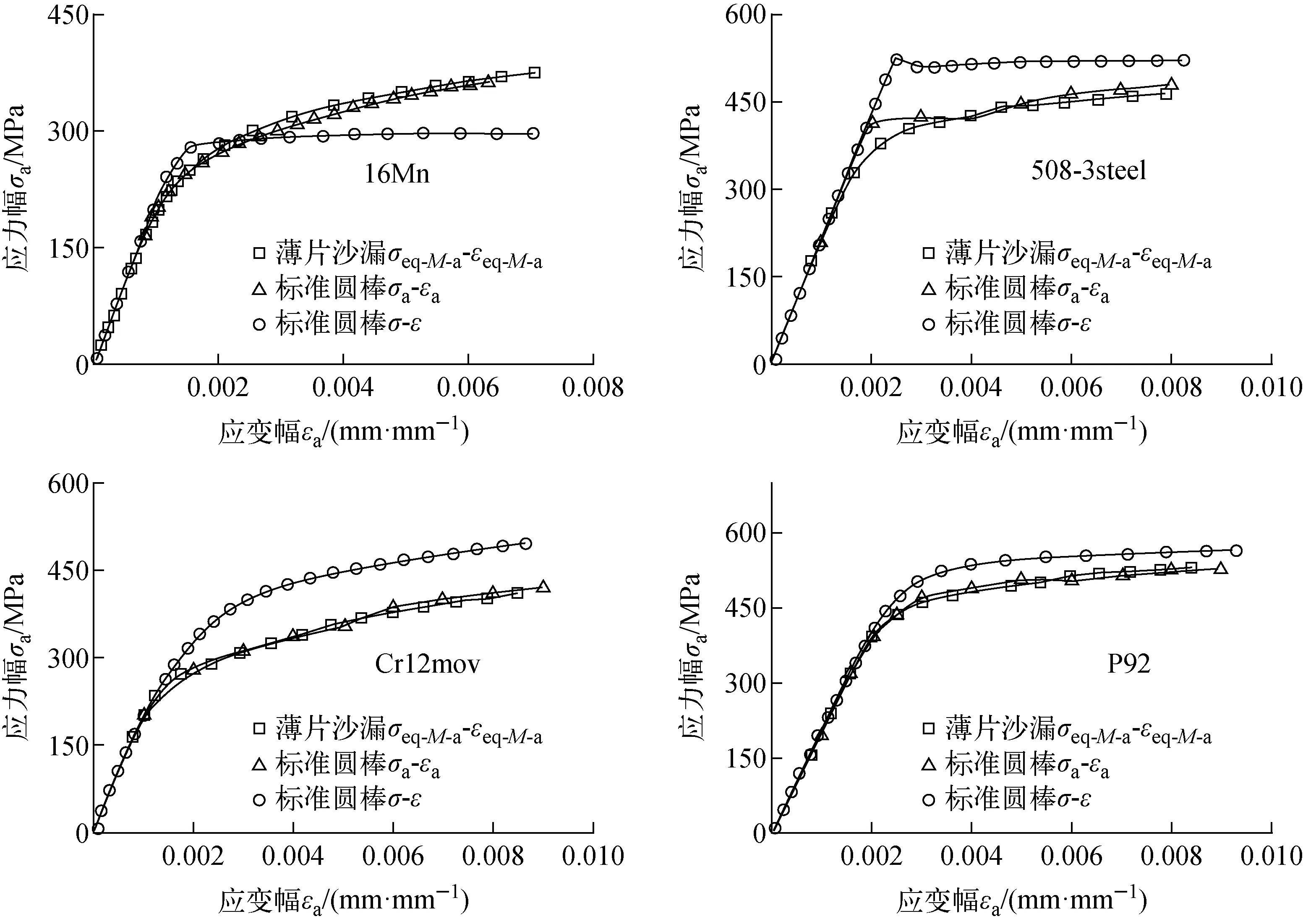
圖13 薄片沙漏小試樣與標準圓棒試樣循環應力幅-應變幅曲線對比Fig.13 Comparison of cyclic stress amplitude-strain curvebetween thin hourglass small specimen and standard round bar specimen

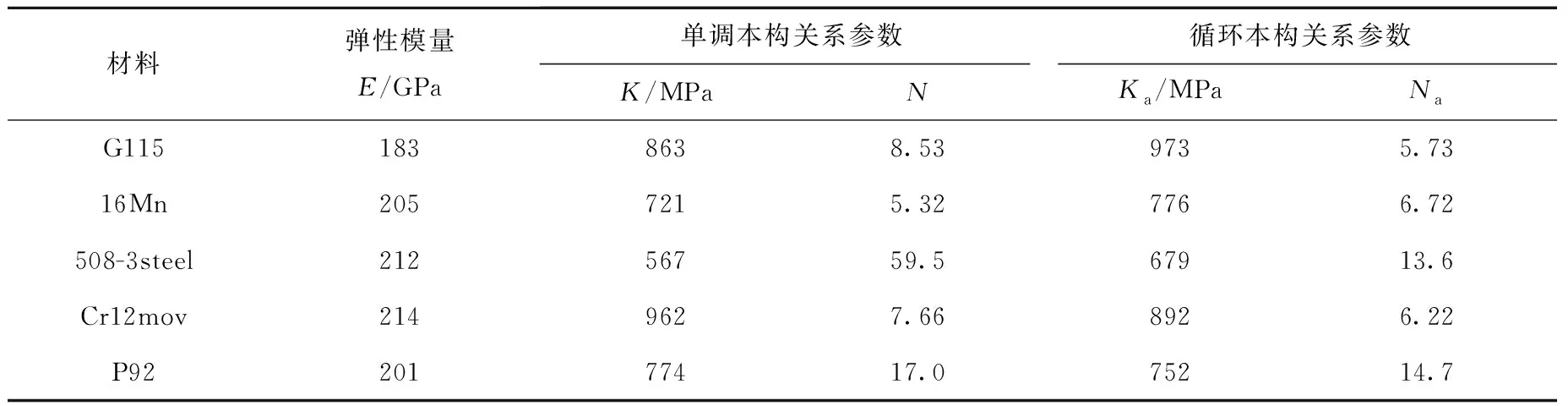
表3 單調及循環本構關系參數Table 3 Monotone and cyclic constitutive relation parameter

可看出，預測得到的應力幅-應變幅關系曲線與標準圓棒試樣的試驗曲線基本重合，說明在穩態應變循環下應力幅-應變幅關系是唯一的，與幾何構型無關。通過5種材料的單調應力-應變關系、循環應力幅-應變幅關系對比發現，G115和16Mn的σa-εa曲線高于σ-ε曲線，表現為循環硬化，Cr12mov、508-3steel和P92的σa-εa曲線均低于σ-ε曲線，表現為循環軟化。

5 結論

針對各向同性、本構關系符合R-O律的材料，本文基于能量密度等效，提出了金屬薄片沙漏試樣彈塑性理論方程與循環穩態或單調態的等效應力-等效應變關系試驗方法，得到如下結論：

1) 提出了薄片小試樣的彈塑性位移-載荷關系理論方程和等效應力、等效應變理論方程，并針對不同材料和幾何尺寸進行了FEA計算，由理論方程預測的薄片沙漏試樣等效應力-應變曲線與預設結果密切吻合；

2) 提出了金屬薄片沙漏試樣循環穩態或單調態的等效應力-等效應變關系試驗方法，針對5種合金材料、2種幾何尺寸的沙漏試樣，完成了單調拉伸和不同應變幅對稱應變循環試驗以及標準圓棒試樣拉伸和不同應變幅值對稱應變循環對比試驗，結果表明，該測試新方法與標準圓棒試樣的試驗方法所得單軸拉伸及單軸循環試驗結果基本一致。