基于粒子群算法的生鮮產品即時配送路徑優化

李 娜

（西安財經大學 管理學院，陜西 西安 710100）

1 問題描述及變量定義

1.1 問題描述

新零售背景下，多功能生鮮超市應運而生，人們越來越注重生鮮產品的新鮮度以及配送時間的長短，本文總結相關路徑優化研究現狀如下，張倩等[1]在研究配送路徑時，建立以配送成本，產品新鮮度，碳排放量為主的目標函數，并利用果蠅算法進行求解；肖建華[2]用變鄰域算法求解多車輛多配送中心的路徑優化問題；王超[3]設置軟時間窗約束研究即時配送的效果，并采用了布谷鳥進化算法求解PDVRP 問題。何美玲等[4]利用蟻群算法求解軟時間窗的路徑問題。姚臻等[5]以客戶時間窗、客戶滿意度、碳排放為約束條件，建立以碳排放量為基礎的總成本最小目標函數，并應用遺傳算法求解數學模型，得出考慮碳排放成本對于物流配送成本的重要影響。楊霞等[6]考慮生鮮產品新鮮度在軟時間窗約束的條件下對車輛路徑優化問題的影響，并用插點分段的方式計算兩需求點的距離，建立成本最小模型。秦馨等[7]根據當前訂單分批模式從訂單挑選搬運次數方面比較四種聚類算法的差別，最后得出相應結論。Fahimeh 等[8]針對訂單揀選和交付計劃這兩個重要且相互關聯的環節，從訂單批次揀貨處理以及向配送車輛分配訂單、規劃路線入手，以系統成本最小化為目標進行了充分研究，最終有效降低了系統成本并提高了揀選效率。Mar 等[9]也從訂單揀選和交付流程著手，對存在多個揀選配送位置的揀配問題進行研究，最終不僅減少了揀選和交付成本，還避免了閑置資源的浪費。實際生活中，訂單的產生是動態且具有規模性，需要考慮訂單分揀造成的時間差異對于消費者體驗度的影響，因此，考慮訂單分揀過程中造成的懲罰成本、新鮮度成本以及運輸過程中的運輸成本非常重要。

1.2 問題分析

即時配送的貨物主要為小型且分散，且不同入口訂單來源的需求要滿足多元化需求，整體呈現出一個動態的變化過程，現實中即時配送訂單分配未按照一定的規范標準，同類型以及需求點相近的產品或有特殊需求的產品用戶，比如有時間窗要求或要求增值服務的，未被合理分配在一起。即時配送的貨物大多為三公里之內的貨物，在智能化配送未完全普及的背景下，人工配送是主要的配送方式，而人工配送的路徑并未完全運用智能化算法來分析配送路徑的選擇以及順序，大多依賴于配送員主觀上的認知，這些在很大程度上影響即時配送效率。

1.3 模型假設

1.3.1 問題假設

生鮮產品不區分種類，按照訂單分配；假設生鮮產品初始配送新鮮度以及耐腐性能無差別；配送地點產品充足，不存在因產品短缺而引起的時間浪費；挑揀人員熟悉門店環境，可以及時挑揀；配送車輛統一出發，不考慮多時段車輛配送；配送過程中始終勻速行駛，不考慮行駛路程中突發因素對車輛速度的影響；假設配送過程中不發生堵車、車禍等意外情況；配送過程中的行駛速度是恒定的，不隨路況發生變化；配送過程中配送車輛溫度恒定，不受其他因素影響。

1.3.2 約束條件

配送車輛從生鮮產品配送中心出發，完成配送后返回配送中心；配送中心貨物充足，能滿足一切訂單需求；每輛車輛載重量大于當車訂單需求量；配送車輛實現眾包配送，但訂單需求方只能由一個配送車輛完成。

1.3.3 變量設置表

訂單聚類中心I，配送中心O，需求點集合M={i},i=1,2,3,…,n，配送點集合N={J},J=1,2,3,…,n，運輸車輛的集合K={k},k=1,2,3,…,n，需求點i 到配送點j 的距離dij，訂單i 的需求量Ri，車輛k 載重量Zk，客戶可接受配送時間[Ei,Li]，時間滿意度程度M（t），生鮮產品在t 時間的新鮮度H（t），生鮮農產品的變質率α。

2 數學模型構建

2.1 相似性函數

由于新零售模式的影響，更多的消費者傾向于通過線上購買物品，因此產生訂單的位置是多樣性的，配送端需要盡可能用最少的人力、物力、財力實現即時配送。K-means 聚類算法以需求點相距距離作為相似性的評價指標，以多個配送中心和分散需求點進行聚類，其結果受到K 值選取的影響，容易超出劃定的配送范圍，增加尋優的復雜過程。此算法契合于即時配送確定范圍內的尋優問題。

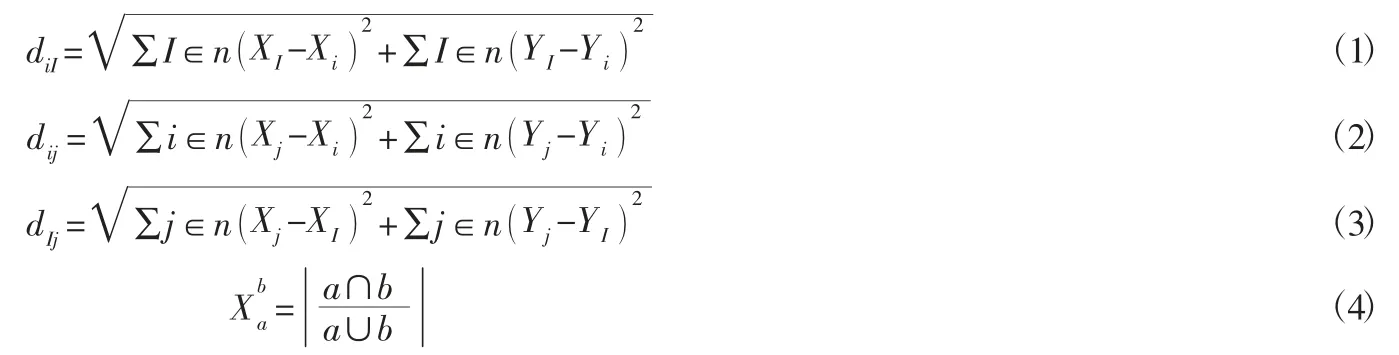
Step1：計算各需求點，配送中心，聚類中心之間相互的距離，diI表示需求點與聚類中心的距離，dij表示需求點到配送中心的距離，dIj表示配送中心到聚類中心的距離，（Xi,Yi）表示需求點坐標，（XI,YI）表示聚類中心坐標，（Xj,Yj）表示配送中心位置坐標。

Step3：更新訂單位置，重新計算Step1，Step2，直至訂單穩定，結束迭代。

2.2 懲罰成本

由于配送時間的限制性而產生一種懲罰成本，懲罰成本大小表示顧客對于即時配送時間的滿意程度，兩者之間的關系是此消彼長，密不可分的，CC表示懲罰成本，ε1,ε2表示早到或晚到客戶點的時間懲罰系數，因此懲罰成本可表示為：

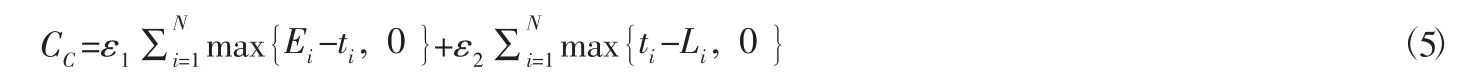
2.3 貨損成本

產品新鮮度對于顧客的回頭率具有非常重要的作用，本文引入新鮮度函數來體現生鮮農產品的貨損成本，生鮮產品的新鮮度會隨著配送時間和溫度的變化而變化，假設生鮮超市農產品物流配送過程中可以保證產品恒溫運輸，α 為變質率，且為固定常數，H（t）表示生鮮農產品從配送中心O 到需求點i 中即時配送過程中發生的新鮮度變化。

當t=0 時，H（t）=1，此時生鮮農產品從配送點開始裝車出發，假定新鮮度為1，經過運輸過程中耗費的時間t，新鮮度逐漸下降，由此表現出遞減的指數函數。

根據生鮮農產品需求量與下降的新鮮度成線性關系的假設，只考慮訂單運輸過程中的貨損成本，P 為貨物單價，α 表示生鮮產品貨損率，ti表示配送車輛Ki行駛到訂單i 的時間，t0表示配送車輛Ki從配送中心出發的時間，則貨損成本為：

2.4 運輸成本

生鮮產品從集中生產場所流入分散需求點主要通過物流配送來實現，在配送過程中成本支出最大的部分就是運輸成本，運輸成本始終貫穿配送的每一時刻，在企業經濟效益中占據重要地位，受物流運輸距離，車輛行駛速度等主要因素影響。忽略供應商到配送中心的距離，考慮從配送中心到需求點再到配送點的距離下的固定成本和車輛運輸成本。

因此，建立目標函數模型：

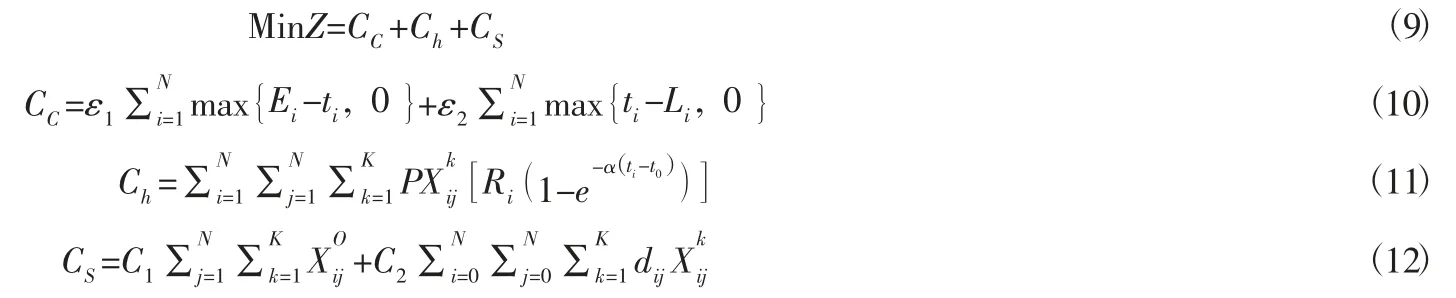
目標函數表示以總配送成本最小，具體又包括以訂單分類影響的訂單分類標準和配送時間，運輸過程中產生的運輸費用，貨損費用，懲罰費用。

約束條件：

約束（13）表示多個訂單需求量小于配送車輛載重量；約束（14）表示每個客戶只被一個配送車輛配送；約束（15）表示車輛從配送中心出發到完成配送，并返回配送中心；約束（16）表示第k 輛配送車輛從第i 個需求點到第j 個配送點的概率，或0，1 代表配送，0 代表不配送；約束（17）Yki表示第k 輛車到第i 個需求點的概率，Yki=1 或0，1 代表配送，0 代表不配送。

3 粒子群算法模型

物流配送路徑優化問題屬于多變量、多目標的復雜線性問題，物流配送路徑優化方法主要有精確算法和啟發式算法兩類。這兩類方法又包含蟻群算法、遺傳算法、粒子群算法、模擬退火算法以及禁忌搜索算法等，蟻群算法適用于多目標的優化問題，遺傳算法適用于更復雜類型的優化問題，粒子群算法參數設置較簡單，更適用于多峰高維的復雜計算問題[10-12]。但他們本身又具有一定的局限性，比如在粒子群算法全局搜索過程中易早熟收斂、陷入局部最優，需提出改進后的粒子群算法，克服粒子群算法的不足，能更好地解決配送路徑問題。

3.1 粒子編碼方式

在粒子群算法尋優過程中，每個粒子都代表著需求點被選的隨機性，假設粒子維度v 與需求點數量n 相等，每個維度數代表相應待選擇的需求點，Xi表示粒子i 的第一維編碼原始值，原始值在[1,n] 內變化，相同的整數部分表示同一車輛配送，小數部分的數值大小表示配送的先后順序，Ki表示粒子i 的第二維編碼值，代表需求點選取的車輛編號，本文選取盒馬生鮮12個需求點的實際位置坐標，按照數值越小越先配送的原則，進行編碼排序，以配送中心作為初始聚類，則初始種群的配送方案（粒子）的編碼和解碼如表1 所示。

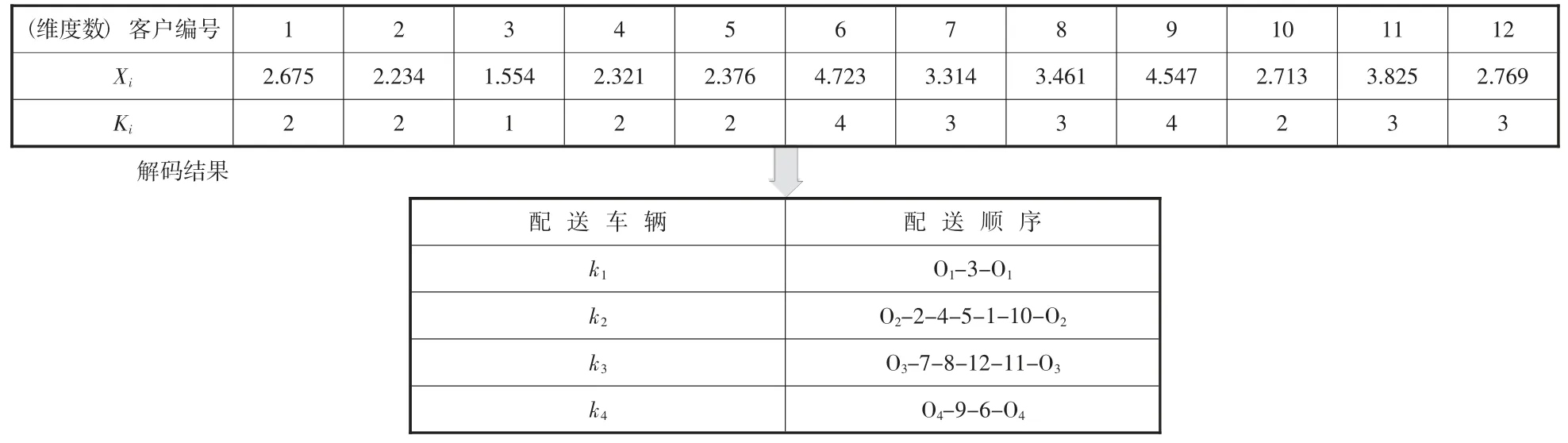
表1 配送中心與粒子間的映射關系

粒子從多個配送中心出發，逐步訪問各需求點位置、時間窗要求、商品新鮮度接受程度及配送車輛最大承載量，各需求點僅被訪問一次，訪問結束后返回配送中心。根據粒子形成的位置記憶，對需求點訂單進行順序編碼和解碼，如12 個需求點和3輛配送車輛的順序解碼后形成的配送順序分別為車輛k1配送O1-3-O1；車輛k2配送O2-2-4-5-1-10-O2；車輛k3配送O3-7-8-12-11-O3,車輛k4配送O4-9-6-O4。如圖1 所示。

圖1 多配送中心配送方案

3.2 改進粒子群算法

3.2.1 自適應慣性權重

根據K-means 把多個配送中心轉化為單個配送中心求解，需求點i 到聚類中心I 的距離很大程度上是由距離慣性權重來決定的，粒子設置相應的適應度值，調整權重大小，對于路徑優化有重要作用，因此適應度函數如式（18）所示：

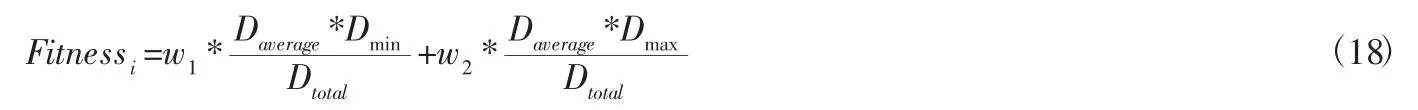
其中：w1,w2表示權重因子，且因即時配送的生鮮產品大部分為三公里之內的訂單，則有w1+w2=1,w1＞w2,Daverage表示需求點i 的平均配送距離，Dmin表示各需求點i 最低配送距離，Dmax表示最長配送距離，Dtotal表示各需求點i 總配送距離。

3.2.2 粒子位置，速度更新

實時更新粒子位置，速度粒子的位置和速度對于粒子群算法的選優過程占有重要地位，他們不僅能解決粒子陷入局部最優的局面，而且快速縮短尋優過程的時間以及準確度的提高，本文在更新粒子位置和速度時把訂單產生的隨機性考慮在內，不同的時間段會有新的訂單取消和產生，更加準確設置合理的路徑。

粒子位置更新：

粒子速度更新：

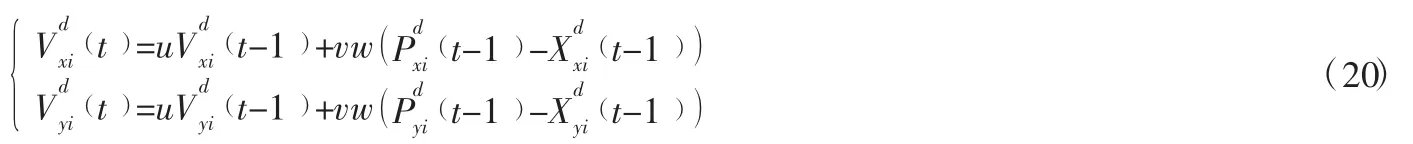
3.3 改進算法步驟

設置參數，輸入需求點時間窗，位置坐標，假設車輛個數為n，求解的最大迭代次數為imax，本文取值200，當前迭代次數t=0，首先，初始化粒子的速度和位置，即明確需求點位置，根據K-means 聚類算法和訂單相似性對訂單進行合理劃分，其次，按照上述得出的目標函數計算粒子的適應值，降低即時物流配送總成本。在相應的約束條件下得出單個粒子最優值pbest和群體最優值gbest，確定粒子初始最優解，逐步迭代，同時改進智能算法，直至迭代次數最大，完成路徑優化。具體算法過程如圖2所示。

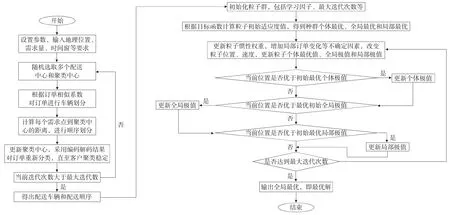
圖2 算法過程

首先，對訂單開始聚類分析：

Step1：輸入客戶基本信息，比如位置信息、時間窗要求等；

Step2：隨機選取多個配送中心和聚類中心；

Step3：利用K-means 算法解鎖粒子編碼，根據訂單相似性分配車輛，完成分批配送劃分，并按照孰近原則劃分先后順序，持續更新需求點訂單，直至訂單相對趨于穩定，得出配送車輛和配送順序的合理分配，否則返回Step2，重新迭代；

Step4：初始化種群，選擇客戶，引入算法，設置種群規模N，最大迭代次數imax，權重因子w1,w2等；

Step5：按照即時配送數學模型，計算每個粒子的適應度值，尋找種群粒子個體最優位置bpest和群體全局最優位置pbest；

Step6：更新粒子位置、速度、慣性權重，產生的個體最優和全局最優替代原來產生的個體和全局最優；

Step7：滿足迭代次數，若是，則輸出結果，若否，則Step6，重新執行粒子優化策略，直至迭代結束，得到全局最優解。

4 案例分析—盒馬生鮮

4.1 案例基本情況

以某市某區域盒馬生鮮即時物流配送為例，研究改進后的智能算法對物流即時配送的成本影響和效率影響，并提出相應意見，具體案例相關數據設置如表2、表3 所示。

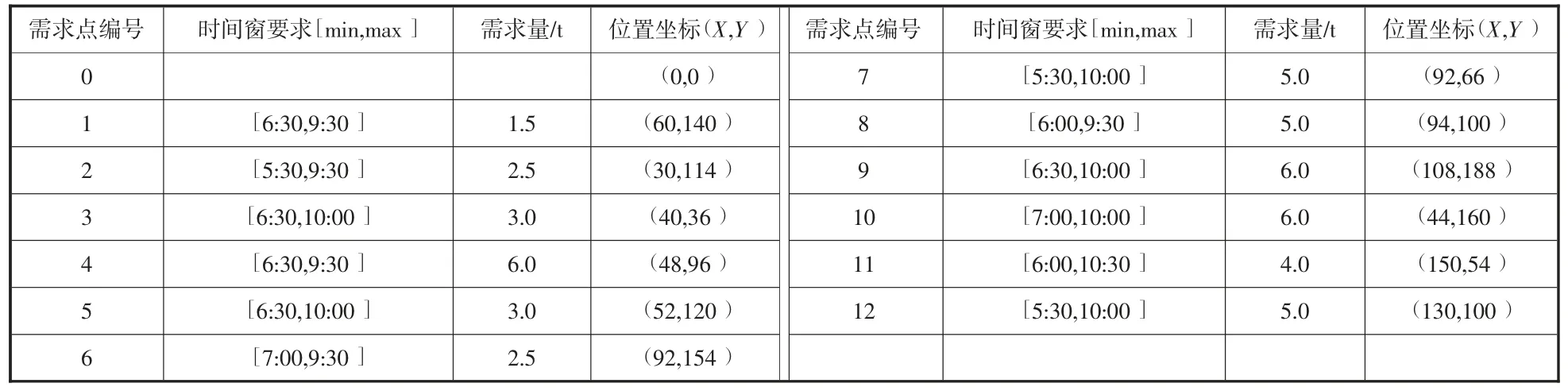
表2 用戶點位置和時間窗要求

表3 相關參數設置

4.2 模型求解

本文將多個配送中心配送轉化成多個單配送中心出發，再利用K-means 算法選取其中一個需求點i 為聚類中心，粒子從聚類中心I 配送出發，逐步訪問各需求點位置、時間窗要求、商品新鮮度接受程度以及配送車輛最大承載量，各需求點僅被訪問一次，訪問結束后更新需求點信息直至穩定形成位置記憶，最后返回配送中心。以需求點1 作為更新的聚類中心，解碼結果如表4 所示：

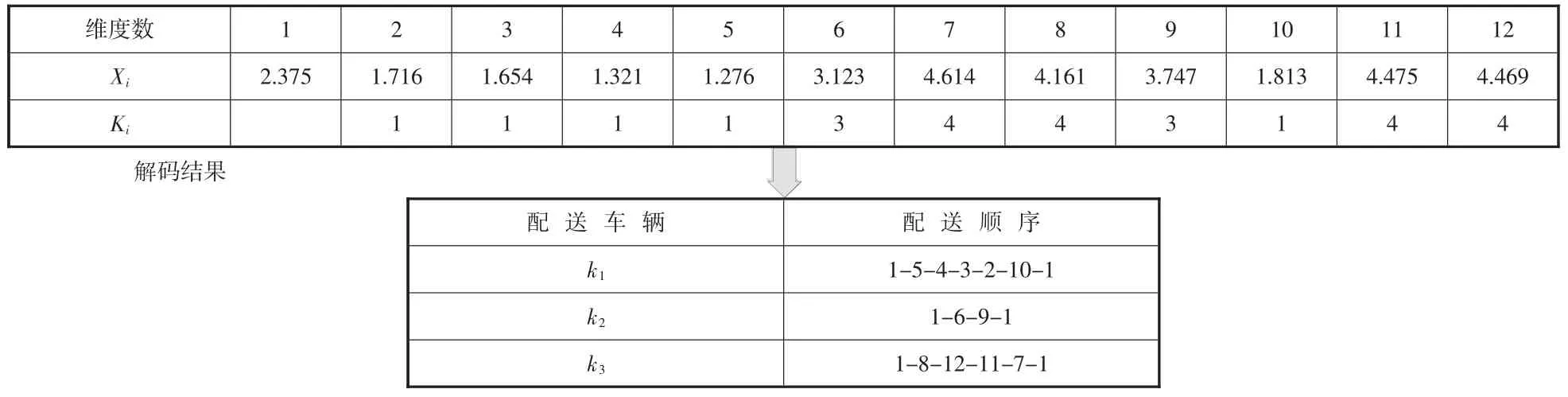
表4 聚類中心與粒子間的映射關系

根據粒子形成的位置記憶，對需求點訂單進行順序編碼和解碼，形成的配送順序分別為車輛k1配送1-5-4-3-2-10-1；車輛k2配送1-6-9-1；車輛k3配送1-8-12-11-7-1，由圖3 所示。

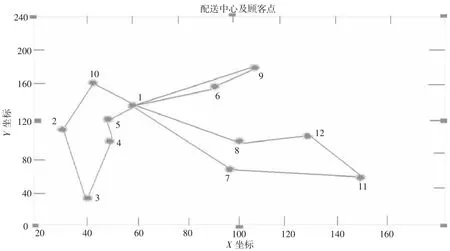
圖3 聚類中心配送方式

4.3 算法比較

表5 改進算法對目標函數的影響

表6 改進算法與傳統算法對比

5 結論

由此可知，注重物流運輸效率、加強管理上的模式，提高物流服務質量，優化粒子適應度值，改變粒子慣性權重，更新粒子位置和速度對于粒子的尋優過程至關重要，不僅有效避免粒子陷入局部最優，同時又能保證整個尋優過程高速、準確進行，提升客戶滿意度，高效完成訂單配送。優化訂單的劃分標準，注重訂單的個性化服務，以及特殊需求，提高客戶滿意度，最終降低536 元配送總成本，提高12%的配送效率。