考慮加載歷史多因素耦合作用下的梁軌相互作用附加力

于向東，黃錚，敬海泉,

(1. 中南大學 土木工程學院，湖南 長沙 410075；2. 中南大學 高速鐵路建造技術國家工程實驗室，湖南 長沙 410075)

對于無縫線路上的梁軌相互作用問題，以往的大多數研究以及各國規范均采用的是各種荷載單獨作用下的結果進行代數求和的線性疊加法，并沒有考慮加載歷史的影響[1-5]。然而，梁軌相互作用是非線性問題，多個荷載組合時存在一個加載順序，也就是加載歷程，因此線性疊加法得到的數據必然與真實結果有一定誤差[6-7]。目前已有部分研究在梁軌相互作用分析中考慮了加載歷史的影響。石龍等[6]建立了考慮加載歷程的城市軌道交通簡支高架橋梁軌相互作用模型，研究表明其鋼軌縱向附加力較線性疊加法有所降低并且在循環荷載作用后存在收斂的殘余力；RUGE等[7-8]在梁軌相互作用分析中考慮了加載歷史并模擬了梁軌相互作用非線性變化過程，論證得出考慮加載歷史能夠顯著降低鋼軌最大壓應力；ZHANG等[9]提出一種考慮不同荷載工況下扣件的加載歷史效應和縱向阻力變化的非線性梁軌相互作用分析模型，研究發現扣件計算方法和縱向阻力位移曲線對鋼軌附加應力和梁軌相對位移有很大影響；LUO等[10]提出一種考慮加載歷史的扣件縱向阻力變化規律模型，并與RUGE模型[7-8]和理想彈塑性阻力模型進行比較，驗證了其模型的力學行為與試驗結果更接近；閆斌等[2,11-12]以高速鐵路梁橋和斜拉橋為例，建立梁軌相互作用有限元計算模型，計算了墩頂水平力、鋼軌應力及位移，與線性疊加法進行了比較，發現考慮加載歷史的計算結果偏小并更接近于實際情況。上述研究均是以梁橋或斜拉橋為研究對象來考慮加載歷史對梁軌相互作用的影響，對于大跨度懸索橋的研究還存在不足。以往研究采用的線性疊加法，對于各種荷載耦合的情況，僅是對各個荷載的作用單獨計算，隨后直接將各個荷載計算結果線性疊加。而對于懸索橋這種大跨度橋梁，溫度等其他荷載之間的耦合作用對其鋼軌縱向力和梁軌相對位移的影響無法通過線性疊加法準確地展現[13-16]。另外，懸索橋上的梁軌相互作用具有非線性的特性，在線路縱向阻力具有滯回特性的前提下，往復荷載及循環荷載作用后，必然存在一定的殘余變形，產生鋼軌殘余應力，這是線性疊加法無法獲取的。因此，本文以五峰山懸索橋為研究對象，通過考慮加載歷史的方法，計算鋼軌在溫度、撓曲及制動荷載耦合作用下的縱向附加力，以及在往復荷載與循環荷載作用下的鋼軌殘余應力，與線性疊加法結果進行分析比較。

1 考慮加載歷史的有限元模型

1.1 計算參數

五峰山長江大橋是我國目前已建成運營的最大跨度的公鐵兩用懸索橋。大橋設置雙層橋面，上層為8車道公路，下層為四線鐵路。其主橋為雙塔連續鋼桁梁懸索橋，跨徑布置為(84+84+1 092+84+84) m，全長1 428 m，主橋兩側分別接上4×57.2 m的混凝土連續梁引橋，總長度為1 892 m。全橋采用兩平行主纜，橫向中心距43 m，主跨矢跨比1/10。其全橋立面如圖1所示。

圖1 懸索橋全橋立面圖Fig. 1 Elevation of the whole suspension bridge

1.2 線路縱向阻力本構模型

該橋鋪設鋼軌類型為CHN60[17]型，鋼軌與主梁之間采用有砟軌道Ⅲ型枕。因此，本文采用《鐵路無縫線路設計規范》[5]規定的圖2所示有砟軌道縱向阻力模型來模擬線性疊加法結果。該模型規定在無豎向荷載及有載時車輛下的最大道床阻力為15 kN/m/線，有載時機車下最大道床阻力為23.2 kN/m/線，彈塑性臨界位移均為2 mm。

圖2 有砟軌道縱向阻力模型Fig. 2 Longitudinal resistance model of ballasted track

對于考慮加載歷史的梁軌相互作用分析，不能使用圖2所示的道床縱向雙線性模型，否則會產生問題。以往復荷載為例，即對結構先進行加載而后卸載，假如道床阻力在加載時進入到塑性狀態，那么在卸載時，由于施加的是大小相等、方向相反的荷載，按照雙線性模型的理論，道床的位移和阻力都會沿著來時的路徑回到初始狀態。然而由于線路縱向阻力具有滯回特性，在阻力曲線進入到塑性階段后鋼軌必然會存在一定的殘余變形，產生殘余應力，因此雙線性模型不能再適用。這也表明單次加載的阻力曲線并不能用來表示結構在往復荷載作用下的道床縱向阻力性能，而線性疊加法的本質就是將各工況單次加載的結果進行簡單的線性相加來表示多荷載共同作用的結果，因此對于多荷載共同作用的情況下需要考慮加載歷史。由于理想彈塑性滯回阻力模型具有滯回特性，用它來模擬道床縱向阻力更加符合實際情況，本文采用該模型來模擬考慮加載歷史法計算各荷載工況產生的附加力。如圖3所示，該模型在《鐵路無縫線路設計規范》[5]的雙線性模型的基礎上考慮了滯回特性，橫坐標表示梁軌縱向相對位移，縱坐標表示道床縱向阻力，將最大縱向阻力設為15 kN/m/線，最大線位移設為2 mm。

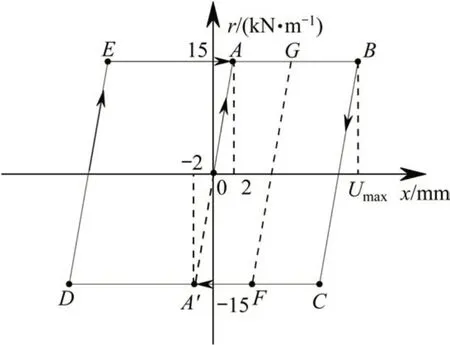
圖3 道床縱向阻力理想彈塑性滯回模型Fig. 3 Ideal elastoplastic hysteretic model of longitudinal resistance of track bed

1.3 梁軌相互作用有限元模型

基于通用有限元軟件Ansys，建立了如圖4所示沿橋梁縱向(x方向)由引橋混凝土梁、軌道、鋼桁梁、主纜、吊桿、塔架和橋墩組成的梁軌相互作用計算模型。將整座橋分為橋面系統、塔墩、纜索來建立模型，建立橋面系統時，采用BEAM4單元模擬鋼軌、鋼桁梁與引橋混凝土梁，橋面鋪裝及橋面板等效為荷載加到橋梁上；建立塔墩時，同樣采用BEAM4單元模擬橋墩和主塔；建立纜索時，采用LINK10單元模擬主纜和吊索。采用線性彈簧單元COMBIN14模擬橋梁支座、線路豎向和橫向阻力，對于線路的縱向阻力則采用能夠考慮縱向阻力滯回特性的非線性彈簧單元COMBIN39來模擬，采用BEAM4梁單元來模擬阻尼器的制動作用。在邊界條件上，主纜的錨固點和塔墩墩底均固結，不約束主塔頂部順橋向平動自由度。另外，懸索橋主橋兩梁端均應設置鋼軌伸縮調節器，但是，為了揭示懸索橋上無縫線路受力和變形的規律，尤其是主橋梁端的應力變化情況，以下的研究均不在梁端設置鋼軌伸縮調節器。

圖4 懸索橋梁軌相互作用計算模型Fig. 4 Calculation model of track-bridge interaction of suspension bridge

2 計算結果

2.1 多荷載耦合作用結果分析

對于多荷載耦合作用，采用溫度與撓曲荷載耦合、撓曲與制動荷載耦合、溫度撓曲和制動荷載耦合情況對比線性疊加法與加載歷史法的鋼軌縱向附加力。參照《鐵路無縫線路設計規范》[5]，溫度變化采用懸索橋鋼桁梁升溫25 ℃，引橋混凝土梁升溫15 ℃，降溫數值與升溫相同；列車豎向荷載取ZK活載，列車荷載加載長度根據《高速鐵路設計規范》[18]取為550 m，加載范圍如圖1所示(從主跨跨中向3號塔方向加載)；對于列車制動荷載，按照規范輪軌黏著系數取0.164，加載長度仍為550 m，范圍同撓曲荷載即從主跨跨中向3號塔方向加載。其中溫度荷載僅考慮升溫荷載的情況，應力圖中豎直虛線為兩主塔中心線。

2.1.1 3種耦合情況的結果

由圖5(a)可知，加載歷史法與線性疊加法沿線路縱向的應力分布趨勢總體一致。在主橋中跨鋼軌受拉且2種計算方法計算的鋼軌應力數值接近，加載歷史法與線性疊加法鋼軌最大拉應力值分別為93.36 MPa和90.73 MPa，兩者僅相差約3%；而在兩主塔外側承受較大壓應力且2種計算方法在主橋小里程梁端處即鋼軌坐標為-171.2 m處的鋼軌應力分布差異明顯，加載歷史法計算的鋼軌最大壓應力為265.97 MPa，相較線性疊加法計算的鋼軌最大壓應力低約24%。由圖5(b)可知，考慮加載歷史后小里程及大里程固定墩的墩頂水平力分別較線性疊加法降低約16%和57%。

圖5 升溫與撓曲荷載耦合對比Fig. 5 Comparison of temperature rise and deflection load coupling

由圖6(a)可知，因撓曲與制動荷載加載區域靠近北塔，故除了主橋小里程梁端處2種計算方法應力分布不同，其他位置上2種計算方法計算的鋼軌應力數值接近。其中加載歷史法與線性疊加法下鋼軌最大拉應力出現在主橋大里程梁端處即鋼軌坐標為1 263.2 m處，分別為70.74 MPa和70.09 MPa，僅相差1%；最大壓應力出現在北側主塔處，分別為56.04 MPa和56.14 MPa。墩頂水平力相較于鋼軌應力的變化則較大，由圖6(b)可知，考慮加載歷史后小里程及大里程固定墩的墩頂水平力分別較線性疊加法降低約29%和7%。

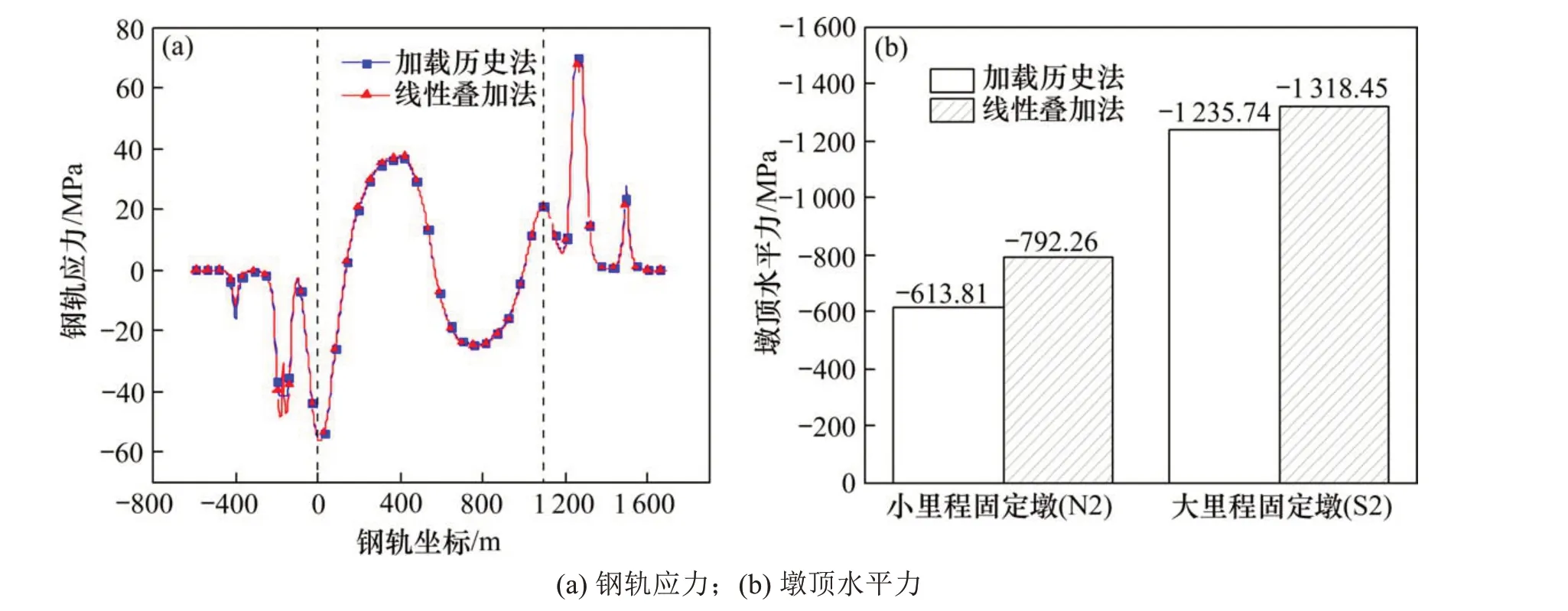
圖6 撓曲與制動荷載耦合對比Fig. 6 Comparison of deflection and braking load coupling

由圖7(a)可知，2種計算方法鋼軌應力分布的主要差別還是集中在主橋兩梁端附近。在主橋中跨區域鋼軌受拉，加載歷史法與線性疊加法鋼軌最大拉應力值分別為91.28 MPa和88.21 MPa，兩者僅相差約3%；在兩主塔外側鋼軌大部分處于受壓狀態，加載歷史法與線性疊加法最大壓應力均出現在主橋小里程梁端處，加載歷史法計算的鋼軌最大壓應力為208.67 MPa，相較線性疊加法計算的鋼軌最大壓應力265.31 MPa低約27%。由圖7(b)可知，考慮加載歷史后小里程及大里程固定墩的墩頂水平力分別較線性疊加法降低約26%和29%。

圖7 升溫、撓曲和制動荷載耦合對比Fig. 7 Comparison of temperature rise, deflection and braking load coupling

2.1.2 考慮加載歷史的結果分析

通過以上對鋼軌應力極值和墩頂水平力的比較，對于加載歷史法和線性疊加法綜合各耦合情況的結果可以得出以下結論。

1) 2種計算方法下鋼軌拉應力與壓應力在全橋分布的區域相同，僅在數值上有局部的差異，特別是在主橋梁端局部范圍內鋼軌應力值有明顯差異；

2) 線性疊加法對鋼軌應力及墩頂水平力的計算結果與加載歷史法相比較為保守。在最大拉應力方面，加載歷史法較線性疊加法的計算結果普遍增大，但是最大增幅僅為3%；而在最大壓應力方面，線性疊加法較加載歷史法的計算結果普遍增大，鋼軌應力最大增幅可達27%；在墩頂水平力方面，線性疊加法結果普遍高于加載歷史法，最大增幅可達36%；

3) 因梁軌相對位移差別與鋼軌應力的差別具有一致性，可知2種方法的梁軌相對位移總體上差別較小，只是局部區域的梁軌相對位移還是有明顯差距的，但是墩頂水平力卻呈現出更大的變化幅度，這主要是線性疊加法使得同向疊加的墩頂水平力拉大了與加載歷史法的差距，而反向疊加的墩頂水平力有時會因數值相對較小而呈現出比加載歷史法更大的增幅造成的；

4) 同撓曲和制動荷載相比，溫度荷載對于鋼軌縱向應力與墩頂水平力的產生起著主要的貢獻作用。以加載歷史法下鋼軌應力極值為例，在未施加溫度荷載時鋼軌最大壓應力僅為56.04 MPa，而施加上溫度荷載后，其最大壓應力增加為208.67 MPa，增幅達到了272%。

2.2 往復荷載作用下結果分析

本節分別研究溫度、撓曲及制動往復荷載在線性疊加法和加載歷史法下計算出的鋼軌殘余應力及位移，圖8中兩豎直虛線為兩主塔中心線。

2.2.1 溫度往復荷載

以橋梁在白天升溫、夜間降溫模擬溫度往復荷載。圖8(a)為線性疊加法的鋼軌殘余應力值，圖8(b)～圖8(d)為加載歷史法的梁軌相互作用結果。采用線性疊加法計算升溫和降溫作用可以相互抵消，最終鋼軌殘余應力為0，其升溫單項荷載最大值可達到223 MPa，與不設伸縮調節器時218 MPa的鋼軌應力[19-20]相差不大，且鋼軌伸縮調節器只對主橋梁端范圍鋼軌應力有較大影響，其余部分的影響幾乎可以忽略。在考慮加載歷史后，在兩主塔外側還存在很大的鋼軌殘余應力且波動劇烈，鋼軌最大殘余應力為拉應力，位于主橋梁端處，達到91.27 MPa，可達到升溫單項荷載應力最大值的41%；主橋中跨區域鋼軌殘余應力分布均勻且數值很小，總體上鋼軌殘余應力以主橋跨中呈對稱分布。鋼軌殘余位移和梁軌殘余相對位移以主橋跨中呈反對稱分布，兩主塔外側殘余相對位移變化劇烈，最大梁軌殘余相對位移達到22.17 mm；主橋中跨梁軌相對位移接近于0，從而也證明這一區域鋼軌殘余應力數值同樣接近于0。

圖8 溫度往復荷載下鋼軌殘余應力及位移Fig. 8 Rail residual stress and displacement under temperature reciprocating load

2.2.2 撓曲往復荷載

以列車駛入橋梁隨后駛離，即對橋梁進行豎向加卸載模擬撓曲往復荷載。圖9(a)為線性疊加法的鋼軌殘余應力值，圖9(b)～圖9(c)為加載歷史法的梁軌相互作用計算結果。采用線性疊加法時主橋梁端處存在殘余應力，其最大值為10.89 MPa，約為撓曲單項荷載作用下(115.50 MPa)的9%。考慮加載歷史后，主橋梁端附近鋼軌殘余應力波動劇烈，鋼軌最大殘余拉應力為30.05 MPa，為撓曲單項的26%，相比于溫度往復荷載作用下91.27 MPa的殘余應力減少2/3。梁軌殘余相對位移在主橋梁端也發生波動，但波動幅度沒有溫度往復作用的劇烈，最大梁軌殘余相對位移為5.34 mm，這也說明相對較大的梁軌殘余相對位移是產生較大的鋼軌殘余應力的原因。

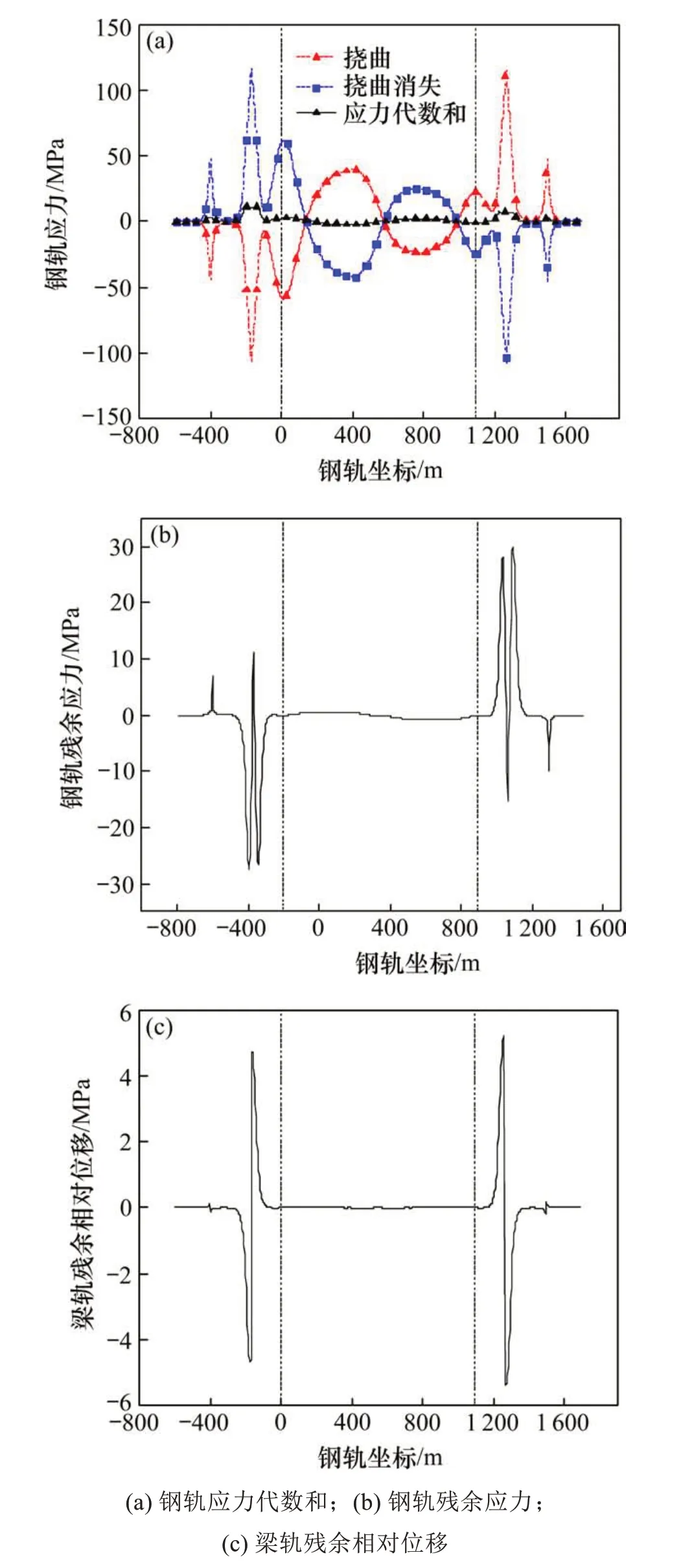
圖9 撓曲往復荷載下鋼軌殘余應力及位移Fig. 9 Rail residual stress and displacement under deflection reciprocating load

2.2.3 制動往復荷載

以列車在橋上制動然后停止，即先后施加制動力與反向制動力模擬制動往復荷載。圖10(a)為線性疊加法的鋼軌殘余應力值，圖10(b)～圖10(c)為加載歷史法的梁軌相互作用計算結果。

圖10 制動往復荷載下鋼軌殘余應力及位移Fig. 10 Rail residual stress and displacement under braking reciprocating load

采用線性疊加法計算制動往復作用鋼軌殘余應力接近于0，考慮加載歷史后，由于制動力加載位置靠近北塔小里程端，故應力及位移峰值均出現在左側梁端，鋼軌最大殘余拉應力為9.65 MPa，占制動荷載單獨作用下(64.63 MPa)的15%，僅占溫度往復作用最大殘余應力的11%。最大梁軌相對位移為1.17 mm，也僅占溫度往復作用的5%。

2.3 循環荷載作用下結果分析

當將多種往復荷載連續施加就形成了循環荷載。橋梁必然會經歷循環荷載的作用，本節研究循環荷載作用下鋼軌應力及位移的變化情況。

2.3.1 單項循環荷載

圖11～13給出溫度、撓曲和制動3種荷載循環作用下的鋼軌殘余應力，圖中的兩豎直虛線為主橋兩主塔中心線。表1給出3種循環荷載作用下鋼軌殘余應力的最大及最小值匯總。

由圖11～13以及表1可見，在鋼軌經歷過一次循環荷載后，就能夠達到較穩定的收斂值，這是道床縱向阻力的彈塑性滯回特性造成的。以溫度循環荷載為例并結合圖3說明：在梁相對于軌道升溫后，在兩主塔內側的懸索橋主跨區域梁軌相對位移接近于0，小于2 mm的彈塑性臨界位移，這一區域大部分道床縱向阻力處于彈性狀態(圖3中OA段)；兩主塔外側梁軌相對位移遠大于2 mm，道床縱向阻力處于塑性狀態(圖3中的B點)。之后梁相對于軌道降溫，處于彈性狀態的部分可沿OA路徑彈性恢復，處于塑性狀態的部分不能再沿著升溫時的路徑恢復，而是沿著與OA段平行的BC路徑彈性恢復；因升降溫幅度相同，故處于彈性狀態的部分最多可以恢復到O點，而處于塑性狀態的部分，由于其道床縱向阻力必然可以進入到反向的塑性狀態，故其道床阻力-位移曲線會沿著BCA＇段恢復至F點，產生明顯的殘余相對位移，這也是往復荷載作用后鋼軌應力不能抵消的原因所在。之后無論再經歷幾次溫度循環荷載的作用，處于彈性部分的道床縱向阻力-位移曲線都只會在OA線段上往復滑動，并且每經歷過一次往復荷載作用，其縱向阻力都會穩定地恢復到O點；處于塑性部分的道床縱向阻力-位移曲線則會沿著FGBCF線段往復滑動，并且每經歷過一次往復荷載作用，其縱向阻力都會穩定地恢復到F點。

表1 鋼軌殘余應力最值匯總表Table 1 Summary of maximum residual stress of rail

圖11 溫度循環荷載下鋼軌殘余應力Fig. 11 Residual stress of rail under temperature cyclic load

2.3.2 多荷載耦合作用下的循環

在實際情況中更多出現的是多項往復荷載耦合的循環荷載共同作用在橋梁上，因此為了了解梁軌相互作用系統中鋼軌殘余應力及變形的情況，需要讓橋梁依次經歷升溫、撓曲往復荷載、撓曲、制動往復荷載、撓曲消失和降溫的加載過程，得出鋼軌殘余應力及位移結果如圖14所示，圖中兩豎直虛線為中跨兩主塔中心線。

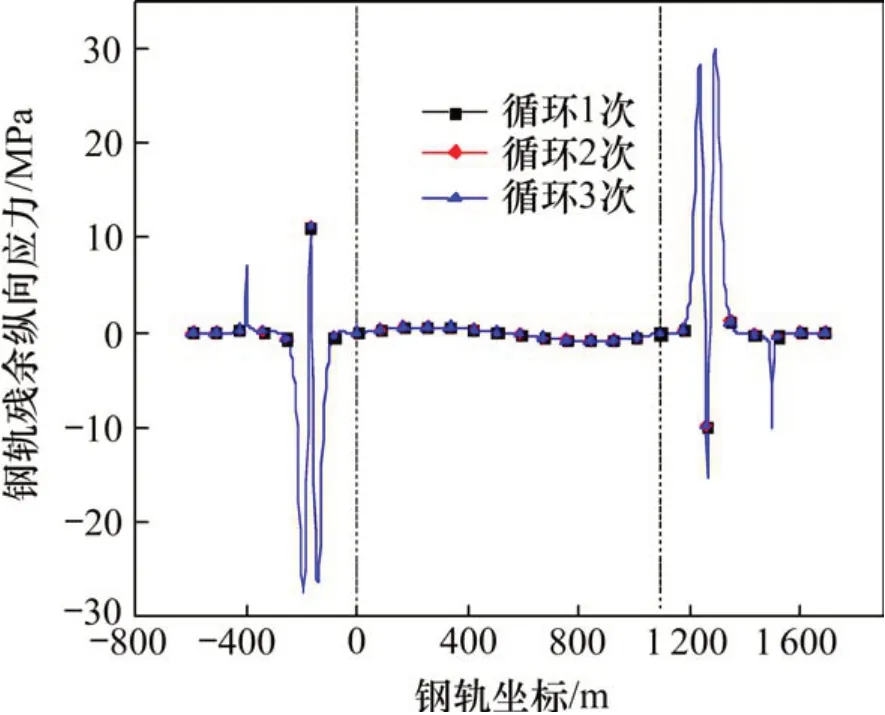
圖12 撓曲循環荷載下鋼軌殘余應力Fig. 12 Residual stress of rail under deflection cyclic load

圖13 制動循環荷載下鋼軌殘余應力Fig. 13 Residual stress of rail under braking cyclic load

圖8(b)～8(d)與圖14(a)～14(c)的變化趨勢相似，圖8(b)和圖14(a)加載歷史法得出殘余應力最大值分別為91.27 MPa和99.53 MPa，二者僅相差9%，圖14(c)所示的梁軌殘余相對位移與溫度往復荷載下梁軌殘余相對位移變化趨勢一致，但是最大殘余相對位移由溫度往復荷載下的22.17 mm增大到了30.58 mm。多循環荷載耦合下的鋼軌殘余位移則是由于撓曲和制動荷載非對稱加載，使其較溫度往復荷載在負方向增大，不過鋼軌位移的升降趨勢仍與溫度往復荷載保持一致。因此，在多項循環荷載耦合的情況下，其鋼軌殘余應力與梁軌相對位移仍然是以溫度往復荷載下的結果為主，撓曲與制動荷載對鋼軌殘余應力及位移的影響均較小。

圖14 2種方法多循環荷載耦合對比Fig. 14 Multi cycle load coupling comparison of two methods

2.4 計算結果對比分析

以上分析表明，對于溫度、撓曲和制動荷載耦合工況下，懸索橋上采用線性疊加法計算的鋼軌縱向附加力與加載歷史法相比，偏大1%～27%，而線性疊加法計算出的墩頂水平力與加載歷史法相比誤差則較大，這些結果與簡支梁橋、連續梁橋和斜拉橋[2,11-12]的鋼軌附加力和墩頂水平力變化規律非常相似，說明懸索橋與梁橋和斜拉橋在加載歷史法和線性疊加法對比中具有相似規律，證明加載歷史法的計算結果更加符合實際情況；對于3種荷載在往復以及循環作用下，溫度荷載引起的鋼軌殘余應力是最大的，而制動荷載下的鋼軌殘余應力則最小，這與對簡支梁橋[6]的鋼軌殘余應力分析結果有所不同(即制動荷載引起最大而撓曲荷載引起最小)，也說明相比于簡支梁橋，懸索橋上的梁軌相互作用對于溫度變化的響應更加敏感。

3 結論

1) 在多荷載耦合作用下，2種計算方法的鋼軌拉、壓應力分布的總體趨勢相同，但是在數值上線性疊加法計算結果比加載歷史法計算結果更加保守。線性疊加法和加載歷史法鋼軌應力的最大值分別為329.94 MPa和265.97 MPa，增幅可達24%，而墩頂水平力最大值分別為5 959.84 kN和5 123.03 kN，增幅達到36%。

2) 對于溫度、撓曲和制動荷載耦合作用下，溫度荷載對鋼軌縱向應力和墩頂水平力的產生起著主要的貢獻作用。這也證明了溫度荷載對考慮加載歷史的懸索橋上梁軌相互作用有重要影響。

3) 在往復荷載作用下，采用線性疊加法的鋼軌殘余應力計算結果數值較小，而考慮加載歷史后在兩主塔外側鋼軌存在明顯殘余應力，其中溫度往復荷載引起的鋼軌殘余應力明顯大于撓曲與制動往復荷載，達到91.27 MPa，并且達到了升溫單項荷載作用的41%；在主橋梁端存在明顯梁軌殘余相對位移。

4) 在循環荷載作用下，鋼軌殘余應力在一次循環作用后就能快速收斂到穩定值，這是道床縱向阻力的彈塑性滯回特性造成的。在多荷載耦合的循環作用下，對于鋼軌殘余應力與梁軌殘余相對位移的研究可以以溫度往復荷載結果為主。

5) 對于大跨度懸索橋上的梁軌相互作用問題，加載歷史法的計算結果比線性疊加法更加精確。這證明了加載歷史是影響大跨度橋梁梁軌相互作用的一個重要因素。