基于改進自抗擾控制器的磁浮列車速度跟蹤控制研究

王盼盼，楊杰, ，鄒吉強, ，劉鴻恩,

(1. 江西理工大學 電氣工程與自動化學院，江西 贛州 341000；2. 江西理工大學 江西省磁懸浮技術重點實驗室，江西 贛州 341000；3. 國瑞科創稀土功能材料(贛州)有限公司，江西 贛州 341000)

我國磁浮列車發展迅速，目前已有上海高速磁浮線、長沙磁浮快線、北京磁浮線(S1號線)處于商業運營模式。2021年1月，世界首臺高溫超導高速磁浮工程化樣車及試驗線在西南交通大學正式啟用，同年12月，江西理工大學牽頭研發的國際首輛永磁懸浮列車(紅軌“興國號”)順利下線，如圖1所示。針對磁浮列車和高速輪軌列車的速度跟蹤控制問題，國內許多學者對此展開了相關研究，CAO等[1]針對中速磁浮列車的速度跟蹤問題，提出分數階比例-積分-微分控制器(Proportion-Integral-Derivative Controller，PID)，并利用粒子群算法對該控制器參數進行尋優，最后通過仿真實驗驗證了該控制策略的有效性，結果表明分數階PID控制器能夠有效提高列車的跟蹤精度。楊光[2]針對高速磁浮列車運動學模型的非線性特性，將反饋線性化技術與PI控制器相結合作為高速磁浮列車的速度跟蹤控制策略，仿真結果表明此方法能夠使列車很好地跟蹤目標速度曲線，且系統具有良好的魯棒性。嚴細輝[3]針對CRH380AL型動車組的速度跟蹤控制問題，建立了列車的多質點模型，提出模型預測控制與PID相結合的雙模控制策略，仿真結果表明該控制策略能夠提高列車的跟蹤精度。譚暢等[4]針對CRH380AL型列車制動系統的參數不確定性和輸入時滯問題，提出模型參考自適應控制策略，仿真結果表明該控制策略實現了列車對目標速度的漸進跟蹤，提高了列車的制動性能和運行的平穩性。吉鴻海[5]針對高速列車速度跟蹤系統結構的非線性和系統參數的不確定性，提出改進自適應迭代學習控制算法，仿真結果表明該算法能夠有效解決有限時間區間高速列車的速度跟蹤控制問題。李中奇等[6]針對列車運行過程中受到未知干擾的問題，提出基于H∞控制器匹配的廣義預測控制策略，仿真結果表明該控制策略使列車即使在參數突變運行工況下仍具有較高的跟蹤精度、良好的抗干擾能力和很好的魯棒性。宋琦等[7]針對高速列車速度跟蹤系統參數和外界阻力的不確定性，提出一種自適應控制方法，仿真結果表明該控制策略能夠克服列車在運行過程中所受未知外界阻力的不利影響。YANG等[8]針對高速列車運動過程的非線性特性，提出T-S模糊雙線性列車運動學模型和自適應預測控制器，采用惰行學習算法在線調整列車運動學模型和控制器參數，仿真結果表明該方法能夠提高列車的跟蹤精度。自抗擾控制器(Active Disturbance Rejection Controller，ADRC)自被韓京清提出，因其優秀的控制性能已被廣泛運用于各領域[9-10]，國內外眾多學者仍在改進其調參方法，探索該控制器在時滯系統方面的應用，GAO[11]于2003年提出線性化方案，極大簡化了ADRC的調參過程；2020年，YAO等[12]針對多軸同步問題將ADRC與滑模控制相結合，推導出串聯自抗擾控制，并提出一種簡單整定控制器參數的方法。2014年，ZHAO等[13]提出一種基于時滯系統的改進ADRC結構。2020年，ZHANG等[14]針對系統的時滯問題，通過將ADRC與史密斯預估控制相結合，提出一種基于內模原理的參數整定方案。由此看來，針對時滯問題的ADRC控制結構的改進和參數的整定方法值得深入研究。近年來，自抗擾控制在列車的速度跟蹤控制系統方面的應用受到了國內學者的廣泛關注。龍志強等[15]根據磁浮列車軌道線路約束條件以及乘坐舒適性要求，提出利用ADRC進行自動駕駛控制，并通過仿真分析得出，ADRC算法是一種適合磁浮列車運行控制系統要求的算法。WANG等[16]基于貨運列車模型設計了非線性自抗擾控制器算法，并利用人工蜂群算法進行調參，在一定程度上降低了調參的難度。針對高速列車在復雜環境下控制器跟蹤誤差問題，連文博等[17]提出了基于ADRC控制器的高速列車自動駕駛速度控制策略，并利用CRH380A型列車參數進行仿真驗證了自抗擾控制在高速列車速度跟蹤控制問題的適應性，具備抗干擾性強及追蹤誤差小等性能優勢。無論是磁懸浮列車運控問題還是高速鐵路運控問題，ADRC控制均表現出良好的性能優勢，也為本文提供了一定的技術參考。本文在團隊對自抗擾控制和磁浮列車的前期研究的基礎上[16,18]，針對磁浮列車速度跟蹤控制系統的大時滯特性，提出一種基于改進自抗擾控制器(Time-Delay-ADRC，TD-ADRC)的控制策略，并通過傳遞函數等效方法，提出FOPTD模型，并基于此模型，給出了自抗擾控制器的調參方法。最后在MATLAB仿真平臺上分析了此算法相對于其他2種算法的優勢。

圖1 紅軌-“興國號”Fig. 1 Red Rail-“Xingguo”

1 磁浮列車速度跟蹤控制模型基礎

1.1 磁浮列車運動學模型描述

磁浮列車受力狀態簡要可歸納為車輛牽引力、制動力和運行阻力三大部分組成。其中，牽引力與制動力，具有非同時性。運行阻力可包括基本阻力與附加阻力。基本阻力又涵蓋了空氣阻力、車載直線發電機引發的運行阻力和導向軌上的電磁渦流阻力等；附加阻力分為坡道附加阻力和隧道附加阻力，本文僅考慮坡道附加阻力。下面介紹列車的具體的阻力計算公式。

1) 基本阻力

磁浮列車的基本阻力由空氣阻力、車載直線發電機引發的運行阻力和線路兩側導向軌上的電磁渦流阻力阻力3部分組成[19]，以上海高速磁浮列車為例，三者的計算方法如下[2]。

1) 空氣阻力：空氣阻力的大小與磁浮列車的最大截面積、空氣密度和列車表面形狀等有關，與列車的運行速度有關，可用式(1)表示：

式中：Fa為空氣阻力，kN；ν為列車行駛速度，m/s；N為列車編組數。

2) 直線發電機引發的運行阻力：由直線發電機引起的運行阻力與列車的行駛速度和編組車輛數有關，其大小可表示為：

式中：Fc為直線發電機引發的運行阻力，kN；ν為列車速度，m/s；N為列車編組數。

3) 導向軌上的電磁渦流阻力：渦流阻力的大小與磁浮列車的運行速度和車輛編組有關，其表達式為：

式中：Fm為電磁渦流阻力，kN；N為車輛編組數；ν為列車速度，m/s。

2) 附加阻力

附加阻力主要是由于磁浮列車的運行線路情況而造成的額外阻力，線路信息是磁浮列車控制的基礎數據，包含各個路段的限速情況，彎道、隧道、坡道等，本文僅考慮由于坡道而產生的坡道附加阻力。

坡道附加阻力有正負之分，當磁浮列車在下坡道運行時，坡道附加阻力為磁浮列車提供動力，此時數值為負；當磁浮列車在上坡道運行時，坡道附加阻力，數值為正，可表示為：

式中：fg為坡道附加阻力，kN；i為坡道的坡度千分值；m為列車總質量，t；g為重力加速度。

綜上所述，磁浮列車在運行時受到的總阻力可用式(5)表示。

式中：Fr為列車在運行時受到的總阻力。

綜上，在運行過程中，將磁浮列車視為單質點模型，并滿足牛頓第二定理，可用式(6)表示。

式中：x為磁浮列車的位移；ν為磁浮列車運行速度；Fp為磁浮列車所受牽引力；Fb為磁浮列車所受制動力；Fr為磁浮列車所受阻力；m為磁浮列車總質量。

在磁浮列車自動運行時，其控制系統中的牽引制動控制器根據目標速度曲線數據、線路信息發送牽引或制動指令，并通過牽引控制系統或制動控制系統使執行器輸出牽引力或制動力，在整個過程中存在一定延時性，建立控制模型如圖2所示。

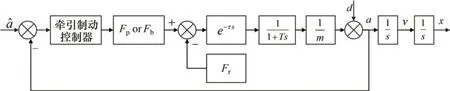
圖2 磁浮列車牽引制動模型框圖Fig. 2 Block diagram of maglev train traction and braking model

1.2 TD-ADRC控制器設計

韓京清[20]提出的自抗擾控制器由跟蹤微分器、非線性狀態誤差反饋控制律和擴張狀態觀測器組成，其控制結構如圖3所示。

圖3 常規2階自抗擾控制框圖Fig. 3 Block diagram of conventional second order active disturbance rejection control

1) 跟蹤微分器

如圖3所示，在常規ADRC中，跟蹤微分器輸出目標曲線(ν)的跟蹤曲線(ν1)和目標曲線的微分(ν2)，其內部函數可設計為式(7)。

式中：函數fhan(x1,x2,r,h0)為最速控制綜合函數[20]，具體表達式見式(8)。ν(k)為跟蹤的輸入，ν1(k)與ν2(k)為跟蹤微分器的輸出，h為積分步長，h0為適當大于h的參數，作用是防止ν1(k)產生超調現象。

式中：r為跟蹤速度因子，r越大，則ν1(k)跟蹤ν(k)的速率越快，精度越高；反之則表示速率更慢、精度更低。

在常規ADRC控制器中，跟蹤微分器的設計有著至關重要的作用，即能夠在一定程度上減小系統輸出的超調量。但是常規ADRC對時滯系統的控制效果不是很好，本文在此基礎上，添加反饋通道和時滯環節，提出TD-ADRC控制器，結構如圖4所示。

圖4 TD-ADRC控制器結構框圖Fig. 4 Block diagram of TD-ADRC

與常規的ADRC控制器中的跟蹤微分器不同的是，TD-ADRC控制器中的跟蹤微分器的輸出只需要目標曲線的微分，如圖4所示，圖中，νˉ為磁浮列車的目標速度曲線，r為跟蹤微分器的輸出，即列車的目標加速度a?，y為系統輸出，即列車的實際加速度a。

2) 擴張狀態觀測器(Extended State Observer，ESO)

擴張狀態觀測器(Extended State Observer，ESO)的作用是由輸出觀測擾動，并將其擴張成為新的狀態變量，此過程不需要分析擾動的具體作用，只需將擾動實時觀測出來從而結合誤差反饋控制律進行消除擾動，控制器的控制效果很大程度上取決于ESO的實時觀測效果。TD-ADRC中的ESO的結構可用式(9)表示。

式中：e為系統的輸出誤差；z1為對系統輸出的觀測估計；z2為對系統總擾動的觀測估計；y為系統的輸出；β1和β2為ESO的可調參數。

3) 誤差反饋控制律

TD-ADRC的實際控制量u可設計成式(10)，虛擬控制量u0可設計成式(11)。

式中：b0為控制器的可調參數。

式中：r為系統輸入，即列車的目標加速度a?；y為系統輸出，即列車的實際加速度a。

2 TD-ADRC調參方法

2.1 模型等效

為了更好地消除磁浮列車具有時滯問題，本文基于式(9)將TD-ADRC結構中的ESO進行分解，得出ESO的傳遞函數如式(12)和式(13)。

式中：Z(s)為ESO的輸出；Y(s)和U1(s)為ESO的輸入。

結合圖4，將式(12)與式(13)代入ESO中，可得出輸入u0至輸出y的傳遞函數，如式(14)所示，對其在低頻域進行近似分析等效，進一步得到近似理想閉環傳遞函數，從而消除時滯環節帶來的系統不穩定性問題，保證磁浮列車速度跟蹤控制系統的穩定性。

在低頻域，對式(14)所示傳函進行近似等效可得：

通過式(15)可以看出，由式(14)得到u0→y的近似傳遞函數可以看作為FOPDT模型(積分環節和時滯環節的乘積)，其中增益記作ka，如式(16)所示。結合圖4，可得控制系統的近似理想閉環傳遞函數如式(17)所示。

對式(17)分母中的時滯環節進行1階泰勒展開得到式(18)，得到理想閉環傳遞函數形式。

2.2 參數調節方法

SKOGESTAD[21]對帶有時滯環節的1階對象的控制進行了研究，分析了PID控制器的參數調節方法，并經過仿真得出當1階系統的時間常數等于時滯環節的時滯時間時，系統具有良好的輸出響應和很好的魯棒性。本文受此啟發，通過調節系統的時間常數和時滯環節的時滯時間的關系來制定參數調節方法。

為了表達簡潔，式(18)中λ可以記作式(19)。

圖5 TD-ADRC參數調整過程Fig. 5 Parameter adjustment process of TD-ADRC

結合式(16)和式(19)，可以得到kp的表達式如式(20)。

當λ=1時，系統的輸出能夠很好地跟蹤輸入[21]。同時，系統擁有良好的魯棒性和抗干擾性，調試過程中，也可在其周圍進行搜索。具體調參方法如下：當給定參數λ時，通過調整參數β1與β2的值，進而確定ka的值，最后確定kp的值，根據系統的輸出特性不斷改變λ的值，以此程序循環。具體算法如圖4所示。

2.3 小結

本章節通過分解ESO，計算出控制系統的開環傳遞函數，并通過低頻域等效的方法將系統的開環傳遞函數等效成FOPDT模型，從而得出理想閉環傳遞函數形式，并據此閉環傳遞函數形式，提出相應的調參策略。該調參策略有以下優點：

1) 簡化了控制系統模型，使手動調參更方便。

2) 計算得出參數間的等量關系，減少了需要整定的參數個數，大大降低了手動調參的難度。

3 仿真分析

結合列車運控模型理論分析，本文設計基于TD-ADRC控制器的磁浮列車速度跟蹤控制系統模型，如圖6所示，包括磁浮列車的牽引(制動)模型、磁浮列車速度響應模型和阻力模型[18]，并在Simulink環境下構建模型如圖7所示，牽引制動模塊如圖8所示。

圖6 磁浮列車速度跟蹤控制系統原理框圖Fig. 6 Principle block diagram of maglev train speed tracking control system

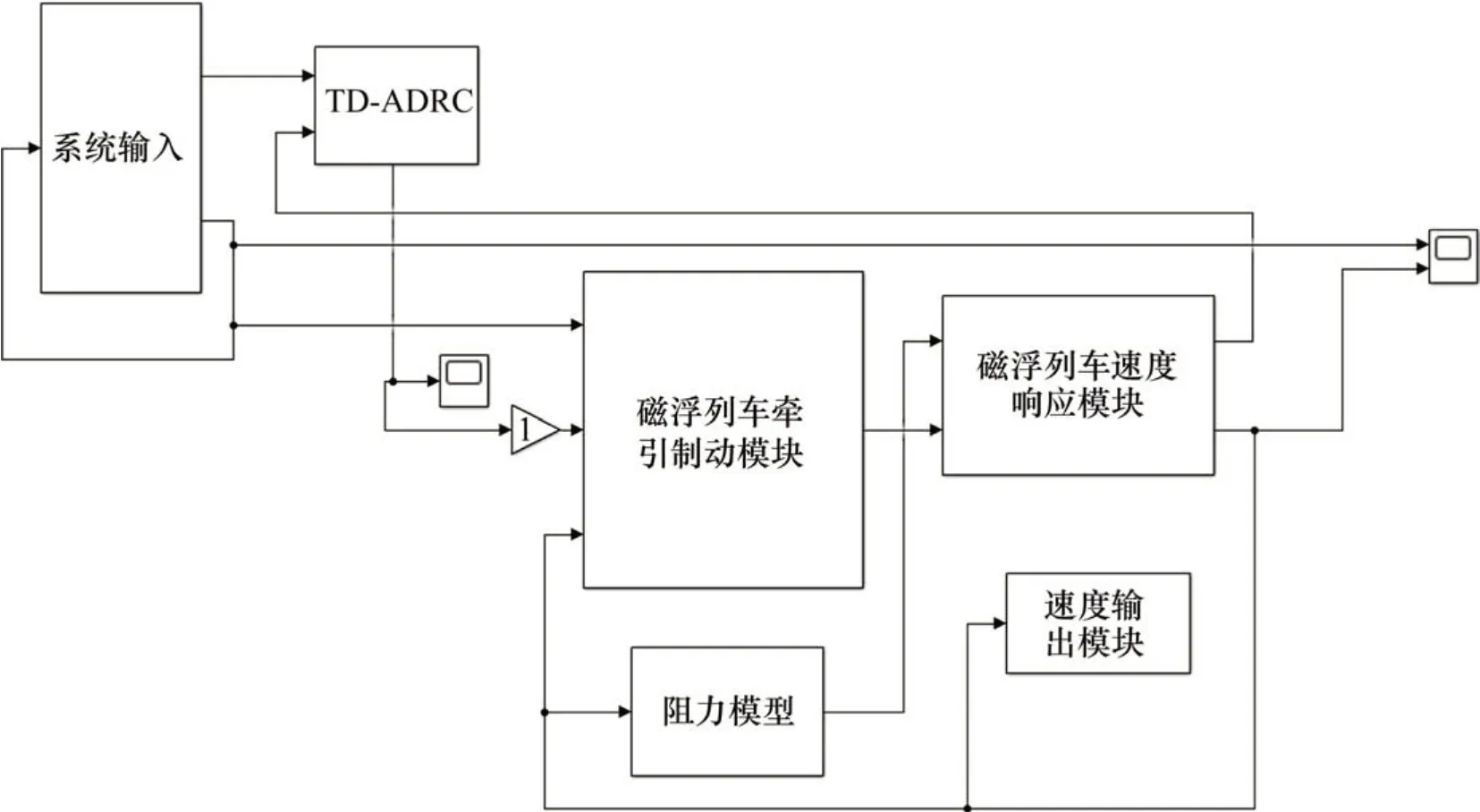
圖7 磁浮列車速度跟蹤控制模型Fig. 7 Speed tracking control model of maglev train

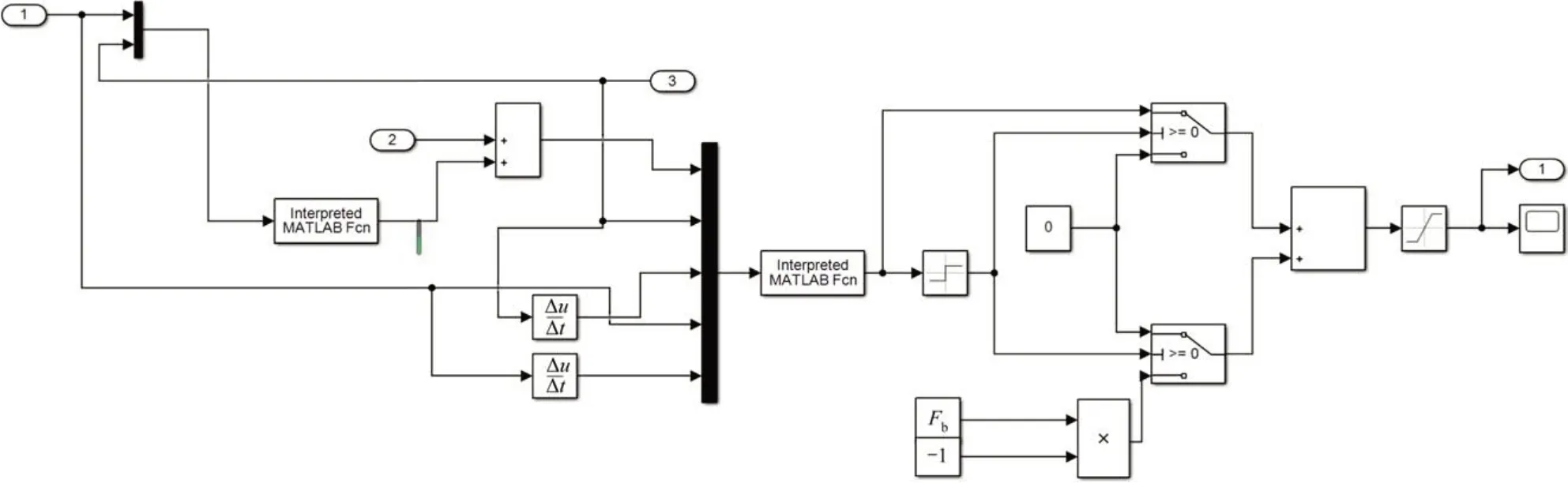
圖8 磁浮列車牽引制動模塊Fig. 8 Traction brake module of maglev train

第一，為了驗證所構建的系統的跟蹤性能，設計系統的輸入信號為10+0.1sin(t)，系統的輸出如圖9所示，誤差如圖10所示。

從圖9和圖10可以看出，整體上，系統的輸出能夠很好地跟蹤目標曲線。細節上，1) 在目標曲線上升段，系統能夠很好地跟蹤正弦輸入信號，誤差較小；2) 而在下降段，系統則會產生相對較大的誤差，但所產生的誤差的數量級均在[-0.005，0.005]范圍之內，表現出良好的跟蹤性能。

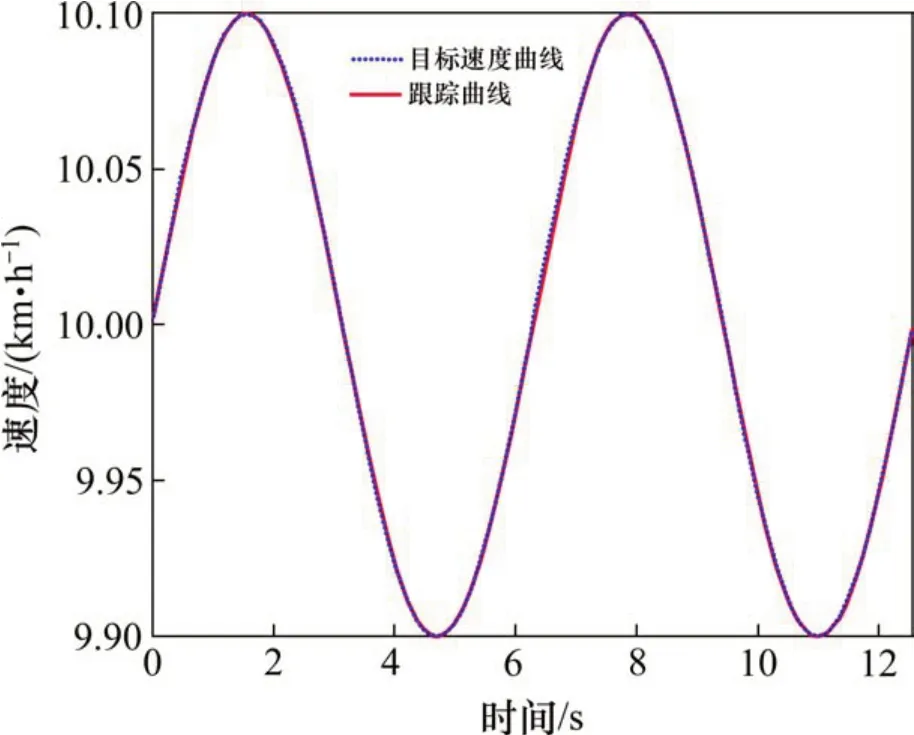
圖9 系統跟蹤正弦信號效果圖Fig. 9 Effect of tracking sinusoidal signal of the system

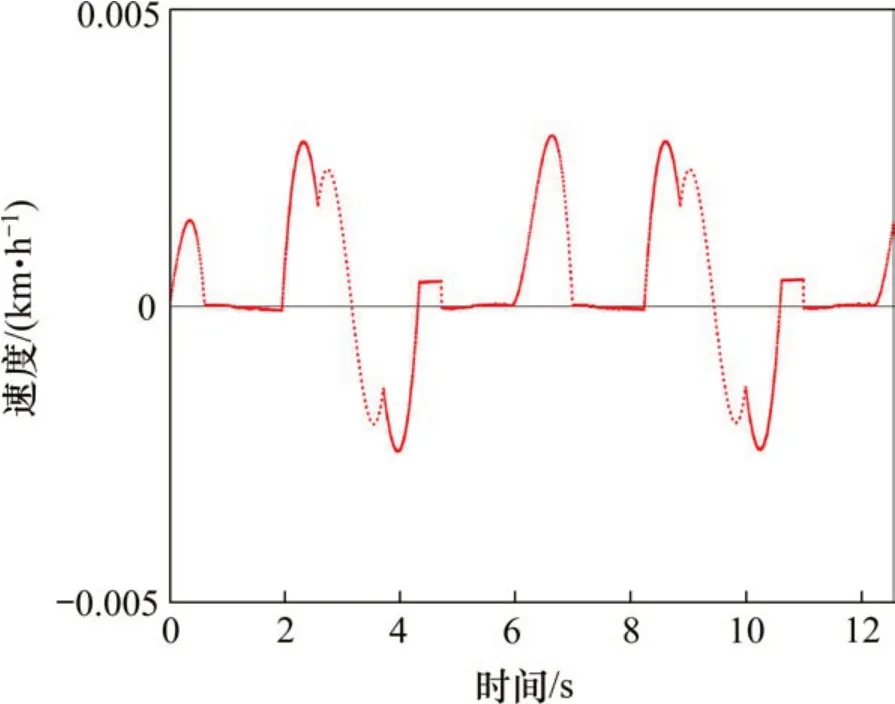
圖10 系統對正弦信號的跟蹤誤差Fig. 10 System tracking error for sinusoidal signal

第二，進一步驗證系統的抗干擾能力，結合圖4，在干擾處添加幅值為0.001的階躍擾動，系統的輸出見圖11。

如圖11所示，在添加擾動后，基于TD-ADRC控制器的系統輸出的最大值最小，且在最短時間內趨于0。這表明，系統在受到控制量處的擾動時能夠通過TD-ADRC控制器很快消除擾動，表現為良好的抗干擾能力。

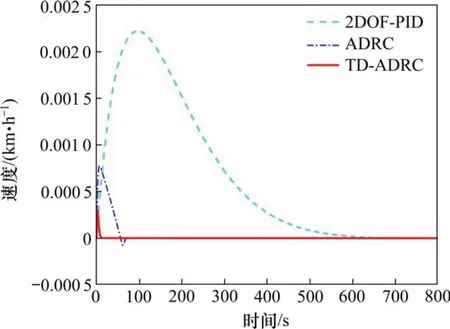
圖11 不同控制器的階躍擾動響應Fig. 11 System step disturbance response based on different controllers

基于圖7的磁浮列車速度跟蹤模型，本文比較了基于2DOF-PID控制器、ADRC控制器、TDADRC控制器的磁浮列車速度跟蹤系統的輸出，3種控制器的速度跟蹤效果如圖12所示。

由圖12分析可知，由于時滯環節的影響，基于2DOF-PID控制器的列車速度跟蹤系統的輸出曲線在加速運行路段與減速運行路段的交界處會出現很大的超調，在減速運行路段和勻速運行路段，跟蹤曲線振蕩幅度較大，當系統受到擾動時，容易陷入不穩定狀態；基于ADRC控制器的列車速度跟蹤系統的輸出曲線在減速運行路段和勻速運行路段出現小幅度的周期振蕩現象；相比于以上2種控制器，基于TD-ADRC控制器的列車速度跟蹤系統在減速運行路段和勻速運行路段都能平穩地跟蹤目標速度曲線，跟蹤精度較高，跟蹤曲線沒有出現振蕩現象，由此可見，TD-ADRC控制器降低了時滯環節給系統帶來的不利影響，保證了系統的穩定性，同時，提高了乘客的舒適感。基于這3種控制器的系統的輸出誤差見圖13。

圖12 基于不同控制器的系統跟蹤效果對比Fig. 12 Comparison of system tracking effects based on different controllers

由圖13知，基于TD-ADRC控制器的磁浮列車速度跟蹤系統的跟蹤誤差最小，其次是ADRC，而基于2DOF-PID的系統輸出誤差最大，直觀體現了TD-ADRC控制器在磁浮列車速度跟蹤控制中的良好性能，這對列車的精準停車有著重要意義。

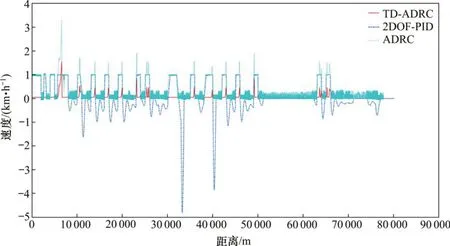
圖13 基于不同控制器的系統跟蹤誤差Fig. 13 System tracking error based on different controllers

4 結論

1) TD-ADRC作為磁浮列車的速度跟蹤控制器，能夠使磁浮列車較平穩無超調地跟蹤目標速度曲線，消除了系統時滯環節引起的速度跟蹤曲線振蕩現象，提高了系統的穩定性，有效降低了系統時滯特性帶來的不利影響，提高了磁浮列車速度跟蹤精度，提高了乘客舒適感。

2) 基于TD-ADRC的磁浮列車速度跟蹤控制系統有良好的抗干擾能力。

該方法在高速列車的速度跟蹤控制、安全性要求很高的化工領域的應用具有良好的參考價值。