作圖法助力物理模型建構,巧解理想氣體變質量問題
胡金朋
(寧夏銀川市寧夏大學附屬中學)
理想氣體變質量問題是高中物理熱學部分的一個難點,也是近年來各省市高考物理考查的熱點.學生對這一問題的理解存在困難的主要原因有兩個:一是理想氣體狀態方程只適用于一定質量的氣體,導致學生在理解變質量氣體問題上存在較大困惑;二是變質量問題情境本身的抽象性導致學生不能正確選擇研究對象,進而無法正確應用理想氣體狀態方程.應用作圖法助力物理模型建構,可以很好地幫助學生理解理想氣體變質量問題.
1 充氣問題
充氣問題要以充氣后密閉容器中的全部氣體為研究對象才能應用理想氣體狀態方程求解,生活中有給籃球、足球和輪胎等充氣情境.
例1一個足球的容積是2.5L,用打氣筒給這個足球打氣,每打一次都把體積為125mL、壓強與大氣壓相同的氣體打進足球內.如果在打氣前足球就已經是球形并且里面的壓強與大氣壓相同,打了20次后足球內部空氣的壓強是大氣壓的多少倍? (假設緩慢進行打氣,過程中氣體溫度不變)
解析
將足球抽象成圖1中的矩形容器,其中已經有體積為V,壓強為p0的空氣,外部還有體積為V0,壓強為p0的20份待充入空氣,它們整體為一定質量的氣體,故可以應用玻意耳定律求解.
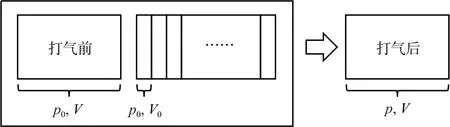
圖1
根據玻意耳定律可得p0(V+20V0)=pV,解得p=2p0.
點評
理解充氣問題是以充氣后的全部氣體為研究對象是解題關鍵,通過作圖建構起研究對象的模型能夠很好地幫助學生理解與應用理想氣體狀態方程.這里也要注意啟發學生思考實際打氣過程溫度是不是不變,引起溫度變化的主要原因是什么.
2 抽(漏)氣問題
抽(漏)氣問題要以抽(漏)氣前密閉容器中的全部氣體為研究對象才能應用理想氣體狀態方程求解,生活中有抽氣拔罐、輪胎漏氣和屋內空氣受熱外溢等情境.
例2(2020年山東卷)中醫拔罐的物理原理是利用玻璃罐內外的氣壓差使罐吸附在人體穴位上,進而治療某些疾病.常見拔罐有兩種,如圖2所示,左側為火罐,下端開口;右側為抽氣拔罐,下端開口,上端留有抽氣閥門.使用火罐時,先加熱罐中氣體,然后迅速按到皮膚上,自然降溫后火罐內部氣壓低于外部大氣壓,使火罐緊緊吸附在皮膚上.抽氣拔罐是先把罐體按在皮膚上,再通過抽氣降低罐內氣體壓強.某次使用火罐時,罐內氣體初始壓強與外部大氣壓相同,溫度為450K,最終降到300K,因皮膚凸起,內部氣體體積變為罐容積的.若換用抽氣拔罐,抽氣后罐內剩余氣體體積變為抽氣拔罐容積的罐內氣壓與火罐降溫后的內部氣壓相同,罐內氣體均可視為理想氣體,忽略抽氣過程中氣體溫度的變化,求應抽出氣體的質量與抽氣前罐內氣體質量的比值.
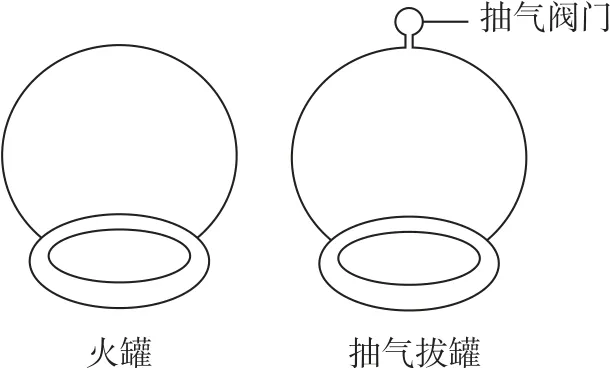
圖2
解析
火罐中為一定質量的氣體,應用理想氣體狀態方程可解出火罐降溫后內部的壓強p2.抽氣罐抽氣過程導致罐內氣體質量發生變化,是變質量問題,要以抽氣前罐內的全部氣體為研究對象.設抽氣前罐內氣體體積為V1,壓強為p1,抽氣降壓后全部氣體體積為V′2,壓強為p2,罐內剩余氣體體積為,被抽出的氣體體積為,如圖3所示.
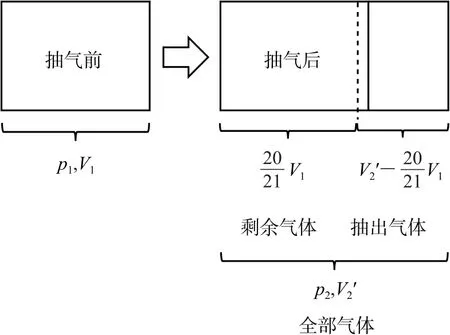
圖3
對火罐,根據理想氣體狀態方程可得
抽氣前罐內氣體的質量和抽氣降壓后全部氣體的質量是相等的,抽氣后全部氣體和被抽出氣體的壓強、溫度都一樣,它們的密度是一樣的,所以應抽出氣體的質量與抽氣前罐內氣體質量的比值為
點評
對抽(漏)氣問題,理解以抽氣前的全部氣體為研究對象是解題關鍵,作圖法能夠有效幫助學生突破思維障礙,從而理解抽氣前后氣體總量是不變的.此題的另一個難點在于抽氣降壓后由于皮膚凸起導致留在罐中的氣體體積不是V1,而是,這一難點通過在圖3中作虛線進行突破,虛線以左的體積表示留在罐中氣體的體積.
3 氣體混合問題
氣體混合問題要以混合前的兩部分氣體各自為研究對象,分別應用理想氣體狀態方程聯立求解,混合后兩部分氣體壓強相等,混合前后體積之和不變.
例3(2020年全國Ⅰ卷)甲、乙兩個儲氣罐儲存有同種氣體(可視為理想氣體).甲罐的容積為V,罐中氣體的壓強為p;乙罐的容積為2V,罐中氣體的壓強為.現通過連接兩罐的細管把甲罐中的部分氣體調配到乙罐中去,兩罐中氣體溫度相同且在調配過程中保持不變,調配后兩罐中氣體的壓強相等.求調配后,
(1)兩罐中氣體的壓強;
(2)甲罐中氣體的質量與甲罐中原有氣體的質量之比.
解析
細管連通前甲罐中氣體壓強大,連通后甲罐中的部分氣體進入乙罐,此過程中甲罐氣壓降低,乙罐氣壓升高,最終兩罐氣壓相等,設為p′.雖然兩罐中氣體混合使得甲罐中氣體質量減少,乙罐中氣體質量增加,但可以分別以甲罐和乙罐中原來的氣體為研究對象,甲罐中原來的氣體在此過程中經歷了等溫膨脹,設膨脹后體積為V1,而乙罐中原來的氣體在此過程中經歷了等溫壓縮,設壓縮后體積為V2,兩罐中氣體混合前后總體積不變,即V1+V2=3V,因此可以分別對甲、乙兩罐中氣體應用玻意耳定律求解,如圖4所示.
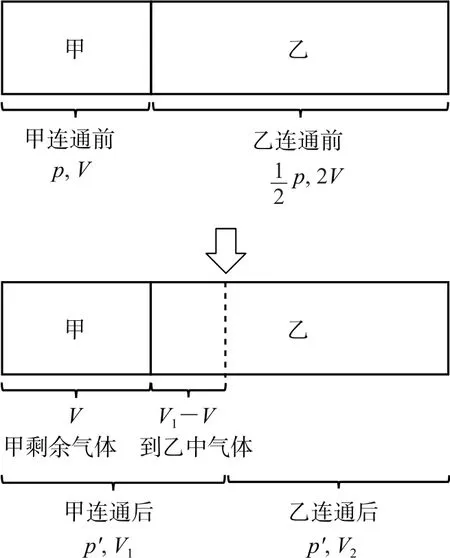
圖4
(1)根據玻意耳定律,對甲罐中原來的氣體有
對乙罐中原來的氣體有
(2)由圖4可知,甲罐中原有氣體質量等于調配后甲罐中剩余氣體質量與到乙罐中氣體質量之和,故調配后甲罐中氣體的質量與甲罐中原有氣體的質量之比為
點評
此題解題關鍵在于以混合前的兩部分氣體各自為研究對象,甲罐中原來的氣體等溫膨脹后體積增大到V1,在圖4中用虛線以左的空間表示;乙罐中原來的氣體等溫膨脹后體積減小到V2,在圖4中用虛線以右的空間表示.作圖法可以幫學生厘清思路,明確研究對象,求解時注意兩部分氣體混合前后總體積不變,混合后壓強相等.
4 氣體分裝問題
氣體分裝問題要以分裝前大容器中的全部氣體為研究對象,應用理想氣體狀態方程求解,注意分裝結束時大容器中還剩余一部分氣體,這些氣體不會被分裝到小容器中,但也是全部氣體的一部分.
例4(2016 年全國Ⅱ卷)一氧氣瓶的容積為0.08m3,開始時瓶中氧氣的壓強為20個大氣壓.某實驗室每天消耗1個大氣壓的氧氣0.36 m3,當氧氣瓶中的壓強降低到2個大氣壓時,需重新充氣.若氧氣的溫度保持不變,求這瓶氧氣重新充氣前可供該實驗室使用多少天.
解析
設實驗室每天消耗氧氣的壓強為p0、體積為V0,分裝前氧氣瓶中氣體壓強為p、體積為V,當氧氣瓶中氣壓降低到2個大氣壓時,其內部剩余氣體不會被分裝,設此時壓強為p1.如圖5所示,用作圖法表示出氧氣瓶中的全部氣體等溫膨脹至壓強為p1、體積為V1的情形,其中體積為V的部分氣體會留在氧氣瓶中,而體積為V1-V的氣體是即將被分裝的氣體.由于最終實驗室每天消耗的是1個大氣壓的氧氣,因此再用作圖法表示出這部分壓強為p1、體積為V1-V的氣體等溫膨脹至壓強為p0、體積為V2的情形,最終求出體積V2與實驗室每天消耗氧氣的體積V0的比值,即為使用天數.
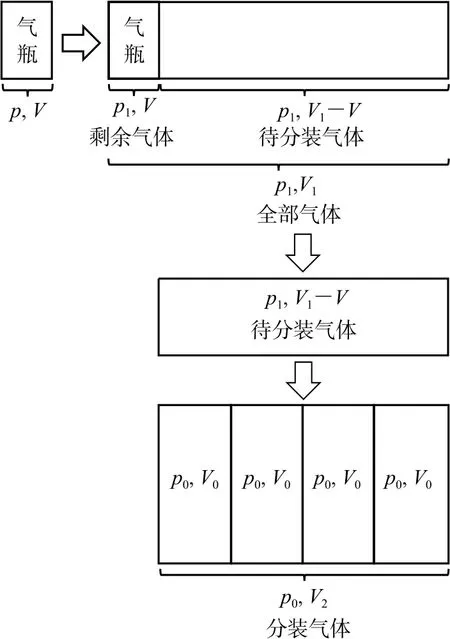
圖5
對氧氣瓶中的全部氣體壓強由p變為p1的過程應用玻意耳定律得pV=p1V1,解得V1=0.8 m3;則待分裝氣體的體積為V1-V=0.72m3.
對待分裝氣體壓強由p1變為p0的過程應用玻意耳定律得p1(V1-V)=p0V2,解得V2=1.44 m3;則在氧氣瓶重新充氣前可供實驗室使用的天數為
點評
此題先以氧氣瓶中的原有氣體為研究對象,應用玻意耳定律解出氣體壓強變為2個大氣壓時的體積,然后以待分裝氣體為新的研究對象,應用玻意耳定律解出待分裝氣體壓強變為1個大氣壓時的體積,最后求出使用天數.應用作圖法可以有效幫助學生分清楚第一個過程的研究對象和第二個過程的研究對象是不同的,同時也能夠有效啟發學生理解留在氧氣瓶中的氣體不能被分裝的難點.

(完)

