機械波的多解問題解法揭秘

劉 丁

(寧夏銀川一中)

機械波的多解是機械波一章的難點,是高考的重要考點,也是很多學生在學習過程中過不去的坎.下面就機械波的多解問題進行分析.造成波動問題多解的主要原因有以下幾種.

1 周期性

1)時間周期性:時間間隔Δt與周期T的關系不明確造成多解.2)空間周期性:波傳播距離Δx與波長λ的關系不明確造成多解.

2 雙向性

1)傳播方向雙向性:波的傳播方向不確定.

2)振動方向雙向性:質點振動方向不確定.

由于雙向性造成的多解需注意如下幾種情況.

a)質點到達最大位移處,則有正向和負向最大位移兩種可能.

b)質點由平衡位置開始振動,則起振方向有向上、向下(或向左、向右)兩種可能.

c)只告訴波速不指明波的傳播方向,應考慮沿兩個方向傳播的可能,即沿x軸正方向或沿x軸負方向.

d)只給出兩時刻的波形,則有多次重復出現的可能等.

解決此類問題時,往往采用從特殊到一般的思維方法,即找到一個周期內滿足條件的特例,在此基礎上進行解答.如知時間關系,則加nT;如知空間關系,則加nλ.

3 隱含性

在波動問題中,往往只給出完整波形的一部分,或給出幾個特殊點,而其余信息均處于隱含狀態.這樣,波形就有多種情況,形成波動問題的多解性.

4 典例分析

例1(2021年遼寧卷)一列沿x軸負方向傳播的簡諧橫波,t＝2s時的波形如圖1-甲所示,x＝2m處質點的振動圖像如圖1-乙所示,則波速可能是( ).

圖1

解析

根據圖1-乙,可知t＝2s時x＝2m 處的質點正經過平衡位置向下振動;又因為該波向負方向傳播,結合圖1-甲可知x＝2m 為半波長的奇數倍,即有

而由圖乙可知該波的周期為T＝4s,所以該波的波速為

例2(2021年海南卷)一列沿x軸正方向傳播的簡諧橫波,其波源的平衡位置在坐標原點,波源在0～4s內的振動圖像如圖2-甲所示,已知波的傳播速度為0.5m·s－1.

圖2

(1)求這列橫波的波長;

(2)求波源在4s內通過的路程;

(3)在圖乙中畫出t＝4s時刻的波形圖.

解析

(1)由題知圖甲為波源的振動圖像,則可知A＝4cm,T＝4s,又由于波的傳播速度為0.5m·s－1,根據波長與速度關系有λ＝vT＝2m.

(2)由(1)可知波源的振動周期為4s,則4s內波源通過的路程為s＝4A＝16cm.

(3)由題圖可知在t＝0時波源的起振方向向上,由于波速為0.5 m·s－1,則在4s時,根據x＝vt＝2m,可知該波剛好傳到位置為2m 的質點,且波源剛好回到平衡位置,且該波沿正方向傳播,可繪制出t＝4s時刻的波形圖如圖3所示,本題明確了波的傳播方向,所以未產生多解.

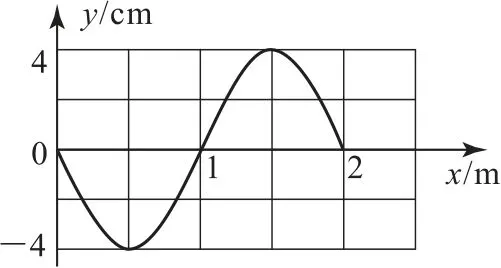
圖3

例3(2021年全國乙卷)圖4中實線為一列簡諧橫波在某一時刻的波形曲線,經過0.3s后,其波形曲線如圖4 中虛線所示.已知該波的周期T大于0.3s,若波是沿x軸正方向傳播的,則該波的速度大小為_________m·s－1,周期為_________s,若波是沿x軸負方向傳播的,該波的周期為_________s.

圖4

解析

因為T＞0.3s,所以該波經過0.3s后傳播的距離不是一個波長,不存在周期性多解.若波是沿x軸正方向傳播的,波形移動了15cm,由此可求出波速和周期,即

若波是沿x軸負方向傳播的,波形移動了5cm,由此可求出波速和周期

例4(2021年山東卷)一列簡諧橫波沿x軸傳播,如圖5所示,實線為t1＝2s時的波形圖,虛線為t2＝5s時的波形圖.以下關于平衡位置在O處質點的振動圖像,可能正確的是( ).

圖5

解析

機械波的傳播方向不確定,所以需要考慮機械波沿x軸正向和負向傳播.

若機械波沿x軸正方向傳播,在t1＝2s時O點振動方向豎直向上,傳播時間Δt＝t2－t1＝3s,滿足

機械波的多解問題產生的根本原因是機械波的周期性重復,在求解該類問題時,要充分重視圖像的功能,對圖像進行仔細分析,挖掘隱含條件,結合傳播方向,利用波動知識,把波動問題全面圓滿地解決.

(完)