無限脈沖響應切比雪夫數字帶通濾波器的設計
何穎,安曉莉
(西安思源學院 電子信息工程學院,陜西西安, 710038)
0 引言
數字信號的處理在最近的幾年中發展迅速,是最有前景的學科之一。數字信號處理是指的將連續的模擬信號經過采樣和模數轉化,成為數字信號,輸入到計算機中進行處理,在數字信號處理的內容中,信號濾波是最重要的一個環節。對信號進行濾波是現在的各種電子信息產品所必備的,濾除掉不要的或者說干擾的頻率信號留下需要的頻率信號[1~2]。
對數字信號進行濾波引起了國內外專家學者的廣泛關注,數字濾波器的設計工作在世界范圍內的研究如火如荼地進行中。由于數字信號濾波器具有眾多的優點,如:可靠性高、準確性高、靈活性高等,從而被廣泛地應用于各行各業。隨著信息時代的進一步發展,數字信號濾波的需求和要求也是不斷提高,數字濾波器的分析和設計變得更為重要[3~5]。
利用MATLAB進行數字濾波器的設計和分析可以更為方便地為實際的濾波器的設計提供思路和想法。能夠極大地縮短濾波器研發和設計所用的時間,并能夠獲得更高的設計性能。
無限長脈沖響應(IIR)數字帶通濾波器設計時,首先給定數字濾波器的性能指標,然后按照頻帶變換轉換成相應的模擬濾波器的性能指標,進行模擬濾波器的響應設計,最后根據雙線性變換原則將模擬濾波器變換成數字濾波器。
1 傅里葉變換
傅里葉變換是建立以時間為自變量的“信號”與以頻率為自變量的“頻譜函數”之間的某種變換關系。性能指標變換規則有沖激響應不變法、階躍響應不變法、雙線性變換法等。雙線性變換法可以較準確地控制截止頻率的位置,克服了產生頻率響應的混疊失真,穩定的模擬濾波器經雙線性變換后所得的數字濾波器必定穩定,雙線性變換法為了克服多值映射,首先把整個s平面壓縮變換到某一中介的s1平面的一條橫帶中,變換關系為即得再通過變換z=es1T把橫帶映射到z平面上,實現了s平面與z平面的一一對應關系。
2 切比雪夫低通濾波器
切比雪夫濾波器是一種在通帶中等波紋、阻帶中單調的濾波器,稱為切比雪夫Ⅰ型[6~8]。其低通濾波器幅度響應為:
式中,ε為小于1的正數,表示通帶波紋大小的一個參數,ε越大,波紋也越大。N代表濾波器的階次,
3 離散周期序列的傅里葉級數(DFS)
給定信號為:
x(t) = 30sin(2π?10 ?t) + 30sin(2π? 2000 ?t) + 30sin(2π? 6000 ?t)
(1)求x(t)的傅里葉變換:
可先將x(t)其展成指數型,對比FS反變換公式:x(t)=求出傅里葉級數的系數X(jk?0)。對x(t)采樣得x(n),求:
因篇幅有限,7200個點圖像過于密集,圖1只給出X~(k)在k=?6 50,… , 0,… , 650區間的頻率特性。可看出,圖形關于原點共軛偶對稱,即幅頻特性為偶函數,相頻特性為奇函數。事實上,在k= 0,1,… , 7199周期里,有
可得X~(k)的頻率特性如圖1所示。k= 1,200,600,6600,7000,7199幅值為108000,并且相頻特性關于(3599.5,0)對稱。
2)將電熔套管從包裝袋中取出,并檢查確認配件內壁是干凈的。如有需要,可使用酒精擦拭紙擦拭電熔套管內壁,在開始焊接工藝前,確保清潔后的電熔套管內壁是完全干燥。
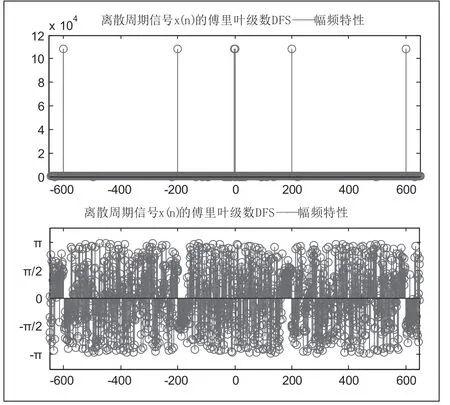
圖1 的頻率特性
4 切比雪夫濾波器運算設計
■4.1 模擬帶通濾波器
①求ε和N。
取N為最小正整數N=2。
②求3dB截止頻率?3dB。
把N=2代入到阻帶指標要求公式中,阻帶指標滿足要求,且由于N= 2 > 1.7747,因而通帶指標一定超過要求。將N=2代入阻帶條件,可得:
歸一化參數:
③查表法求解切比雪夫低通濾波器G(p)。
根據N=2,查表可得歸一化原型濾波器,
④模擬低通到模擬帶通的轉換。
根據題目要求,分母整理為常1多項式,即分子分母同時除以 2.4812×1016,可得H(s)。
■4.2 數字帶通濾波器
根據題目要求,分母整理為常1多項式,即分子分母同時除以20
4.3983×10 ,可得:
將系統函數系數代入表1,即可得到IIR帶通濾波器的直接Ⅱ型結構。
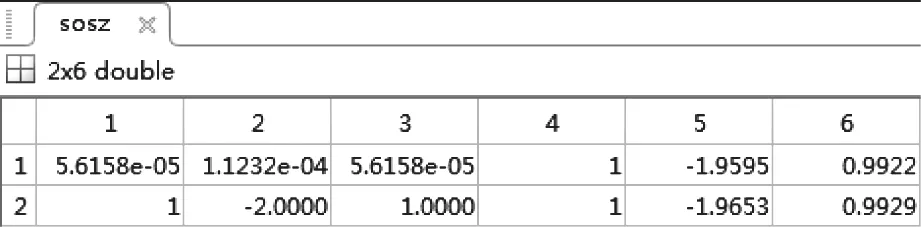
表1 IIR帶通濾波器的直接Ⅱ型結構
5 實驗及結果分析
■5.1 模擬濾波器分析
圖2、圖3,分別從時域和頻域對切比雪夫模擬帶通濾波器進行分析,濾波器滿足題目要求的各項性能指標,且具有良好的穩定性、快速性和準確性。
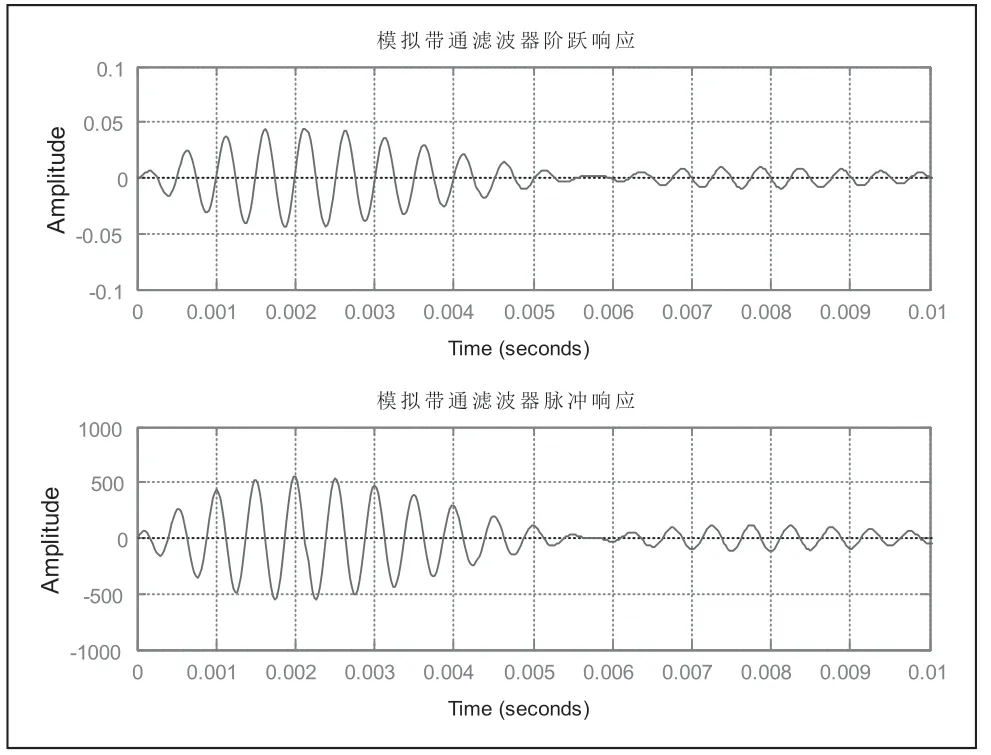
圖2 切比雪夫模擬帶通濾波器階躍響應和脈沖響應
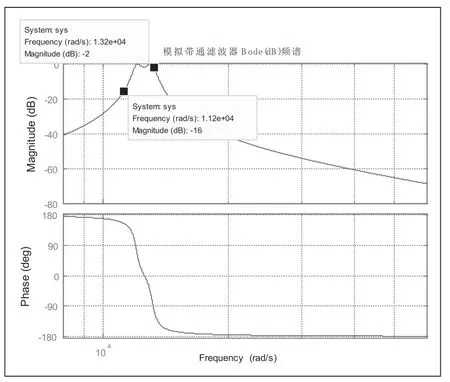
圖3 切比雪夫模擬帶通濾波器頻譜圖
從圖3中,幅頻圖中可以明顯看到切比雪夫濾波器最大的特點:波紋特性,從相頻圖中可以看到其最大的優點,相比巴特沃斯濾波器,頻率響應曲線之間的誤差最小。由于該波紋的谷值接近要求的通帶衰減,導致該參數下切比雪夫濾波器幅值失真。如圖4、圖5,將切比雪夫模擬帶通濾波器的輸入和輸出進行對比,發現輸出函數的幅值不是2000Hz分量的幅值30,而僅為24。圖5中給出當輸出波形尚未穩定時與輸入信號2000Hz分量幾乎重合,這意味著在該暫態過程中濾波器濾去了低頻和高頻諧波。而穩態后,相位沒有偏差,僅在幅值上存在一定差值。可以通過校正,以增益系數來改變切比雪夫濾波器。
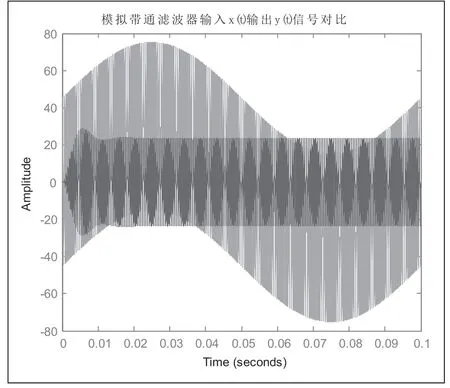
圖4 切比雪夫模擬帶通濾波器輸入輸出信號對比
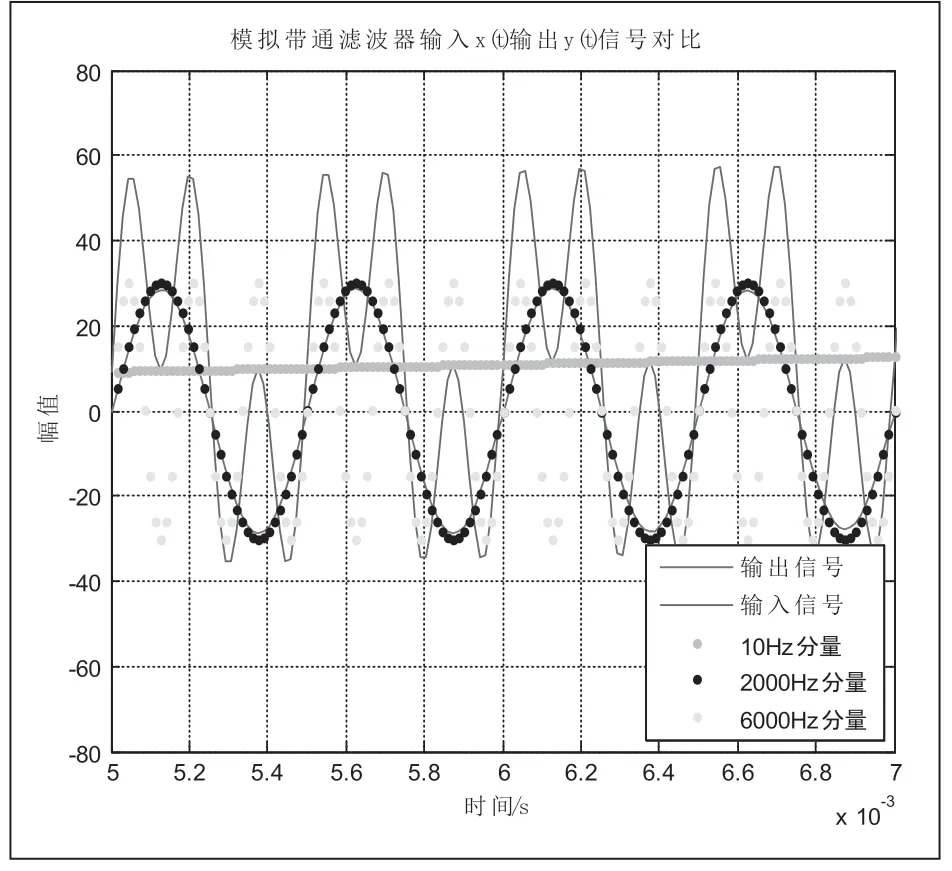
圖5 切比雪夫模擬帶通濾波器輸入及各分量與輸出信號的對比
■5.2 數字濾波器分析
圖6、圖7分別從時域和頻域對切比雪夫數字帶通濾波器進行分析,濾波器滿足題目要求的各項性能指標。圖6中,其穩定性、快速性和準確性看起來相對巴特沃斯波動次數較多。
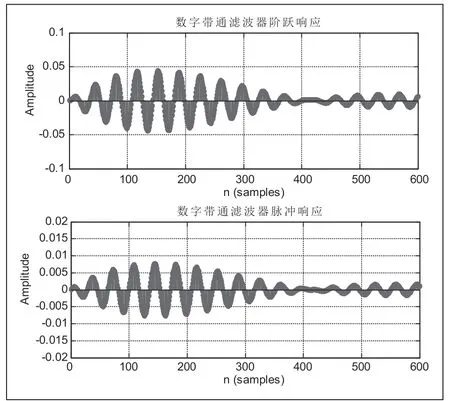
圖6 切比雪夫數字帶通濾波器階躍響應和脈沖響應
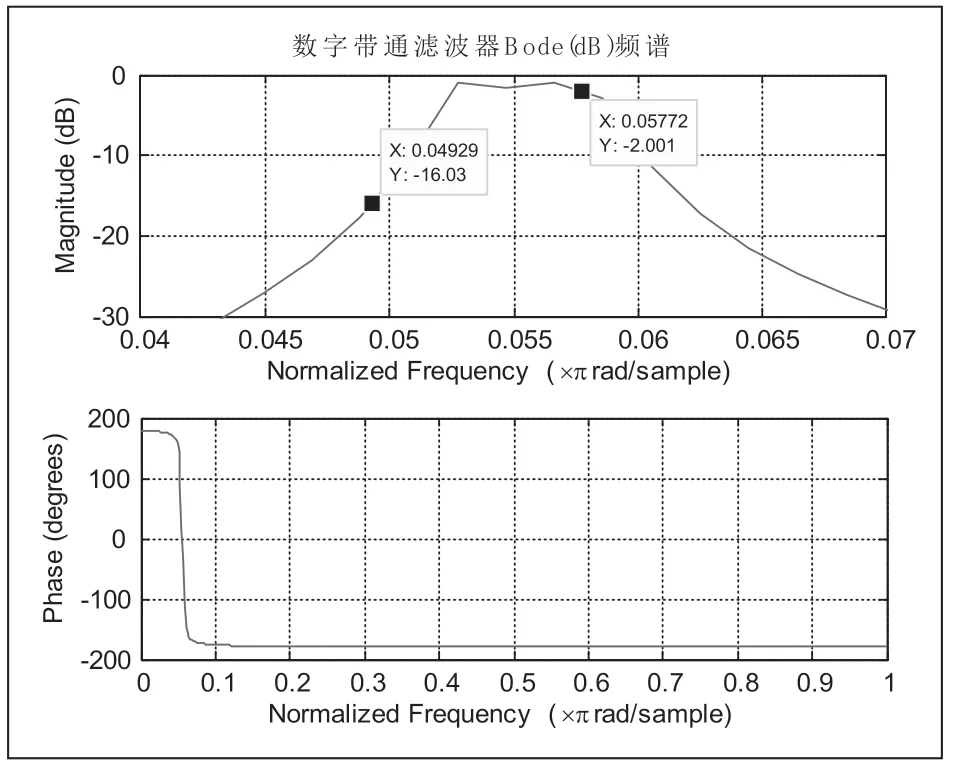
圖7 切比雪夫數字帶通濾波器的頻譜圖
圖8將切比雪夫數字帶通濾波器的輸入和輸出進行對比。相比最平的巴特沃斯濾波器,存在一定的幅度失真。

圖8 切比雪夫數字帶通濾波器輸入及各分量與輸出信號的對比
圖9給出了切比雪夫數字帶通濾波器輸出信號的頻譜圖,可見圖1所示抽樣信號經過濾波器之后,只剩下2000Hz頻率,滿足題目要求。說明切比雪夫帶通濾波器之后,相位沒有發生失真,僅僅有幅值不滿足要求,故采用增益校正可行。
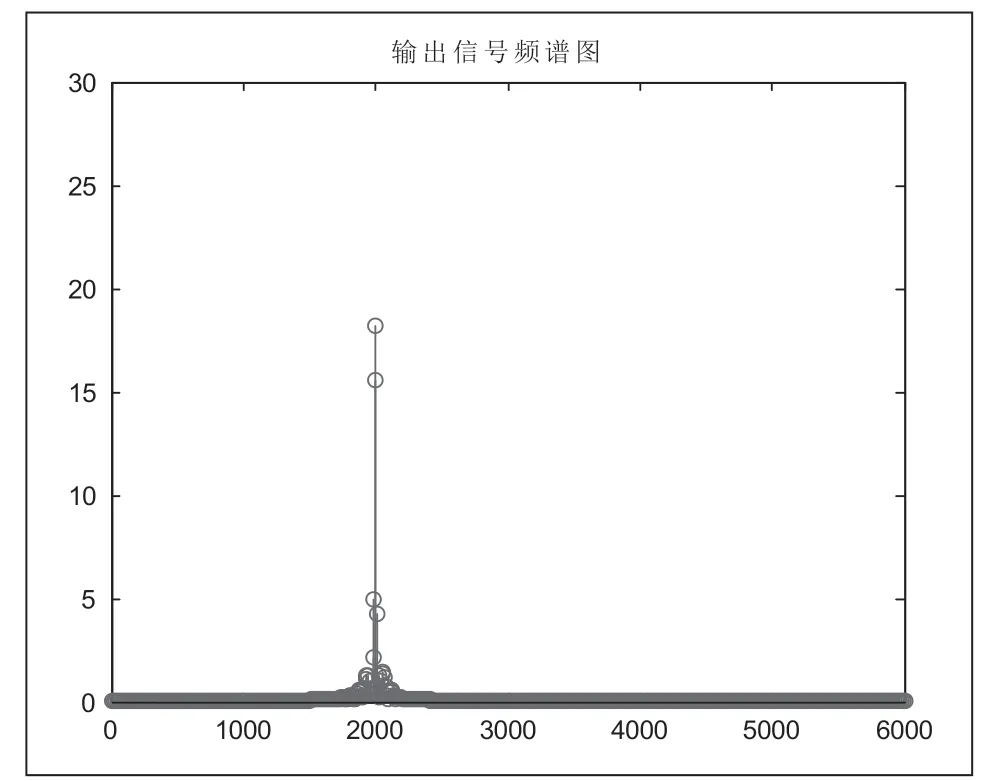
圖9 切比雪夫數字帶通濾波器輸出信號頻譜圖
6 結論
切比雪夫濾波器在過渡帶比巴特沃斯濾波器的衰減快,其經濟性會更好,但頻率響應的幅頻特性不如后者平坦。切比雪夫濾波器和理想濾波器的頻率響應曲線之間的誤差最小。就其輸出效果而言,在相同指標下,切比雪夫濾波器的階次較小,但對于帶通濾波器而言,由于切比雪夫Ⅰ型濾波器在通頻帶內存在幅度波動。

