雙碳目標下考慮風光不確定性的綜合能源系統規劃研究

徐 楠，趙子豪，張丹陽，周 波，王永利，聶 婧，宋 妍

（1.國網河北省電力有限公司經濟技術研究院，河北 石家莊 050000；2.華北電力大學 經濟與管理學院，北 京 102206）

0 引言

“雙碳”目標促進了全社會加快調整優化產業結構、能源結構。綜合能源系統（IES）能夠充分消納可再生能源，解決其不確定性，進而有效的增加綜合能源系統的工作效率，降低碳排放，具有廣闊的發展前景。

現有的綜合能源系統規劃模型多以經濟性為目標，輔以可靠性和環保型等目標，對設備的容量進行優化配置。文獻[1]利用場景法描述光伏不確定性，并運用基于Wasserstein概率距離的場景削減0-1規劃模型，對大量不確定性場景進行削減，并采用基于場景分析法的兩階段規劃策略對此模型進行求解，得到含整數變量的多能源容量規劃方案。文獻[2]中的上層規劃模型以系統年凈成本和綜合缺能率最小為目標；下層優化運行模型將上層模型確定的配置方案轉換為線性約束條件，以系統切負荷量最低和運行經濟性最優為目標，實現系統的優化運行，建立了區域綜合能源系統規劃與運行相結合的雙層多目標優化配置模型。文獻[3]面向園區級綜合能源系統，對影響規劃的內外部主要因素進行定量分析，提出一種以園區綜合能源系統全壽命周期等值年成本為目標的優化配置方法。文獻[4]按照負荷特性的不同，將規劃區域分為不同的區域，建立以冷熱電聯產系 統 （Combined Cooling Heating and Power，CCHP）為主的規劃模型，得到不同區域內的設備容量，實現多類型多區域綜合能源系統協同規劃。文獻[5]建立考慮節點流量平衡、熱能—流量約束及熱損平衡約束的熱網模型，結合CCHP系統能量平衡約束和熱網模型，建立了多區域CCHP系統容量協同優化配置的混合整數線性規劃模型。

IES主要以大規模可再生能源作為一次能源，在保證系統可再生能源消納能力情況下，對可再生能源不確定性的分析和處理成為優化規劃中的關鍵問題。文獻[6]分析了系統接入高比例可再生能源后，系統的靈活性，但側重從規劃層面加以分析，日前調度計劃中可再生能源的消納電量未知。文獻[7]，[8]根據風/光出力與電/熱負荷的不確定性分析，以條件風險價值理論為基礎，合理構建綜合能源系統的經濟調度模型，探究在綜合能源系統運行過程中可能出現的成本增加風險。文獻[9]應用概率相關性質對約束條件進行描述，形成以機會約束規劃為基礎的數學模型，其中包含風電場的電力系統與經濟相關調度。文獻[10]通過對風速的預測，構建風速預測可能誤差概率模型，同時，使用隨機規劃理論的概率約束模型來合理規劃和考慮與電力系統（包括風電場）的動態經濟調度有關的問題。文獻[11]，[12]考慮到光伏與風電在加入電力系統后，會對其旋轉備用容量產生影響，所以在實際測算中，需要應用序列運算方法解決風電、光伏和負荷的不確定性問題，同時還需要利用目標函數將結果轉化為相應數據統計，進而達到優化機組的出力計劃和旋轉備用容量的目的。文獻[13]提出了一種指數標度優化層次評價方法，同時對于多種常見的風電消納的使用方法從社會經濟效益的角度做出分析。

本文根據風光能源出力的不確定性，構建IES規劃優化模型，耦合了冷、熱、電等多種能源形式，通過各類設備的協調運行來滿足終端用戶的用能需求，對可再生能源消納有良好的效果，不僅改善了系統負荷水平且具有更好的經濟效益。

1 綜合能源系統模型

為了消納高比例風光可再生能源，系統需要具有足夠的調節能力。通過能量樞紐的耦合轉化，終端用戶的冷熱電需求可由多種形式滿足。本文的綜合能源系統能量流如圖1所示。

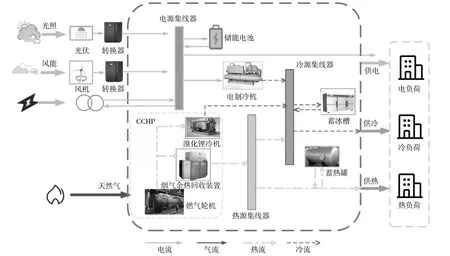
圖1 綜合能源系統典型結構Fig.1 Integrated energy system energy flow

圖中電能子系統主要由風機、光伏、CCHP、儲能電池等部分構成，儲能電池可用于平抑風電、光伏等可再生能源的出力波動，即在可再生能源出力大于消納空間時，可通過電儲能直接儲存，進而提升了整個系統用電的靈活性，提高了可再生能源消納水平。

2 風光出力不確定性處理

為了充分利用可再生能源，IES須具有較強的調節能力，因此，系統會配備一定的儲能裝置以及能源裝換裝置，這些裝置可以極大的提高系統用電靈活性，并且加大了風電、光伏等可再生能源的消納能力。

2.1 光伏出力特性分析

太陽光照強度的分布規律符合Beta分布特征，其概率密度函數為

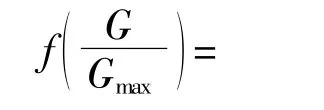
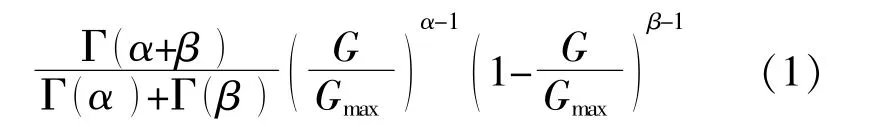
式中：G為本時段里實際的光照強度，kW/m2；Gmax為本時段內的最大光照強度，kW/m2；α，β分別為Beta分布的兩個形狀參數，這些參數受到光照強度的平均值和標準差等因素的影響。

光伏組件的功率為

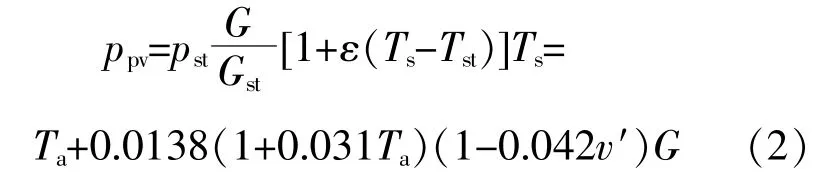
式中：ppv為光伏組件實際輸出功率；pst為標準測試條件下光伏組件最大輸出功率；Gst為標準條件下光照強度；ε為光伏功率溫度系數；Ts為光伏電池的表面溫度，℃；Tst為標準條件下光伏電池表面溫 度，設 定 為25℃；Ta為 環 境 溫 度；v′為 風 速。

2.2 風機出力特性分析

風速的變化符合Weibull分布，即：

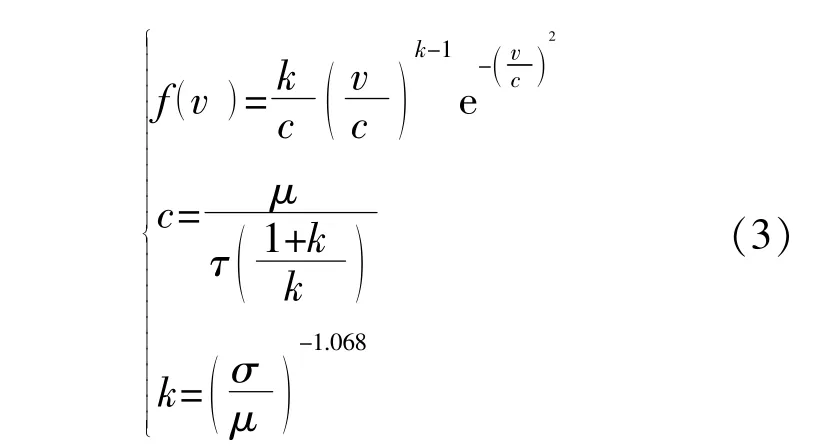
式中：c，k分別為Weibull分布的尺度參數和形狀參數（二者均大于0）；σ，μ分別為其標準差和期望；v為風速。

結合風速模型，可得風機出力的數學模型為

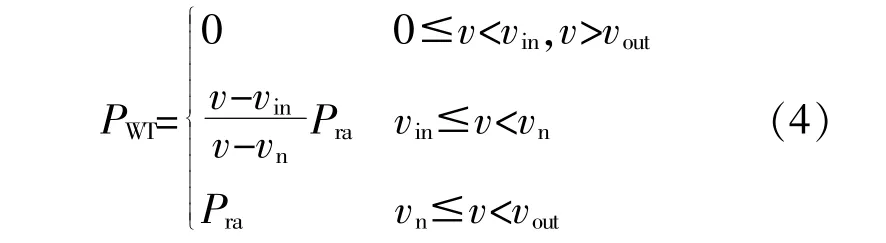
式中：PWT，Pra分別為風機出力的有功出力和額定出 力；vin，vout，vn分 別 為 風 機 的 切 入、切 出 和 額 定 風速。

2.3 風光出力的區間數轉換

通過對風光設備出力的多次預測可以獲得其在各個時段內的預測均值和方差，進而t時段的設備出力區間的上、下限為

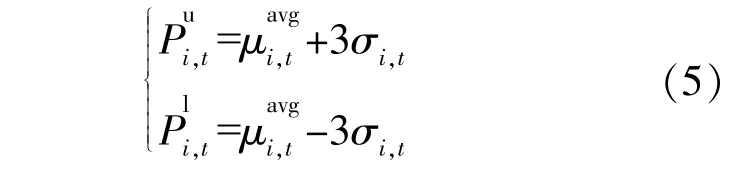
3 考慮風電、光伏出力不確定性的IES規劃優化模型

3.1 目標函數

本文所建立的規劃模型的優化目標包括系統經濟性和環境性雙重目標。

（1）經濟性目標

經濟優化目標包括投資成本、電網購電成本和設備運行維護成本。

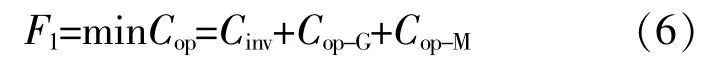
式中：Cop為系統運行成本；Cinv為年化投資費用；Cop-G為購電成本；Cop-M為設備運行維護成本。

①電網購電成本

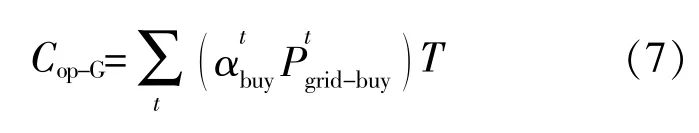
②設備運行維護成本

式中：Ci為分布式發電的運行維護成本；Pi為分布式發電的輸出功率，kW。

（2）環境性目標

綜合能源系統的環境成本分為能源生產過程中產生的污染物造成的環境損失和由此造成的非環境損失兩方面，有關部門收取的排污費。環境成本最小化模型為

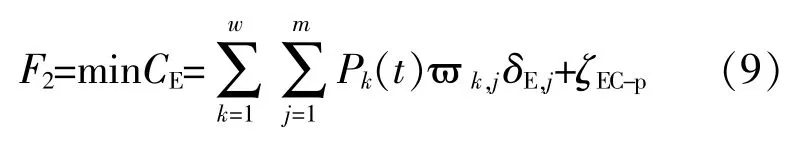
式 中：CE為 環 境 成 本；Pk（t）為t時 刻 的 排 放 源k的功 率；?k，j為 來 自 排 放 源Pk（t）的 污 染 物 的 排 放 系數；δE，j為 污 染 物 的 單 位 成 本；ζEC-p為 污 染 物 排 放懲罰費用。

3.2 約束條件

（1）能源平衡約束

①電功率平衡約束

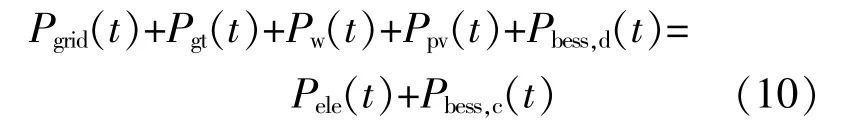
式中：Pgrid（t）為綜合能源系統和電網之間t時刻的交 互 功 率；Pgt（t）為 燃 氣 輪 機t時 刻 的 出 力；Ppv（t）為 光 伏 在t時 刻 的 出 力；Pbess，d（t）為 蓄 電 池 在t時刻 的 放 電 功 率；Pele（t），Pbess，c（t）分 別 為 系 統 內t時刻的電負荷、蓄電池的充電功率。

②熱功率平衡約束

在熱力傳輸的過程中，會變現出一定的延遲特性。此外，由于在供熱舒適度方面也存在不同程度的模糊性，所以實際供熱需求并不需要滿足熱能平衡的實時平衡，只需要保證熱能在一定程度下滿足相應指標，可以在一定程度上出現供需不平衡的狀態。需要滿足的約束條件為

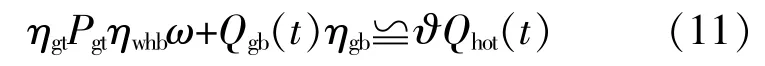
式中：ηgt為燃氣輪機的產熱效率；ηwhb為余熱鍋爐的產熱效率；ω為熱分配系數，用以分配供給制冷機和制熱水的熱量；Qgb（t）為燃機鍋爐在t時刻的出 力；Qhot（t）為 系 統 內t時 刻 的 熱 負 荷；?為 熱 負荷的調節系數。

③冷功率平衡約束

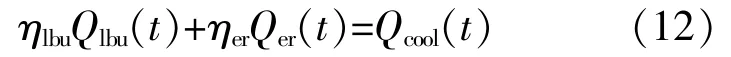
式 中：ηlbu為 溴 化 鋰 制 冷 機 的 制 冷 效 率；Qlbu（t）為 溴化鋰制冷機在t時刻的制冷功率；ηer為電制冷機的制冷效率；Qer（t）為電制冷機在t時刻的制冷功率；Qcool（t）為 系 統 內t時 刻 的 冷 負 荷。

（2）能源供應約束

在區域綜合能源系統中，考慮到系統和外部的交互關系以及系統與能源網的安全，在系統與外部網絡兩者之間進行能量交換時，其交換功率要限定在一定范圍內，即：

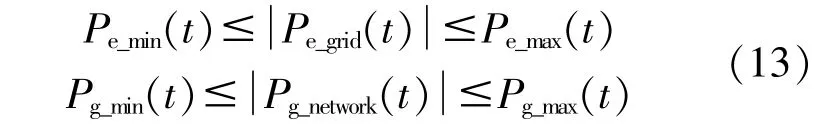
式中：Pe_min（t）為電網與綜合能源系統之間的最小功率交換；Pe_max（t）為電網與綜合能源系統之間的最大電量交換功率；Pg_max（t）為天然氣網向系統供應天然氣的最大功率；Pg_min（t）為天然氣網向系統供應天然氣的最小功率。

3.3 不確定性問題魯棒優化確定化處理

針對風電和光伏發電的不確定性，本文采用魯棒優化模型進行標準化處理。魯棒優化的一般模型可以描述為

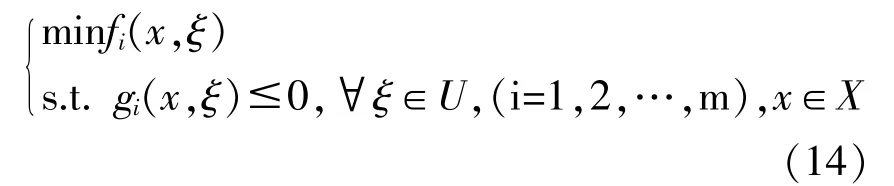
式中：fi為第i個目標函數；x為決策變量；ξ為不確定性系數；gi為第i個約束條件；U為不確定性系數的集合。

魯棒優化模型可以滿足不確定性集合中所有不確定性的情況，因此也可以滿足最大不確定性的狀態，從而將不確定性約束條件變換為

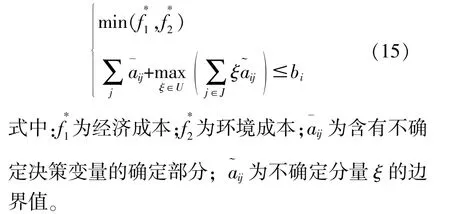
采用對偶錐的方法對模型再次轉換，將表示為 ∞范數錐，則約束條件可轉換為

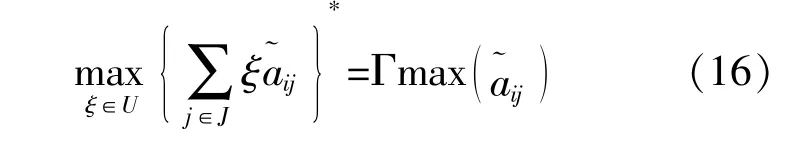
式中：Γ為總不確定度。

針對風電、光電出力的不確定性，通過上述轉化方法對約束條件進行魯棒轉換，最終得到確定性多目標優化問題進行求解。

3.4 求解算法

本文設定經濟性和環境性兩個優化目標，采用粒子群算法求解。本文采用的規劃方法關鍵在于降低風光不確定性的影響，增加風光的消納能力，在實際工程中具有比較廣泛的應用，具體的求解流程如圖2所示。

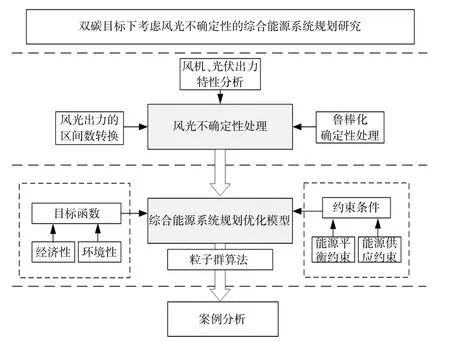
圖2 求解基本流程Fig.2 The basic process

4 案例分析

本文案例選取吉林省某園區進行驗證。園區全年熱負荷波動較大，其中冬季較為寒冷，最大熱負荷整體為0～500kW，最大冷負荷為350kW。夏季熱負荷較少，冷負荷為50～350kW。由于負荷的波動較為明顯，因此，為了滿足不同時段內的負荷需求，本文系統內配備一定的電能存儲設備，增加系統的靈活性，提高系統的能源供應能力。根據本文所提出的風光出力區間數轉換，預測風機光伏的出力，形成上下限，考慮不確定性，形成出力的上下限。采用本文提出的魯棒優化方法將模型確定化處理。案例園區8760h的風機、光伏出力情況如圖3所示。光伏出力不確定性區間情況如圖4所示。

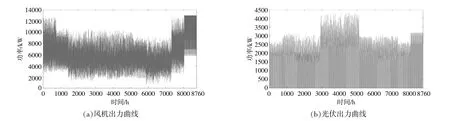
圖3 園區風電、光伏出力曲線Fig.3 Wind power and photovoltaic output curve in the park

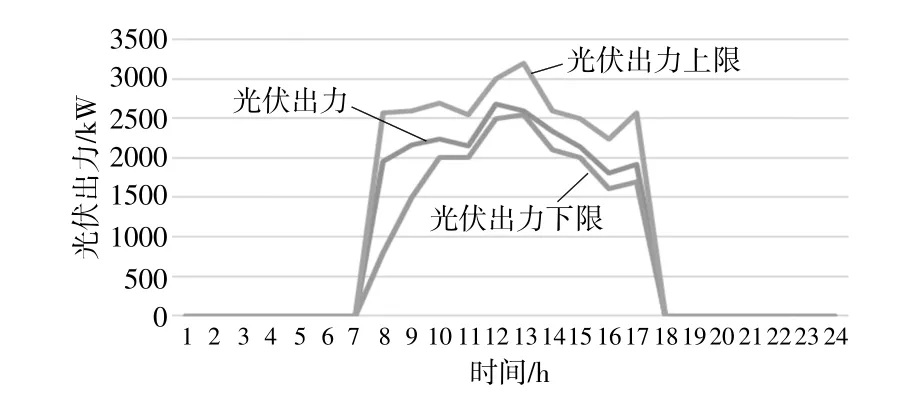
圖4 光伏出力不確定性區間圖Fig.4 Uncertainty interval diagram of photovoltaic output

各設備的相關參數如表1所示。

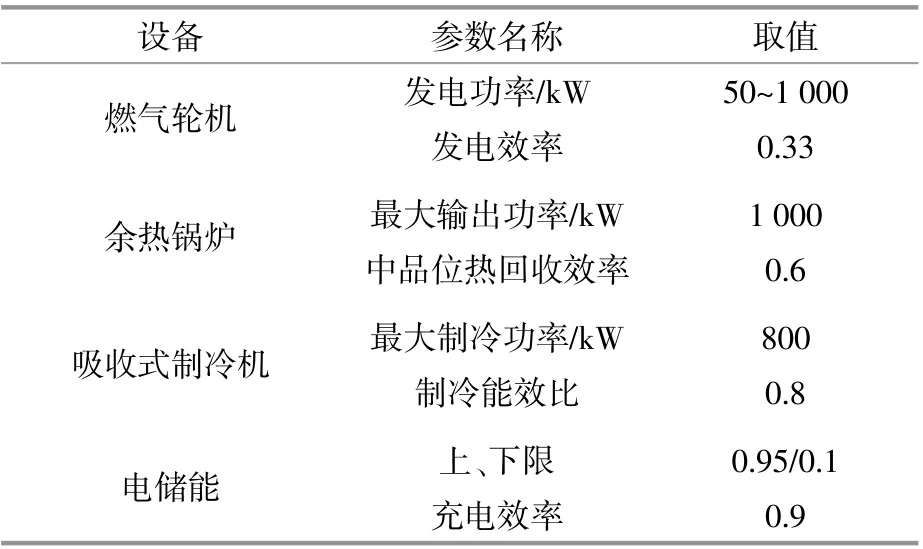
表1 設備參數Table1 Equipment parameter table

本次案例中的電價采用分時電價，不同時段的電價如表2所示。

表2 分時電價Table2 Time-of-use electricity price

在本算例中，主要將是否進行風光不確定性處理進行對比，分析進行風光不確定性處理的必要性，結果如表3，4所示。

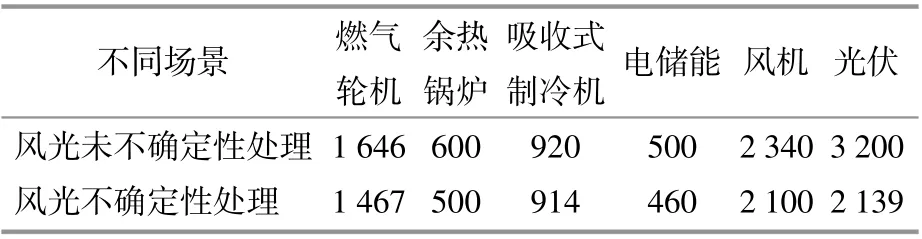
表3 不同場景的容量規劃結果Table3 Planning results for different scenarioskW

由表3可知，采用Matlab進行規劃模型求解，根據是否進行風光的不確定性處理，設備的規劃容量有所不同，規劃容量設計后，才能更好的對比不同場景規劃的經濟性與環境性的差別，更好的突出“雙碳”目標下，考慮風光不確定性對于逼近現實規劃場景的重要性。

以1m3天 然 氣 產 生2.063kg的CO2，1kW·h電產生0.98kg的CO2，分別求出在不同的場景中系統的CO2的排放量。根據表4，經過風光不確定性處理之后，年總成本和碳排放量均有所下降，分別下降20.2萬元和200kg，能源自給率提升了4.2%。

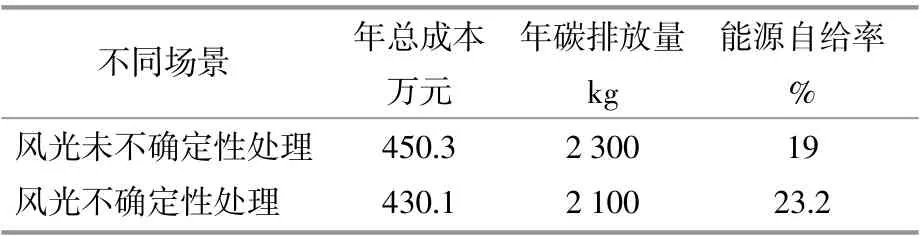
表4 不同場景規劃結果對比Table4 Comparison of planning results in different scenarios

將選取典型日作為分析對象，對規劃的結果進行分析，能夠計算出不同設備在典型日的運行出力曲線，如圖5，6所示。

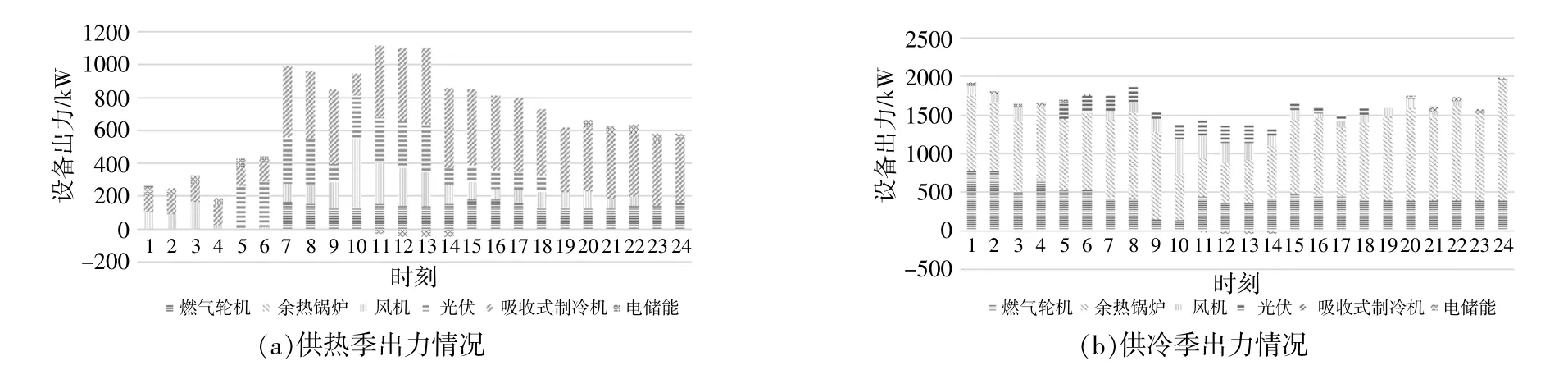
圖5 風光不確定性處理的出力情況Fig.5 An effort to deal with the uncertainty of scenery

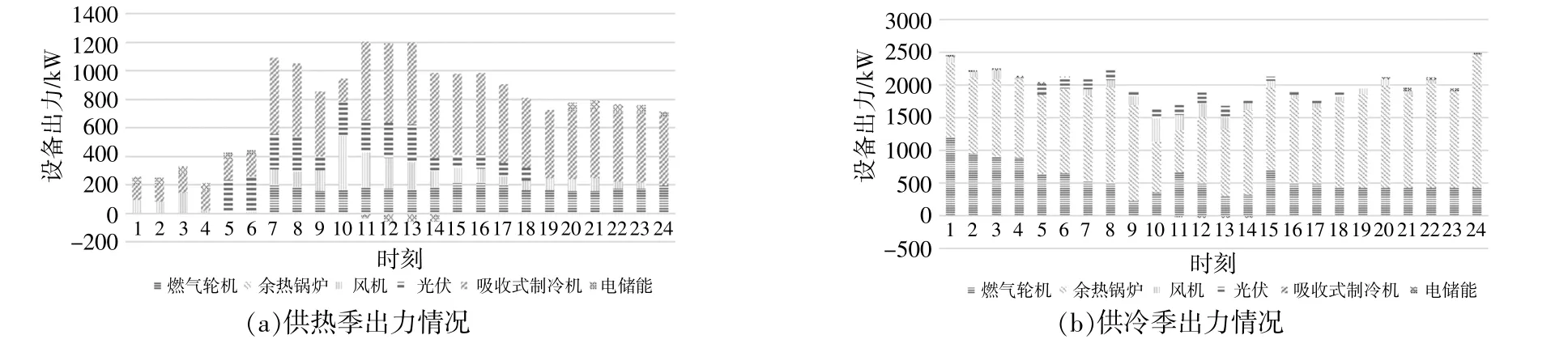
圖6 風光未不確定性處理的出力圖Fig.6 An effort to deal with the uncertainties of scenery

由圖5可以看出，當非低谷電價 （7：00-23：00）時，燃氣輪機在正常運行中的主要工作狀態是滿足電負荷。其中主要的處理情況是由風機出力與光伏出力和燃氣輪機滿足電負荷，考慮風光不確定性處理后，對于風光的能源利用更加精準，進而配置更加合適的電儲能，利用峰谷電價進行電價低谷時蓄電和高價時供電，同時存儲風光的多余電量，平抑風光的波動性。由于新能源能夠提供一定的系統用電量，所以在一定程度上降低系統對外購電量，但是熱負荷的需求維持穩定，進而會降低系統的從外網的購電量，燃氣輪機的輸出電功率在這種情況下也會出現一定程度的降低。供熱季，整體設備的出力情況大致相同，但由于進行風光不確定性分析和處理后，風光的出力情況會更加靠近實際情況，風機和光伏的出力都有一定程度的提升，并且更換為可再生能源的出力狀態仍滿足電負荷。在實際處理中，還需要考慮不確定性以及對不確定性的處理，因此風機光伏出力的預測值在一定程度上會存在些許誤差，這就需要開啟CCHP來增加備用空間。當不進行不確定性處理時，不需要多開啟CCHP備用，避免增加運行成本，但可以有助于減少棄光量，提升能源利用率。

為了研究風光出力波動性對實際調度結果的影響，本文在不同程度的風電出力預測偏差下，對進行風光不確定性處理與不進行處理的策略進行結果比較，以此判斷本文提出的魯棒優化處理的有效性。不同預測偏差下的成本如圖7所示。

由圖7可以得出，隨著風光出力預測偏差的增加，未進行不確定性處理和進行不確定性處理兩種狀態下的成本均增加，但其中經過風光不確定性處理優化的成本偏差比未經過不確定性處理的成本偏差的上升趨勢更緩慢，體現了考慮風光不確定性的必要性和有效性。

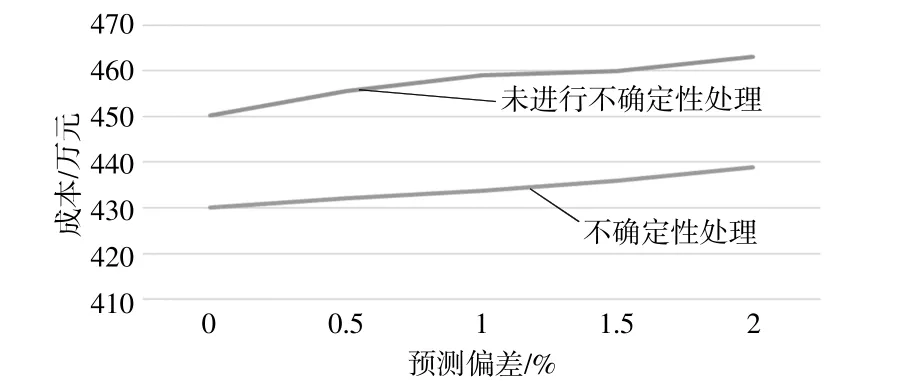
圖7 不同預測偏差下的成本Fig.7 Cost under different forecast deviations

5 結論

本文構建了“雙碳”目標下風光不確定性IES規劃模型，該模型是在充分考慮高滲透率的情況下，對可再生能源進行不確定性分析，借助實例對本文提出的優化模型進行驗證。結果表明，在對系統進行不確定性分析后，提高了可再生能源的消耗能力，通過對分時電價的利用，降低了系統的整體用能成本，同時降低了污染物的排放量，CO2的排放量降低8.7%。

①通過充分考慮風光不確定性并進行風光不確定性的處理，有助于解決風電消納和系統負荷波動的問題，有利于實現雙碳目標。②通過進行系統的不確定性分析，提高了可再生能源的消耗能力，降低了系統的整體用能成本，考慮風光不確定性的綜合能源系統更具有經濟優勢。③本文所提經濟性與環境性雙目標魯棒規劃方法，可以有效解決含不確定性的風光綜合能源系統容量優化配置問題，具有一定的工程參考價值。