里德堡原子超外差接收鏈路中的內稟增益系數研究*

吳逢川 安強 姚佳偉 付云起

(國防科技大學電子科學學院,電子科學系,長沙 410073)

里德堡原子利用其電磁誘導透明效應可以實時響應微弱的微波電場信號,實現空間微波電場信號的下變頻,作為超外差接收機使用.里德堡原子超外差接收機是由里德堡原子、光電探測器以及電子信息處理模塊等組成的新體制接收系統.目前,國內外學者對里德堡原子超外差接收技術的物理響應機理進行了深入研究,然而在缺乏完整的接收鏈路分析模型的指導下,不利于系統性能優化.本文從里德堡原子響應微波電場的物理機理出發,引入內稟增益系數的概念,建立并實驗驗證了里德堡原子超外差接收機的接收鏈路模型,簡要討論了內稟增益系數對系統靈敏度和響應特性的影響,為里德堡原子超外差接收系統性能優化提供理論指導.最后對里德堡原子接收鏈路和電子學接收鏈路的靈敏度性能進行了討論和對比.

1 引言

隨著量子微波測量技術的進一步深入發展,里德堡原子電磁誘導透明 (electromagnetic induced transparency,EIT)效應近年來在射頻微波領域備受關注.里德堡原子可以通過激光鎖頻并外加參考信號的方式構造里德堡原子超外差接收機,其在AM (amplitude modulation)和FM (frequency modulation)解調[1-6],QPSK (quad-phase shift keyed),QAM (quadrature amplitude modulation)

信號接收[7,8],頻譜分析[9],來波方向估計[10]等應用方面均有研究.相比于傳統電子學天線,采用里德堡原子對空間電磁波進行響應的優點之一是其不受工作波長限制,響應能力與傳感器尺寸無關[11];其次是里德堡原子具備超寬帶的工作頻帶,理論上可以實現甚低頻至紅外頻段內電場的響應[12,13],在不改變硬件的情況下,僅調節激光頻率即可改變里德堡原子響應的電場頻率;另外,由于傳感器中無金屬結構,且里德堡原子EIT 效應不通過強烈吸收空間電磁波能量來對空間電場進行響應,因此傳感器對待測電場擾動極小,可以實現全光無損探測[14];此外,該傳感器相比于傳統金屬天線具有更高的電場測量靈敏度性能,可以達到μV/m 量級[15-+].因此,里德堡原子用作新一代無線接收機具有巨大潛力.

目前研究中對里德堡原子超外差接收的物理響應機理進行了深入研究[20-25],然而其完整的接收鏈路模型尚未得到充分的研究和討論,不利于分析和優化里德堡原子超外差接收機的性能.以靈敏度為例,除里德堡原子自身的量子噪聲外,在里德堡原子超外差接收鏈路中也會引入額外的噪聲,這些噪聲的引入方式、環節略有不同,亟需一個完整的接收鏈路模型,分析這些噪聲對系統靈敏度性能的影響.對于里德堡原子超外差接收鏈路,其關鍵在于微波拉比頻率與探測光透射功率之間的映射關系,2020 年山西大學的景明勇等[18]提出了線性內稟增益系數(linear expansion coefficient)的概念,初步建立了二者的關系,但未對此概念進行實驗驗證,也未用于里德堡原子超外差接收鏈路的構建.

文中首先梳理了里德堡原子超外差接收機對微波待測信號的接收鏈路,引入內稟增益系數的概念,建立了里德堡原子超外差接收機對微波待測信號的接收鏈路模型;其次,通過實驗搭建里德堡原子超外差接收機,對接收模型進行實驗驗證;最后,通過分析該理論模型中的內稟增益系數,指出內稟增益系數對系統靈敏度和響應特性具有重要影響,可用于分析和優化里德堡原子超外差接收系統的性能.

2 里德堡原子接收機的架構以及工作原理

2.1 里德堡原子超外差接收機的架構

里德堡原子超外差接收機以里德堡原子為載體對微波信號進行接收,與傳統的電子學超外差接收機在原理上存在根本區別.其基本架構如圖1,主要分為三個部分: 里德堡原子、光電探測器、電子信息處理模塊.其中,里德堡原子由原子氣室進行封裝,通常為銫原子或銣原子蒸汽,在探測光和耦合光的共同作用下被激發至里德堡態,使之能夠響應微波電場,同時,引入一個微波參考信號照射原子氣室,用于控制里德堡原子的下變頻特性.當微波待測信號傳播至原子氣室中時,其內部的里德堡原子將待測信號中承載的信息轉移至從原子蒸汽中透射的探測光中,光電探測器進一步將透射的探測光中攜帶的信息轉移至光電流中,最終由電子信息處理模塊對光電流中攜帶的信息進行處理和讀取.與傳統的超外差接收機不同,里德堡原子超外差接收機在接收鏈路中有微波、探測光、光電流三種不同的信息載體,在接收鏈路中信息的載體經過了兩次轉換.

圖1 里德堡原子超外差接收機的架構Fig.1.Block diagram of Rydberg atomic superheterodyne receiver.

2.2 里德堡原子超外差接收機的工作原理

里德堡原子通常采用雙光子躍遷激發的方式制備,本文以銫原子為例,簡要介紹里德堡原子超外差接收機的工作原理.銫原子的階梯型四能級系統如圖2 中左上方框圖所示,利用波長為852 nm的探測光將銫原子從基態6S1/2激發至中間激發態6P3/2,采用波長為510 nm 的耦合光將銫原子從中間激發態6P3/2激發至里德堡態44D5/2,此時探測光的透射率增強,掃描耦合光或者探測光頻率可以觀測到852 nm 附近的探測光形成EIT 透射峰.在此基礎上,添加頻率為8.568 GHz 的共振微波場,將里德堡態44D5/2和里德堡態45P5/2進行耦合,此時掃描耦合光或者探測光頻率可以觀測到EIT 透射單峰分裂為雙峰,產生AT 分裂效應.

探測光頻率鎖定在基態能級|1 〉和中間態能級|2 〉的共振躍遷頻率,微波場頻率為里德堡能級|3 〉和|4 〉的共振頻率,掃描耦合光頻率,對應不同的電場強度E的EIT 光譜理論計算結果如圖2 中間各組雙峰曲線所示,兩峰之間的間距隨著微波場的場強E增大而增大.兩峰之間的間距即為微波場的拉比頻率ΩMW,ΩMW與E的關系可表示為

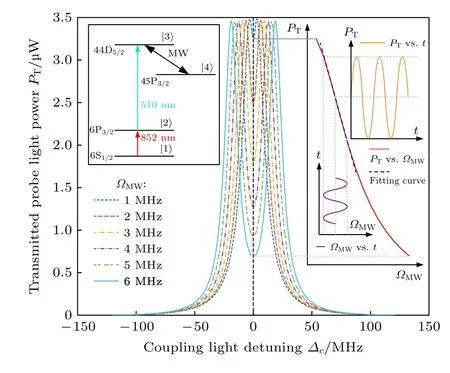
圖2 里德堡原子對微波信號的響應機理Fig.2.Response mechanism of Rydberg atom to microwave signal.

其中 ? 為約化普朗克常量;μMW為微波場的躍遷偶極矩.

假設此時空間中存在兩個頻率差為Δf的微波信號ELO和ES,其中ELO為參考微波信號,ES為待測微波信號,電場強度的時域表達式分別為

其中A,B分別為ELO和ES的電場強度;fLO和fs分別為ELO和ES的頻率;φLO和φs分別為ELO和ES的相位.疊加場可以表示為級數展開的形式:

其中x=B/A,Δφ=φLO—φs,Δf=fLO—fs,里德堡原子對ELO和ES疊加場Etotal的非線性響應,可以等效為包絡檢波.當x?1 時,疊加場包絡幅度的波動頻率分量主要為ELO和ES的差頻Δf,高次諧波分量可忽略不計.結合(1)式和(4)式,可得到A?B時微波電場的拉比頻率ΩMW隨時間t的變化規律:

其中微波拉比頻率ΩMW的直流分量ΩDC和交流分量ΩAC分別為

ΩDC和ΩAC分別包含ELO和Es的電場強度信息.

當鎖定耦合光的頻率至中間態能級|2 〉和里德堡能級|3 〉的躍遷頻率,如圖2 中黑色虛線所示,提取不同微波拉比頻率下耦合光鎖定頻點處的透射探測光功率,可得到透射探測光功率PT與微波拉比頻率ΩMW的關系曲線,如圖2 右側直角坐標系中曲線所示.其中紅色曲線描述探測光透射功率PT與微波拉比頻率ΩMW之間的關系,藍色虛線為橙色曲線的線性擬合結果,紅色曲線左下方紫色正弦函數曲線描述了微波拉比頻率ΩMW隨時間t的變化,紅色曲線右上方橙色正弦函數曲線描述了探測光透射功率PT隨時間t的變化.由圖2 右側坐標軸中的曲線可以發現,透射的探測光功率隨著微波拉比頻率的增大而減小,且在一定范圍內透射探測光的功率與微波拉比頻率呈線性關系,即藍色虛線與紅色曲線重合的范圍.當微波場強過小或過大,受到EIT-AT 分裂光譜形狀的影響,微波場強與探測光的透射功率將呈現明顯的非線性關系.

當ΩDC選擇適當,使得透射探測光功率與微波拉比頻率ΩMW關系處于線性區間內時,疊加一個小的交流分量ΩAC,微波的總拉比頻率ΩMW隨時間變化的關系曲線如圖2 中左下方紫色曲線所示,通過紅色曲線可以將其映射為透射探測光功率隨時間的變化曲線(暫不考慮原子的瞬時帶寬,假設原子響應的速度比微波拉比頻率變化的速度快),如圖2 中右上方橙色曲線所示.其表達式為

其中aΩDC決定透射探測光功率的直流分量PTDC,系數a為直流分量的微波拉比頻率ΩDC與探測光透射功率直流分量PTDC之比,為ΩDC的函數.κΩAC決定探測光透射功率的交流分量PTAC,其包含待測微波信號的電場強度信息,因此,我們只討論透射探測光功率的交流分量PTAC.其中|κ|為由探測光透射光譜引入的內稟增益系數,即激光鎖頻點處透射光功率隨微波拉比頻率的變化速率.

理論上,當微波頻率處于躍遷頻率時,掃描耦合光所得的EIT-AT 光譜曲線可以由兩個相同的單峰曲線(通常為Voigt 函數曲線)組合而成.因此當探測光和耦合光均鎖定在躍遷頻率上時,內稟增益系數κ可以理解為單峰曲線在激光鎖頻點處的斜率.

進一步地,透射探測光由光電探測器接收,轉換為光電流信號輸出,透射探測光信號功率的交流分量與光電二極管輸出光電流信號功率的交流分量IAC之間的關系可表示為

從(9)式可知,待測微波電場信號的載體從探測光轉移至光電探測器的光電流,其中D為光電二極管的響應度.光電探測器輸出光電流信號交流分量瞬時功率為

其中RL為光電探測器的輸出電阻,由(10)式可進一步推導得到里德堡原子響應Es的電場強度B和光電探測器輸出的電信號功率有效值Pout的關系:

其中G為光電流經過后級電路處理的增益;當ΩDC選取適當使得里德堡原子工作于線性區間時;κ的值基本不變,因此(11)式中除待測微波信號電場強度B外,均為常量,可采用系數C1綜合表示.

綜上所述,里德堡原子超外差接收鏈路對微波待測信號的處理流程可以用圖3 進行表示.微波待測信號的電場強度經里德堡原子映射成為微波拉比頻率的波動,并在探測光和耦合光鎖頻后進一步映射成為探測光透射功率的波動,進而通過光電探測器映射成為光電流信號的波動,光電流波動幅度的平方與輸出光電流信號功率成正比.

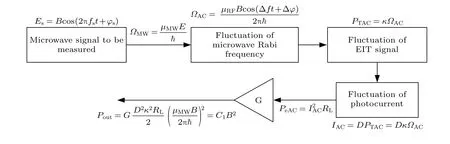
圖3 里德堡原子超外差接收機對微波待測信號接收的流程Fig.3.The process of receiving microwave signal to be measured by Rydberg atomic.superheterodyne receiver.

上述流程中,微波待測信號場強與微波拉比頻率之間的關系、入射至光電探測器中的探測光功率與光電流之間的關系、光電流大小與光電流信號功率之間的關系均有成熟的理論支撐和實驗驗證,可通過系統的工作頻率以及硬件參數確定.而對于微波拉比頻率的波動與探測光透射功率波動之間的關系,即內稟增益系數κ,尚缺乏實驗驗證.

3 實驗測試

為驗證內稟增益系數κ及系統接收鏈路模型的合理性,本文在實驗上建立了里德堡原子響應的電場強度和電子信息處理模塊讀取信號功率的關系,并進行了系統靈敏度的測量.

3.1 實驗系統

實驗系統如圖4 所示,實驗系統中采用兩部獨立的信號源SG1 和SG2 分別產生參考電場信號ELO和待測電場信號Es,并利用同步信號將兩臺信號源進行同步以保證ELO和Es相位差穩定.兩路信號通過一個功分器合成一路信號,并通過喇叭天線輻射至原子氣室.852 nm 的探測光和510 nm 的耦合光共線反向傳播穿過原子氣室,將氣室內部的銫原子蒸汽激發至里德堡態,兩束激光均鎖定至里德堡原子四能級系統的躍遷頻率處.透射原子氣室的探測光信號使用光電探測器接收并轉換為光電流信號,光電流信號輸入至信號分析儀中記錄得到光電流信號交流分量的功率.實驗中,探測光功率為22 μW,耦合光功率為55 mW,探測光和耦合光光束的1/e2半徑分別為0.4 mm,0.7 mm;SG1的發射頻率為8.568 GHz,SG2 的發射頻率為8.568 GHz+10 kHz,SG2 發射功率為3 dBm.

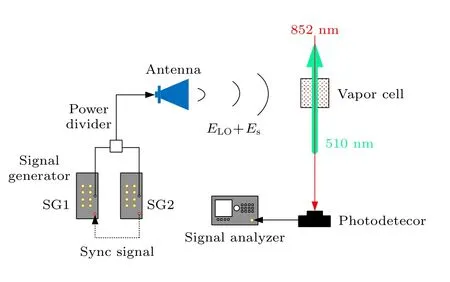
圖4 實驗系統框圖Fig.4.Block Diagram of Experimental System.

3.2 校準實驗

為實驗獲得里德堡原子響應的微波電場強度和信號分析儀顯示功率的關系,首先需要校準兩個關系: 1) 信號源發射功率與原子響應的拉比頻率(或電場強度)之間的關系;2) 信號源發射功率與信號分析儀讀取的信號功率之間的關系.通過這兩個關系,推導得到實驗系統中里德堡原子響應的微波電場強度和信號分析儀讀取的光電流交流信號功率的關系.

傳統的方法根據標準天線公式(IEEE Std 1309-2013)估計在目標位置的電微波拉比頻率,其公式如下:

其中η為自由空間波阻抗;g為天線增益;αl為信號源到天線的插損;PSG為信號源發射功率;d為天線到目標位置的距離.

然而,受原子氣室的駐波效應以及實驗空間中其他物體散射的影響,采用標準天線公式估計原子氣室位置處電場強度幅值是不準確的.因此(12)式應修正為

其中F為考慮實際環境的中電磁波的散射、繞射以及駐波后的修正因子.在相對固定的實驗條件下,除PSG為變量外,其余系數均為常數,因此可以將這些系數綜合為一個常數C2.

由于影響C2值的因素較多,理論計算比較困難,本文通過EIT-AT 光譜測量獲得多組不同PSG下對應的微波拉比頻率ΩMW,利用函數擬合確定C2的值.對ELO和Es的實驗校準結果如圖5 所示,其中藍色帶誤差棒的曲線為實驗測量結果,紅色曲線為函數擬合結果,對于兩部信號源,函數擬合得到的系數C2均為8 MHz/mW1/2.

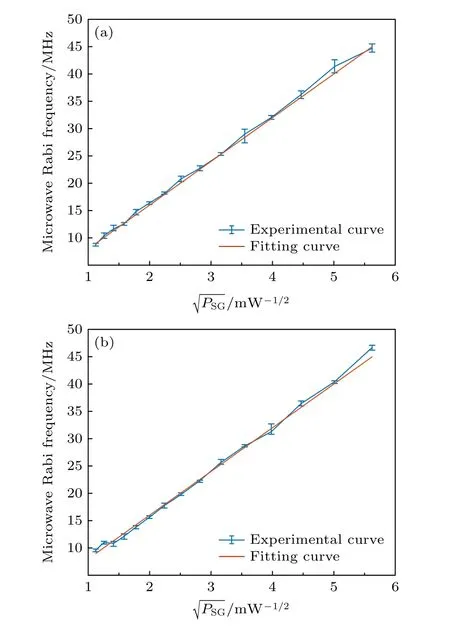
圖5 信號源發射功率與里德堡原子響應的微波拉比頻率關系 (a) 微波參考信號;(b) 微波待測信號Fig.5.Relationship between the emission power and the microwave Rabi frequency: (a) Microwave reference signal;(b) microwave signal to be measured.

此外,對于一個固定的實驗場景,信號源的發射功率PSG與信號分析儀讀取的光電流信號的功率PSA之間的關系是固定的.通過信號源SG2 產生不同的發射功率PSG,記錄信號分析儀讀取的信號功率PSA,并利用函數擬合得到PSA和PSG之間的關系.如圖6 所示,藍色帶誤差棒的曲線為實驗測試結果,從實驗結果可以看出二者為線性關系.紅色曲線為函數擬合結果,由擬合結果可得

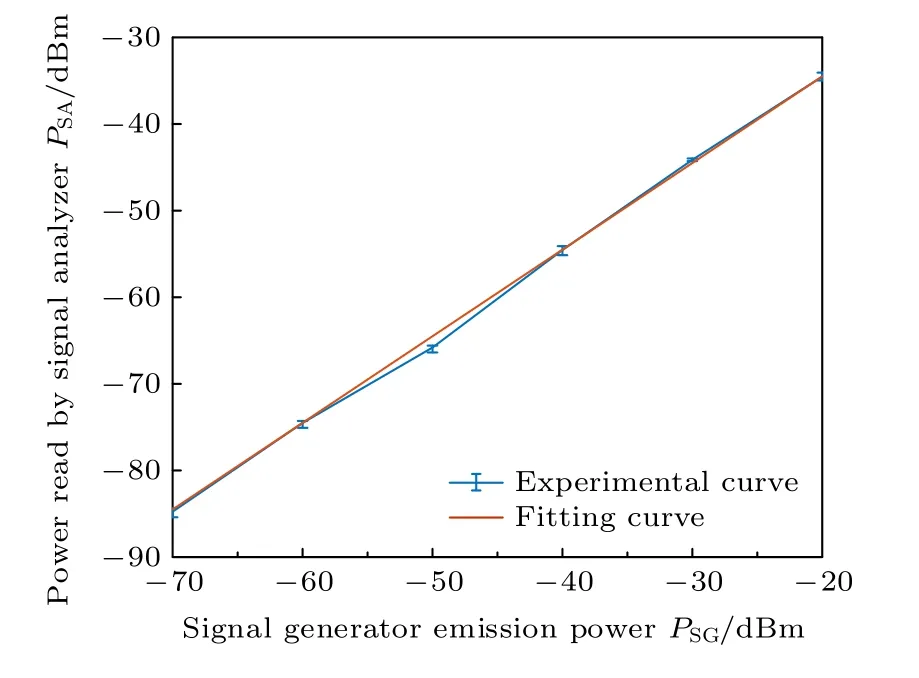
圖6 信號源設置功率與信號分析儀讀取功率關系Fig.6.Relationship between the emission power and the power read by the signal analyzer.

其中系數C3=0 .03548.由(13)式和(14)式可以得到里德堡原子響應的待測微波電場強度B與信號分析儀讀取功率PSA之間的關系:

由于(15)式中除PSA外其余參數均為常數,因此可以將這些參數綜合為一個常數C4.

實驗中采用的里德堡能級對應的微波電場躍遷偶極矩μMW=1255.5qa0,q為基本電荷量,a0為玻爾半徑.根據前面實驗測量得到的C2和C3,可以計算得到C4=83.6024 W1/2·A—1·m—1.

另一方面,根據實驗系統同樣可以計算(11)式中的系數C1,其中實驗采用的Throlabs PDA36A2型號光電探測器對波長為852 nm 的探測光響應度為D=0.55 A/W,其內置放大器增益G=50 dB,光電探測器輸出電阻RL=50 Ω.對于κ,可以采用Voigt 函數擬合實驗結果計算得到,如圖7 所示.圖7 中紅色和藍色虛線分別為兩個形狀相同的Voigt函數曲線,其相對于耦合光失諧量Δc=0 處對稱,橙色雙峰曲線為上述兩個Voigt 函數曲線擬合的結果,紫色曲線為微波參考信號發射功率為3 dBm時的實驗實測結果,粉色曲線為對圖7中紅色虛線代表的Voigt 函數進行求導計算的結果.橙色曲線與紫色曲線在透射光譜腰部有較好的擬合,因此在一定程度上可以采用Voigt 曲線對實驗所得光譜進行描述,在鎖頻點處(Δc=0)粉色虛線對應的值即為內稟增益系數κ.表1 為多次測量EIT 光譜計算得到的κ,C1,以及C4—2與C1之間的誤差值.

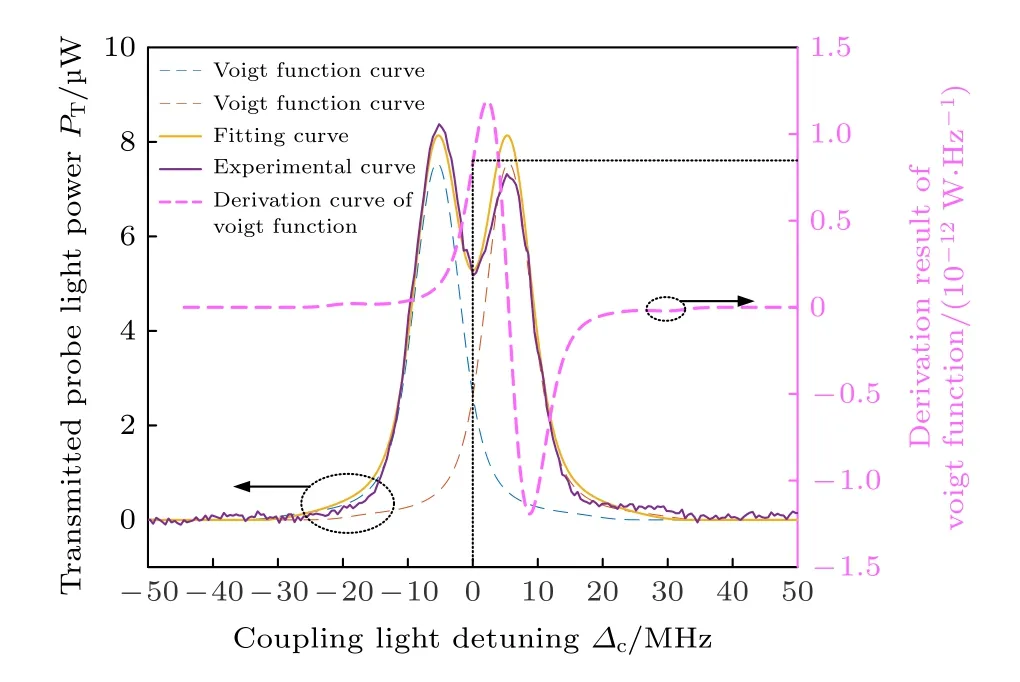
圖7 采用Voigt 曲線對實驗所得EIT-AT 分裂光譜曲線進行擬合Fig.7.Fitting the experimental EIT-AT split spectrum curve with Voigt curves.

通過表1 可以看出相對誤差值不超過8%,誤差主要來自于激光鎖定頻率和功率的漂移以及曲線擬合帶來的誤差.結果表明,(15)式與(11)式基本等價,證明了當激光鎖定在躍遷頻率處時,κ的值為單個Voigt 函數曲線在鎖頻點處斜率的絕對值.

3.3 靈敏度測量

通過理論推導和實驗驗證確定了κ值的大小后,為驗證里德堡原子超外差接收鏈路模型的合理性,本文進一步測量了系統的噪底,并分別采用(11)式和(15)式計算該系統的電場測量靈敏度.

在里德堡原子超外差接收機的激光參數以及信號源功率SG1 的發射功率不變的實驗條件下,關閉SG2 信號源,信號分析儀(分辨率帶寬為1 Hz)對里德堡原子超外差接收機系統噪底的測量結果如圖8 所示,10 kHz 處的噪底功率譜密度為—103.4 dBm/Hz.

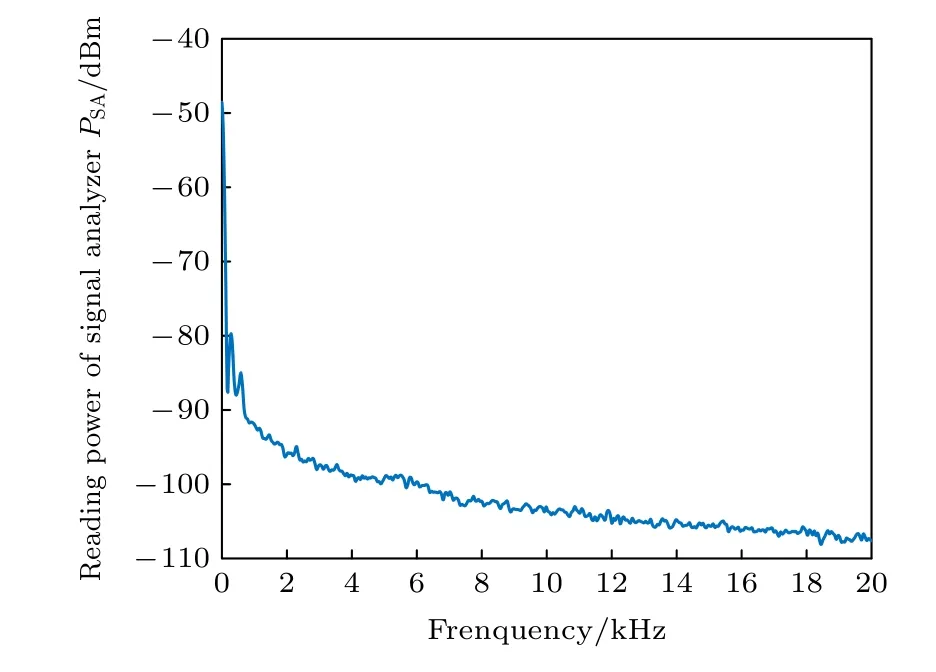
圖8 里德堡原子超外差接收機系統噪底Fig.8.The system noise floor of Rydberg atomic superheterodyne receiver.

將表1 中所有κ的值以及上述測量得到的10 kHz 處的噪聲功率譜密度的值代入(11)式中,計算得到的里德堡原子超外差接收機的靈敏度范圍為178.1—189.68 nV·cm—1·Hz—1/2.利用(15)式計算可得,里德堡原子超外差接收機的電場靈敏度為182.9 nV·cm—1·Hz—1/2,其值落于由(11)式計算的靈敏度范圍內且誤差不大,這說明該理論模型可以用于分析里德堡原子超外差接收機系統的電場靈敏度.

表1 計算得到的κ,C1,以及C4—2 與C1 之間的誤差值Table 1.Calculated κ,C1,and the error between C4—2 and C1.

4 內稟增益系數對系統性能的影響

為探索內稟增益系數對系統特性的影響,采用量子光學半經典理論設計了相同透射光譜強度、不同線寬的兩種EIT-AT 透射光譜模型,簡要討論了內稟增益系數對系統靈敏度特性以及線性響應特性的影響.最后對里德堡原子超外差接收系統和傳統電子學接收系統的靈敏度性能進行了比較.

4.1 靈敏度特性

在不考慮原子熱運動帶來的多普勒、碰撞以及渡越等光譜展寬因素的條件下,設計如圖9 中右上方直角坐標系中所示的兩個EIT-AT 光譜曲線模型,兩種曲線模型的透射光譜高度一致,區別在于模型1(綠色實線)光譜寬度相比于模型2(紅色虛線)光譜寬度要寬.通過鎖定探測光和耦合光失諧量Δp=Δc=0,改變微波拉比頻率ΩMW,分別得到圖9 模型1 和模型2 中探測光透射功率PT與微波拉比頻率ΩMW的關系,如圖9 中暗綠色實線和暗紅色虛線所示.通過對暗綠色實線和暗紅色虛線分別求導可知,在線性區內內稟增益系數κ的最大值分別為1.319 W/Hz 和4.636 W/Hz,其對應的微波拉比頻率分別為0.908 MHz 和0.372 MHz.

為直觀地說明內稟增益系數κ對系統靈敏度的影響,假設此時存在兩組隨時間t變化的微波拉比頻率,分別為ΩMW1和ΩMW2,如圖9 左下方兩個紫色正弦函數曲線,其波動幅度大小一致且均分別處于模型1 和模型2 的線性區,可以發現由紅色虛線映射得到的探測光透射功率PT的隨時間t的波動幅度相比于綠色實線映射得到的結果要大,如圖9 右上方橙色曲線所示.因此,κ的值越大,里德堡原子對微波的響應能力越強.

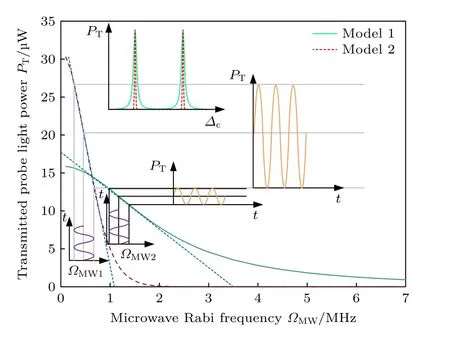
圖9 不同內稟增益系數對探測光透射功率波動大小的影響Fig.9.The influence of expansion coefficient on the fluctuation of transmission power of probe laser.

進一步地,在里德堡原子超外差接收鏈路中光電流輸出環節,引入電子噪聲功率譜密度n,可以得到單位頻率下光電探測器的輸出信噪比SNR:

當SNR=1 時,可以得到單位頻率下最小可測量電場強度,即系統的靈敏度:

當選定里德堡原子的能級系統以及光電探測器型號后,除κ和n外,其余系數可視為常數.從(16)式和(17)式可以看出,在保持n不變時,κ的值越大,即探測光透射光譜斜率越大,對后級電子噪聲的壓制效果越好,最小可測量電場強度越小,系統靈敏度性能越好.考慮n為經典熱噪聲極限下的噪聲功率譜密度,常溫下為—174 dBm/Hz,RL,D,μMW的值與第3 節實驗一致.由(17)式計算得到在經典熱噪聲極限下的系統靈敏度的極限與探測光透射光譜斜率的關系如圖10 所示,圖10 中內稟增益系數κ的取值范圍為5×10—14—5×10—11W/Hz,計算得到系統靈敏度可能的極限范圍為1.4—0.14 nV·cm—1·Hz—1/2,激光鎖定點處的探測光透射光譜斜率增大一個數量級,則系統靈敏度性能將提高一個數量級,因此內稟增益系數κ對系統靈敏度性能具有重要影響.

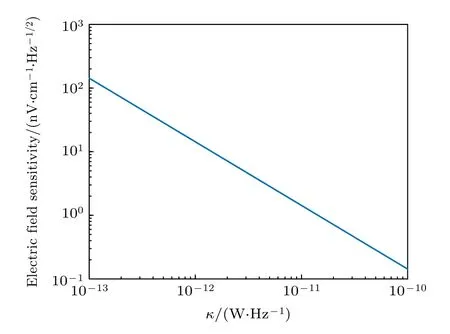
圖10 內稟增益系數和里德堡原子接收機系統靈敏度之間的關系Fig.10.Relationship between the expansion coefficient and sensitivity of the Rydberg atomic receiving system.

4.2 線性響應特性

線性響應特性是接收機的重要指標之一,在接收機線性響應特性較差時,會表現出明顯的高次諧波分量,而高次諧波在接收系統中通常被視為干擾,可以在后級電子信息處理模塊中添加低通濾波器進行濾除,然而當微波待測信號為具有一定帶寬的調制信號時,高次諧波可能與基頻信號的頻帶產生重疊,無法用低通濾波器進行濾除,則需要對內稟增益系數進行設計,使得里德堡原子具有更好的線性響應特性.

為直觀地說明內稟增益系數κ對系統線性響應特性的影響,與圖10 類似,選取相同波動幅度的微波拉比頻率ΩMW1和ΩMW2,使二者的直流分量ΩDC1和ΩDC2分別處于模型1 和模型2 的線性區中,如圖11 中兩組紫色正弦函數曲線.從圖11中可以看出,雖然由暗紅色虛線映射得到的探測光透射功率PT的波動幅度相比于暗綠色實線映射得到的結果較大,但是其信號發生了失真,產生了明顯的高次諧波,無法保證系統良好的線性響應特性.

為進一步明確不同內稟增益系數的模型的線性響應特性的區別,本文設計微波拉比頻率ΩMW1和微波拉比頻率ΩMW2的直流分量分別為ΩDC1=0.908 MHz,ΩDC2=0.372 MHz,即分別處于模型1 和模型2 的最佳靈敏度工作點;交流分量ΩAC1和ΩAC2分別為變量.ΩMW1(ΩMW2)通過圖11 中綠色實線(紅色虛線)的映射,可以得到交流分量ΩAC1(ΩAC2)和與之對應的探測光透射功率交流分量PTAC1(PTAC2).將PTAC1和PTAC2進行快速傅里葉變換(fast Fourier transform,FFT),可以得到二者FFT 結果與ΩAC的關系,如圖12 所示.圖12 中藍色實線代表基頻分量PFF與ΩAC的關系,紅色虛線代表二次諧波分量PSH與ΩAC的關系,由圖12 可知基頻分量PFF和二次諧波分量PSH均隨ΩAC增大而增大.

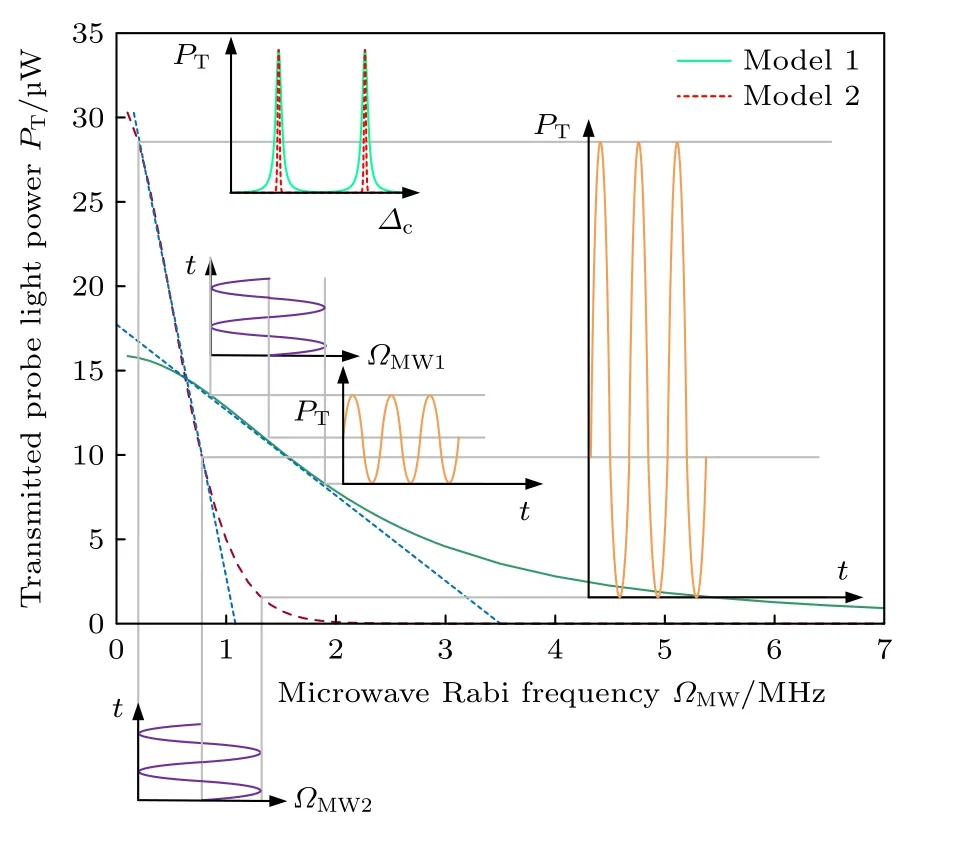
圖11 不同內稟增益系數對線性特性的影響Fig.11.The influence of expansion coefficient on linear characteristic.

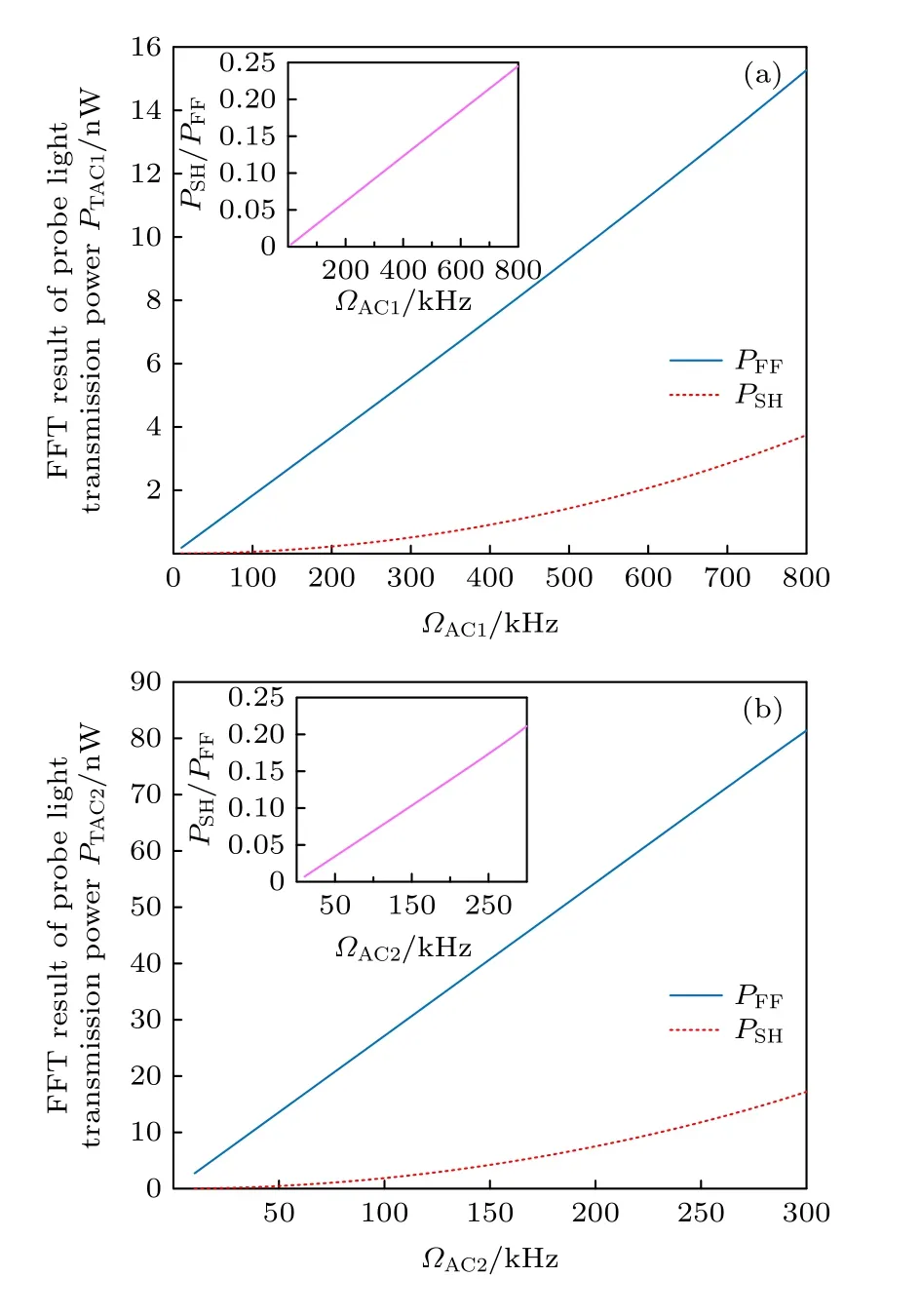
圖12 ΩAC 和PTAC FFT 結果之間的關系 (a) ΩAC1 vs PTAC1;(b) ΩAC2 vs PTAC2Fig.12.Relationship between ΩAC and FFT results of PTAC: (a) ΩAC1 vs PTAC1;(b) ΩAC2 vs PTAC2.

在ΩAC1、ΩAC2取值相同的條件下,PTAC1的傅里葉變換結果中的基頻分量PFF比PTAC2的傅里葉變換結果中的基頻分量PFF大.然而,從圖16中左上方PFF與PSH的比值與ΩAC的關系曲線(粉色實線)可以看出,在ΩAC相等的條件下,模型1中PFF與PSH的比值相比于模型2 的更小,模型2具備更好的線性特性.

綜上所述,在EIT-AT 透射光譜高度相等時,增大內稟增益系數κ的值(減小EIT-AT 透射光譜線寬),可以對后級電子噪聲起到壓制效果,在一定程度上提高系統的靈敏度,但僅在微波待測信號場強范圍較小時能獲得較好的線性特性;減小內稟增益系數κ的值(增大EIT-AT 透射光譜線寬),可以在更大的微波待測信號場強范圍內獲得良好的線性特性,但靈敏度性能會有所下降.因此,對內稟增益系數,需要根據里德堡原子超外差接收鏈路的使用場景進行設計,優化靈敏度和線性響應特性.

4.3 里德堡原子接收機和傳統電子學接收機靈敏度性能的比較

里德堡原子接收機和傳統電子學接收機由于工作機理上的差別,對于其靈敏度性能衡量的標準也不同.對于里德堡原子通常采用電場靈敏度進行衡量,而電子學接收機通常采用功率或者功率譜密度對靈敏度進行衡量.此外,對于里德堡原子,其原子氣室部分直接與外部環境耦合,無法如傳統電子學接收機通過接入匹配負載來對外部噪聲進行隔離.因此,為統一二者的衡量標準,需要給傳統接收機引入一個天線結構,使得傳統接收機的靈敏度衡量標準可以由功率譜密度轉換為電場靈敏度.由于里德堡原子對微波電場極化敏感,可以假設引入的天線為一個無耗的電小天線,其增益為Gant=3/2[26].

另一方面,由級聯噪聲系數公式可知電子學接收機中前級射頻元件的噪聲系數對系統內部噪聲性能的影響最大,當接收系統中天線后緊接著連接低噪放且在低噪放增益較高時,低噪放的噪聲性能基本可以代表整個系統的內部噪聲性能.此處假設天線接收下來信號后緊接著采用低噪放進行放大,且采用的低噪放增益較高,低噪放的噪聲性能可以代表整個電子學接收機的內部噪聲性能.

基于上述假設,里德堡原子超外差接收機和傳統電子學接收機的內部噪聲性能存在兩種比較方法: 1) 將二者的內部噪聲均通過接收鏈路轉化為電場靈敏度進行衡量;2) 將二者的內部噪聲均采用等效噪聲溫度進行衡量

設低噪放在室溫下的等效噪聲溫度Te=100 K,由噪聲系數的定義以及噪聲系數與噪聲溫度的關系可知,在室溫T0=290 K 條件下,且輸入低噪放的資用熱噪聲功率譜密度為—174 dBm/Hz 時,只有當輸入至低噪放的信號功率譜密度大于—172.7 dBm/Hz 時,低噪放在單位頻率下的輸出信噪比才可能大于1.

對于里德堡原子接收系統,根據文中實驗系統參數,設光電二極管輸出的噪聲功率譜密度為n=—172.7 dBm/Hz,由(17)式可得到里德堡原子系統內部噪聲對應的電場靈敏度,約為19.4 nV·cm—1·Hz—1/2.

另一方面,對于電子學接收系統,設經過天線接收并輸入至低噪放的噪聲功率譜密度為n=—172.7 dBm/Hz,由天線接收單位頻率下電場信號強度E和天線接收下來的功率p的關系:

其中λ0為工作頻率在自由空間中的波長,根據實驗中采用的頻率8.568 GHz,可以得到電子學接收系統對應的電場靈敏度,約為1.72 nV·cm—1·Hz—1/2.即對于該實驗系統,里德堡原子接收機的電場靈敏度性能還需要提高約11 倍,才能與等效噪聲溫度為100 K 的電子學接收系統的靈敏度性能相當.

以等效噪聲溫度為標準衡量時,設電子學接收機電場靈敏度為19.4 nV·cm—1·Hz—1/2,由(18)式以及噪聲系數與噪聲溫度的關系,可以得到電子學接收機的等效噪聲溫度僅需要達到Te=49447 K,即可達到與該實驗系統下里德堡原子接收機在等效噪聲溫度為Te=100 K 時相當的靈敏度性能.

除增大內稟增益系數,通過在原子氣室處添加諧振結構,對原子氣室中的信號電場進行諧振增強,也有望達到并超越現有電子學接收機的靈敏度性能[27,28].理論上原子氣室受到外部環境噪聲(如黑體輻射和真空漲落)的影響,當內部噪聲受到足夠強的壓制,外部環境噪聲將變成影響靈敏度的主要因素,對此可通過仔細設計諧振結構的品質因數來盡可能減小外部環境噪聲的影響[29].

5 結論

本文通過引入內稟增益系數,建立了完整的里德堡原子超外差接收鏈路模型,通過實驗搭建里德堡原子超外差接收機來對系統接收鏈路模型的合理性進行了驗證,并簡要討論分析了內稟增益系數對里德堡原子超外差接收鏈路的靈敏度以及線性響應特性的影響,為下一步優化里德堡原子超外差接收系統性能提供理論依據和方法途徑.最后對里德堡原子超外差接收機和電子學接收機靈敏度性能進行了簡要討論和對比,指出可通過諧振結構設計來進一步提高里德堡原子接收機的靈敏度性能.