函數插值分析研究與應用

郭佳欣

（北京建筑大學，北京 102616）

實際問題中經常有這樣的函數y=f(x)，其在某個區間[a，b]上有有限個離散點x0,x1,…xn，且這些點對應函數值為yi=f(xi)(i=0,1,2...)，若想得到其它點的值就必須找一個滿足上述條件的函數表達式。

1 Lagrange 插值函數

1.求作n 次多項式pn(x)，使滿足條件：

這就是所謂的拉格朗日（Lagrange）插值。點xi（它們互不相同）稱為插值節點。用幾何語言來表達這類差值，就是通過曲線y=f(x)上給定的n+1 個點(xi,yi)(i=0,1,...,n)，求作一條n 次代數曲線y=pn(x)作為y=f(x)的近似。

2.拉格朗日插值公式。

（1）首先考察線性插值的簡單情形。若y=f(x)表示過兩點(x0,y0),(x1,y1)的直線，這個問題是我們所熟悉的，它的解可表示為對稱式：

此類為一次插值，稱為線性插值。若令：

由此可得：l0(x0)=1,l1=(x1)=1,l1(x0)=0，則有：p1(x)=l0(x)y0+l1(x)y1，這里的l0(x),l1(x)可以看作是滿足條件l0(x0)=1,l0(x1)=0l1(x1)=1,l1(x0)=0的插值多項式，這兩個特殊的插值多項

式稱作上述問題的插值基函數[1-2]。

（2）拋物插值。線性插值僅僅利用了兩個節點的信息，精度自然很低，為了提高精度，進一步考察二次插值。若y=f(x)表示過三點(x0,y0),(x1,y1),(x2,y2)的曲線，求它的解。二次插值的幾何解釋是，用通過三點(x0,y0),(x1,y1),(x2,y2)的拋物線y=p2(x)來近似所考察的曲線y=f(x)，因此這類插值亦稱為拋物插值。

根據上述解決方法，同理可以得出：

容易看出，這樣構造的p2(x)為問題的解。

（3）推廣到一般：已知函數在n+1 個不同點x0,x1,...xn上的函數值分別為y0,y1,...yn求一個次數不超過n 的多項式pn(x)，使其滿足：pn(xi)=yi(i=0,1,...n)即n+1 個不同的點可以決定的一個n 次多項式。過n+1 個不同的點分別決定n+1 個n 次插值基函數。l0(x),l1(x),...ln(x)每個插值基多項式滿足：a.li(x)是n 次多項式；b.li(x)=1，而在其它n 個點li(xk)=0,(k≠i)。由于li(xk)=0,(k≠i)，故有因子(x-x0)...(x-xi-1)(x-xi+1)...(x-xn)因其已經是n 次多項式，故而僅相差一個常數因子。令li(x)=a(x-x0)...(x-xi-1)(x-xi+1)...(x-xn)由li(xi)=1，可以定出a,進而得到：

則n 次拉格朗日型插值多項式pn(x)=y0l0(x)+y1l1(x)+...ynln(x)，從而pn(x)是一個次數不超過n 的多項式，且滿足pn(xi)=yi(i=0,1,...n)[3-5]。

2 Newton 插值函數

2.1 Newton 法的簡述

設(x-xk)是f(x)的一個近似根，把f(x)在xk處泰勒展開：

若取前兩項來近似代替f(x)，則f(x)=0 的近似方程為f(x)=f(xk)+f'(x)(x-xk)=0。設f'(x)≠0，設其根為xk+1，則xk+1的計算公式為：

這即為牛頓法，其迭代函數為：

牛頓法其實是一種逐步的線性化的方法，它的本質是將f(x)=0 非線性方程的求根問題歸結為類似的一系列的線性方程f(xk)+f'(x)(x-xk)=0 的根。

2.2 具有承襲性的插值公式

先考察線性插值的插值公式：

由于p0(x)=f(x0)可看作是零次插值多項式，上式表明p1(x)=p0(x)+c1(x-x0)其中，修正項的系數：

再修正p1(x)以進一步得到拋物插值公式的解p2(x),為此，令：

顯然，不管系數c2 如何取值，p2(x)均能滿足兩個條件：p2(x0)=f(x0),p2(x1)=f(x1)，再用剩下的一個條件p2(x2)=f(x2)來確定c2，結果有：

記c0=f(x0)，從而有：p2(x)=c0+c1(x-x0)+c2(x-x0)(x-x1)

以上論述表明，為了建立具有承襲性的插值公式，需要引進差商并研究其性質。

2.3 差商及其性質

對于給定的函數f(x),記f(x0,x1,...,xn)表示關于節點x0,x1,...,xn的n 階差商。一階差商定義為：

二階差商定義為一階差商的差商：

一般地，n 階差商遞推定義為：

為統一起見，補充定義函數f(x1)為零階差商。

一般地，用數學歸納法易證：

2.4 差商形式的插值形式

這種差商形式的插值公式稱作牛頓插值公式，牛頓公式其實只是拉格朗日公式的一種變形[6-7]。

3 Hermite 插值法

1.在某些問題中，為了保證插值函數能更好與原來的函數重合，使插值函數更接近原來函數軌跡，不但要求“過點”，即兩者在節點上具有相同的函數值，而且要求“相切”，即在節點上還具有相同的導數值，這類插值稱作切觸插值，或稱埃爾米特（Hermite）插值。顯然，埃爾米特插值是泰勒插值和拉格朗日插值的綜合和推廣。

2.Hermite 插值基本原理。通常如上條件的Hermite型插值是通過構造相應的插值基函數來完成的，為方便起見，以n=1 為例，說明傳統的求解方法，設給定的x0,x1和相應的函數值f(x0),f(x1)及微商值f'(x0),f'(x1)構造插值函數H3(x)。由構造函數的辦法可知：對應于x0和x1點函數值的插值函數分別為：

而對應的x0和x1點導數值的插值基函數分別為：

因此所要求的插值函數H3(x)=f(x0)h0(x)+f(x1)h1(x)+f'(x0)H0(x)+f'(x1)H1(x)。

4 插值法的應用

加工零件的輪廓曲線：該問題是有一個待加工零件，它的外形根據工藝要求由一組數據（x,y）給出（在平面情況下），要求要用數控機床加工時刀具必須沿這些數據點前進，并且由于刀具每次只能沿x 方向或y方向走非常小的一步，所以需要將已知數據加密，得到加工所要求的步長很小的（x,y）坐標。

表1 給出了輪廓線上x 每間隔0.2（長度單位）的加工坐標x,y（順時針方向為序，由輪廓線的左右對稱性，表中只給出右半部的數據），假設需要得到x 或y坐標每改變0.05 時的坐標，試完成加工所需的加密數據，畫出該零件的輪廓曲線。運用matlab 繪畫出的加工零件輪廓線，用不同的插值方法，畫出最好的效果圖。最后得出運用三次樣條插值，畫出的輪廓圖最好。

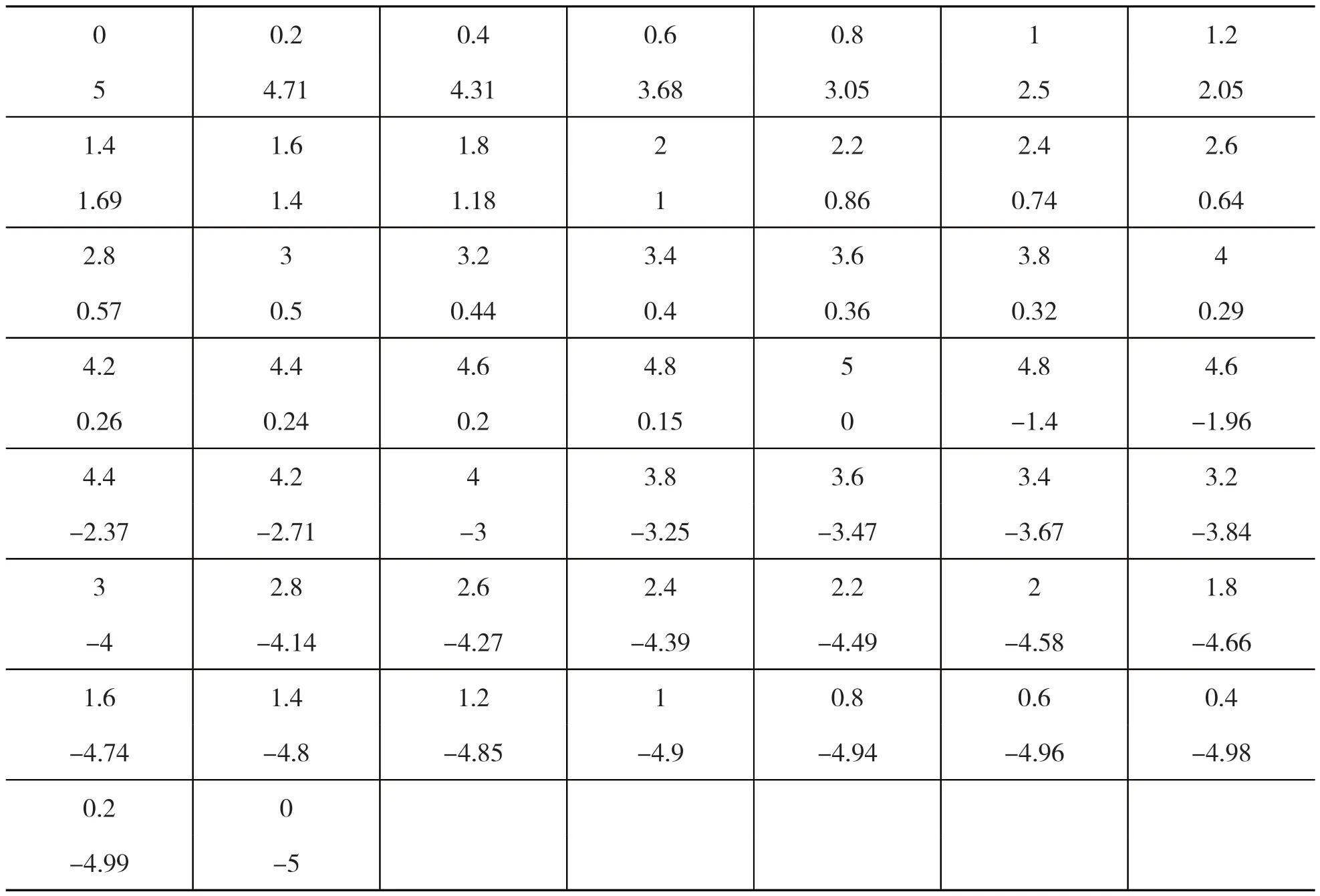
表1 x 間隔0.2 的加工坐標（x,y）（右半部的數據）

5 結語

我們通過對函數插值的分析及研究，用解決實際問題的方法，對不同的插值方法都有了深刻的了解，并掌握了運用matlab 解決插值問題，明白了各個插值方法的含義。這讓我們不僅僅局限于理論知識的理解，更上升到了實際問題中，加深了我們對于插值函數的認識。