紋理異常感知SAR自監督學習干擾抑制方法

韓朝赟 岑 熙 崔嘉禾 李亞超* 張 鵬

①(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)

②(中國科學院微小衛星創新研究院 上海 201314)

1 引言

合成孔徑雷達(Synthetic Aperture Radar,SAR)作為一種重要的探測系統，能夠實現對目標場景進行高分辨成像，在民用和軍用領域具有廣泛的應用[1,2]。然而，在當前日趨復雜的電磁干擾環境下，針對合成孔徑雷達研究的干擾方法日益多樣[3]，已嚴重制約了合成孔徑雷達的工作性能。因此，開展合成孔徑雷達干擾抑制技術研究顯得越來越迫切。

現有主流合成孔徑雷達干擾抑制方法按照技術途徑，可劃分為非參數化、參數化以及半參數化干擾抑制方法[4]。非參數化方法主要適用于強干擾情況，且需要進行干擾判決，主要分為陷波濾波器、自適應濾波器和子空間投影方法。陷波濾波器和自適應濾波器方法通過在信號頻域[5]或時頻域[6]構建濾波器來實現對強干擾主瓣的抑制，如文獻[5]提出了一種自適應檢測方法對干擾進行定位，并據此確定濾波器帶寬，從而實現對窄帶干擾的抑制。但陷波/自適應濾波器在抑制干擾時，都不可避免地導致部分回波信號的損失。基于子空間投影的抗干擾方法[7,8]試圖構建相互正交的信號子空間和干擾子空間，利用雷達回波信號在干擾子空間的投影實現對干擾的分離，如文獻[9]提出的基于時頻域的子空間投影方法，可有效對抗窄/寬帶壓制干擾，但該類方法的子空間相互正交假設對截取-轉發的間歇采樣轉發等有源相參壓制干擾效果有限，且具有較高的計算復雜度。參數化[10-12]與半參數化[13-15]方法的思路類似，通過構建干擾的半參數/參數化模型，并利用優化理論求解其模型參數，從而實現干擾的提取和分離。文獻[13]提出一種基于稀疏重構理論的半參數化抗干擾方法，其分別構建的SAR信號和干擾信號的稀疏字典，完成優化建模，并采用稀疏重構優化求解目標和干擾信號模型參數，實現信干分離。然而，參數化方法存在計算復雜度高、模型依賴干擾先驗等缺陷，在面對干擾類型變化多樣、調制方法復雜的干擾情況，其抗干擾效果有待提升。

近些年，深度學習憑借對結構化數據進行特征提取方面的優勢，已在諸多領域獲得了廣泛應用。目前，深度學習在抗干擾領域的應用主要集中于干擾類型的識別[16-19]，而直接將深度學習應用于干擾抑制處理的嘗試則較少。文獻[20]提出了一種基于分類網絡的干擾判決方法，并試圖基于干擾先驗，構建一個卷積神經網絡模型來實現干擾抑制。文獻[21]將生成對抗網絡應用到上述網絡模型的構建中，實現干擾抑制性能提升；文獻[22,23]則分別提出一維卷積神經網絡和門控循環單元(Gated Recurrent Unit,GRU)模型，實現時域干擾抑制，訓練網絡學習將受到干擾的回波映射至干凈的回波。然而，上述基于深度學習的干擾抑制方法均簡單采用“端-端”方式，使用匹配的干擾-無干擾數據對神經網絡進行監督訓練，而忽略了現實中不同干擾能量強度的隨機性。這時，不同干信比下回波信號歸一化后數值分布差異大，難以有效完成干擾-無干擾的映射學習，不具有實用性。此外，監督學習訓練的神經網絡模型依賴于干擾先驗，僅能夠對抗訓練集內的干擾類型，缺乏泛化性；若引入更多干擾類型，則需要提升網絡模型容量，使得模型訓練難度增大，計算復雜度隨之提高。

針對上述方法存在的問題，本文提出了一種基于紋理異常感知的SAR自監督干擾抑制方法：(1)針對干擾類型復雜多樣、現有方法依賴干擾先驗問題，本文依據干擾的時頻紋理異常，基于自監督學習構建干擾時頻定位網絡模型Location-Net實現干擾信號的時頻定位與抑制，從而使得方法具有較強的泛化性，保證抗干擾類型多樣；(2)針對目標與干擾信號時頻譜重疊而導致的信號損失問題，構建了一種信號修復網絡模型Recovery-Net對缺失的目標信號進行修復。仿真和實測數據抗干擾結果表明了本文所提方法的有效性。同時考慮到實時性，將本文方法與主流輕量化卷積神經網絡的計算復雜度進行了對比。

2 基于紋理異常感知的干擾抑制原理

2.1 典型SAR干擾的時頻聚集特性分析

對于受到干擾的合成孔徑雷達，其接收脈沖回波由目標回波信號、干擾信號以及背景噪聲3部分構成：

其中，n為時間采樣點，s(n)表 示目標回波信號，i(n)表示雷達接收到的干擾信號，ω(n)表示背景噪聲。對于干擾信號i(n)的構成，典型強脈沖式干擾、窄帶壓制干擾、調頻寬帶壓制干擾等不同類型干擾具有不同的調制方式，但在局部時間窗內，都可近似為寬/窄帶調頻干擾。這時，干擾信號模型可以表示為復雜寬/窄帶調頻干擾的組合：

其中，l為干擾段編號，gτ(n-nl)為 中心位置nl，寬度τ的矩形窗函數，Al為第l段干擾的幅度，φl(n)為第l段干擾的頻率調制。在任意瞬時時刻，式(2)中干擾頻率取值單一且隨時間變化。因此，這時將r(n)轉化到時頻域進行分析，可得其時頻譜R(n,k)

其中，k為頻率采樣點，w(m-n)為以n為中心的滑窗，L為滑窗窗長，S(n,k)為目標回波時頻譜，I(n,k)為干擾時頻譜，Ω(n,k)為背景噪聲時頻譜。對于n0時刻的瞬時譜R(n0,k)，干擾瞬時譜I(n0,k)為 干擾信號在滑窗w(m-n0)內的頻譜，頻率范圍較窄，干擾瞬時譜I(n0,k)在R(n0,k)中覆蓋范圍較小，與目標回波瞬時譜S(n0,k)重合度低，使得干擾在時頻譜內呈現出較強的聚集性。如圖1所示，分別列舉了間歇采樣轉發干擾、非均勻間歇采樣轉發干擾、線性函數移頻干擾下實測SAR脈沖回波數據時/頻/時頻圖。圖1(a)-圖1(c)分別對應于3組受干擾信號的時域波形，圖1(d)-圖1(f)分別對應于3組受干擾信號頻譜。顯然，時域與頻域中回波信號均受到干擾的大范圍覆蓋，難以分辨。然而，觀察圖1(g)-圖1(i)所對應的時頻譜圖，發現干擾能量離散分布于一系列瞬時譜中，其中每一瞬時譜內的干擾頻率范圍小，即二維時頻譜內干擾的聚集性強。這時，目標與干擾信號重合度較低，干擾呈現出可分離性。因此可利用該特性開展SAR有源干擾抑制方法研究。

圖1 間歇采樣轉發/非均勻間歇采樣轉發/線性函數移頻干擾的多域特性圖Fig.1 Multi-domain of interrupted-sampling and repeater jamming/heterogeneous interrupted-sampling and repeater jamming/linear function frequency shift jamming

2.2 干擾抑制與信號修復

根據2.1節分析可知，強脈沖式有源主瓣干擾類型在時頻域中呈現出較強的聚集性，且干擾時頻分量僅局部存在于回波時頻譜中，大部分目標回波時頻分量不受干擾影響。此外，實際中干擾類型/幅度多樣，特征分布各不相同，紋理特征差異較大，但正常雷達回波分布與紋理特征則相對穩定。因此，基于這一特性，考慮卷積神經網絡對結構化數據的局部紋理特征的提取能力，構建卷積神經網絡模型學習正常目標回波時頻譜Rc(n,k)的紋理特征分布Feature：

其中，models(·)為卷積神經網絡模型，Fc為網絡輸出的特征圖，Sc(n,k) 為Rc(n,k)中的回波時頻譜，Ωc(n,k)為Rc(n,k)噪聲時頻譜，Fc(n,k)為特征圖中(n,k)點的特征向量。這時，如果將受干擾雷達回波時頻譜Rj(n,k)輸入網絡進行運算：

其中，Sj(n,k),Ij(n,k),Ωj(n,k)分別為對應Rj(n,k)中的目標時頻譜、干擾時頻譜和噪聲時頻譜。則對于Rj(n,k)中異于正常回波紋理的干擾部分而言，其特征提取結果將不屬于特征分布F eature：

因此，根據式(6)中神經網絡特征提取結果，可實現對時頻譜中干擾分量的檢測：

掩模 Mask(n,k)即為干擾時頻定位結果，其中0代表時頻譜對應位置中包含干擾，1代表不包含干擾，進而可通過 Mask(n,k)對接收回波時頻譜進行干擾抑制：

然而，由于實際目標回波信號時頻譜Sj(n,k)與干擾時頻譜Ij(n,k)存在部分重疊，經式(10)處理后，將使得部分目標回波信號也會受到掩模Mask(n,k)抑制，造成目標信息損失，因而需要對其進行損失修復。從原理出發，目標回波可以理解為目標場景對發射信號的調制，部分回波信號損失并不會導致目標信息的完全丟失。因此，根據受損回波時頻特性，可考慮利用訓練神經網絡模型來提取目標特征信息，從而預測完整回波的時頻譜：

其中，modelr(·)為用于損失信號修復的神經網絡模型，(n,k)為修復后的回波信號時頻譜。經神經網絡模型修復后，通過時頻變換(本文采用短時傅里葉逆變換(Inverse Short Time Fourier Transform,ISTFT))可將修復后的回波變換到時域，即(n)。然而，ISTFT對時頻譜進行的二維滑窗加權求和處理，其本質是僅沿時間維滑動的二維卷積層運算過程。因此，對于滑窗窗長為L的ISTFT處理，其變換過程可以寫為時頻譜與L×L卷積核的卷積：

其中，weightL×L表示L×L卷積核，?代表卷積運算，convL×L(·)表示L×L卷積層。這時，回波信號的時頻譜修復與ISTFT過程可寫為

顯然，由于卷積層 convL×L(·)與時頻譜修復神經網絡模型 modelr(·) 為串接關系，因而將c onvL×L(·)與modelr(·)融合，從而可直接構建神經網絡模型將損失回波時頻譜修復為完整時域回波信號：

從而直接將損失的回波時頻譜修復為完整時域回波信號：

注意，由于卷積層 convL×L(·)相對于回波時頻譜的感受野等同于卷積核形狀。所以，融合后的模型設計理應滿足感受野不小于L×L。

3 干擾抑制神經網絡模型

3.1 干擾時頻定位網絡模型(Location-Net)

根據2.2節分析可知，干擾時頻定位網絡特征提取作用于雷達回波的時頻譜，并且干擾時頻定位結果與輸入時頻譜保持相同分辨率，因此本文基于卷積自編碼器[24]設計了一種全新的干擾時頻定位網絡模型Location-Net，其利用對目標場景雷達回波時頻譜壓縮重構，依據重構誤差作為信號/干擾的區分特征。網絡模型訓練目標函數可寫為

對于雷達回波時頻譜中未受到干擾部分，其重構誤差較低；但對于受干擾部分而言，由于模型僅被訓練用于重構目標場景回波時頻譜的壓縮重構，因而其重構結果將會產生較大的誤差。所以通過對重構誤差設置閾值的方式即可完成對干擾分量的定位：

其中，L(n,k)為網絡模型的重構誤差模型，threshold為重構誤差閾值，其取值可根據模型對無干擾時頻譜的重構誤差計算獲得，誤差高于閾值部分為干擾時頻分量。

根據上述分析，本文設計的干擾時頻定位網絡模型Location-Net如圖2所示，網絡采用全卷積結構，共包含4層，每層的網絡參數如表1所示。網絡分為編碼/解碼器兩部分(編碼壓縮-解碼重建)，其中前兩層為模型的編碼器部分，用于對輸入網絡的時頻譜進行壓縮，采用3×3卷積層，卷積步長為2，并在卷積之后級聯批歸一化層(Batch Normalization,BN[25])和ReLU激活函數[26]；網絡后兩層為解碼部分，用于將時頻譜的壓縮結果進行重構，同樣采用3×3轉置卷積層實現上采樣，采樣步長為2。注意，網絡第3層卷積后級聯批歸一化層和ReLU激活函數，而第4層將前層的運算結果映射到網絡輸出的形式，卷積后不采用其他操作。此外，在網絡卷積前，需要對輸入進行寬度為1的補零，且由于批歸一化處理，所有卷積層均不設偏置項。

圖2 干擾時頻定位網絡模型(Location-Net)Fig.2 Interference time-frequency location network model (Location-Net)

表1 干擾時頻定位網絡參數Tab.1 Interference time-frequency location network parameter list

3.2 信號修復網絡模型(Recovery-Net)

相比干擾抑制，信號的損失修復常被學者所忽略。為解決這一問題，基于2.2節分析，本節設計了一種修復卷積神經網絡模型Recovery-Net實現損失信號的時頻域-時域修復的過程，其網絡模型整體呈現為一種收縮結構：網絡逐層計算過程中，輸入時頻譜的頻率維由32收縮至1，時間維則不進行大幅下采樣；同時，為保證輸入時頻譜邊緣數據能得到同等處理，網絡中所有卷積層不進行補零處理。因此，在網絡計算中，時頻譜特征圖的時間維長度將逐層減小。注意，由于本文默認STFT/ISTFT尺寸數為32，故網絡的感受野應不小于32×32。

基于上述分析，本文設計的修復網絡模型Recovery-Net如圖3所示，采用共包含7個卷積層的全卷積結構，各層參數如表2所示。網絡前3層均為5×5卷積層，其中前兩層沿頻率維卷積步長為2，其余卷積步長為1，使得前3層特征圖頻率維點數收縮至1；4至6層則需滿足網絡的時間維感受野，均為1×7卷積層，主要沿時間維進行特征提取和；第7層采用1×1卷積層，將前層計算結果映射至輸出時域回波形式。注意，除最后一層外，每個卷積層后級聯批歸一化層和ReLU激活函數，且所有卷積層均不設偏置項，卷積前也不進行補零。在信號修復過程中，各層計算得到的特征圖逐層減小，難以引入殘差連接[27]來避免網絡層數過多導致的模型退化問題。因此，修復網絡并未采用常見多個3×3卷積核代替大卷積層的網絡設計策略[28]，從而避免出現層數過多問題。

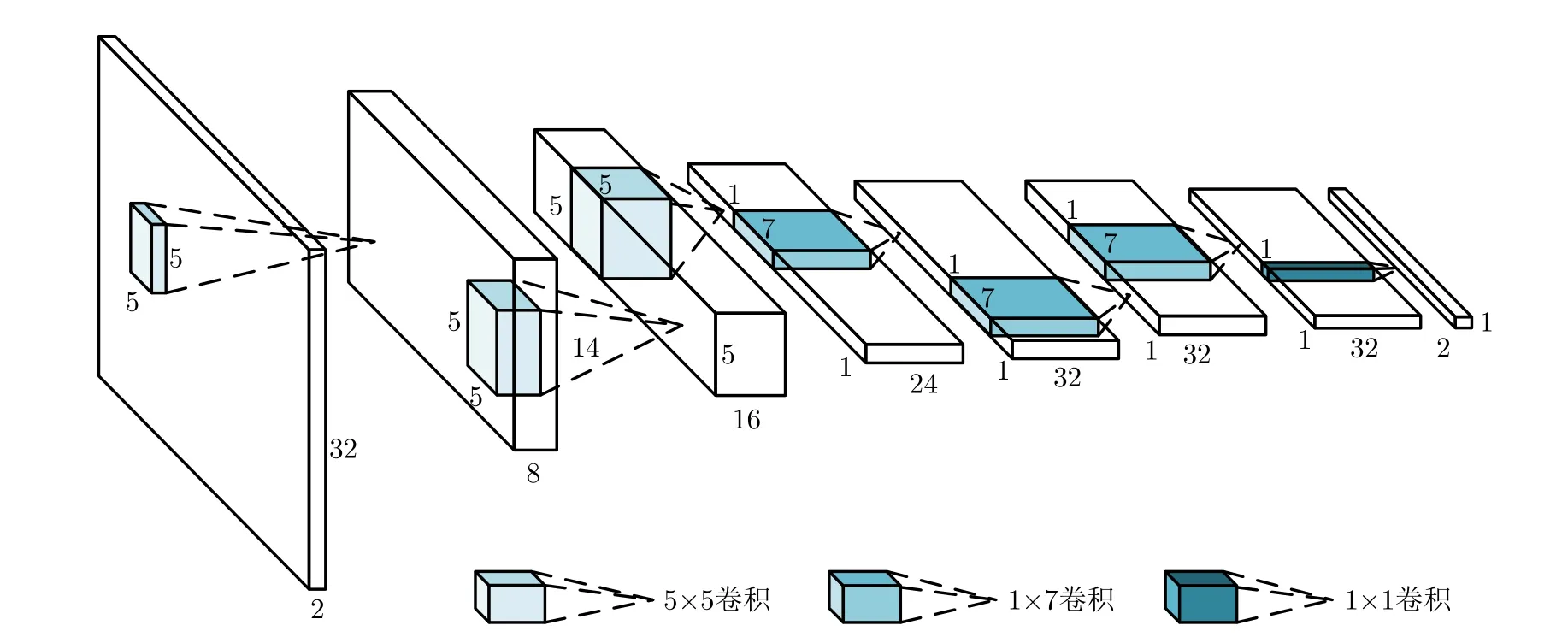
圖3 信號修復網絡模型(Recovery-Net)Fig.3 Signal recovery network model (Recovery-Net)

表2 基于卷積層的信號修復網絡參數Tab.2 Parameter list of signal recovery network based on convolution layers

3.3 網絡訓練數據與損失函數

由于干擾時頻定位與信號修復網絡模型均采用全卷積神經網絡模型，其本身對于輸入數據的時間長度并無限制，因而為方便后續批量化訓練，本文將默認采用相同時間維長度的訓練數據。此外，為配合干擾時頻定位和信號修復網絡模型訓練，對它們的損失函數也給出了明確定義，其中干擾時頻定位網絡模型的損失函數為MSE損失函數與SSIM損失函數[29]組合：

y為網絡模型的輸出，為對應的輸出標簽值。yi和分別為y和中的第i個值，μy和μ分別為y和的均值，σy和σ分別為y和的標準差，為y和的協方差，C1和C2為兩個常數項，用于避免分母接近0時的不穩定。

而信號修復網絡模型僅采用MSE損失函數作為訓練的損失函數：

3.4 所提干擾抑制方法的總體流程

綜上所述，本文所提的基于紋理異常的SAR自監督抗干擾方法處理框架主要分為兩個部分，其總體流程框架如圖4所示：(1)訓練干擾時頻定位神經網絡模型Location-Net學習無干擾回波時頻譜的深度特征分布，以實現對受干擾回波時頻譜中干擾分量的異常檢測和定位抑制；(2)訓練修復神經網絡模型Recovery-Net，并以(1)中處理結果為輸入，完成損失時域回波的修復。然而，值得注意的是，修復神經網絡模型的設計受ISTFT參數影響，在后續處理中，默認參數為：窗函數為窗長為31的漢明窗，傅里葉變換點數設為32，窗的滑動步長為1。同時，由于實際中輸入雷達回波的干信比不定，為保證不同數據相對于網絡模型的一致性，定義歸一化尺度為

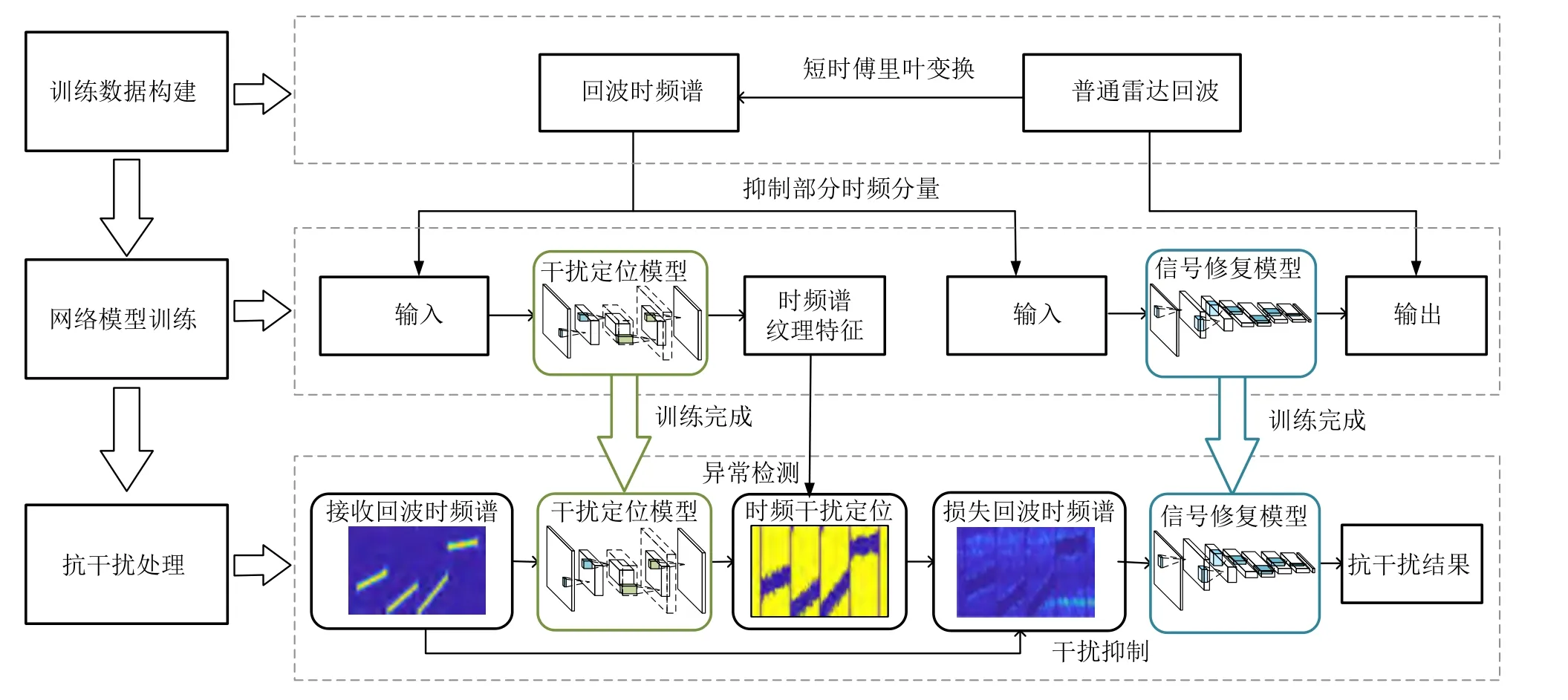
圖4 基于自監督學習的干擾抑制流程Fig.4 Interference suppression process based on self-supervised learning

其中，R為雷達回波的斜距，vmax為訓練數據中的最大值，R0為vmax所屬雷達回波的斜距。使用歸一化尺度對神經網絡輸入數據進行歸一化，以減小不同雷達回波間幅度分布的差異性。最后，在第4節將通過仿真與實測數據來具體實現和驗證方法的有效性。

4 實驗結果分析

首先，為保證本文方法的真實可復現以及有效性，給出試驗環境配置：處理器為Intel(R) Core(TM) i7-10700，內存為64 GB，顯卡為GeForce RTX 3090 。實驗使用Pytorch深度學習框架[30]實現網絡模型及其訓練和推理算法。干擾時頻定位網絡模型和信號修復網絡模型采用相同的訓練策略：使用Adam優化算法[31]作為網絡訓練算法，訓練批次(batch)為64，總訓練周期(epoch)為20，初始學習率為0.0001。當訓練進行至第16個周期時，固定網絡中的所有批歸一化層參數不再更新，并將學習率減小10倍。

同時，為評估抗干擾性能，文本使用干擾抑制比(Interference Suppression Ratio,ISR)[7]、信號失真比(Signal-to-Distortion Ratio,SDR)[32]、乘性噪聲比(Multiplicative Noise Ratio,MNR)[9]、余弦相似度(Cosine Similarity,CS)、結構相似性(Structural Similarity,SSIM)[29]作為評價標準。

其中，干擾抑制比，即信號抗干擾前后的能量比，可有效反映算法抑制強干擾的能力，公式化模型為

其中，‖·‖F代表斐波那契范數，r代表受到干擾的雷達回波，代表抗干擾后雷達回波，干擾抑制比取值越大則干擾抑制能力越強。

信號失真比即無干擾的原信號與失真量的比率，用于評估抗干擾后的信號損失為

其中，s為對應于r的未受到干擾的雷達回波，信號失真比越高代表抗干擾中信號損失越小。

乘性噪聲比即弱散射區域和強散射區域的圖像強度的比率，用于評估SAR成像質量，其公式化模型為

其中，pm和M分別代表強散射區域的像素值和像素總數，pn和N分別代表弱散射區域的像素值和像素總數，乘性噪聲比取值越低則雷達圖像對比度越高。

余弦相似度通過計算兩個向量夾角的余弦值，以度量其相位相似性，其公式為

其中，Sc為 未加入干擾的原信號時頻譜，為采用抗干擾后回波信號時頻譜。余弦相似度取值范圍為[-1,1]，其取值越高代表兩個向量的相位越接近。

結構相似性(SSIM)通過亮度、對比度和結構的差異評估兩幅圖像局部紋理的相似度，其式為

其中，x和y分別為進行對比的兩幅圖像，μx和μy分別為圖像亮度均值，σx和σy分別為圖像亮度方差，σxy為兩幅圖像亮度的協方差，C1和C2為兩個常數項。SSIM越接近1兩幅圖像越相似。下面將分別基于仿真與實測數據來驗證所提方法的有效性。

4.1 仿真干擾數據抗干擾結果分析

為驗證本文所提方法對受干擾SAR回波的抗干擾能力，本節在實測SAR回波基礎上，添加線性函數移頻干擾仿真干擾，干擾信號表示為[33]

其中，T為干擾脈沖寬度，f0為中頻線性調頻信號的中心頻率，K為中頻線性調頻信號的調頻率，fj為 線性函數移頻干擾信號的初始中心頻率，Kj為線性函數移頻干擾信號的初始調頻斜率。實測SAR回波數據的雷達系統參數如表3所示。

表3 加入仿真干擾的實測SAR回波參數Tab.3 Parameters of measured SAR echo with simulated jamming

為仔細觀察其處理效果，取任一脈沖回波的時頻域處理結果進行評估，結果如圖5所示。其中，圖5(a)，圖5(b)分別為無干擾/加入仿真干擾的回波時頻域譜圖，可清晰地發現在存在多個幅度、中心頻率和調頻率各異的干擾脈沖情況下，真實回波被完全淹沒。經所提方法預處理，并輸入干擾時頻定位網絡Location-Net后，得到如圖5(c)所示的時頻譜壓縮重構結果，對比圖5(a)和圖5(b)，未受到干擾的部分重構誤差較小，而干擾部分整體呈現缺失，重構誤差較大。根據圖5(b)和圖5(c)的重構誤差，按照式(17)得到的干擾時頻定位掩模如圖5(d)所示，其中藍色部分代表受到干擾的時頻分量，黃色部分代表未受到干擾時頻分量，其中時頻譜中主要干擾時頻分量均被定位，同時不同干擾段交界處產生的頻譜展寬分量也被定位。然后基于該掩模，按照式(9)進行干擾抑制，圖5(e)即為干擾抑制的結果，干擾的主要時頻分量被抑制。最后使用信號修復網絡模型Recovery-Net對干擾抑制后的回波時頻譜進行修復，圖5(f)為修復后回波的時頻譜，可以看到對應圖5(e)中缺損的時頻分量已得到一定程度修復。

圖5 本文方法處理各階段時頻域Fig.5 Time-frequency of echo stage during processing by our method

為進一步觀察信號損失修復效果，圖6給出了干擾抑制前后的單脈沖的時域對比。圖6(a)和圖6(b)分別給出原始回波和添加干擾后的回波時域圖，干擾整體呈現恒模、切片離散分布的特點，其干信比分別為30 dB和20 dB。圖6(c)和圖6(d)則給出了干擾抑制未修復/修復后的對比，從兩幅圖的結果看，很明顯干擾都得到了有效抑制，但圖6(c)中干擾區域的信號也受到了明顯的影響，而圖6(d)的修復結果基本與圖6(a)相似，驗證了所提方法的有效性以及信號損失修復問題的必要性。

圖6 抗干擾前后雷達回波對比Fig.6 Comparison of radar echo before and after anti-jamming

由于SAR成像過程對相位信息敏感，對信號修復后雷達回波相位恢復精度進行評估。本文使用余弦相似度評估抗干擾后信號的相位誤差。圖7給出了信號修復后回波時頻譜與未加入干擾的原信號時頻譜間的余弦相似度，其中顏色越淺(黃色部分)余弦相似度越接近1，即相位誤差越接近0；而顏色越深(深藍色部分)余弦相似度越接近-1，即相位誤差越接近π。對應圖5(b)，未受到干擾的部分余弦相似度較高，其相位基本與原信號一致；而對于受到干擾的部分，圖7中多數時頻點的余弦相似度高于0，部分區域的余弦相似度接近1，相位接近原信號，同時也存在少數相位誤差較大的時頻點，但其時頻空間分布較為分散。整體上，經本文信號修復網絡處理后，回波相位信息得到一定恢復。

圖7 信號修復后雷達回波相位誤差Fig.7 Phase error in radar echo after signal recovering

為了體現本文所提算法優勢，采用3種現有典型抗干擾方法(IALM方法[13]、ESP方法[7]、時頻陷波濾波器[6])對表3數據進行抗干擾處理，并與本文所提算法結果進行對比。

如圖8所示，圖8(a)為使用IALM方法進行干擾抑制后的回波時頻譜，對比圖5(a)中的原信號，該處理結果雖然干擾信號得到大幅抑制，但回波信號能量整體受到較大的損失。圖8(b)為使用ESP方法進行干擾抑制后的回波時頻譜，由于干擾的中心頻率和調頻率的變化，干擾在頻域覆蓋范圍極高，導致ESP方法難以構建出完備的干擾子空間，因此圖8(b)中僅有部分干擾所在頻率分量受到抑制。圖8(c)為使用陷波濾波器進行干擾抑制后的回波時頻譜，對比圖5(b)中原干擾信號，其干擾的主要部分已得到抑制，但能量相對更弱的干擾頻譜展寬分量則沒有被抑制，其能量仍對目標場景回波形成壓制。

圖8 現有方法抗干擾處理后回波時頻域Fig.8 Time-frequency of echo stage after processing by existing anti-jamming method

最后，從干擾抑制與修復后的SAR成像結果評估所提方法的抗干擾性能，并與現有抗干擾方法處理結果進行對比。如圖9所示，圖9(a)和圖9(b)分別為原始SAR圖像和受干擾SAR圖像，其中場景完全被強干擾信號覆蓋；而圖9(c)和圖9(d)分別為本文方法的干擾抑制和抑制+修復圖像結果，修復后圖中紅色和橙色框線內圖像得到增強；圖9(e)為使用IALM方法進行干擾抑制后的成像結果，圖中干擾基本得到抑制，目標場景顯現，但圖像信噪比明顯弱于圖9(d)；圖9(f)，圖9(g)分別為使用ESP方法和陷波濾波器方法進行干擾抑制后的成像結果，圖中干擾對目標場景的覆蓋情況仍十分嚴重。對于各方法的定量分析結果，表4列出了本文算法與對比方法的干擾抑制比ISR、信號失真比SDR，以及成像結果與未受到干擾回波的成像結果圖9(a)的結構相似性SSIM。其中，對于IALM方法，其較高的ISR源于對目標信號的抑制，同時也導致了SDR值較低，信號失真程度較高；對于ESP方法，其對于本節數據的處理效果較差；對于陷波濾波器方法，其干擾抑制能力不足；而經本文所提干擾抑制后，具有更為優異的抗干擾性能指標，并在信號修復后得到進一步提升，體現了本文算法的優勢。

表4 仿真干擾數據抗干擾評估Tab.4 Anti-jamming evaluation of data with simulate interference

圖9 仿真干擾數據抗干擾成像結果對比Fig.9 Comparison of imaging result of data with simulated interference after anti-jamming

4.2 實測多類型干擾數據抗干擾實驗分析

在4.1節基礎上，利用實測干擾數據來進一步分析所提方法的有效性，并與現有抗干擾方法(IALM方法[13]、ESP方法[7]、時頻陷波濾波器[6])進行對比，驗證所提方法對多類型干擾的泛化性能，所用實測雷達系統參數如表5所示。

表5 實測數據雷達參數Tab.5 Radar parameters of measured data

4.2.1 相參壓制干擾

首先，測試所提方法對實測相參壓制式干擾抑制性能分析和對比。圖10(a)為實測受干擾SAR脈沖回波時頻譜，干擾在時域全覆蓋，同時干擾在時間維的不連續造成時頻譜中存在大量的干擾頻譜展寬分量。圖10(b)為采用IALM方法進行干擾抑制后的回波時頻譜，其中時頻域主要干擾頻率分量基本得到抑制，但時頻譜中仍殘留大量的頻譜展寬分量對回波數據造成一定的遮蓋。圖10(c)為使用ESP方法進行干擾抑制后的回波時頻譜，ESP算法根據回波信號的構成，主要對干擾所在頻段的信號進行了大幅抑制。圖10(d)為使用陷波濾波器進行干擾抑制后的回波時頻譜，由于時頻譜中頻譜展寬分量較多，導致整體能量幅度較高，使得基于統計假設檢驗的陷波濾波器方法主要適用于強干擾，對數據中干擾的時頻定位區域較少，干擾及其頻譜展寬量殘留較多。圖10(e)為使用本文所提方法進行抗干擾處理后的回波時頻譜，其中干擾基本得到濾除，損失信號得到一定程度修復。

圖10 實測相參壓制干擾抗干擾時頻域Fig.10 Time-frequency spectrum of measured data with coherent suppression jamming after anti-jamming

抑制后成像結果如圖11所示。圖11(a)中原始圖像受到相參壓制式干擾影響，目標場景被完全淹沒。圖11(b)-圖11(d)分別為采用IALM方法、ESP方法和陷波濾波器進行抗干擾處理后SAR成像結果，其中仍包含大量干擾殘留，影響對圖像的分辨能力。圖11(e)為使用本文方法進行抗干擾處理后SAR成像結果，干擾基本被濾除。

圖11 實測相參壓制干擾抗干擾成像結果Fig.11 Imaging result of measured data with coherent suppression jamming after anti-jamming

最后，表6給出了現有方法和所提方法的定量化對比結果，本文所提方法的干擾抑制比相較于IALM方法提升4 dB，相較于ESP方法提升10.27 dB，而相較于陷波濾波器提升5.39 dB，干擾抑制能力更強，成像對比度更高，目標場景更清晰。

表6 實測相參壓制干擾數據抗干擾評估Tab.6 Anti-jamming evaluation of measured data with coherent suppression jamming

4.2.2 相參運動多假目標干擾

針對相參運動多假目標欺騙干擾，同樣采用所提方法、IALM方法、ESP方法以及基于時頻陷波濾波器抗干擾方法進行干擾抑制性能分析和對比。圖12(a)為實測相參運動多假目標欺騙干擾的SAR脈沖回波時頻譜，圖中存在5個假目標的線性調頻干擾信號。圖12(b)為使用IALM方法進行抗干擾處理后回波時頻譜，干擾時頻分量被削弱但并未完全得到抑制，其能量依舊對回波數據形成壓制。圖12(c)為使用ESP方法進行抗干擾處理后回波時頻譜，算法對時頻譜中強干擾所在的頻段進行了抑制，造成大量的回波信息損失，同時干擾中較弱的頻率分量并未完全得到抑制。圖12(d)為使用陷波濾波器進行抗干擾處理后的回波時頻譜，由于圖中干擾的時頻分量存在兩種能量，陷波濾波器僅完成對其中較強的干擾進行抑制，濾波效果欠佳。圖12(e)為使用本文方法進行抗干擾處理后的回波時頻譜，干擾基本被濾除，而且同頻段信號分量也得到一定的修復，整體呈現出近似原始信號的時頻譜圖像。

圖12 實測相參運動多假目標干擾抗干擾時頻域Fig.12 Time-frequency spectrum of measured data with coherent motion and multi-false target interference after anti-jamming

圖13給出了實測相參運動多假目標干擾抑制后的SAR成像結果，其中圖13(a)為實測受到相參運動多假目標干擾的SAR成像結果，圖中出現5×5高能量假目標點區域，同時假目標干擾的運動調制造成圖中方位向壓制線，目標場景完全被淹沒；圖13(b)-圖13(d)則分別對應于IALM方法、ESP方法和陷波濾波器干擾抑制后的SAR成像結果，它們均未能有效抑制干擾，目標場景被干擾覆蓋；圖13(e)為使用本文方法進行抗干擾后SAR成像結果，干擾基本得到抑制，目標場景整體顯現，但處理后圖像信噪比有所下降。

圖13 實測相參運動假目標干擾抗干擾成像結果Fig.13 Imaging result of measured data with coherent motion and multi-false target interference after anti-jamming

表7定量化對比了3種方法以及所提方法的抗干擾效果，相較于IALM方法，本文方法干擾抑制比提升2.14 dB；相比于ESP方法，本文方法干擾抑制比提升4.84 dB；相比于陷波濾波器，干擾抑制比提升2.97 dB。對于成像結果的評估中，由于對比方法處理結果中未能有效抑制干擾，干擾使得圖像的對比更強烈導致MNR值更低。

表7 實測相參運動假目標干擾數據抗干擾評估Tab.7 Anti-jamming evaluation of measured data with coherent motion and multi-false target interference

4.2.3 組合式干擾

最后，面向未來組合式干擾發展趨勢，考慮實測相參壓制式與相參運動多假目標組合干擾場景，并依然采用IALM方法、ESP方法和陷波濾波器進行對比。圖14(a)為實測組合式干擾下SAR脈沖回波時頻譜，圖中相參壓制干擾和多假目標干擾交替出現(該實測SAR回波數據中存在其他僅受到相參壓制干擾或相參運動多假目標干擾的脈沖回波)。圖14(b)由于干擾的調制方式較為復雜，而IALM方法干擾模型相對簡單，難以應對復合干擾，因此干擾并未完全被抑制。而圖14(c)中，ESP方法對干擾所在的主要頻率分量進行抑制，導致雷達回波信息損失，部分干擾以及干擾的頻譜展寬分量未受到抑制。圖14(d)中，陷波濾波器對干擾較強的時頻分量進行了抑制，而由于干擾頻譜展寬量的能量相對較弱，因此并未受到抑制。最后，圖14(e)為使用本文方法進行抗干擾處理后的回波時頻譜，回波時頻譜中干擾的主要分量基本得到抑制。

圖14 實測復合干擾抗干擾處理時頻域Fig.14 Time-frequency spectrum of measured data with complex interference after anti-jamming

相對應，圖15給出了實測組合式干擾抑制后的SAR成像結果，圖15(a)中相參運動假目標干擾和窄帶相參壓制干擾組合形成了圖中多條較寬的方位向壓制帶，干擾的組合成像結果完全淹沒了目標場景；圖15(b)和圖15(c)分別為IALM方法和ESP方法進行抗干擾處理后SAR成像結果，其中兩幅圖像內的干擾能量均得到一定程度的抑制，但仍對目標場景形成壓制式干擾。圖15(d)為使用陷波濾波器進行抗干擾處理后SAR成像結果，圖像中目標場景基本顯現，但由于干擾未完全受到抑制，殘留的干擾導致圖像中包含較多噪聲，影響圖像的判讀。圖15(e)為使用本文方法進行抗干擾處理后SAR成像結果，圖像中兩類干擾都獲得了有效抑制，精確呈現出目標場景。

圖15 實測組合式干擾抗干擾處理成像結果Fig.15 Imaging result of measured data with complex interference after anti-jamming

表8對抗干擾效果進行了定量化分析，對于干擾抑制能力的評估，本文所提方法干擾抑制比相較于IALM方法提升2.04 dB，相較于ESP方法提升4.17 dB，相較于陷波濾波器提升1.44 dB。對于成像結果的評估中，由于IALM和ESP方法均未能完全抑制干擾，成像結果中存在的干擾使得其MNR值較低；而陷波濾波器處理后圖像信噪比較低，其MNR值高于所提方法。因此，通過上述試驗分析可知，所提方法不僅干擾抑制性能更為優秀，而且克服干擾先驗的同時，具備較好的泛化能力。

表8 實測組合式干擾數據抗干擾評估Tab.8 Anti-jamming evaluation of measured data with complex interference

4.3 模型復雜度分析

神經網絡模型的復雜度主要取決于浮點運算量和內存訪問量。對于卷積層，如果該層輸入形狀為Cin×Win×Hin，輸出形狀為Cout×Wout×Hout，卷積核形狀為K×K，則其浮點運算量(Floatingpoint Operations,FLOPs)為

該層的參數量為

運算所需的內存訪問量(Memory Access Cost,MAC)為

在相同的網絡輸入形狀(2×32×1024)下，對本文所提干擾時頻定位網絡Location-Net與信號修復網絡Recovery-Net組合模型、現有合成孔徑雷達抗干擾神經網絡模型IDN和IMN組合模型[20]以及主流輕量化主干網絡MobileNet V2[34]和ShuffleNet V2[35]的模型復雜度進行定量化對比(為了適應輸入形狀，這里將這兩個輕量化網絡略作修改：將網絡第1層輸入通道數改為2)，如表9所示。文獻[20]提出的兩種神經網絡模型：干擾檢測網絡IDN的設計源于VGG16網絡[28]，其網絡淺層的下采樣頻率低導致網絡中的13個卷積層均具有較高的浮點運算量，而網絡深層的3個全連接層使得網絡具有極高的參數量；干擾抑制網絡IMN中包含了遠超實際抗干擾需求的38個卷積層，且網絡中全程不使用下采樣操作，從而產生了巨大的運算量。因此，該方法的模型復雜度極高，對一個脈沖回波數據的抗干擾處理運算量極大，對于具有二維結構的合成孔徑雷達回波數據，處理效率低下。MobileNet V2和ShuffleNet V2是兩種現有主流輕量化主干網絡，其特征收縮式的網絡結構具有低計算量的優勢，被廣泛應用于當前的實時性任務中。本文所提的兩個網絡模型Location-Net(L-Net)與Recovery-Net(RNet)各項指標之和均優于這兩個輕量化網絡，具有一定的實時應用前景。

表9 神經網絡模型復雜度對比Tab.9 Comparison of neural network complexity

5 結語

本文提出了一種基于紋理異常的SAR自監督學習干擾抑制方法，依據干擾與信號回波在時頻域的紋理特征差異性及干擾信號的時頻聚集性，構建了一種干擾時頻定位神經網絡模型，實現了干擾信號的時頻定位，并在此基礎上進行干擾抑制。針對目標與干擾信號時頻譜重疊而導致的信號損失問題，構建了一種信號修復網絡模型對缺失的目標信號進行修復。仿真實驗和實測實驗結果驗證了本文所提方法對多種復雜有源主瓣干擾的有效性，以及對目標信號缺損信息修復的可靠性。此外，本文分析了所提方法的計算復雜度，結果表明該方法具備實際應用價值。最后，對于本文算法目前存在的一些局限性進行討論：首先，本文算法主要針對時頻域聚集性強的干擾類型進行干擾抑制，而對于時頻域分布較為彌散的干擾類型則難以對抗；其次，本文的兩個核心方法均還有改進的空間，可以通過改進網絡結構、訓練方法等進一步提升干擾時頻定位網絡對于正常樣本和異常樣本間的重構誤差差異，使得算法針對不同類型干擾的泛化性更強，以及提升信號修復網絡的修復精度，進一步減小信號損失。