風切變指數對風電機組輪轂高度選取的 影響分析

岳 俊，譙 剛，李文龍，汪志斌

(中國電建集團江西省電力建設有限公司，南昌 330000)

0 引言

隨著風電開發逐漸向中低風速區域轉移，有必要采取更多的技術手段來保證未來風電場在更低的風速條件下達到預期的收益。目前常用的技術手段主要有增加葉輪直徑、提升輪轂高度、改進控制策略、優化功率曲線、降低風電機組損耗等[1]，其中，增加葉輪直徑和提升輪轂高度兩種技術方法效果顯著。

在中國的中東南部低風速區域，提高風電機組塔筒高度對于提升風電場發電量，增加風電場收益具有顯著的作用。然而，風切變指數大小直接決定了塔筒高度，在不同的風電場，由于風切變指數不同，導致同一類型風電機組的塔筒即使提高相同高度，所增加的發電量也不相同[1]。一般情況下，風切變指數越大，風電機組發電量提升幅度越大，塔筒也就越高；風切變指數和塔筒高度、發電量基本成正比關系。隨著輪轂高度的提升，風速的增幅也在逐漸變小，導致風電機組發電量增幅也會隨著輪轂高度的提升而減少；同時輪轂高度的提升也帶來了塔筒重量、運輸、風電機組基礎、吊裝等相關成本和施工難度的增加。因此，風電機組塔筒高度提升帶來的發電量收益增幅的降低和工程投資成本增幅的變大，必然使風電機組輪轂高度存在一個平衡值，在這個平衡值上風電場將實現發電收益最大化[1]，同時這個平衡值也可以通過計算量化到風切變指數大小上。以往經驗認為，風切變指數在0.1～0.2時，可考慮選擇較高的輪轂高度；風切變指數大于0.2時，應選擇高輪轂高度。

隨著風電技術的不斷進步，以及輕量化的柔性塔筒技術的運用，使提升風電機組輪轂高度已經變得可行。當前的風電項目中，輪轂高度技術方案比選大多仍簡單的以靜態初始投資和年發電量的比值來計算風力發電的平準化度電成本(LCOE)，并以此作為風電機組輪轂高度的選取標準；但未從風電場全生命周期和經濟效益方面，對不同風電機組輪轂高度技術方案進行比選，缺乏一定的經濟性、合理性。

因此，有必要重新探討風切變指數與風電機組輪轂高度之間的內在關系。本文構建了一種新的風電機組輪轂高度選取模型，以財務凈現值作為動態分析不同輪轂高度技術方案比選的經濟指標，針對不同風切變指數的大小，選取合適的風電機組輪轂高度，從而實現風電場資源利用及收益的最大化。

1 風切變指數等級劃分

風切變是指風矢量在垂直方向上的空間變化。在一定高度范圍內，風速會隨著高度的上升而增大，風速隨高度的垂直變化叫做風切變。風切變指數越大，代表風速隨高度升高增加的幅度越大。在風資源評價領域，通常采用兩種數學關系式來描述測量得到的風切變指數：對數關系和冪指數關系[2]。

在GB/T 18710—2002《風電場風能資源評估方法》[3]中，規定了風切變指數公式為：

式中：V1和V0分別為高度在H1和H0處的風速；α為風切變指數。

風切變受地形和當地大氣熱力穩定度的影響，大氣熱力穩定度較高的地方更容易引起較大的風切變。同時，風切變指數受大氣熱力穩定度的影響嚴重，在中性(neutral)、穩定(stable)與不穩定(unstable)等不同大氣條件下，風廓線的變化很大。受地面粗糙度及地形的影響，不同地區的風切變指數是不同的；受大氣熱力穩定度的影響，即使同一地區，在不同時間段內風切變指數也不同[4]。在不考慮地形和地面粗糙度的情況下，風切變指數應該是夏、秋季偏低，冬、春季偏高[5]。山地地形由于受近地層大氣湍流的交換作用，近地層大氣熱力穩定度更加不穩定，會導致較小的風切變指數[5]。中國長江流域陰雨天氣較多，其日照時數與北方地區相比較少，且土壤濕度大，使得近地層大氣熱力穩定度較大，從而導致風切變指數較大。綜上所述，年均風切變指數呈現出山區小、平原地區大、沿海地區比平原地區稍小的特點[6]。

根據風切變指數范圍，結合國際對于風切變指數大小的定義，在中性大氣條件下，將風切變指數為1/7定義為適中(即標準風切變)，可把低空(一般定義為200 m以下)風切變指數等級分為5個等級[4]，具體如表1所示。

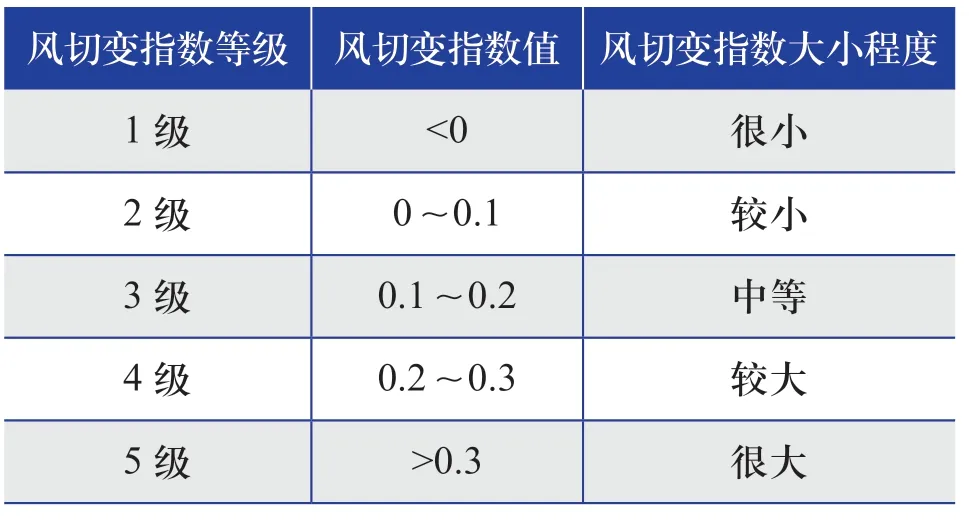
表1 低空風切變指數等級Table 1 Low altitude wind shear index level

2 風電機組輪轂高度選取模型

風電機組輪轂高度的提升使其發電量增加，同時也帶來了塔筒重量、運輸、風電機組基礎、吊裝等相關成本和施工難度的增加，最終會直接影響風電場的經濟效益。因此，選擇風電機組輪轂高度時，要分析增加輪轂高度獲得的發電量收益和增加的投資成本之間的關系，選擇經濟合理的風電機組輪轂高度[7]。

以往應用中，基于LCOE最低的風電機組輪轂高度選取方法運用比較多。LCOE的優點是作為機型比選的指標非常直觀，能用來比較不同輪轂高度下的風電機組全生命周期發電成本。但LCOE作為成本指標不能直觀反映項目的盈利能力，因此不能直接為企業提供投資決策[8]。另外，風電機組輪轂高度技術方案比選作為一種互斥方案的比較，內部收益率指標也只能用于衡量單方案的經濟性，而不能直接用于輪轂高度技術方案比選中，因此差額內部收益率、財務凈現值成為風電機組輪轂高度技術方案比選的優選指標。由于差額內部收益率在比選的互斥方案較多時需兩兩進行比較，計算較繁雜，也有可能出現差額內部收益率不存在的情況[9]，因此，財務凈現值法成為互斥方案比選時一種更簡單、更容易、更直接的方法。本文也以財務凈現值作為風電機組輪轂高度選取的經濟指標，接下來對模型構建方法進行介紹。

2.1 發電量計算模型

已知風速符合Webull分布，則風速頻率分布曲線函數f(v)[10]可表示為：

式中：k為形狀參數；c為尺度參數；v為風速。

設定風電機組的輸出功率曲線為P(v)，已知全年小時數為8760 h，根據風電場風速頻率分布和風電機組輸出功率曲線，可估算風電機組年理論發電量W，其公式為：

式中：Vin為風電機組切入風速；Vout為風電機組切出風速。

通過式(3)計算得到的風電機組發電量為理論值，沒有考慮尾流影響、廠用電和線損等電量損失，以及氣候變化、風電機組可利用率、功率曲線可利用率等不確定性因素對發電量的影響。所以風電機組實際發電量應該在理論發電量的基礎上乘以折減系數η，本文暫取0.7。

2.2 經濟評價模型

風電機組輪轂高度的提升主要帶來了塔筒、風電機組基礎和吊裝成本的增加，可把這部分增加的成本稱為增量成本I1。假定風電機組最低輪轂高度下的投資成本為初始投資成本I0，則相對于最低輪轂高度，較高輪轂高度下的總投資成本I可表示為：

綜合考慮目前國內風電機組制造水平、技術成熟度，以及商業化程度，以某風電機組廠家單臺額定功率為2500 kW的風電機組機型作為評價機型，該風電機組的技術參數如表2所示。

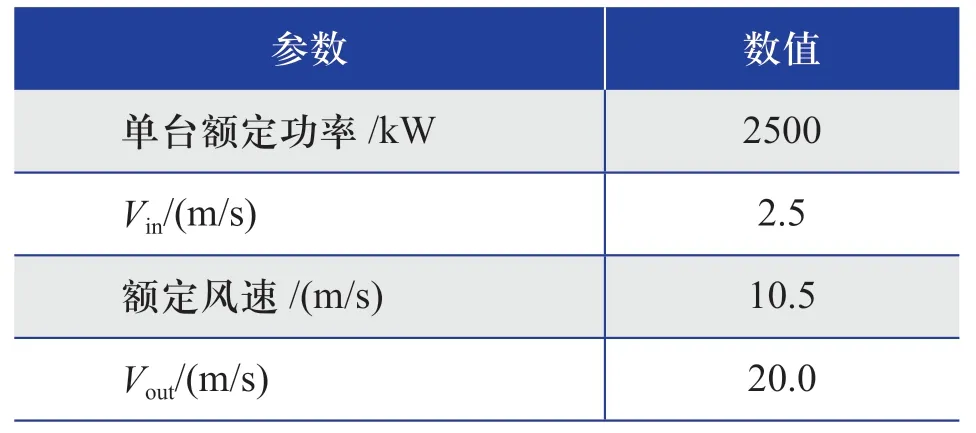
表2 作為評價機型的風電機組的技術參數Table 2 Technical parameters of wind turbine as evaluation model

根據風電機組廠家提供的該風電機組機型不同輪轂高度下的單臺塔筒重量和風電機組基礎用量，假定風電機組基礎形式為圓形擴展基礎，參考目前市場材料、設備價格水平和吊裝水平，可得到單臺風電機組不同輪轂高度下的塔筒、風電機組基礎和吊裝成本如表3所示。

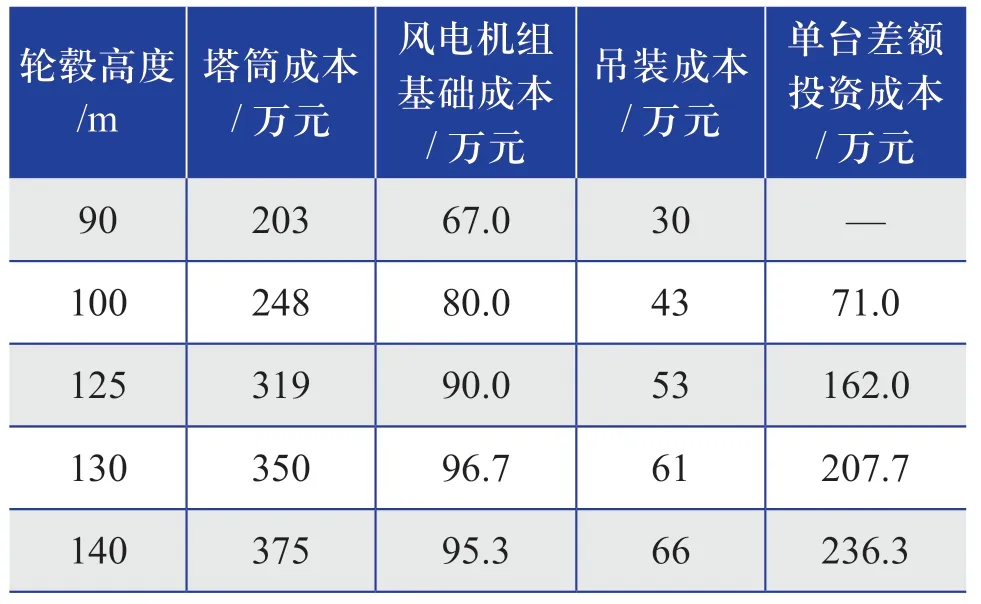
表3 單臺風電機組不同輪轂高度下的塔筒、 風電機組基礎、吊裝成本Table 3 Cost of tower drum，wind turbine foundation and hoisting of single wind turbine at different hub heights

參考《建設項目經濟評價方法與參數(第3版)》[11]，設定風電場運營期為20年，折舊年限為20年，殘值率為5%，資本金為20%，長期利率為4.9%，折現率為6%；風電場每年的運維成本按0.1元/W計算。以財務凈現值作為風電機組輪轂高度選取的評價指標，建立經濟評價模型。

3 不同風切變指數下風電機組輪轂高度的選取分析

3.1 不同風切變指數下輪轂高度處的風速變化

輪轂高度選取的關鍵是盡可能地增加風電機組發電量，使輪轂高度提升帶來的發電收益能夠抵消增加的投資成本，從而達到提高風電場經濟效益的目的。隨著風電機組輪轂高度的提升，輪轂高度處的風速也會隨之增加，但增加的速率逐漸減小。另外，相同高度處風速的增加率與風切變指數值有關，與平均風速的大小無關[12]。過往經驗認為，風切變指數小于0.1時，可選擇低輪轂高度；風切變指數在0.1～0.2時，可考慮選擇較高輪轂高度；風切變指數大于0.2時，可考慮選擇高輪轂高度。本文暫選取0.07～0.20之間的風切變指數作為研究對象，取值間隔為0.01，探討不同風切變指數下輪轂高度處的風速變化。

假定某風電場位于中國東部平原地區，90 m高度處的年均風速為5.5 m/s，空氣密度為1.225 kg/m3。根據風切變指數公式，可推算不同風切變指數下各輪轂高度處的年均風速，結果如表4所示。不同風切變指數下，年均風速隨輪轂高度的變化規律如圖1所示。

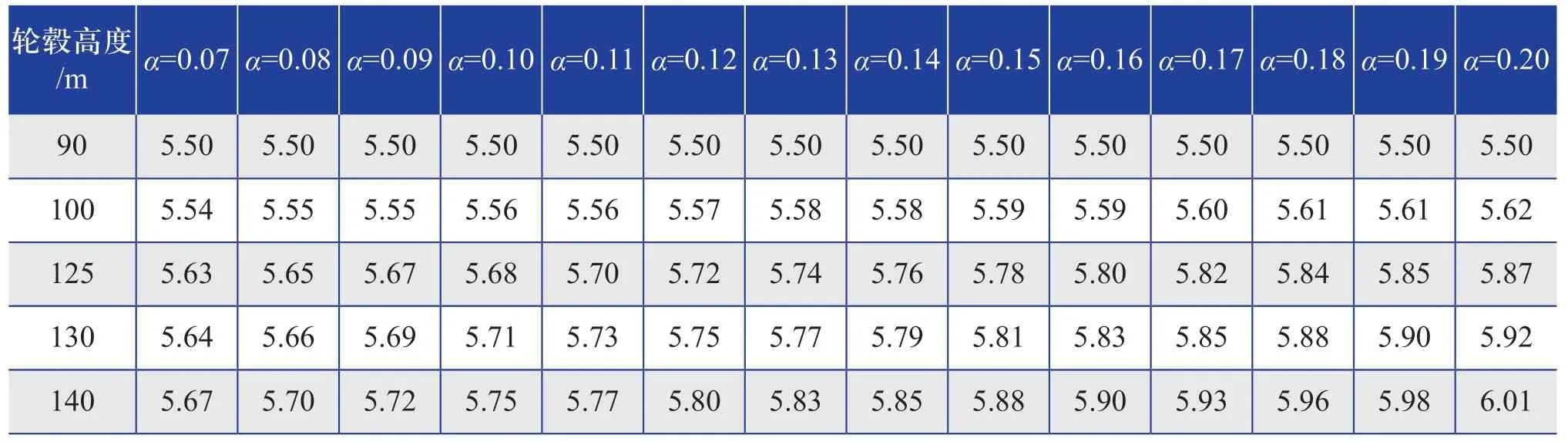
表4 不同風切變指數下各輪轂高度處的年均風速(單位：m/s)Table 4 Average annual wind speed at each hub height under different wind shear indexes(unit：m/s)

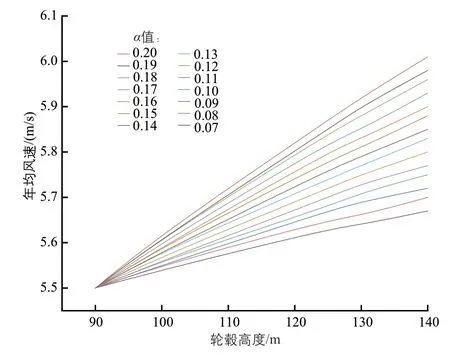
圖1 不同風切變指數下年均風速隨輪轂高度的變化規律Fig. 1 Variation rule of average annual wind speed with hub height under different wind shear indexes

由表4、圖1可以看出：年均風速隨著輪轂高度的升高而增加，但增加的速率呈現下降趨勢。風切變指數與年均風速增加的速率基本成正相關關系，風切變指數越大，年均風速隨輪轂高度升高而增加的速率就越快。

3.2 不同風切變指數下輪轂高度的選取

假定風電場裝機容量為50 MW，選用20臺2500 kW風電機組，參考目前工程建設成本水平，90 m最低輪轂高度時的單位千瓦建設成本為7000元/kW。根據風速的Webull分布，可計算不同風切變指數下不同輪轂高度時的風電場發電量和發電小時數。已知不同輪轂高度下塔筒、風電機組基礎、吊裝成本，可計算不同輪轂高度下的單位千瓦建設成本。

不同風切變指數下年發電小時數和單位千瓦建設成本隨輪轂高度的變化規律如圖2所示。需要說明的是，由于風切變指數過多，圖中僅顯示代表大、中、小風切變指數大小程度的0.20、0.14、0.07這3個風切變指數下的變化情況，后文圖3與此相同。

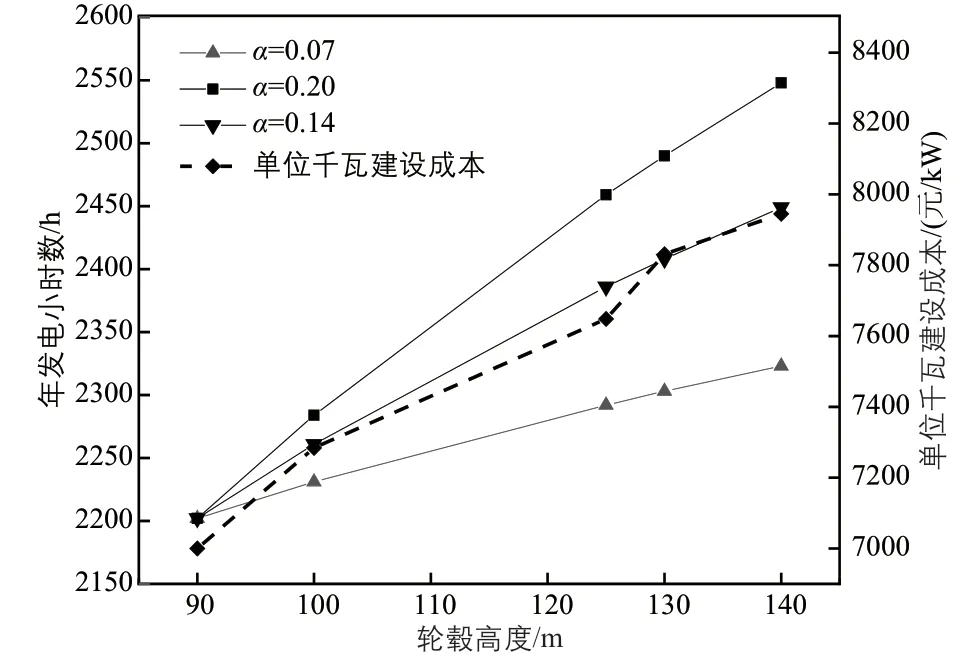
圖2 不同風切變指數下年發電小時數和單位千瓦建設成本隨輪轂高度的變化規律Fig. 2 Variation rule of annual power generation hours and construction cost per kilowatt with hub height under different wind shear indexes

由圖2可知：年發電小時數和單位千瓦建設成本隨著輪轂高度的升高而增加，但增加的速率呈現下降趨勢。風切變指數的大小與年發電小時數增加的速率基本呈正相關，風切變指數越大，年發電小時數隨輪轂高度升高而增加的速率就越快。

與此同時，結合風電機組輪轂高度選取模型，以財務凈現值作為評價指標，可選取不同風切變指數條件下的最佳輪轂高度，以實現風電場收益最大化。不同風切變指數下財務凈現值隨輪轂高度的變化關系如表5和圖3所示。

由表5和圖3可知：風切變指數為0.07時，90 m輪轂高度下的財務凈現值最大；風切變指數為0.14時，125 m輪轂高度下的財務凈現值最大；風切變指數為0.20時，140 m輪轂高度下的財務凈現值最大。

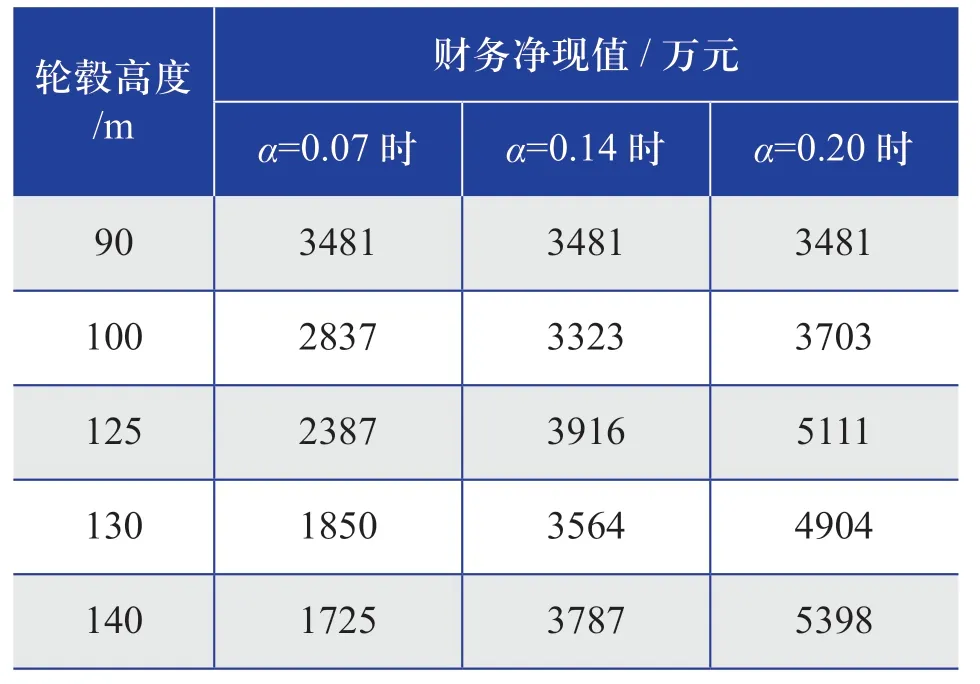
表5 不同風切變指數下財務凈現值隨 輪轂高度的變化關系Table 5 Relationship between financial net present value and hub height under different wind shear indexes

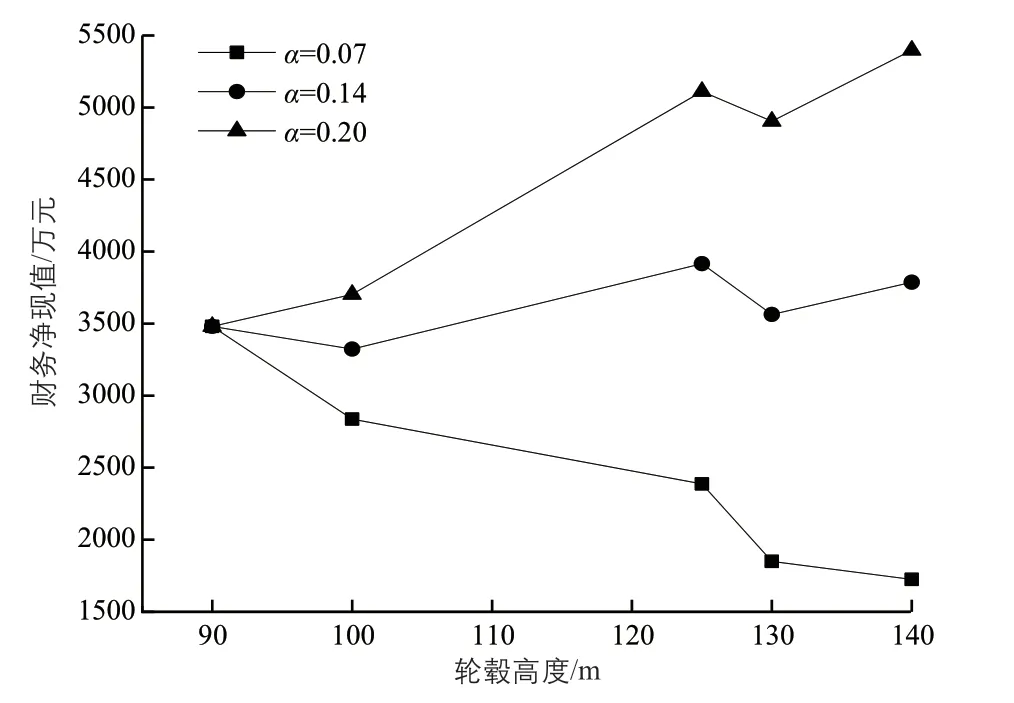
圖3 不同風切變指數下財務凈現值 隨輪轂高度的變化規律Fig. 3 Variation rule of financial net present value with hub height under different wind shear indexes

不同風切變指數下的最佳輪轂高度如表6和圖4所示。

由表6和圖4可知：隨著風切變指數增大，最佳輪轂高度也在增加。風切變指數在0.07～0.12之間時，最佳輪轂高度為90 m；風切變指數在0.13～0.16之間時，最佳輪轂高度為125 m；風切變指數大于等于0.17時，最佳輪轂高度為140 m。

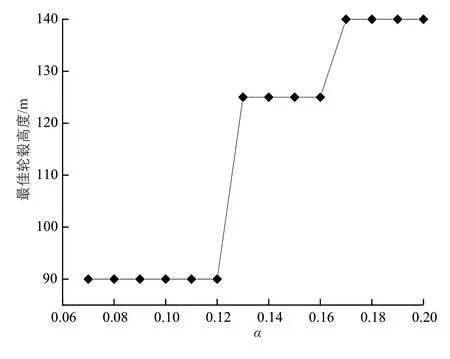
圖4 不同風切變指數下的最佳輪轂高度曲線Fig. 4 Curve of optimal hub heights under different wind shear indexes

表6 不同風切變指數下的最佳輪轂高度Table 6 Optimal hub height under different wind shear indexes

4 結論

風電場中的風電機組輪轂高度與風切變指數基本呈正比關系，風切變指數越大，輪轂高度越高，發電量越大，相應的投資成本也顯著增加。本文探討了風切變指數與風電機組輪轂高度之間的內在關系，構建了一種新的風電機組輪轂高度選取模型，綜合考慮輪轂高度提升帶來的發電收益增加和投資成本增加之間的關系，以財務凈現值作為不同風切變指數下風電機組輪轂高度選取的經濟指標，探討了不同風切變指數下最佳輪轂高度的選取結果，實現了風電場資源利用及收益的最大化。研究結果對風電場中風電機組輪轂高度的選取具有一定的參考意義。