考慮多性能參數的引信彈簧可靠性評估*

楊承強，顧曉輝，潘守華

(1. 南京理工大學 機械工程學院， 江蘇 南京 210094； 2.北方特種能源集團西安慶華公司， 陜西 西安 710025)

引信是彈藥實現有效毀傷目標的關鍵組件，其可靠性失效不僅會耽誤戰機甚至可能造成人員傷亡。彈簧作為一種常用的儲能元件，在引信中主要起到限制隔爆件運動或為擊針運動提供能量的作用，是影響引信可靠性的重要零件。根據在引信中作用效果的不同，彈簧主要有三種失效模式：疲勞斷裂、應力過強和應力松弛[1]。

國內外眾多學者對彈簧的可靠性進行了許多研究[2-3]。Manouchehrynia等[2]以汽車螺旋彈簧在隨機載荷下的疲勞可靠性預測為基礎，提出了一種估計應變壽命的概率模型，能有效預測彈簧的疲勞壽命；Ceyhanli等[4]對重型汽車的拋物線板簧靜強度和疲勞壽命可靠性進行了試驗和數值分析，得出該板簧在車輛試用期間可以安全使用的結論；付濤等[5]對高服役應力彈簧進行了疲勞試驗，并提出了一種基于支持向量機的彈簧疲勞壽命威布爾可靠性分析方法；王建平等[6]在不同溫度和初始載荷下對斜圈彈簧進行了加速退化試驗，并將Arrhenius方程理論與應力松弛理論相結合，研究彈簧參數與其壽命的關系。目前彈簧的可靠性評估大多針對工作狀態下的彈簧，而引信彈簧大部分時間處于貯存狀態。雖然有涉及彈簧貯存壽命的研究，但缺少對其貯存期間可靠度變化的預估。當前彈簧可靠性的研究往往只考慮應力損失率，缺乏對彈簧其他性能參數的考慮。彈簧作為高可靠性、長壽命產品，若只考慮單一性能參數，在進行試驗時，獲得的退化數據往往過少，導致可靠度評估結果不準確。

針對上述問題，本文提出一種基于修正Arrhenius模型的彈簧多元可靠性評估方法，以恒定應力加速退化試驗為手段，考慮彈簧多個性能參數，并根據修正的Arrhenius方程獲得貯存溫度下的退化軌跡曲線，同時采用Anderson-Darling統計量檢驗退化量的分布，建立基于多元正態分布的可靠度模型，通過與其他可靠度模型的對比，驗證了該方法的準確性。

1 試驗方案設計

1.1 試驗對象

試驗對象為引信圓柱螺旋彈簧，其長度為17.5 mm，線徑為0.40 mm，外徑為4.05 mm，節距為1.9 mm，采用軸向安裝方式，安裝后的裝配長度為5.8 mm。

1.2 試驗應力與樣本量的選擇

實踐經驗[7-8]表明，該彈簧在隨引信貯存時，熱應力是影響其性能退化最主要的因素，因此本試驗選擇溫度作為試驗加速應力。加速應力的選擇應遵循最高試驗溫度下與貯存溫度下失效機理保持一致的原則[9]。該材料的彈簧工作溫度范圍理論上為-100～200 ℃，因此最高試驗溫度確定為160 ℃。基于統計分析和試驗成本的考慮，設置4個試驗應力水平數，分別為T1=120 ℃、T2=130 ℃、T3=150 ℃、T4=160 ℃。

從理論上講，樣本量越大，最后估計的結果也越準確。但樣本量太大，會導致試驗成本(時間成本和人力成本)大大增加。經綜合考慮，在每個試驗溫度下投入8個樣本，共n=32個樣本。

1.3 性能退化參數與失效閾值的確定

1.3.1 應力損失率

彈簧常用的性能退化參數是應力損失率[10]，其定義為：

(1)

式中：δ為應力損失率，Pt為試驗后的彈簧彈力，單位為N；P0為彈簧初始彈力，單位為N。

供應方所給彈簧的規格要求規定了彈簧安裝后的彈力范圍，經計算應力損失率后考慮到安全性，向下取整得到失效閾值為7%。

1.3.2 永久變形率

彈簧應力松弛過程從宏觀角度出發實際上是一個由彈性應變向塑性應變轉換的過程[11]。在應力松弛過程中，彈性應變εe和塑性應變εp的和為一個常數c，即：

εe+εp=c

(2)

因此，選擇永久變形率作為另一個退化性能參數，其定義為：

(3)

式中：ε為永久變形率；Lt為試驗后彈簧的長度，單位為mm；L0為彈簧初始長度，單位為mm。

根據摸底試驗，將ε=5%作為永久變形率的失效閾值。

1.4 試驗檢測時間

有試驗表明[12]，彈簧前期退化快，后期退化慢。因此，為更好擬合彈簧的退化軌跡曲線，前期檢測頻率高，然后檢測頻率慢慢降低。具體的檢測時間見表1。

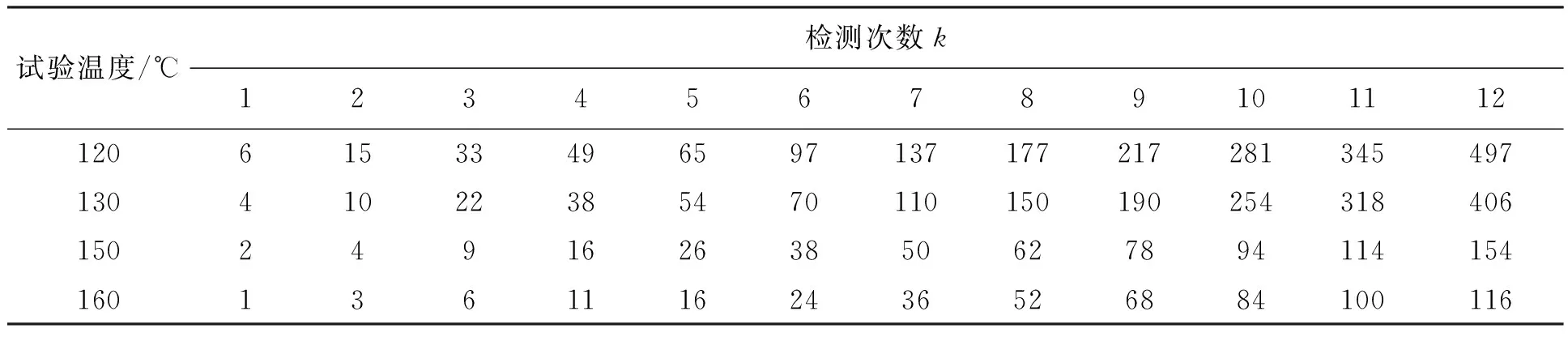
表1 性能參數檢測時間Tab.1 Degradation parameters detection time h

1.5 試驗設備

恒溫干燥箱(XMTD-9000，DHG型恒溫數顯干燥箱)1臺、數顯式壓力儀(精度為0.1 N)1臺、視頻顯微鏡1臺、臺式計算機1臺和游標卡尺1把。

試驗設計了專用安裝夾具，共32個。夾具材料為LC4硬鋁材料，其由套筒、蓋板、螺栓、螺母和防松墊圈組成，如圖1所示。套筒內徑略大于彈簧外徑，蓋板下側有一圓形凹槽，直徑與彈簧外徑相等，起固定彈簧的作用。該安裝方式能最大程度上模擬彈簧在引信中真實的安裝狀態。套筒的槽深為夾具關鍵尺寸，該尺寸采用精加工以減小夾具不同而產生的差異。

圖1 夾具與安裝Fig.1 Fixture and installation

1.6 數據測量

從同一生產批次的圓柱螺旋彈簧中，隨機抽取32個，平均分為4組分別放入120 ℃、130 ℃、150 ℃、160 ℃的恒溫干燥箱中，按表1中的時間取出，并在室溫下冷卻3 h后進行測量[13]。

彈簧應力用數顯式壓力儀進行測量。先尋找彈簧壓縮的起始點，然后將彈簧置于測量夾具中，使測量探頭壓縮彈簧到規定值，然后讀取穩定顯示的壓力讀數。

彈簧長度采用計算機視覺的方法測量。將彈簧置于游標卡尺上，然后用視頻顯微鏡進行拍照。在臺式計算機上打開長度測量程序，先進行長度標定(標定距離為15 mm)，然后選取彈簧兩端即可得到其長度，最后通過重復測量取均值來減小人為誤差。該測量方法的精度達0.001 mm。

1.7 數據處理

按式(1)和式(3)計算每個樣品在各檢測點的應力損失率δ和永久變形率ε，其退化曲線如圖2所示。

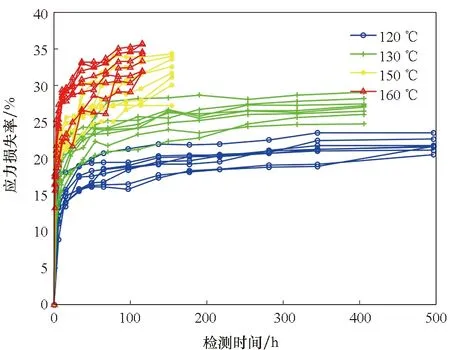
(a) 應力損失率(a) Stress loss rate

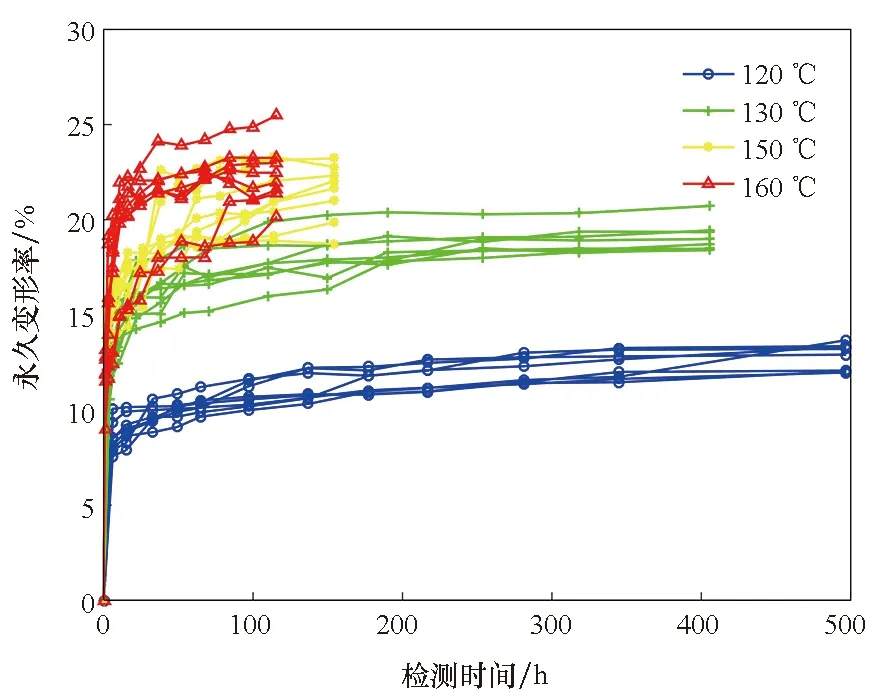
(b) 永久變形率(b) Permanent deformation rate圖2 性能參數退化曲線Fig.2 Performance parameter degradation curve

檢驗加速應力下貯存失效機理的一致性，相當于檢驗退化軌跡曲線的形狀是否近似[14]。從圖2可以看出兩個性能參數在各加速應力下的退化軌跡曲線是相似的，并且通過計算Spearman秩相關系數可驗證該結論。

2 基于修正Arrhenius模型的回歸分析

2.1 性能退化軌跡方程

經分析可知[15]，彈簧的兩個性能退化過程可表達為：

yz=azln(t)+bz

(4)

式中：yz為彈簧第z(z=1,2)個退化過程的退化量；az為第z個退化過程的退化速率；bz為第z個退化過程的模型常數；t為退化時間，單位為h。

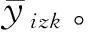
(5)

式中：yijzk為第i(i=1,2,3,4)個應力水平下第j(j=1,2,…,8)個樣本第z(z=1,2)個退化過程第k次檢測的退化數據。

表2 退化軌跡模型的參數估計值Tab.2 Parameters estimate of degradation curve model

設顯著水平為0.01，查相關系數臨界表得r0.01=0.834 0。表2中的相關系數均大于0.834 0，因此4組退化軌跡方程的線性回歸效果顯著。

2.2 修正Arrhenius模型

由于加速應力為熱應力，所以加速模型首選Arrhenius模型，即：

(6)

式中：a為退化速率；A為Arrhenius常數；Ea為活化能；T為絕對溫度；R為玻爾茲曼常數。

數據分析時，發現反應速率a與1/T并不是一條很好的直線。經研究后得知[16]，這是由于Arrhenius模型的前提假設認為活化能Ea是與溫度無關的常數，這在一定溫度范圍內是正確的。然而大量實踐表明[17-18]，對于溫度范圍較大或較復雜的反應過程，活化能Ea與溫度T有關。 因此，采用修正的三參數Arrhenius模型作為加速模型[19]：

(7)

式中：E0為試驗活化能，與溫度無關；m是[-2,2]之間的整數或半整數。

對式(7)兩邊取對數，并令Y=lna，c=ln (A)，d=-E0/R，可得：

Y=c+mlnT+d/T

(8)

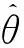
(9)

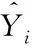
經計算得到性能參數退化速率的加速方程。此時，退化速率的殘差平方和分別為I1=0.015 2、I2=0.017 6。

a1=exp(-7.118+2lnT-1 631/T)

(10)

a2=exp(-6.857+2lnT-1 969/T)

(11)

式中：a1和a2分別是應力損失率和永久變化量的退化速率。

式(4)中的b可以看作1 h后的退化量，根據修正的Arrhenius方程可得：

(12)

采用上述同樣方法，可得：

b1=exp(22.33-2lnT-2 971/T)

(13)

b2=exp(23.54-2lnT-3 618/T)

(14)

此時，殘差平方和分別為I3=0.010 7，I4=0.051 0。

貯存彈藥的庫房一般會嚴格控制溫度，因此設彈簧隨引信貯存的環境溫度為T0=25 ℃，按式(10)、式(11)、式(13)、式(14)可計算出彈簧在貯存溫度T0下性能參數的退化軌跡方程，并得到在25 ℃下彈簧的性能退化曲線，如圖3所示。

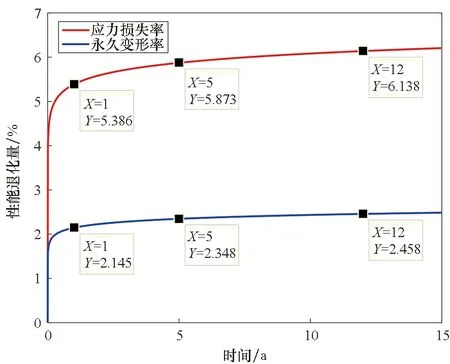
圖3 在25 ℃下彈簧的退化軌跡曲線Fig.3 Degradation trajectory curve at 25 ℃

μ1=0.302 5ln(t)+2.640

(15)

μ2=0.126 0ln(t)+1.001

(16)

式中：μ1和μ2分別表示應力損失率的退化均值和永久變形率的退化均值；t為彈簧貯存時間，單位為h。

3 多性能參數的可靠性評估

根據修正的Arrhenius方程外推獲得彈簧在溫度T0=25 ℃下的退化軌跡方程，由此就可預估彈簧在貯存期間的可靠度變化。

3.1 退化量分布的檢驗

正態分布和威布爾分布是可靠性評估中最常用的分布類型。采用Anderson-Darling(AD)檢驗[20]，對不同試驗溫度Ti下樣品性能參數的退化量分布進行擬合優度檢驗。應力損失率δ和永久變形率ε的AD統計量和p值的計算結果分別見表3和表4。

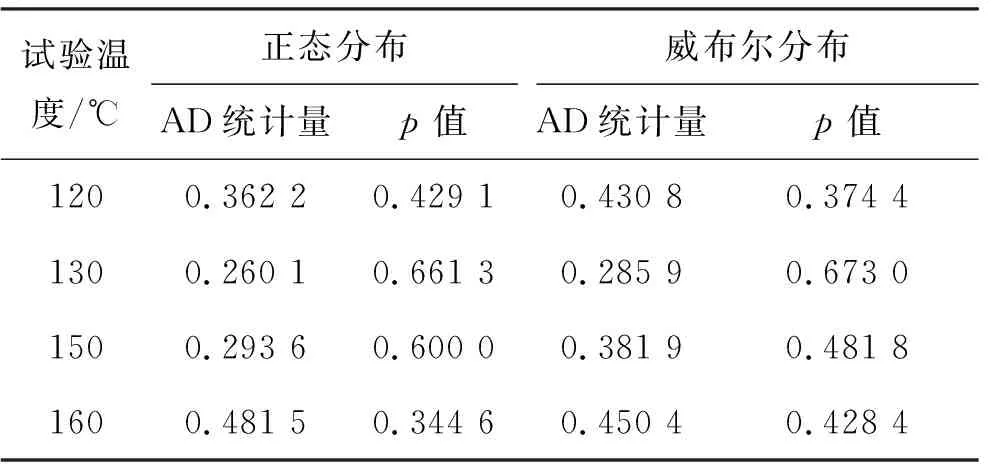
表3 應力損失率的AD檢驗Tab.3 AD test of stress relaxation rate

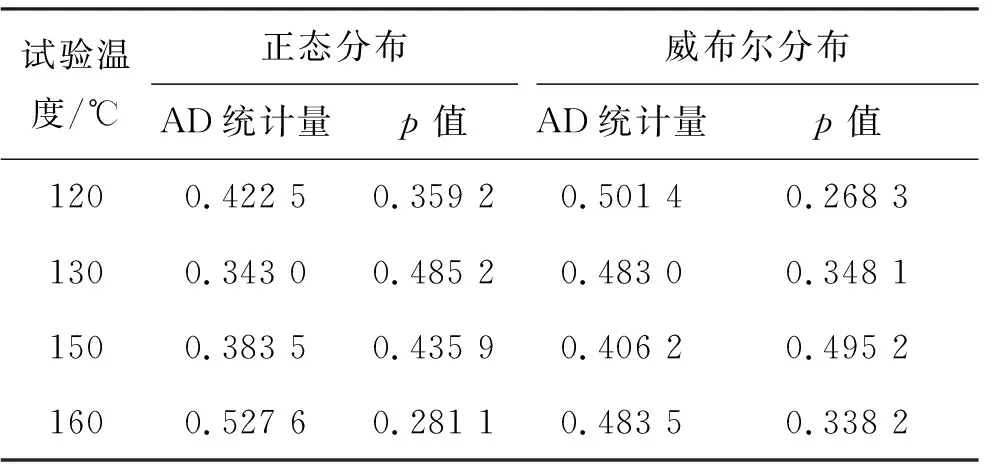
表4 永久變形率的AD檢驗Tab.4 AD test of permanent deformation rate

表3和表4中的p值均大于顯著水平0.05，并且應力損失率和永久變形率的正態分布AD統計量均值為0.349 4和0.387 3，分別小于其威布爾分布的AD統計量均值0.419 2和0.468 5，所以樣品應力松弛和永久變形退化數據的最優分布均為正態分布，即：

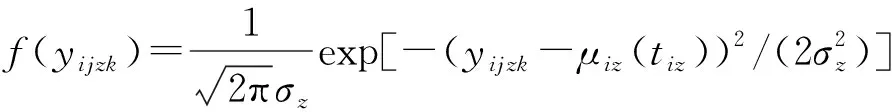
(17)

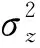
3.2 基于二元正態分布的可靠度模型

記Y=(δ,ε)T表示彈簧性能參數向量，根據退化量分布檢驗的結果，可得應力損失率和永久變形率兩個性能參數的向量服從二元正態分布，即：

(18)

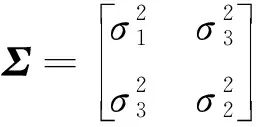
Cov(yZ,yz)=E[(yZ-E(yZ))(yz-E(yz))]

(19)

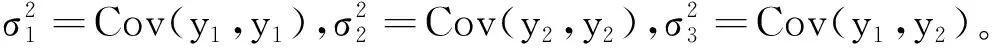
按式(19)計算性能參數退化數據的協方差為：

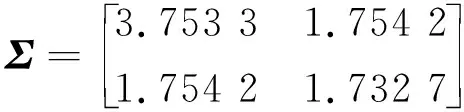
(20)

在給定性能參數失效閾值的情況下，對式(18)積分可以得到彈簧在t時刻的可靠度模型，即：

Rr(t)=P[δ≤7,ε≤5]

(21)

由此，根據式(21)給出在15 a內彈簧的可靠度隨貯存時間的變化，如圖4所示。

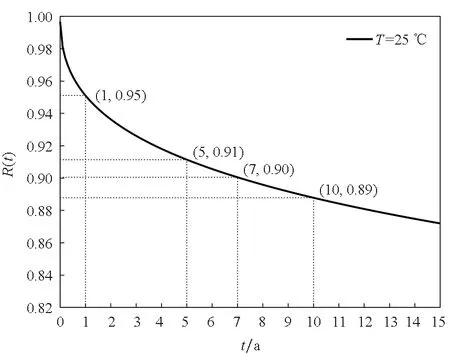
圖4 雙參數相關的可靠度曲線Fig.4 Two-parameter reliability curve

從圖4可知，該彈簧貯存1 a后，其可靠度從1降到0.95左右，之后進入緩慢退化階段。當可靠度為0.90時，該彈簧的貯存壽命為7 a，基本滿足引信貯存需要。在貯存7 a后，維護人員需密切關注引信中彈簧的性能退化情況，及時采取相應的處理措施。

可靠度分析情況如圖5所示。從圖5中可以看出，彈簧在T0=25 ℃下貯存時，其可靠度曲線不同于一般的可靠度曲線(S形曲線，分為平穩期—速降期—平穩期)，而是L形曲線(速降期—平穩期)。①彈簧的性能失效閾值較低，通常都在10%以下，遠低于其他產品的失效閾值(如橡膠圈的失效閾值在30%左右)，這導致退化量分布離閾值近，所以彈簧一開始就是速降期；②在貯存初期，彈簧退化速率快，但持續時間短，所以其可靠度曲線的速降期時間也很短；③該引信彈簧個體差異較大(退化量方差較大)，而且退化到一定程度后開始非常緩慢地退化，所以其可靠度曲線的平穩期非常長，并且可靠度幾乎永遠不會到0。

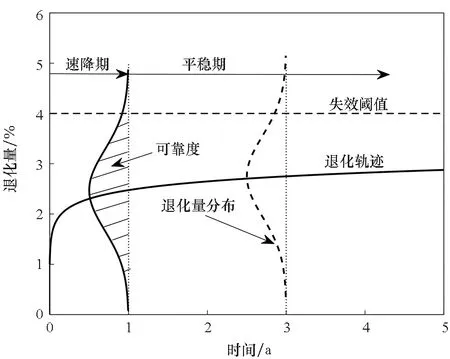
(a) 彈簧的可靠度分析(a) Spring reliability analysis

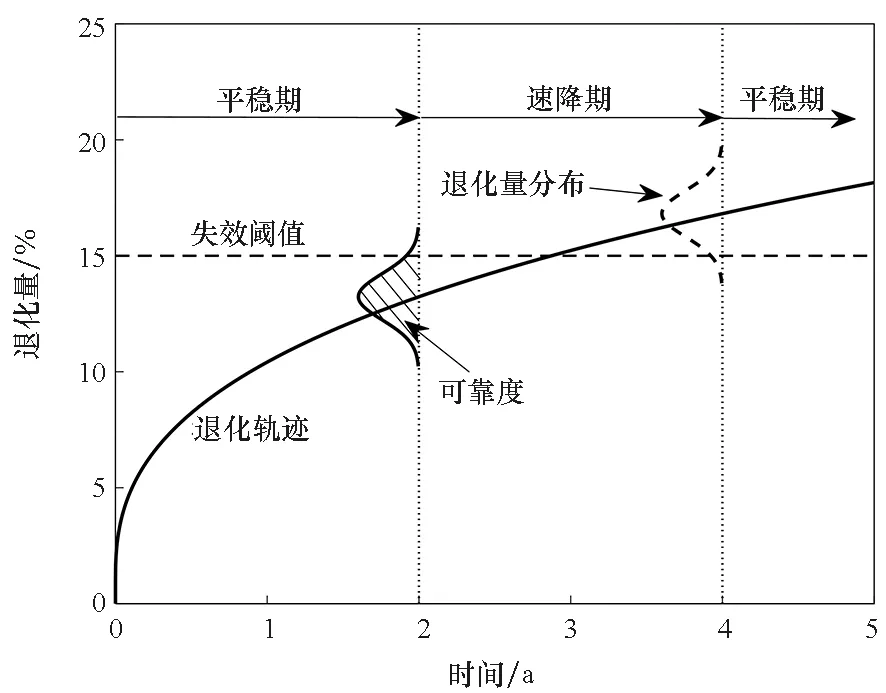
(b) 其他產品的可靠度分析(b) Other product reliability analysis圖5 可靠度分析Fig.5 Reliability analysis

4 評估結果分析

若只將應力損失率作為性能參數，根據式(15)、式(17)、式(20)可以得到應力損失率δ的可靠度模型：

(22)

式中：Φ(·)表示標準正態分布的累積概率函數。

由此，根據式(22)可以得到彈簧應力損失率的可靠度曲線，如圖6(a)所示。

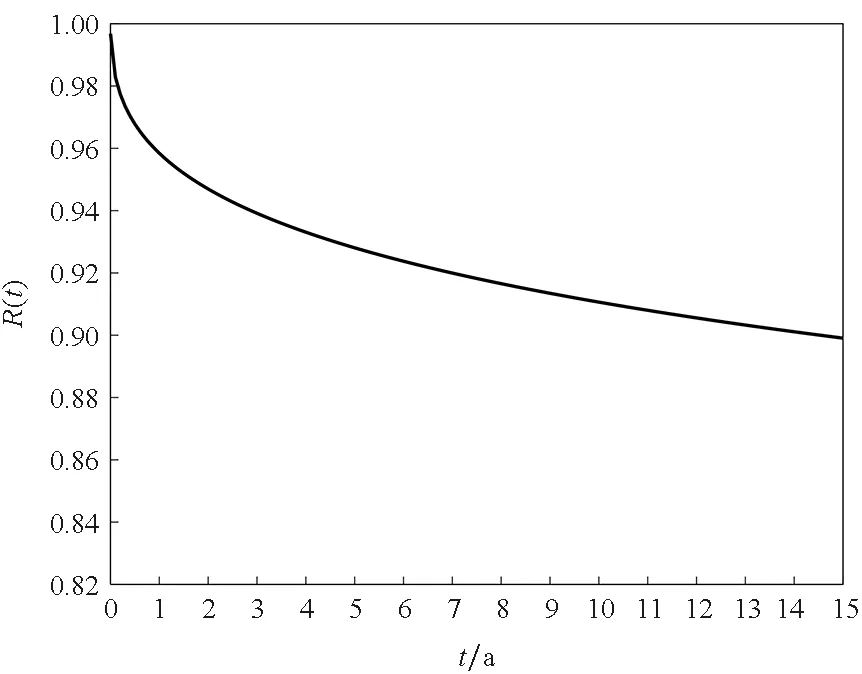
(a) 應力損失率(a) Stress loss rate

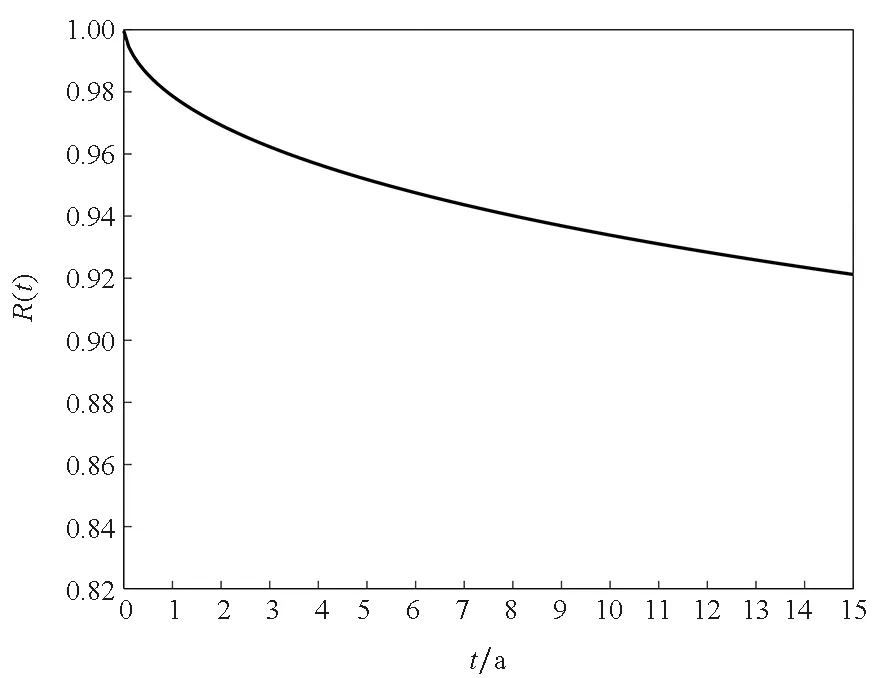
(b) 永久變形率(b) Permanent deformation rate

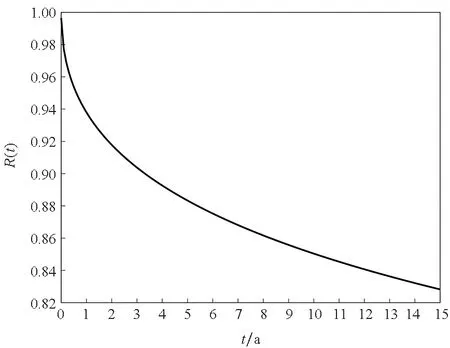
(c) 兩者獨立(c) Both independent圖6 可靠度曲線Fig.6 Reliability curve

若只將永久變形率作為性能參數，根據式(16)、式(17)、式(20)可以得到永久變形率ε的可靠度模型：

(23)

由此，根據式(23)可以得到彈簧永久變形率的可靠度曲線，如圖6(b)所示。

當應力損失率和永久變形率互相獨立時，根據式(22)、式(23)可以得到在兩者獨立情況下的彈簧可靠度模型：

Rv(t)=Rs(t)·Rt(t)

(24)

根據式(24)可以得到彈簧兩個性能參數獨立時的可靠度曲線，如圖6(c)所示。

通過上述討論，可以比較彈簧應力損失率的可靠度Rs(t)、永久變形率的可靠度Rt(t)、兩者獨立時的可靠度Rv和兩者相關時的可靠度Rr，曲線對比如圖7所示。

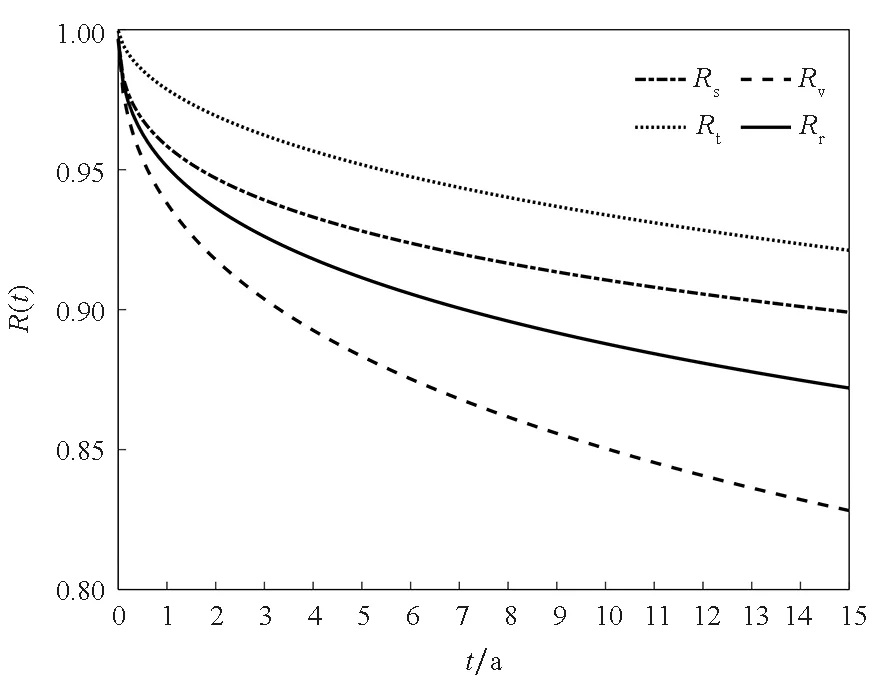
圖7 可靠度曲線對比Fig.7 Reliability curve contrast

從圖7可以看出，不論哪個可靠度曲線，其共同特點是：前期可靠度快速下降，后期緩慢下降。因此，為了更好保證引信可靠性，建議對采購的彈簧進行環境試驗篩選，避免給引信裝配性能退化過快的彈簧，從而降低引信故障率。

對比雙參數相關的可靠度Rr與單參數的可靠度Rs和Rt可以看出，用單參數的可靠度會高估彈簧貯存期間的可靠性，所估計的彈簧貯存壽命偏長，這將導致維修不及時，可能造成安全隱患。

對比雙參數相關的可靠度Rr與雙參數不相關的可靠度Rv可以發現，兩個參數獨立會明顯低估彈簧貯存期間的可靠性，導致引信提早更換，造成資源浪費，降低經濟效益。考慮相關性后的可靠度Rr更加接近工程實際。

綜上可得，本文的可靠度模型相比其他模型可以較準確地預估彈簧貯存期間的可靠度變化，不僅能提高引信的安全性，而且考慮了其經濟性。

5 結論

1) 通過恒定應力加速退化試驗，獲得彈簧應力損失率和永久變形率的退化數據，并對數據展開統計分析，利用修正的Arrhenius方程進行外推計算，得到彈簧在貯存溫度T0=25 ℃時的退化軌跡。

2)采用Anderson-Darling統計量驗證樣品退化量最優分布為正態分布，并基于二元正態分布得到彈簧雙參數相關的可靠度模型。

3) 通過與其他可靠度模型對比，表明本文建立的可靠度模型能更好地反映彈簧實際的可靠度變化，對研究彈簧在貯存條件下的可靠度具有一定的參考價值與指導意義。