扭擺式多方向壓電振動俘能器的研究

闞君武 吳亞奇 張忠華 何恒錢 孟凡許

1.浙江師范大學精密機械與智能結構研究所，金華，321004 2.浙江省城市軌道交通智能運維技術與裝備重點實驗室，金華，3210043.浙江清華柔性電子技術研究院，嘉興，314006

0 引言

為實現傳感器的能量自給、避免廢棄電池污染環境，基于電磁、摩擦、壓電等原理的微小型俘能器的研究成為國內外的前沿熱點[1-5]。每一類微型俘能器都有其自身的優勢和適用領域[6]，壓電俘能器的優勢在于結構簡單、無電池干擾、易于實現結構上的微小化，故其適用范圍更廣，已逐步用于俘獲自然環境中振動能[7]、人體動能[8]、旋轉機械動能[9]及流體動能[10]等能量。這些能量最終都是通過壓電振子的振動轉化為電能[11]。

傳統的壓電振動俘能器大都采用端部固定有質量塊的壓電振子作為換能部件，所適應的振動方向單一、有效頻帶窄，無法滿足多向振動、頻率變化范圍較大場合的傳感器自供電需求[12]，故國內外學者將研究重心轉向多方向振動俘能器。WANG等[13]將PVDF壓電薄膜粘貼于懸臂圓柱的根部用以發電，以便有效捕獲多方向的振動能量，但該俘能器僅在一個共振峰下工作，有效頻帶窄。ZHAO等[14]設計了一種空間螺旋結構的俘能器，可沿空間多個方向伸縮、彎扭變形，對空間各方向均有較好的輸出響應，然而，其壓電振子工作時產生雙向彎曲變形，壓電片承受交變的拉-壓應力，易因變形過大而損毀。CHEN等[15]在空間多個方向上布置了懸臂梁壓電振子，某一方向的振動都能使部分壓電振子產生響應，但壓電振子密度過大時會相互干涉。YUAN等[16]提出了一種基于并聯機構的六自由度俘能器，可實現多向振動能量的收集，但結構過于復雜。ALGHISI等[17]提出一種撞擊式多方向振動俘能器，利用自由運動的鋼球撞擊各側面上設有壓電振子的框架結構發電，但工作的撞擊不僅會產生噪聲，也易導致壓電晶片脫落。

在總結分析國內外研究現狀的基礎上，為實現多方向振動能量的有效回收，提高俘能器的多方向振動響應能力及可靠性，本文提出一種扭擺式多方向壓電振動俘能器，并從有限元仿真與試驗兩方面進行了研究。

1 俘能器的結構及原理

扭擺式多方向壓電振動俘能器的結構原理如圖1所示，主要由壓電振子、彈性梁、錘頭、擺桿和壓塊組成。錘頭、擺桿和彈性梁構成激勵器。壓電振子由金屬基板與壓電晶片粘接而成，壓電振子的自由端經壓塊頂靠在彈性梁上。

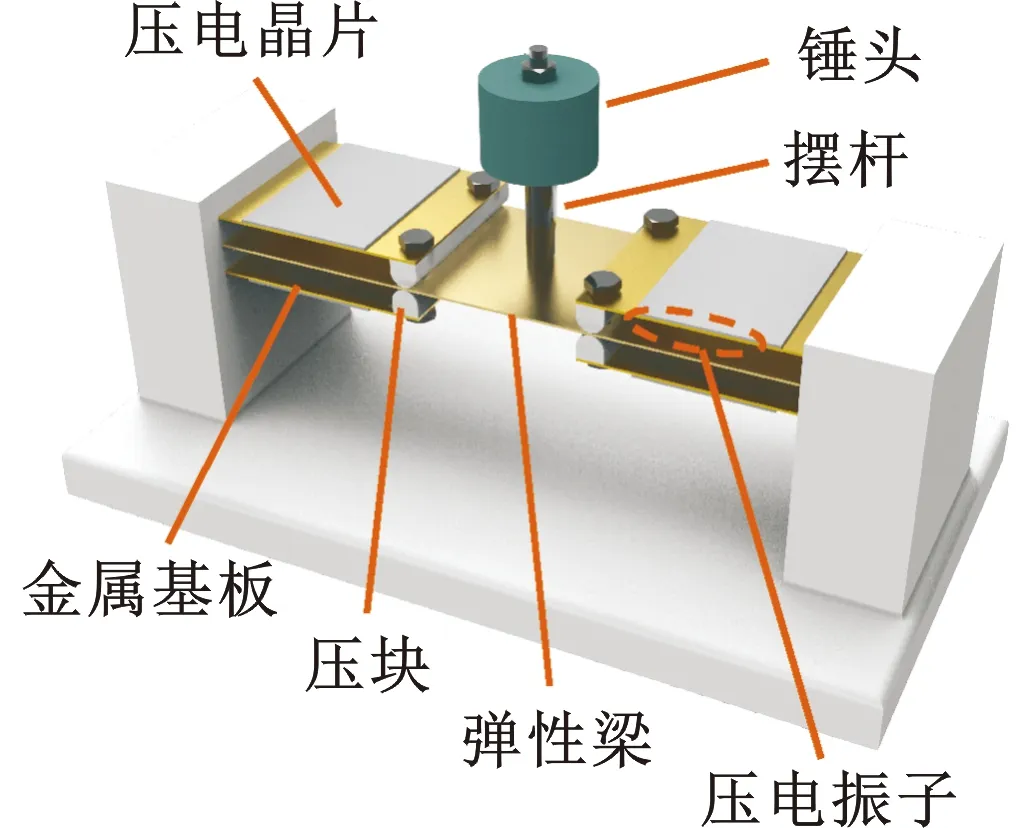
(a)結構原理

(b)一階諧振 (c)二階諧振圖1 俘能器結構示意圖Fig.1 Structures diagram of energy harvester

當俘能器受到某一方向的激振力時，激勵器在慣性力的作用下產生扭擺變形，通過彈性梁迫使壓電振子產生單向彎曲變形而發電。因壓電振子的彎曲變形是由彈性梁間接接觸導致的，當彈性梁發生多階變形時壓電振子都以上下彎曲變形為主，使壓電晶片僅沿壓應力單向變形，故所受拉應力較小。

2 有限元仿真分析

目前，難以建立一個精確的解析模型來進行俘能器振動模態及動態響應特性分析，故本文通過有限元建模仿真方法進行研究，所建立的COMSOL有限元模型如圖2所示，其坐標系原點為彈性梁的幾何中心。根據有限元仿真的需要，將彈性梁夾持區域端點作為后續繪制動力學響應曲線的位移參考點，通過該點在Z軸方向上的位移來表征俘能器的輸出電壓。仿真中涉及的相關結構參數如表1所示。

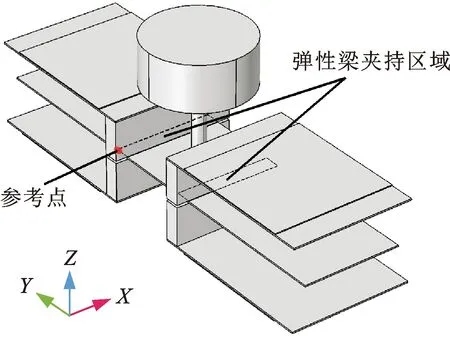
圖2 有限元幾何模型Fig.2 Finite element geometric model

圖3給出了俘能器的模態振型，其中圖3a、圖3b分別為激勵器繞Y軸和X軸扭轉的模態振型，所對應的固有頻率分別稱為第一、二階固有頻率，其仿真結果分別為fn，1=35.4 Hz和fn，2=52.9 Hz。俘能器受到某一方向的激振力時，激勵器激勵壓電振子使其發生彎曲變形。因壓電振子端部頂靠在彈性梁上，故激勵器發生第一階和第二階諧振時，壓電振子仍以彎曲變形為主。

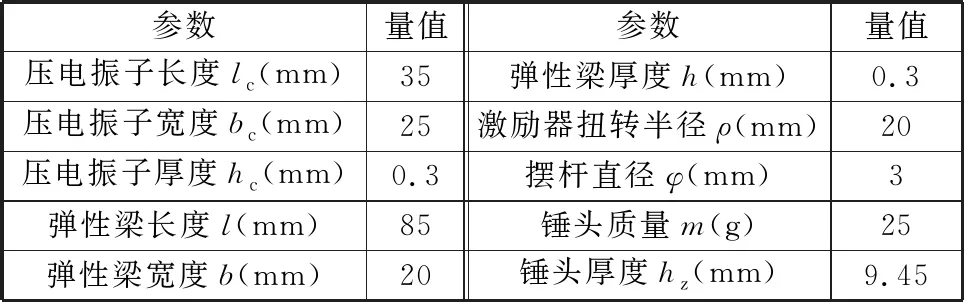
表1 仿真涉及的相關結構參數

(a)一階振型 (b)二階振型圖3 俘能器的模態振型Fig.3 Modal shapes of the energy harvester

為便于敘述，將激勵器振動方向(激勵方向)與X軸在XOY平面內的夾角θ稱為激勵角。圖4為不同激勵角時俘能器的動力學響應曲線。圖中曲線的變化趨勢表明：激勵角變化對兩階諧振頻率影響均較小，但對輸出電壓的影響較大且影響規律不同。激勵角從0°增加到90°時，第一階諧振電壓減小，激勵角θ=90°時因電壓較小而未顯現，第二階諧振電壓增大，激勵角θ=0°時因幅值較小而未顯現。

圖4 激勵角不同時俘能器的動力學響應特性曲線Fig.4 Dynamic responses of the energy harvester when the angle of excitation changes

圖5為不同激勵角θ時第一階和第二階諧振峰幅值(D1和D2)的變化曲線。圖中曲線在360°的角度范圍內關于0°-180°直線及90°-270°直線對稱，即每90°對稱循環一次。在整個角度變化域內，俘能器的最大響應位移構成圖中曲線的包絡線。顯然，在XOY平面內俘能器響應無死角，即該俘能器理論上能對水平面內任意方向的振動能量做出有效響應。

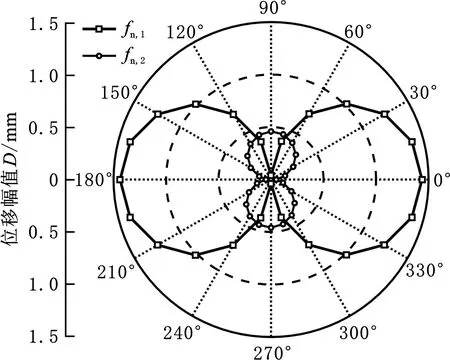
圖5 激勵角不同時諧振峰幅值的變化曲線Fig.5 The change curves of resonance peak of the energy harvester when the angle of excitation changes

3 試驗測試與分析

為探究壓電振動俘能器的輸出特性并驗證仿真結果的正確性，設計制作了圖6所示的試驗測試平臺。試驗儀器主要包括ECON VT-9008/8振動控制器、Premax VSA-L800A功率放大器、Premax LT-50ST振動臺、Rigol MSO6014A 型混合信號示波器、變阻箱等。試驗樣機主要由壓電振子、彈性梁、錘頭和擺桿組成，見圖7。壓電振子尺寸為35 mm×25 mm×0.3 mm，壓電晶片為φ35 mm×0.2 mm，激勵器中彈性梁尺寸為85 mm×20 mm×0.3 mm，擺桿為φ3 mm×50 mm，扭擺半徑為20 mm，附加25 g錘頭。試驗結構參數與仿真所用的結構參數一致。試驗中，通過調整樣機的安裝方位來改變激勵角。

圖6 測試平臺Fig.6 Testing platform

圖7 試驗樣機Fig.7 Test prototype

根據仿真結果，激勵角不與X、Y軸重合時俘能器會出現兩個諧振峰。以θ=45°為例，得到圖8所示的兩個諧振頻率處的電壓波形。由圖8可知，俘能器發生第一階諧振(40 Hz)時，在140 ms的時間跨度內俘能器的電壓波形數量為10或11，而振動信號的理論波形數量是5.6，二者約為2倍關系。這是因第一階諧振時，激勵器沿著X軸左右扭擺，一個周期內彈性梁對單片壓電振子進行兩次激勵。俘能器發生第二階諧振(53 Hz)時，激勵器沿著Y軸前后扭擺，此時一個振動周期內激勵器對壓電振子僅產生一次激勵，因此波形數量與激勵頻率一致，理論波形數量為7.42，實際波形數量為7或8，圖中明顯較小的波形為振蕩所致。

圖8 電壓波形圖Fig.8 Voltage waveform

根據仿真結果，當激勵角變化時，兩階諧振峰變化曲線每隔90°對稱循環一次，故試驗中著重研究θ=0°～90°的幅頻特性。圖9給出了不同激勵角時輸出電壓的幅頻特性曲線。圖9與圖5的結果均表明：激勵角變化對兩階諧振頻率影響較小，但對其輸出電壓的影響較大且影響規律不同。圖9出現了仿真中并未出現的波動以及幅值大小的改變，該現象可能的原因為加工和安裝誤差以及壓電振子與彈性梁接觸等不可控因素的存在。根據試驗結果，俘能器的第一、二階諧振頻率分別為40 Hz和53 Hz，這與仿真結果基本一致。

圖9 激勵角不同時輸出電壓的幅頻特性曲線Fig.9 The change curves of output voltage versus frequencies of the energy harvester when the angle of excitation changes

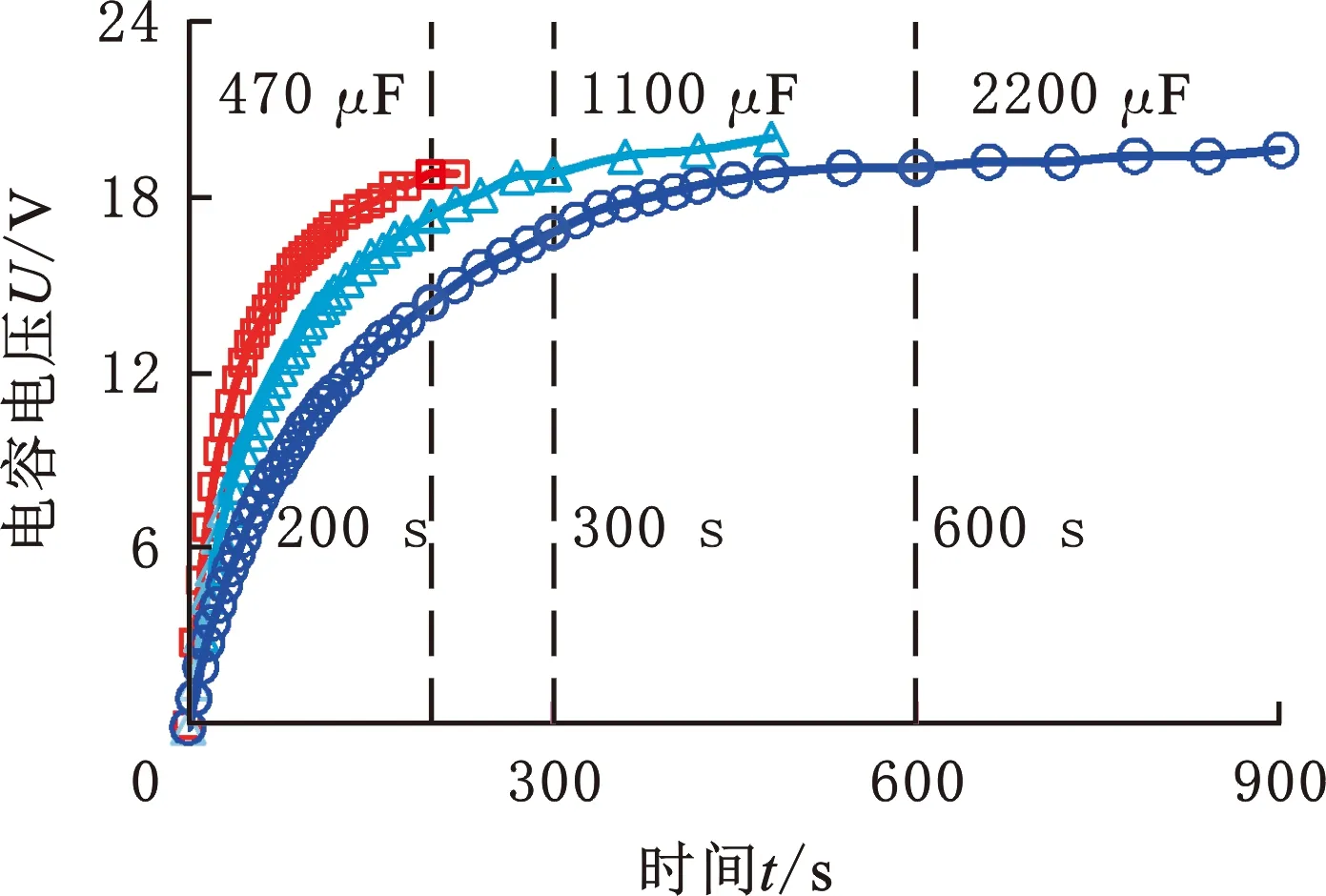
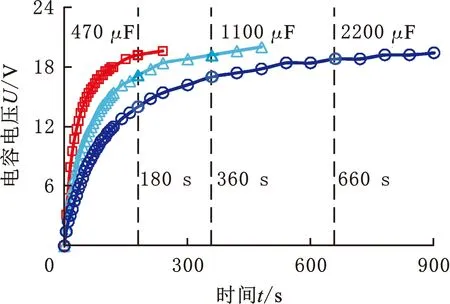
為方便敘述，將第一階和第二階諧振頻率(fn，1，fn，2)對應峰值電壓分別稱為第一階和第二階諧振電壓(Un，1，Un，2)。圖10給出了兩階諧振電壓與激勵角的關系曲線，圖11給出了兩階諧振頻率與激勵角的關系曲線。由圖中曲線的變化趨勢可以看出，激勵角對諧振頻率影響較小，對諧振電壓影響較大；隨激勵角θ增加，第一、二階諧振頻率幾乎不變，但其對應的諧振電壓不同，即第一階諧振電壓Un，1降低且降低速率逐漸增大，第二階諧振電壓Un，2升高且升高速率逐漸減緩；存在激勵角θ=44°使得兩階諧振電壓相等(Un，1=Un，2)，當θ<44°時Un，1>Un，2，當θ>44°且其他激勵條件不變時Un，1

圖10 激勵角對諧振電壓的影響Fig.10 The relation curve of excitation angle to resonance voltage

圖11 激勵角對諧振頻率的影響Fig.11 The relation curve of excitation angle to resonance frequencies

隨激勵角θ增加，Un，1降低、Un，2升高的原因在于：當θ=0°時，激振力F沿X軸方向，俘能器繞著Y軸扭擺相對較大，故第一階諧振峰幅值較大；同理，當θ=90°時，激振力F沿Y軸方向，第二階諧振峰幅值最大。θ=0°時出現微小第二階諧振峰及θ=90°時出現微小第一諧振峰的原因可能是制作及安裝誤差所致。

以上給出的是俘能器輸出電壓的特性，當俘能器所生成的電能不被實時利用時，需進行存儲。為獲得電容儲能特性，選取容量為470，1100，2200 μF的電容進行了充電試驗。圖12和圖13分別給出了(θ=0°、f=40 Hz)和(θ=90°、f=53 Hz)情況下充電特性曲線。由圖可知，在電容飽和時充電時間隨電容容量的增加而增長，但所達到的飽和電壓基本相同。①θ=0°、f=40 Hz時，容量為470，1100，2200 μF的飽和充電時間為200，300，600 s，所對應的電壓分別為18.8，18.8，19 V，即分別儲存能量0.083，0.194，0.397 J；②θ=90°、f=53 Hz時，容量為470，1100，2200 μF的飽和充電時間為180，360，660 s，所對應的電壓分別為19.2，19.2，18.8 V，即分別儲存0.087，0.203，0.389 J。根據試驗結果，沿X軸和Y軸方向激勵時，電容的存儲速度分別達到0.58 mJ/s和0.54 mJ/s。

圖12 沿X軸方向激勵時電容的充電特性曲線Fig.12 The charging curves of the energy harvester under X-axis excitation

圖13 沿Y軸方向激勵時電容的充電特性曲線Fig.13 The charging curves of the energy harvester under Y-axis excitation

除了輸出電壓、電能存儲外，輸出功率是評價俘能器發電能力的又一關鍵要素。圖14給出了沿X軸和Y軸激勵時各壓電振子的平均功率P與負載電阻R的關系曲線。由圖可知，沿X軸和Y軸激勵時，均存在兩個最佳負載使輸出功率最佳。沿X軸方向激勵時，兩個最佳負載電阻及其所對應的最佳功率分別為(17，81)kΩ和(4.56，3.4)mW；沿Y軸方向激勵時，兩個最佳負載電阻及其所對應的最佳功率分別為(17，61)kΩ和(3.96，3.89)mW。上述試驗中，單一激勵方向時出現兩個最佳負載的可能原因在于：各壓電振子自身動力學特性及阻抗特性存在一定的差異，彈性梁上下兩側壓電振子初始受力狀態有所不同。

圖14 輸出功率與負載電阻的關系曲線Fig.14 The change curves of output power versus load resistance

4 結論

為實現多方向振動能量回收，提出一種扭擺式多方向壓電振動俘能器，通過錘頭、擺桿和彈性梁構成的激勵器間接、單向激勵壓電振子，優勢在于：可收集水平面內任意方向的振動能量；彈性梁多階模態振動時壓電振子均發生單向彎曲變形，所受拉應力較小。從有限元仿真和試驗兩方面對其進行了研究，獲得了激勵方向不同時輸出電壓、電容充電及輸出功率特性，具體結論如下：

(1)俘能器可回收平面內任意方向的振動能量，但不同激勵方向發電特性不同。激勵角在0°～360°變化時，各階諧振峰每隔90°對稱循環一次；激勵角從0°增加到90°時，第一、二階諧振頻率均基本不變，但其所對應的諧振電壓變化不同，即第一階諧振電壓降低且降低速率逐漸增大，第二階諧振電壓升高且升高速率逐漸減緩。存在激勵角θ=44°使得兩階諧振電壓相等。

(2)電容飽和充電時間隨電容容量的增加而增長，但所達到的飽和電壓基本相同。沿X軸方向激勵時，容量為470，1100，2200 μF的電容飽和充電時間為200，300，600 s，所對應的電壓分別為18.8，18.8，19 V；沿Y軸方向激勵時，容量為470，1100，2200 μF的飽和充電時間為180，360，660 s，所對應的電壓分別為19.2，19.2，18.8 V。沿X軸和Y軸方向激勵時，電容的存儲速度分別達到0.58 mJ/s和0.54 mJ/s。

(3)沿X軸和Y軸激勵時，均存在兩個最佳負載電阻使輸出功率最佳。沿X軸方向激勵時，最佳負載電阻及其最佳功率分別為(17，81)kΩ和(4.56，3.4)mW；沿Y軸方向激勵時，最佳負載阻值及其最佳輸出功率分別為(17，61)kΩ和(3.96，3.89)mW。