指向深度學習的深度教學*
——以圓錐曲線定義法求最值問題為例

劉璇燕

廣東省廣州市番禺區實驗中學 (511400)

數學深度教學是幫助學生“通過數學會思維”，學會總結反思和“再認識”，強調通過“聯系的觀點”幫助學生更好地學會學習，深入學習，從而真正成為學習的主人的教學.單元復習教學中，圍繞教學中的重難點，通過對相關題目的背景分析、解法思考等追溯題目的根源，變式拓展探尋題目本質內涵，找尋學生解題能力生長的軌跡，是很好的復習策略.本文以圓錐曲線定義法求最值問題為例，談談自己對“深度教學”的感受和思考.

1 問題呈現

例1 拋物線y2=4x的焦點為F，定點Q(2，1)，P為拋物線上動點，則|PF|+|PQ|的最小值為.

分析：本題考查拋物線的定義、簡單幾何性質和數形結合思想，是一道基礎題.由點Q在拋物線內側，作圖(略)，把拋物線上的點到焦點的距離轉化為到準線的距離，但是在課前練習中只有一半的學生能夠求出正確答案3.分析作業情況主要原因有三個：缺乏數形結合意識，沒有判斷定點與拋物線的位置關系；不能靈活運用拋物線定義進行轉化；對于能夠運用拋物線定義轉化寫出正確答案的部分學生，問其思路原因時，都說是印象中就是這樣解題的，但卻不清楚為什么要進行轉化.針對這種情況，筆者進行了以下的變式練習探尋題目本質內涵.

變式1 拋物線y2=4x的焦點F，定點Q(3，4)，P為拋物線上動點，則|PF|+|PQ|的最小值為.

設計意圖：由例題出發，改變點Q的位置，定點Q在拋物線的外側，焦點F在拋物線的內側，不需要通過定義轉化，可以直接求解；與例1形成對比，引起認知沖突，揭示學生學習中的問題，引導思考例1用定義轉化距離的原因，是因為求動點到兩個定點距離之和最小值時，需要把同側距離(定點在動點的同側)轉化為異側距離(定點在動點的異側)，然后利用三角形的兩邊之和大于第三邊，當三點共線時距離之和取得最小值，提升數形結合思維.

變式2 拋物線y2=4x上一動點P到直線x=-1的距離為d，定點Q(1，1)，則d-|PQ|的最大值為.

分析：定點Q在拋物線的內側，直線在拋物線的外側，作圖(略)，運用拋物線定義將點到準線的距離轉化為到焦點的距離d=|PF|，d-|PQ|=|PF|-|PQ|≤|QF|=1.

設計意圖：例1和變式1都是求距離之和最小值問題，變式2引出了求距離之差的最大值問題，需要把異側距離轉化為同側距離，然后利用三角形中兩邊之差小于第三邊，當三點共線時同側距離之差取得最大值，激發逆向思維.

2 變式探究

教師提問1：以上是關于拋物線上的動點到定點或定直線的距離之和(差)的最值問題，同學們能否小組合作，探究在其他的曲線上是否也有這種最值問題呢？

學生探究1：其他圓錐曲線上的動點到定點的距離之和(差)的最值.

教師請學生上臺展示探究結果，整理如下：

圖1

教師提問2：上面的展示題還可以有其它變式嗎？

學生1：可以改變定點P的位置，由曲線外變為曲線內.

學生2：可以把左焦點換為右焦點.

教師提問3：這些都是很好的變式，那剛才例題中我們研究了拋物線上的動點到定點和定直線的距離之和(差)的最值，同學們在雙曲線、橢圓上已經研究了到定點的距離之和(差)的最值，那能不能考慮定直線呢？

學生探究2：圓錐曲線上的動點到焦點和到某定直線的距離之和(差)的最值.

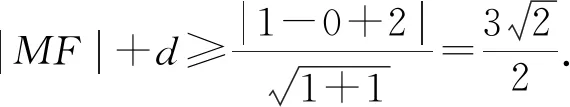
設計意圖：由動點在拋物線上變化到雙曲線、橢圓上，培養類比遷移思維，靈活運用圓錐曲線定義實現同側距離異側距離相互轉化；然后數形結合利用三角形中兩邊之和大于第三邊，可以求異側距離之和的最小值，利用三角形中兩邊之差小于第三邊，可以求同側距離之差的最大值，進一步提升學生的類比思維和數形結合能力.

教師提問4：動點如果在圓上呢？情況是否類似？

學生回答：圓上任意一點到定點或者定直線的距離最值可以轉化到圓心的距離與半徑的關系求解.

教師提問5：對，其實也是用了圓的定義轉化.那動點如果在直線上呢？請同學們畫圖試試.

學生畫圖后紛紛回答，這是初中學過的“將軍飲馬”問題.

設計意圖：通過改變動點的軌跡，追溯根源，找到此類題型的數學模型“將軍飲馬”，揭示知識間的聯系，減輕學生的學習負擔，激發探究興趣.

圖2

教師總結：前面的題目都是研究曲線上的一個動點的問題，下面我們來看兩道多個動點的問題.

分析：如圖2，雙曲線左右焦點F1,F2分別為兩個圓的圓心，|PM|≤|PF1|+2，|PN|≥|PF2|-1，所以|PM|-|PN|≤|PF1|-|PF2|+3=5.

圖3

分析：由漸近線方程可得b2=12，如圖3，由雙曲線定義得|MF|=2a+|MF1|，|MN|≥|MQ|-r(Q為圓心，r為半徑)，|MN|+|MF|≥|MQ|-r+2a+|MF1|≥|F1Q|+3=8.

設計意圖：涉及圓的多動點的距離和差最值問題，一般運用圓的定義，到圓上動點距離最值可以轉化到圓心(定點)和半徑的關系求解，進一步體會圓錐曲線定義在相互轉化中(動點轉化為定點、同側距離轉化為異側距離)的作用.

延伸探究問題：學生課后把雙曲線換為其他的圓錐曲線再進行探究.

3 教學反思

在單元復習教學中，從某個小知識點切入，通過改變題目條件，暴露學生解題中的疑惑點和易錯點，尊重學生的認知規律，順應學生的思維，通過教師的引導逐步深入，學生參與變式探究，對題型不斷深入挖掘，追根溯源，促進學生深度學習能力，鞏固和創新教學方法，有助于減輕學生的解題負擔，激發學生的探究興趣.