高速公路收費站車道功能及方向優化模型

宋浪，俞山川，王少飛，安文娟

(1.招商局重慶交通科研設計院有限公司，重慶 400067；2.哈爾濱工業大學交通科學與工程學院，哈爾濱 150090)

2019年起中國逐步加快推進電子不停車快捷收費的推廣應用，且根據《取消高速公路省界收費站總體技術方案》要求，未來實現高速公路開放式無站自由流收費。電子不停車收費(electronic toll collection,ETC)系統的便利性和快捷性促進其推廣應用，ETC用戶數和使用率正在逐步增加，但目前ETC的使用率不足以支持取消人工半自動收費(manual toll collection,MTC)車道，使得收費站ETC、MTC車道混合設置長期存在。故需結合收費站交通量、交通組成和ETC使用率，科學合理地設置收費廣場車道配置方案，以保證收費站通行效率。

姬楊蓓蓓等[1]以建設運營成本和延誤成本最小為目標建立優化模型，探討在不同流量和ETC比例下收費站的合理建設方案。楊濤等[2]根據車輛類型和不同支付方式服務時間修正得到車道的實際通行能力，以此實現建設期車道數優化計算。隨著自動駕駛技術的興起，未來需考慮高速公路自動駕駛車輛收費車道的設置，為此Yu等[3]探討不同自動駕駛車輛占比下收費站車道配置。以上研究探討的是建設期的車道配置方案，而運營期更多關注車道的開放數量和車道的使用功能。

林培群等[4]以收費站運營成本和用戶延誤成本最小為目標，研究收費站車道類型組合開放方案。錢超[5]等構建了包含跟馳和變道行為的收費廣場交通行為模型，并由此提出了收費廣場車道合理配置方案。Wang等[6]選取排隊長度作為收費站擁堵的評價指標，從而給出不同流量下收費站車道開放方案。Kim等[7]研究了收費廣場的最佳車道配置，并制定策略將車輛引導到排隊較短的車道。崔洪軍等[8]考慮運營成本和排隊成本，探討收費車道開啟方案。上述研究是一種車道功能優化方案，通過調整ETC/MTC混合車道的使用功能，以達到收費站整體通行效率最優，但并沒有突破收費站出口或入口的容量限制。還有學者針對收費站混合車道通行能力、幾何設計等方面展開了研究[9-12]。

近年來，隨著人民生活水平的不斷提高，居民節假日和周末定期選擇郊區旅游或回鄉的現象越來越明顯，使得一些臨近城區的高速公路收費站存在顯著潮汐現象，假期開始以出城上高速交通需求為主，假期結束以返城下高速交通需求為主。為此，部分收費站試點開設了“潮汐車道”的潮汐收費島，以緩解通行壓力，這屬于一種車道方向優化方案。

另一方面，為從根本上解決收費站擁堵問題，部分省市出臺了收費站擁堵免費通行政策，但由于相關研究較少，使大多數擁堵免費通行的規定較為模糊。崔志賓等[13]提出了考慮車道長度和車道面積折算的免費放行位置計算方法。而馮曉燕等[14]基于排隊論發現，當收費廣場排隊長度超過一定值，排隊車輛將無限排列下去，故免費通行位置的設置需參考此值。此方法確定的免費放行排隊長度值較大，適用于收費站開足收費車道仍存在擁堵現象的情況。但對運營單位為節約運營成本，故意未開足收費車道而導致擁堵的情況，需要同時考慮用戶延誤成本和收費站免費放行損失成本。

為此，借鑒城市交叉口逆向可變車道、借道左轉車道等車道控制思想[15-16]，通過動態調整收費廣場車道功能和切換車道收費方向，將其建立到一個統一的優化模型中，以適應不同流量場景，在不擴建收費廣場的情況下突破收費站出口或入口的容量限制，實現“智慧擴容”。并對比分析用戶延誤成本和收費站免費放行損失成本隨免費放行排隊長度閾值的變化情況，以通過平衡上述兩種成本給出收費站免費放行判定標準。

1 基本概念與車道配置過程

基于車道的收費廣場車道配置如圖1所示，從出入口各自行車方向的最右側往左連續設置相應的收費車道，使得在收費廣場中間車道形成雙向收費，車道的收費方向和使用功能可根據預測的交通量選擇配置。在運營期，通過動態調整MTC/ETC混合車道的使用功能，同時動態切換車道收費方向，以平衡收費站出入口交通需求，緩解單向擁堵，為“潮汐收費車道”和混合車道的開放提供理論依據。

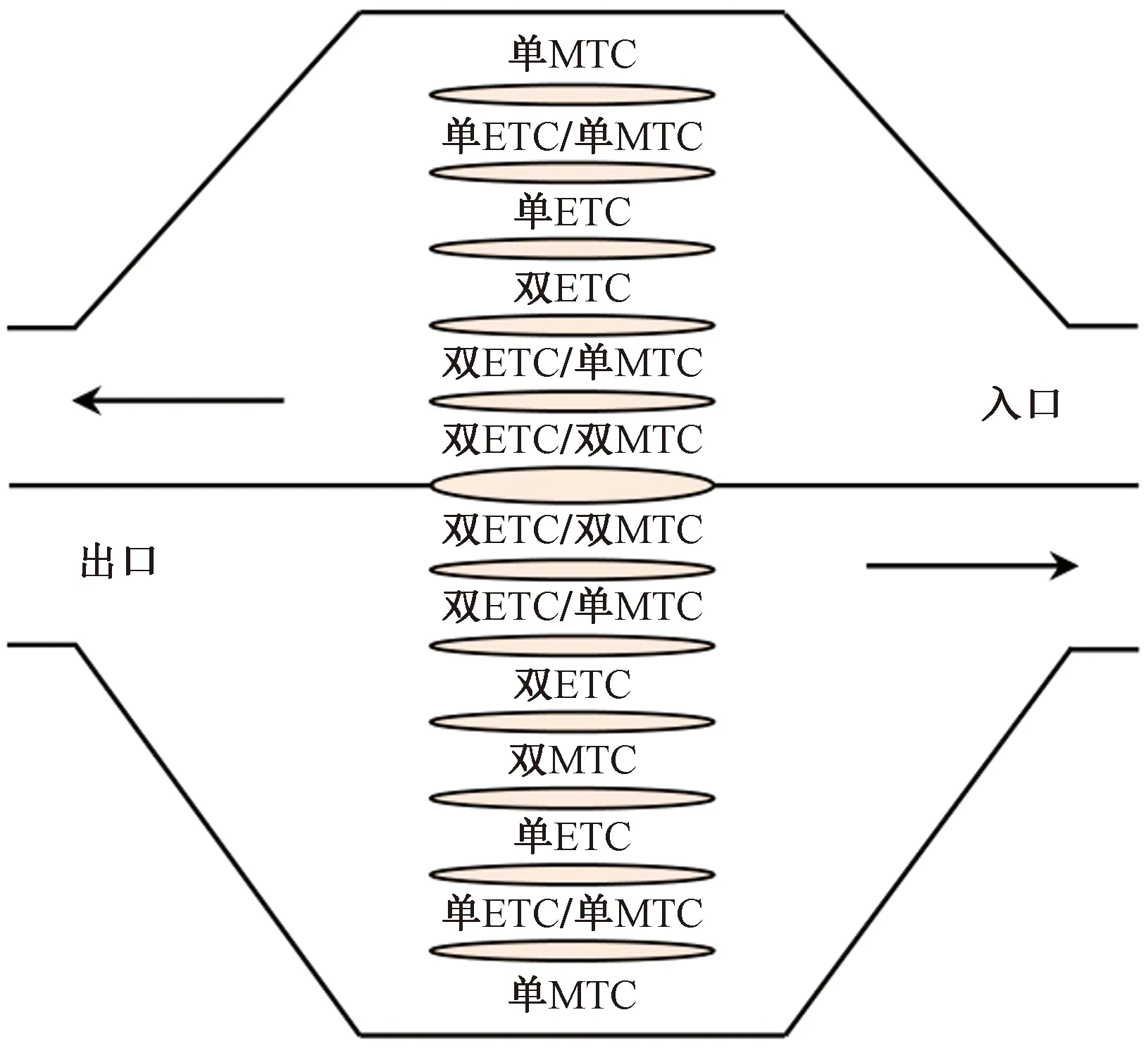
“雙”“單”分別表示車道是否可切換方向圖1 收費廣場車道布局Fig.1 Layout of toll plaza

2007年頒布的《收費公路聯網收費技術要求》給出了收費車道數計算依據，首先換算得到設計小時交通量，結合服務時間理論值，在設計要求的平均等待車輛數下，從車道數表格選取合適數值。但只適用單一收費制式，對于混合車道和雙向車道需進一步分析，基于車道的收費廣場設計階段車道配置過程如下。

Step 1根據《收費公路聯網收費技術要求》等，針對不同流量場景下的交通需求和ETC使用率，給出相應流量場景收費廣場出入口MTC、ETC車道數；

Step 2分別尋找所有流量場景中收費廣場、出口和入口總車道數最大值N、Nc、Nr，其中N作為收費廣場設計車道數，Ns=Nc+Nr-N為雙向收費車道數，Nc-Ns、Nr-Ns分別為單向出口、入口車道數。

Step 3分別尋找所有流量場景中出口MTC、出口ETC、入口MTC和入口ETC車道數最大值NcMTC、NcETC、NrMTC、NrETC，其中，Ncs=NcMTC+NcETC-Nc,Nrs=NrMTC+NrETC-Nr分別為出口和入口MTC/ETC混合車道數，NcMTC-Ncs、NcETC-Ncs分別為出口MTC、ETC單一車道數，NrMTC-Nrs,NrETC-Nrs分別為入口MTC、ETC單一車道數。

在設計階段車道配置基礎上，結合基于車道的收費廣場車道功能和車道方向控制思想，建立運營期收費廣場車道開放優化模型。

2 優化模型

2.1 目標函數

2.1.1 收費站運營成本

MTC車道運營成本包括設備運行成本、材料購置成本和人工成本[4]，材料購置成本按每輛車收費耗材計算。ETC車道運營成本即設備運行成本。則收費站運營成本計算公式為

Cjk=C′1+C′2λjk/yjk+C′3,?j;k=1

(1)

Cjk=C′4,?j;k=2

(2)

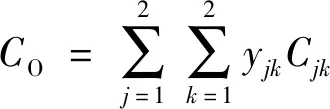
(3)

式中：C′1為MTC設備運行成本，元/h；C′2為材料購置成本，元/veh；C′3為人工成本，元/h，按每月工作22 d、每天工作8 h換算得到；C′4為ETC設備運行成本，元/h；Cjk為方向j功能k車道運營成本，元/h；CO為收費站運營成本，元/h；yjk為收費車道開放為方向j功能k的車道數；λjk為選擇方向j功能k繳費的交通需求，veh/h；j為車道方向，j∈{1,2}分別表示出口、入口；k為車道功能，k∈{1,2}分別表示MTC、ETC。

2.1.2 用戶延誤成本

延誤成本是車輛因排隊等待造成的時間損失費用，姬楊蓓蓓等[1]分為客車延誤成本和貨車延誤成本計算，并將多種車型延誤成本加權平均換算為單車平均延誤成本，楊濤等[2]同樣采用加權平均法將多種收費方式服務時間換算為單車平均服務時間。故用戶延誤成本計算公式為

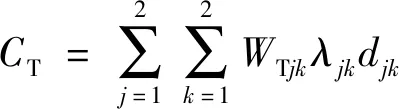
(4)

式(4)中：djk為平均等待時間，h；WTjk為車輛平均成本系數，元/(h·veh)；CT為用戶延誤成本，元/h。

2.1.3 收費站免費放行損失成本

中國多個省份都出臺了收費站擁堵免費通行政策文件，例如，《廣東省公路條例》規定“因未開足通道而造成在用通道平均五臺以上車輛堵塞的，應當免費放行并開足通道”；《江蘇省高速公路條例》規定“因未開足收費道口而造成平均十臺以上車輛待交費，或者開足收費道口待交費車輛排隊均超過二百米的，高速公路經營管理單位應當免費放行，待交費車輛有權拒絕交費”。通行費收取對運營單位有著重要作用，直接影響運營單位收費車道開放策略，需在優化模型中考慮。當出口各種車道平均排隊車輛數超過一定值，運營單位應免費放行，收費站免費放行概率和損失成本為

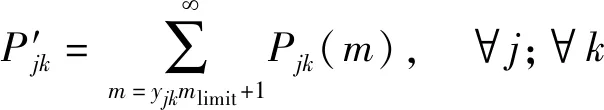
(5)

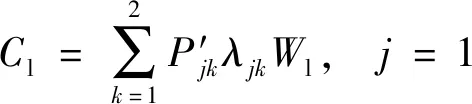
(6)

式中：Pjk(m)為方向j功能k中有m輛車的概率；mlimit為免費放行排隊長度閾值，veh；P′jk為方向j功能k中超過免費放行長度yjmlimit的概率；Wl為平均每輛車通行費用，元/veh；Cl為收費站免費放行損失成本，元/h。

優化目標為運營成本、用戶延誤成本和收費站免費放行損失成本之和，即

min(CO+CT+Cl)

(7)

2.2 約束條件

2.2.1 車道劃分約束

收費車道不能同時開放為出口和入口車道；為避免出入口車流相互交織，開放為出口的車道一定要位于出口側，開放為入口的車道一定要位于入口側；收費車道只有設計了各方向車道功能才能切換為此收費方向；各方向開放為各種功能車道數之和與切換為此方向的車道數相同；各方向開放為各種功能車道數不大于因車道設計限制允許開放的最大車道數。以上約束條件為

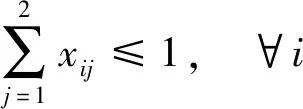
(8)

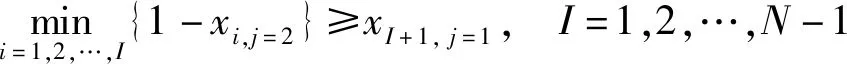
(9)

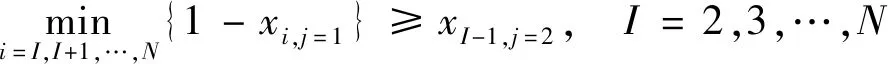
(10)

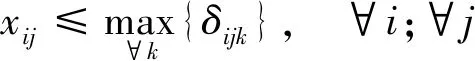
(11)

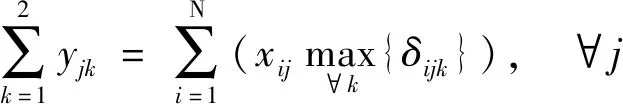
(12)

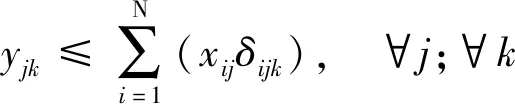
(13)

式中：xij為車道i是否切換為方向j，xij∈{0,1}，1表示是，0表示否；δijk為車道i是否可作為方向j功能k的收費車道，δijk∈{0,1}，1表示是，0表示否；根據收費車道具體設計輸入；i為車道編號，以出口方向最右側車道起往左分別編號{1,2,…,N}；N為收費廣場所有車道數。

2.2.2 排隊模型

采用數理統計中的M/M/N排隊系統模型來描述車輛通過收費站的過程，即

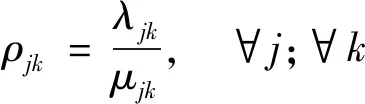
(14)

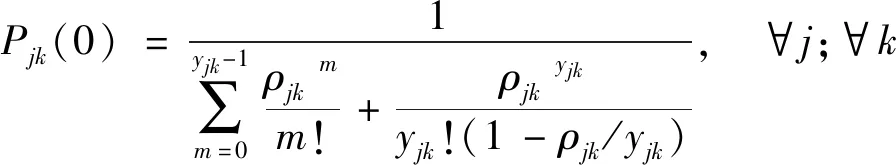
(15)

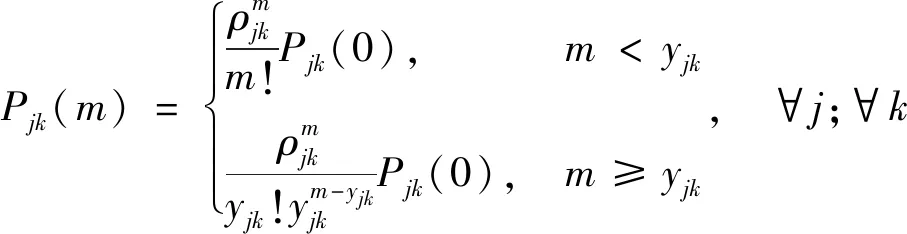
(16)

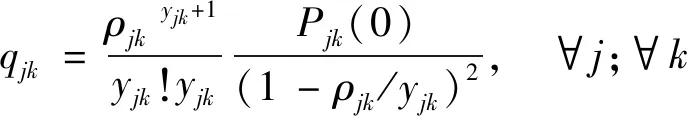
(17)

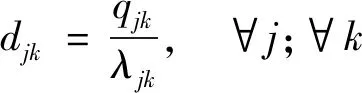
(18)

式中：ρjk為服務強度；qjk為平均排隊長度，veh；μjk為平均服務率，veh/h。

根據級數求和公式推導將式(5)變為

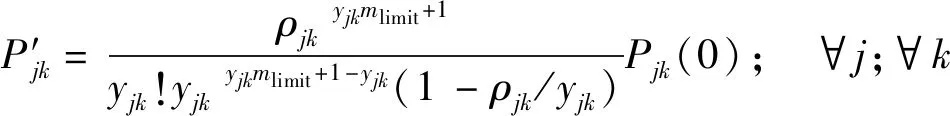
(19)

2.2.3 其他約束

為維持收費站穩定的運行狀態，根據交通流理論中的排隊論可知，每條車道的交通強度應小于1，及變量取值范圍為

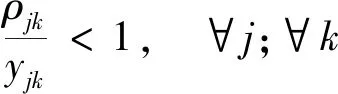
(20)

xij∈{0,1},yjk≥1,?i;?j;?k

(21)

2.3 討論

2.3.1 雙向收費車道設置問題

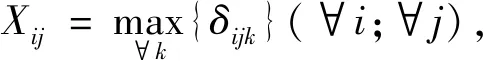
2.3.2 收費站免費放行判定標準

各省出臺的收費站擁堵免費通行政策是對運營單位進行約束，避免運營單位為了降低運營成本，未開足收費車道，造成在用車道排隊擁堵。為此，在交通強度為定值的情況下，據式(18)和式(19)，探討不同開放車道數中免費放行排隊長度閾值對免費放行概率和車輛平均等待時間的影響，如圖2所示。

由圖2可知，免費放行概率隨免費放行排隊長度閾值增加而降低，當閾值超過5～10 veh后，免費放行概率接近于零，此時閾值的增加對降低收費站免費放行損失成本作用較小，同時當閾值確定后，通過增加車道數，降低交通強度，可以降低免費放行概率，從而減少收費站免費放行損失成本。因平均等待時間隨閾值增加而增加，為平衡收費站免費放行損失成本和用戶延誤成本，根據收費站車道數和管控目標，免費放行排隊長度閾值宜在5～10 veh選取。

3 案例分析

3.1 基礎參數

選取如圖1所示的收費廣場作為研究對象，該收費廣場常規布局為出口方向7條車道，入口方向6條車道。為驗證本文優化控制的通行效益，選取車道不可切換收費方向的控制方案(簡稱“傳統方案”)對比分析。參考《收費公路聯網收費技術要求》和林培群[4]等參數取值，選取如表1所示的輸入參數。選取6種流量場景，根據優化模型確定收費廣場的最優車道配置方案，結果如表2所示。

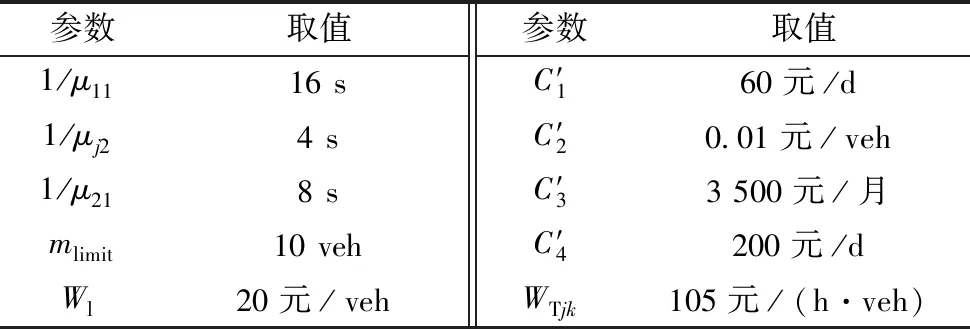
表1 基礎參數Table 1 Basic parameters

3.2 結果分析

利用VISSIM 9.0軟件對兩種方案仿真對比分析，調整隨機種子共仿真10次取均值作為評價依據[16]。如表3所示，在場景1、2中，兩種方案成本指標和延誤指標均相同，原因在于此時出入口交通需求較均衡，不需要切換車道方向便能達到系統最優。對于場景3、4出口交通需求大于入口，優化方案通過切換車道方向以分配更多的車道供出口使用，從而使得優化方案系統成本和總平均延誤小于傳統方案，提升了收費站通行效率。而場景5、6入口交通需求大于出口，優化方案則分配更多的車道供入口使用，以保證系統最優。由表2可知，因場景2、4、6車輛ETC使用率大于場景1、3、5，所以模型分配更多的車道作為ETC車道，同時降低了系統成本和總平均延誤，說明增加ETC使用率，能顯著提升收費站通行效率。

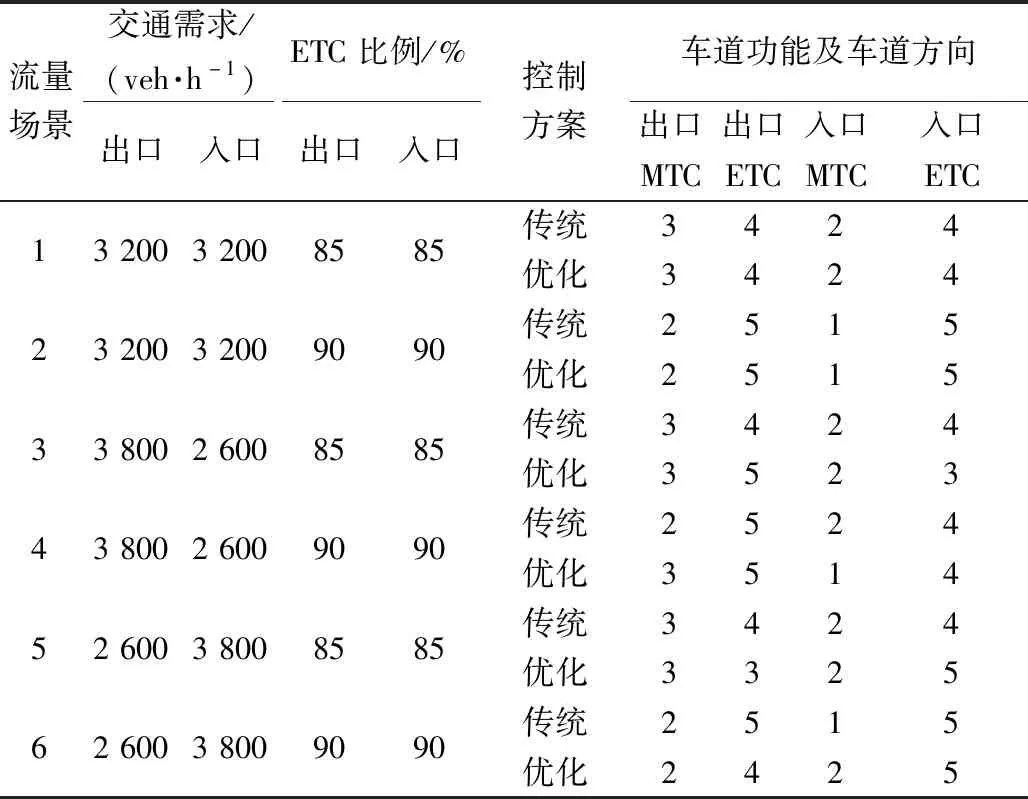
表2 不同情況下車道數的最優配置Table 2 Optimal allocation of lanes under different conditions

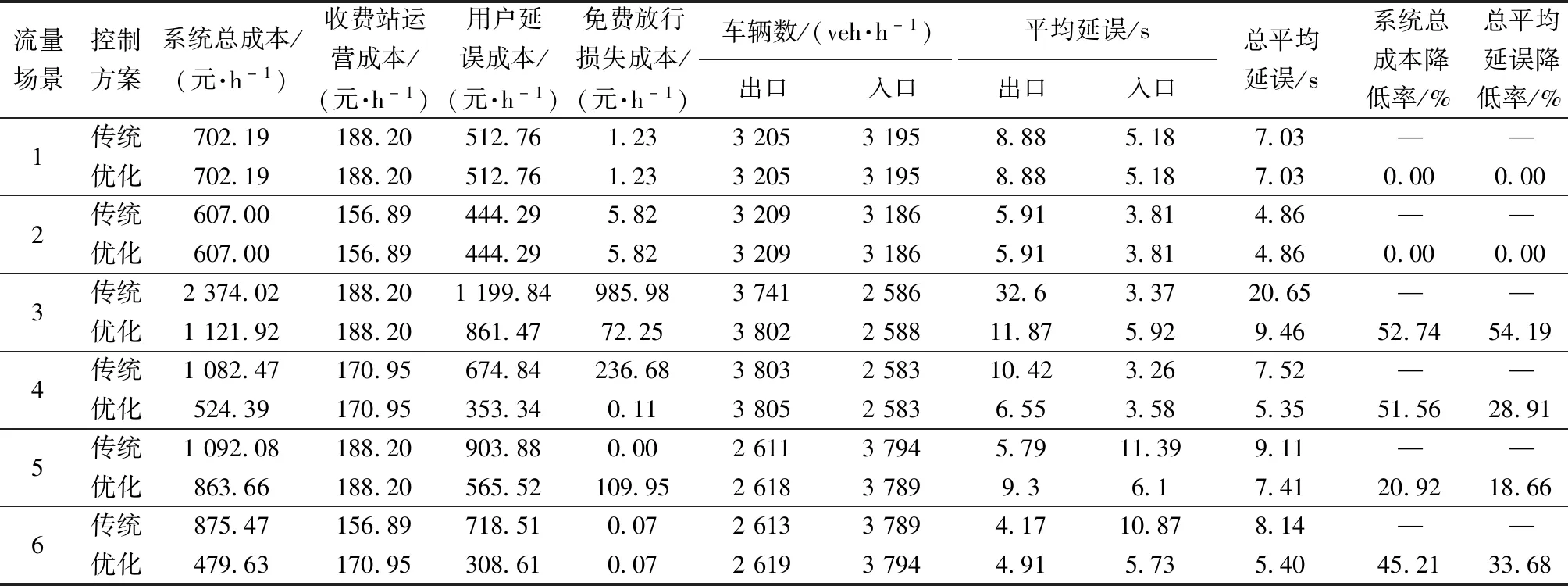
表3 仿真評價指標Table 3 Simulation evaluation indicators

4 敏感性分析

進一步分析兩種方案適用場景，探討ETC使用率和交通需求對系統成本的影響，ETC使用率取30%～90%，收費廣場總交通需求取3 000～6 000 pcu/h，優化方案所有車道均設計為雙向混合車道，傳統方案所有車道均設計為單向混合車道，其余輸入參數和案例分析相同。

如圖3所示，系統成本隨著ETC使用率增加而降低，且降低幅度逐漸減小，圖3(b)存在不滿足此規律的特例是由于決策變量為離散取值集合導致的。系統成本隨交通需求的增加而增加，且當交通需求較大、MTC使用率較高時，收費站通行能力不能滿足交通需求，使得模型沒有可行解。整體來看，優化方案系統成本普遍小于傳統方案，說明基于車道的收費站控制方法能夠提升收費站通行效率。同時，在部分流量場景中，優化方案存在可行解，而傳統方案不存在可行解，說明優化方案在不擴建收費站的前提下，通過車道控制突破了出口或者入口的容量限制，實現收費站“智慧擴容”。

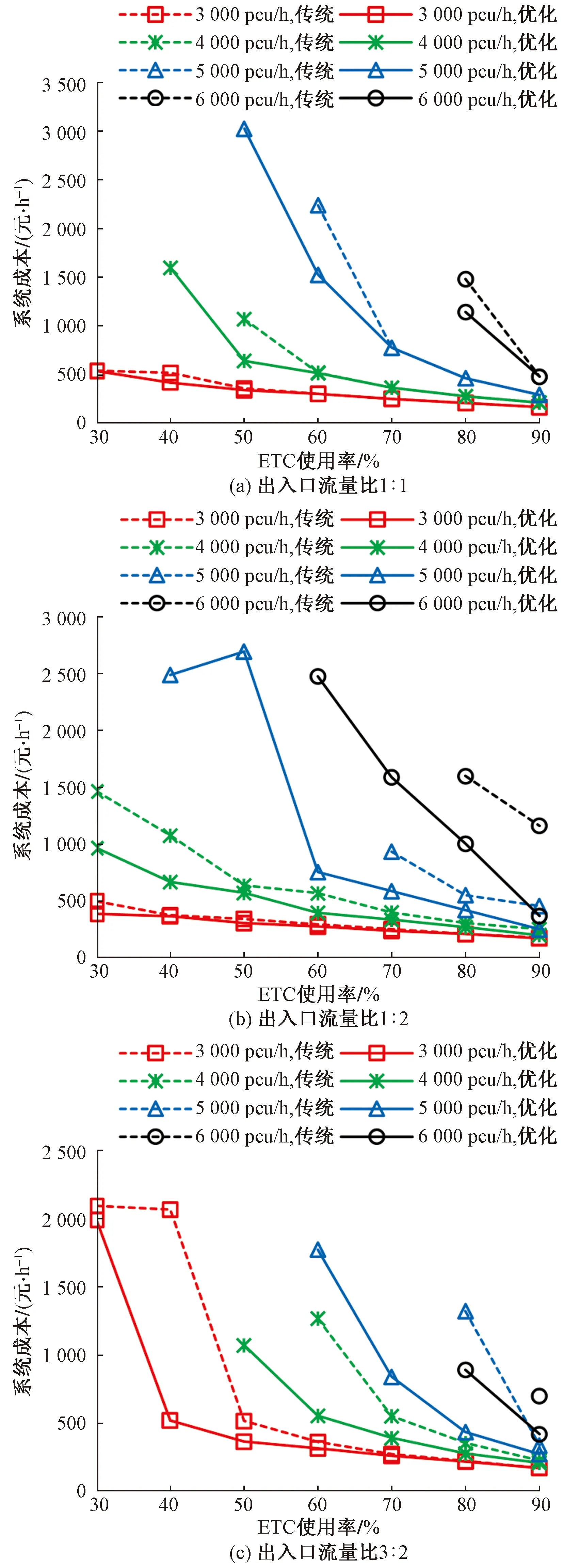
圖3 ETC使用率、到達流量和系統成本關系Fig.3 Relationship between ETC usage rate,arrival flow rate and system cost

5 結論

(1) 通過動態調整收費車道使用功能和切換車道收費方向，構建了基于車道的收費站車道功能及收費方向優化模型。通過討論發現：出口車道、入口車道需從各自行車方向的最右側往左連續設置，使得在收費廣場中間車道形成雙向收費；收費站免費放行排隊長度閾值宜在5～10 veh之間選取。

(2)通過案例分析和敏感性分析發現，優化方案通過動態調整車道方向和車道功能，以平衡出入口交通需求，降低了系統成本，提升了收費站通行效率。隨著ETC使用率增加、交通需求減少，系統成本隨之降低。優化方案系統成本普遍小于傳統方案，且適用的流量場景更廣。

(3) 在本文的后續研究中應重點關注中央分隔帶位置調整、車輛變道等微觀特征對收費車道通行能力的影響，以保證實際應用效果最佳。