考慮不確定性的航空發動機燃油計量組件典型故障仿真與特征分析
朱赟,徐瑀童,唐皓,朱昕昀
(1.中國航空發動機控制系統研究所,無錫 214000;2.南京航空航天大學民航學院,南京 210000)
航空發動機被譽為飛機的心臟,能夠為飛機提供推力和動力。然而發動機是一個極其復雜的系統,通常由大量的部件組成,每個部件都具有不同類型的故障模式,部件級別故障可能會引起系統故障,造成經濟損失,嚴重時還會導致飛行安全隱患[1]。因此針對航空發動機故障預測與健康管理技術的研究是一項重要任務[2],受到了學術界的廣泛關注[3]。
作為航空發動機控制系統的核心部件之一,燃油計量單元(fuel metering unit,FMU)以精確的流量向航空發動機提供所需的燃油流量[4],FMU的故障會影響航空發動機的工作性能,并限制其整體可操作性[5],所以其在役可靠性對整個發動機控制系統的性能起著決定性作用[6-7]。由于FMU必須應對高溫、高壓、強振動和快速變化的工作環境[8],極易發生故障。因此對FMU開展故障診斷技術的研究對于確保飛機機載系統的安全性和可靠性是非常必要的,受到了國內外學者的廣泛研究。文獻[4]基于相關向量機(relevance vector machine,RVM)算法建立了發動機組件逆模型,通過監測實際數據與模型數據之間的偏差對燃油計量組件進行了故障診斷。文獻[9]基于馬氏距離對燃油計量裝置的性能衰退進行了檢測,并結合隨機森林和支持向量回歸算法實現了剩余壽命預測。文獻[10]通過極端學習機建立逆模型,實現了對燃油計量裝置執行機構故障和傳感器故障的隔離與定位。文獻[11]通過提取故障特征作為健康指標,在考慮環境和結構不確定性的情況下,驗證燃油計量組件健康指標體系。
文獻[12]針對機理分析對發動機燃油系統關鍵部件(燃油計量裝置、壓差控制器、主燃油泵和增壓關斷活門)的健康指標選取策略進行了研究,可為燃油系統部件健康評估提供參考。然而,系統不確定性、測量噪聲和未知環境因素會影響故障診斷的可靠性[13],對診斷結果產生影響,在故障指標時應該充分考慮系統不確定性造成的影響。
因此綜合考慮燃油計量組件的不確定性因素,通過仿真模型的方式進行不確定傳播,提出了故障特征評估方法,為航空發動機故障預測與健康管理(prognostics and health management,PHM)系統健康指標的選取提供理論基礎。
1 FMU系統分析
1.1 FMU的結構
FMU的主要功能是根據飛行任務需求,按照發動機電子控制器發出的控制指令,以規定的流量向發動機燃燒室輸送燃油,從而滿足不同工況的燃油量需求[14]。主要由計量活門、電液伺服閥、位移傳感器、定壓活門、壓差活門等組件構成,圖1展示了一種典型的FMU結構原理圖。
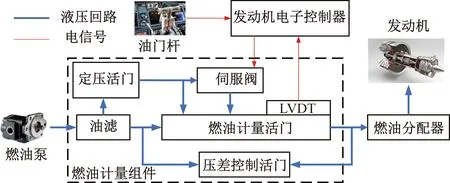
圖1 FMU結構圖Fig.1 Structure of FMU
計量活門控制通往發動機燃燒室的燃油流量,而壓差控制活門用來保持計量活門進出口的燃油壓差恒定,所以根據燃油質量流量,在壓差恒定的情況下,通過計量活門的流量只與計量活門的流通面積有關,這樣就能保證計后燃油由活門開度決定。燃油質量流量計算公式為
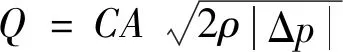
(1)
式(1)中:Q為燃油流量;C為流通系數;A為活門流通面積;ρ為燃油密度;Δp為活門前后壓差。
飛行員在駕駛艙中通過控制油門桿,將位置信號傳遞給(engine electronic controller,EEC),控制器輸出控制電流給電液伺服閥,伺服閥改變液壓油分布驅動計量活門閥芯移動,從而改變流通面積控制流量。閥芯移動過程中,通過線性差動位移傳感器(linear variable displacement transducer,LVDT)將計量活門位移信號傳遞給電子控制器,得到計量活門開度期望值與實際值的差值,通過控制算法計算后,輸出控制電流給電液伺服閥,電液伺服閥繼續調整閥芯位置,形成閉環控制,直到計量活門開度達到穩定值。
1.2 電液伺服閥
電液伺服閥作為關鍵部件對燃油控制系統的性能有著重要影響。由于其高精度、高集成度的特點,使得其容易發生故障,因此受到了廣泛研究。
在眾多類型的伺服閥中,擋板-噴嘴伺服閥在工業生產中被廣泛使用[15]。典型的擋板-噴嘴伺服閥結構如圖2所示。當控制線圈內有控制電流通過時,銜鐵產生電磁力矩驅動擋板發生偏轉,此時兩側噴嘴處可變節流孔液阻發生改變,這將會導致伺服閥閥芯左右腔室產生壓力差,驅使閥芯向對應方向運動改變流量分布。反饋彈簧根據閥芯移動距離產生反饋力矩到擋板處,直到在某一點達到受力平衡時閥芯不再運動。

圖2 噴嘴擋板式電液伺服閥結構Fig.2 Structure of nozzle baffle electro-hydraulic servo valve
2 FMU仿真建模與驗證
考慮到FMU系統的非線性和復雜性等因素,仿真模型基于AMESim軟件搭建。該軟件是基于直觀圖形界面的平臺,為用戶提供了可以直接使用的豐富的元件應用庫。目前,AMESim已經廣泛應用于液壓系統的故障診斷領域中[16]。
2.1 定壓活門模型驗證
定壓活門模型如圖3(a)所示,1端口為齒輪泵出口高壓油,2端口為出口定壓油。定壓活門閥芯受到彈簧力和出口油壓力的作用,當彈簧力與出口油壓平衡時,閥芯停止運動,出口油壓保持恒定。
定壓設計值為2×106Pa模型驗證時將齒輪泵出口高壓油壓力在10 s內由0提升至9×106Pa后階躍至5×106Pa,模擬齒輪泵不同工況,并且隨機改變節流孔直徑模擬后續組件的動作變化,齒輪泵出口壓力、節流孔直徑變化、定壓活門出口壓力如圖3(b)所示。可以看出,定壓活門的出口油壓穩定在設計值附近,符合設計要求。
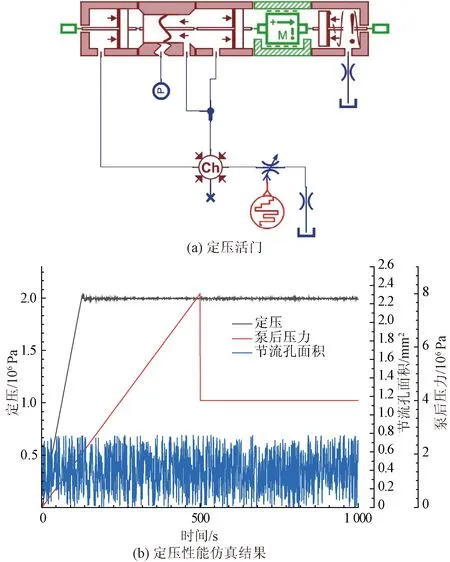
圖3 定壓活門模型與驗證Fig.3 Constant pressure valve model and verification
2.2 壓差活門模型驗證
壓差活門模型如圖4所示,1端口為齒輪泵出口燃油(計量前燃油),2端口為計量后燃油。定壓活門閥芯受到彈簧力、計量前燃油壓力、計量后燃油壓力的作用,當三力平衡時,閥芯停止運動,計量前后的燃油壓力差近似等于彈簧力,保證了計量前后壓差恒定。
壓差設計值為3×105Pa,模型驗證時與定壓活門類似,將齒輪泵出口燃油流量在8 s內由0提升至40 L/min后保持不變,將計量后壓力10 s內從0增壓至2×106Pa后保持不變,壓差始終保持在設計值左右,符合設計要求。
2.3 FMU整體模型驗證
由于FMU屬于液壓、機械、電氣組成的非線性復雜系統,各組件之間功能相互耦合,為滿足其工程精度要求,需要對模型進行整體性能驗證與評估。油門桿的輸入信號由注入高斯噪聲的線性信號源模擬,由于比例-積分-微分(proportion integration differentiation,PID)控制器結構簡單、易于實現、理論分析成熟等優點,用于計算伺服閥控制電流。圖5展示了FMU整體仿真模型。
通過不斷改變油門桿控制信號模擬發動機不同工況,圖6(a)顯示了控制信號和燃油計量活門(fuel metering malve,FMV)滑閥位移之間的對比圖,剖面的上升和下降斜率表現出良好的一致性。壓差和定壓如圖6(b)所示,經過0.5 s的穩定后,壓差在3.00~3.04范圍內波動,定壓在19.83~20.05波動,均滿足設計要求。因此,仿真模型已被驗證滿足工程精度要求。
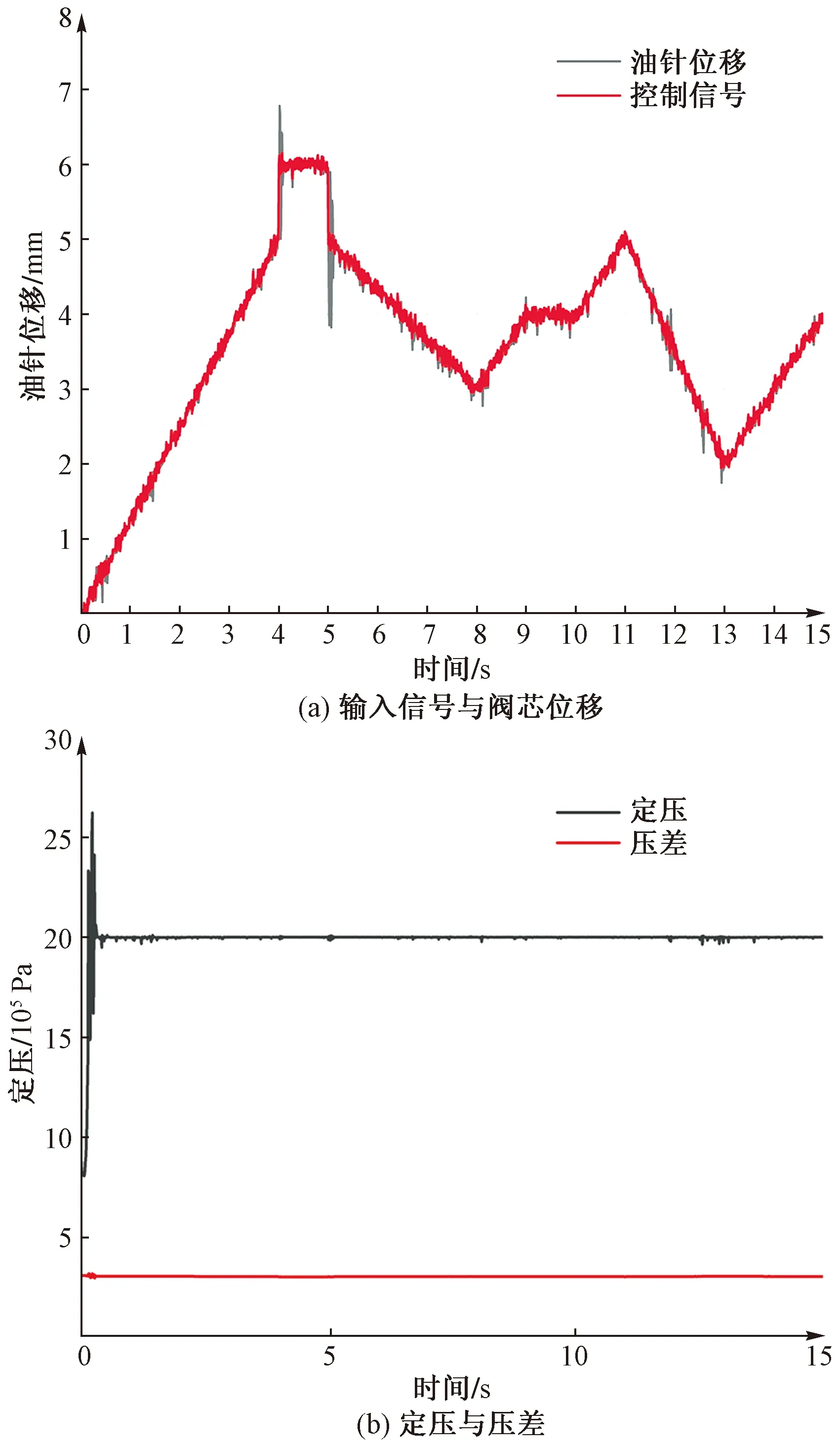
圖6 整體模型性能驗證Fig.6 Performance verification of FMU model
3 考慮不確定性的故障仿真
3.1 故障模式分析
通過對FMU以及電液伺服閥的結構及原理分析,參考以往的研究[11-17],結合專家經驗,選擇如下6種故障模式組成故障集,故障模式的介紹及仿真方法如表1所示。
3.2 不確定性參數
本文中,對于考慮不確定性的復雜系統的參數化模型,使用函數f表示[18]為
Yn×h=f(Un×k,ρ1,ρ2,…,ρp)
(2)
式(2)中:Yn×h表示模型的輸出矩陣;Un×k代表模型的輸入矩陣;n表示每次運行時采樣的次數;h表示輸出參數的個數;k表示模型的輸入參數個數,輸入參數是指在一次模擬的過程中不是常數的參數(如控制電流)。(ρ1,ρ2,…,ρp)表示模型中的p個不確定參數,不確定性參數定義為一次模擬過程中是常數,但是它的值在不同的模擬過程中不一定相同。
將研究對象的不確定參數分為3類。環境參數:表征系統的工作環境,如溫度;經驗參數:通過工程實踐總結得到的或者是規范標準推薦使用的,如作動筒直徑;故障參數:引起系統故障的參數,如:泄露直徑。其中經驗參數和故障參數都屬于結構參數。
由于不確定性,可以對不確定性參數概率分布函數(probability density function,PDF)隨機抽樣,從確定性模型中得到隨機輸出參數的分布。這種操作稱為不確定性傳播[19]。目前工程中使用較多、研究相對成熟的不確定性傳播分析方法主要基于概率論與統計方法[20-21]。采用基于概率的方法來度量變量的不確定性,通過給定變量的分布類型以求解不確定性傳播問題。
在這里,根據專家經驗和文獻[6]中的參數分布為依據,確定了9個不確定性參數的概率分布以及故障閾值,如表2所示。
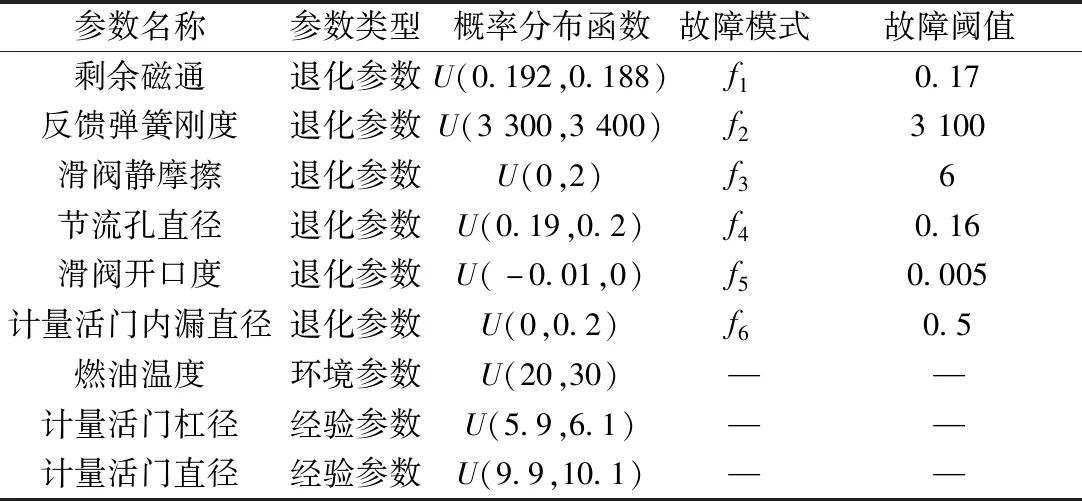
表2 不確定參數Table 2 Uncertain parameters
3.3 DOE
為了通過抽樣準確構建參數空間,有必要進行實驗設計(design of experiment,DOE)。試驗設計的思想是在完成實驗目標的基礎上,通過選取相對最少的樣本點,以節省實驗成本,并使獲取的關于未知空間的信息量最大化的方法。
拉丁超立方抽樣(Latin hypercube sampling,LHS)是一種流行的現代DOE方法[22]。拉丁超立方抽樣結合了隨機抽樣和分層抽樣的許多理想特征,與經典隨機抽樣(蒙特卡洛方法)相比,這種方法能夠通過重復更少的抽樣準確地重建輸入分布0。拉丁超立方抽樣包括如下步驟。
(1)將p維向量的每個分量都根據累計概率等分成n份,n為所需采樣點的數量,p為不確定參數的個數。
(2)從每一維的n個小區間中隨機抽樣構成n×p的初始矩陣。
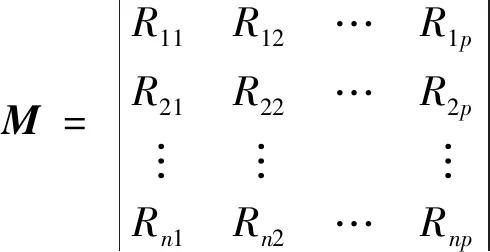
(3)
式(3)中:元素R表示從每個小區間中抽樣的隨機數。
(3)對初始矩陣中每一列的元素進行隨機排列,以模擬不確定參數的隨機組合,即
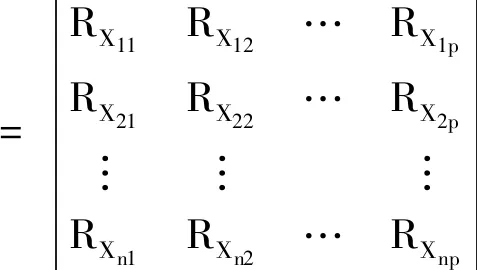

(4)
式(4)中:元素R的下標X11,X21,…,Xn1表示對M矩陣列向量元素的隨機排列,最終得到拉丁超立方抽樣矩陣,每一個行向量是一個p維試驗樣本,元素L表示實驗樣本中的不確定參數值。
根據得到的DOE矩陣,每次取一個p維試驗樣本,進行不確定性仿真,模擬實際工作環境下系統的不同工作狀況。
4 基于ROC曲線的特征評估
4.1 速度增益曲線
為了解決傳感器數量限制導致的故障信息不充分的問題,受伺服閥流量增益曲線的啟發,將LVDT位移信號與伺服閥控制電流相結合,得到速度增益曲線用于反映FMU系統整體性能。在表征伺服閥性能的不同方法中應用比較廣泛的是流量增益曲線,因為它能同時表現靜態和動態特性[11]。但伺服閥只是FMU中的一個子系統,因此流量增益曲線不能刻畫整個液壓機械回路的特性。所以本文以控制電流為自變量,利用計量活門的閥芯移動速度代替伺服閥出口流量作為因變量,獲取整個回路的速度增益曲線。
該曲線只需同時測量控制電流Icon和閥芯速度Vspool即可得到。Vspool由LVDT傳感器測得的閥芯位置Xspool差分得到。如圖7所示為正常狀態與6種故障狀態的速度增益曲線對比,可以看出故障與正常狀態的增益曲線之間存在不同類型的差異。
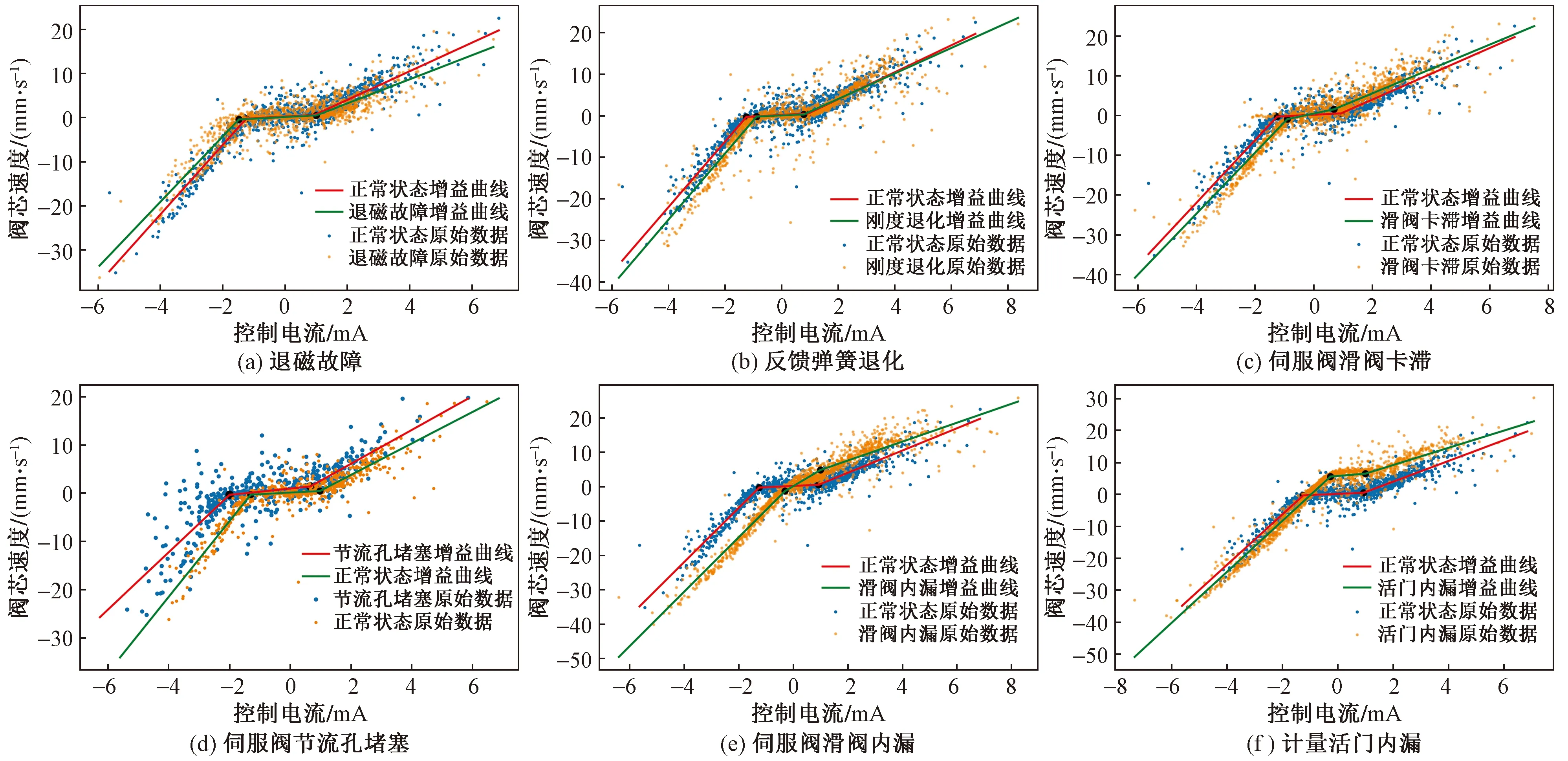
圖7 典型故障與健康狀態曲線對比Fig.7 Comparison between typical fault and health state curve
4.2 故障特征分析
基于速度增益曲線提取了FMU故障特征,表3中給出了故障特征和它們的定義,一些關鍵的特征在圖8中展示。根據不確定性傳播理論,由于不確定性參數的存在,即使是同一種工作狀態或者故障模式下,輸出的參數也會存在隨機性,這意味著更具輸出參數提取的故障特征值將會以分布的形式出現的,而不是特定值。因此,為了量化特征值對與故障診斷的潛力,定義了可檢測性指數(detectability index,DI)。DI的評估是基于受試者操作特征(receiver operating characteristic,ROC)曲線。ROC圖是一種基于分類器性能可視化、組織和選擇分類器的技術[23-24],被廣泛應用與機器學習、數據挖掘等領域。ROC圖是二維圖,其中真陽率(true positive rate,TPR)繪制在Y軸上,假陽率(false positive rate,FPR)率繪制在X軸上。ROC圖描述了收益(TPR)和成本(FPR)之間的相對權衡。但是ROC曲線只是分類器性能的二維描述,所以為了比較分類器性能,曲線下面積(area under the curve,AUC)作為單個標量值是一個重要指標,AUC越大,分類器平均性能越好。

表3 故障特征Table 3 Fault characteristics
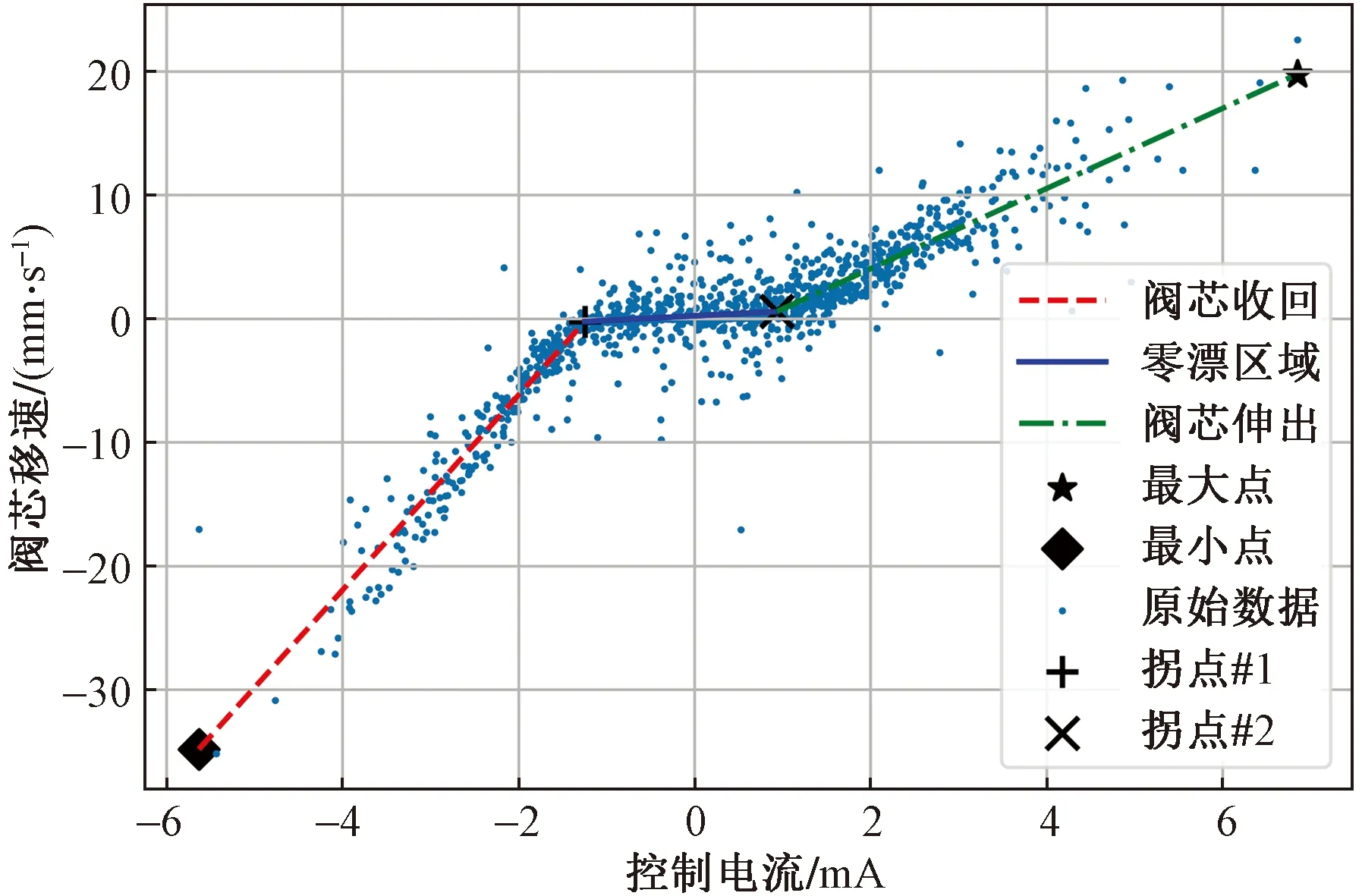
圖8 關鍵特征Fig 8 Key features
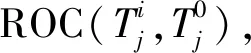
對于每一對故障特征/故障模式,DI表示特征對各類故障的檢測能力。DI的評估標準如下所示。
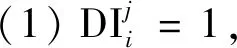

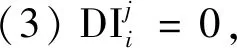

本文中標定點坐標為(0.05,0.9),表示特征對故障的檢測時,需要TPR>0.9,FPR<0.05才滿足檢測要求。
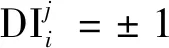
4.3 特征分析結果
以故障特征t16對故障集為例對評估標準進行說明。如圖9所示,
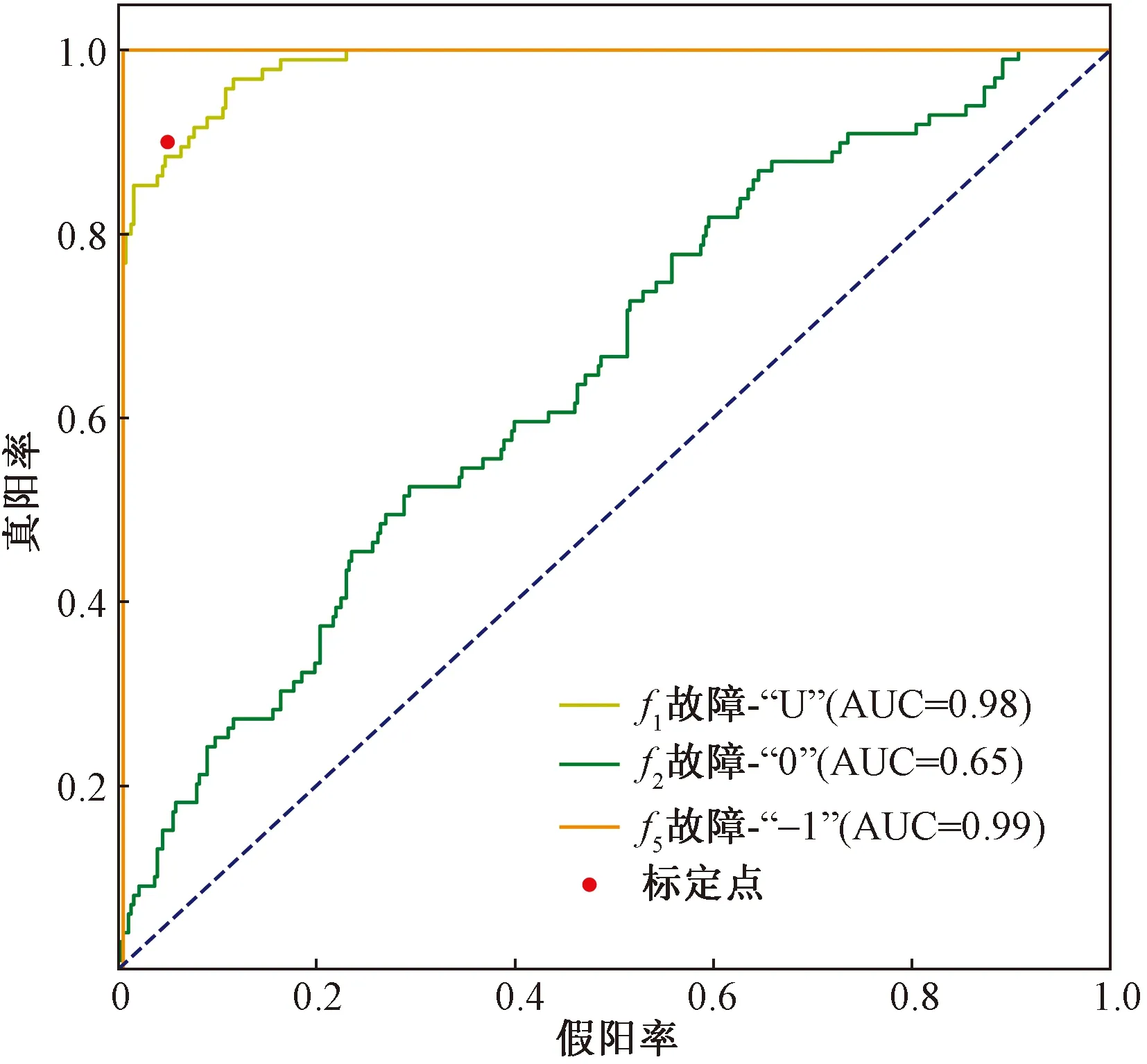
圖9 3類檢測指數對應的ROC曲線Fig.9 ROC curve corresponding to class 3 detection index
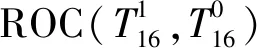
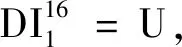
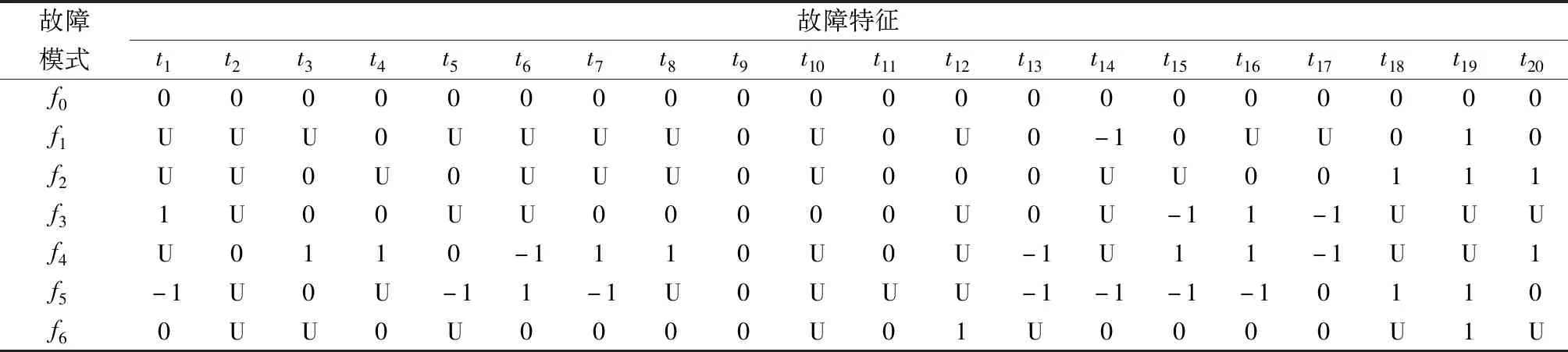
表4 檢測能力矩陣Table 4 Detection capability matrix
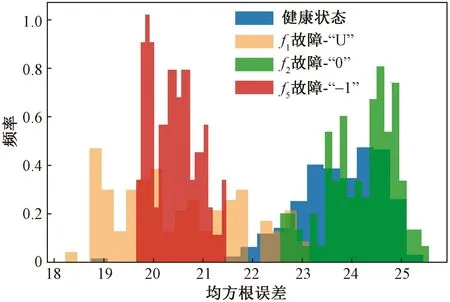
圖10 3類檢測指標對應的特征值分布Fig.10 Distribution of eigenvalues corresponding to three types of detection indicators
5 結論
以某型航空發動機的燃油計量組件為研究對象,考慮系統不確定性,面向健康管理技術開展了典型故障的特征提取與評估工作,得到了以下結論。
(1)基于AMESim搭建的FMU仿真模型具有較高精度,能夠滿足工程設計需求。
(2)考慮到系統不確定性時,使用拉丁超立方采樣方法構建參數空間進行仿真模擬,能夠得到接近真實工況下的系統工作數據,有效保證分析數據的可靠性。
(3)速度增益曲線能夠反映系統整體工作性能,通文中所分析的所有典型故障均能夠在曲線特征上有所體現,實現了在不額外增加傳感器的情況下對典型故障的間接檢測。
(4)本文提出的基于ROC曲線的故障特征評估方法,建立了故障特征對典型故障檢測能力的評價體系,為系統健康管理技術的開發提供理論基礎。

