立足實踐操作，發展演繹推理能力

祁倩倩

［摘? 要］ 推理是一種常見的數學思維方式，具有將抽象內容具體化，深化學生對知識本質理解的作用. 文章以“證明”的第一課時的教學為例，以教學分析為起點，結合對“觀察到的結論并不一定是正確的”“說理是確定實踐結論的關鍵”兩部分內容的授課，具體談談在初中數學教學中，該如何立足于實踐操作，發展學生的演繹推理能力.

［關鍵詞］ 證明；演繹推理；思維

“數學是思維的體操”，是促進學生邏輯推理能力發展的學科. 邏輯推理能力是指學習者能敏銳地分析并思考所遇到的問題，迅速掌握問題核心，并在短時間內做出正確反應的能力. 邏輯推理包括演繹推理、歸納推理與類比推理三種，本文著重探討的是演繹推理. 這種推理方式以“一般性”為前提，通過推導獲得具體結論，它在一慣性與嚴密性上與其他兩類推理方式相比，具有一定的獨特性.

教學分析

《義務教育數學課程標準（2022年版）》（下文簡稱新課標）將數學核心素養定義為學生必須具備且能適應其終身發展與社會需要的關鍵品質與能力，并明確了六大素養，提出了“四基與四能”“三會”等要求［1］. 實踐證明，數學實踐操作以“做”為支架，讓學生通過動手動腦自主發現一些數學結論，同時教學實踐操作具有顯著的直觀性，便于學生理解核心知識，可以取得口頭教學所無法比擬的教學效果.

數學實踐操作主要以問題為起點，將結論設為操作的最終目標，是展示知識形成過程的一種教學活動. 其內容選擇并不拘泥于教材，還可以源于生活，是數學課程必要的補充. 學生在數學實踐操作中，除了能直觀地看到知識本質，體悟數學思想方法，還能積累學習經驗，為后續研究奠定基礎［2］.

學習本節課之前，學生已經具備了一定的合情推理能力（通過探索發現結論），在此基礎上培養他們的演繹推理能力具有較強的可操作性. “證明”的第一課時，教學目的在于讓學生發自內心地感受“證明”的強大力量，為學生演繹推理能力的形成奠定基礎.

教學實錄

1.獲得的結論并不一定是正確的

縱然實踐操作有著得天獨厚的教學優勢，我們通過實踐操作所獲得的結論并不一定是正確的，這就需要我們具備敏銳的洞察力，在演繹推理的過程中學會辨析. 本節課中，師生首先共同回顧“三角形內角和”的操作證明過程，在學生提出“量、剪、拼”的方法后，教師邀請一名學生到黑板上快速用三角形模板進行實操演示.

教師總結并板書：實踐操作是認識新事物的重要手段之一.

師：通過操作所獲得的結論，通過感官系統所感知到的結論一定都是正確的嗎？

生1：不一定.

師：請舉個例子說明一下.

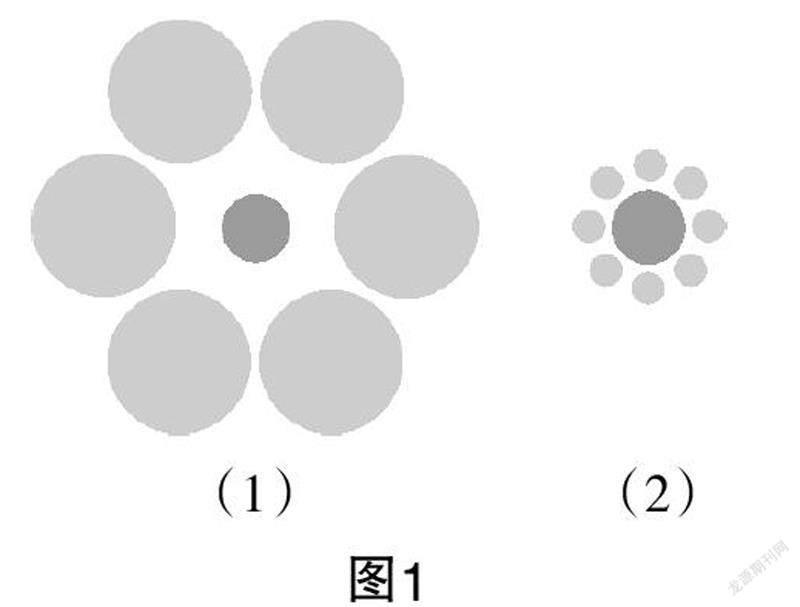
演示1 如圖1，一位學生畫了兩幅大小圓的圖. 觀察兩幅圖，學生一致認為圖1（2）中間的大圓比圖1（1）中間的小圓大. 當畫圖的這位學生將兩幅圖疊合在一起時，大家驚訝地發現圖1（1）中間的小圓竟然大于圖1（2）中間的大圓.

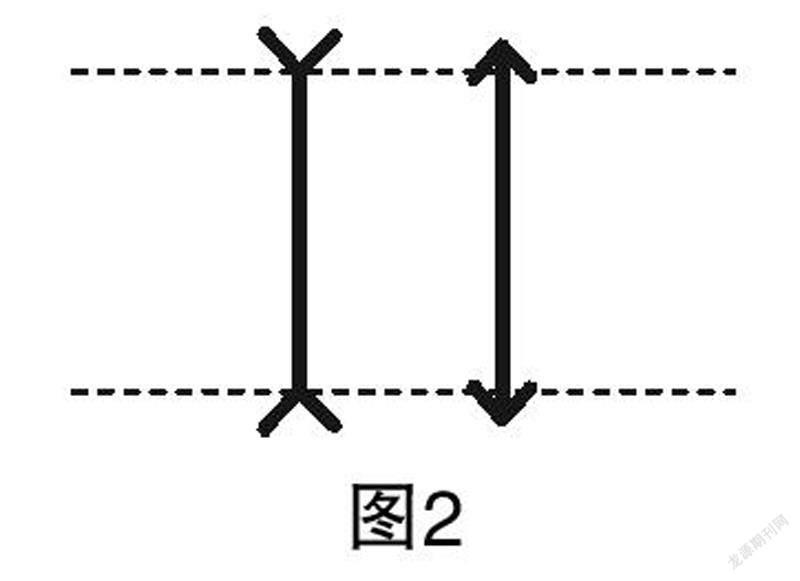
演示2 如圖2，判斷兩根線段的長度是否相等. 在沒有虛線的情況下，大家都認為前面那根線段比后面那根線段長，而實際上兩根線段一樣長.

師：通過以上兩個例子，我們能獲得什么道理？

生2：通過肉眼觀察所得到的結論，有時候受參照物的影響會出現偏差.

師：很好，那么我們在數學實踐操作過程中所獲得的結論是否可靠呢？現在請大家做如下操作，將一個邊長為8 cm的正方形，剪拼成一個5 cm×13 cm的長方形.

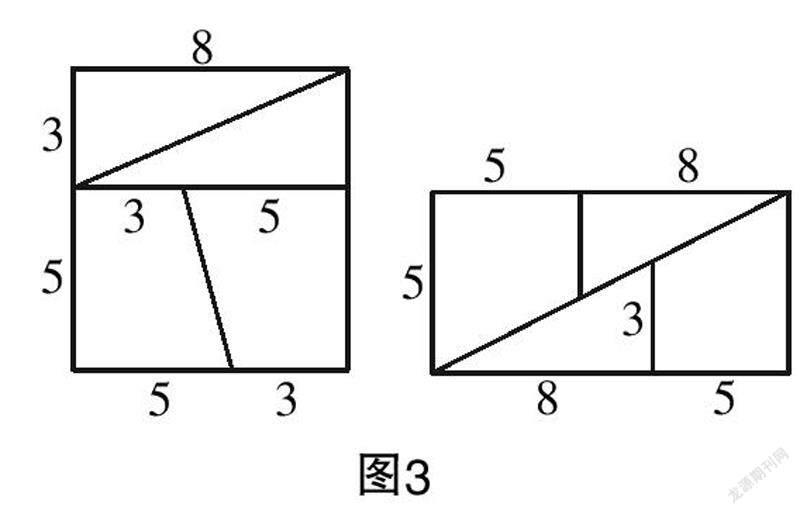
演示3 如圖3，學生以小組合作學習的方式進行畫圖、剪拼. 實驗結束后，學生發現了一個問題，即正方形的面積為8×8=64 cm²，而拼成的長方形面積卻是5×13=65 cm2，那么這多出來的1 cm2是從哪里來的呢？

教師為學生提供了一張邊長為80 cm的大正方形，通過剪拼后，學生恍然大悟，原來拼成的長方形中間存在一個縫隙. 至此，問題就迎刃而解了.

教師板書：實踐操作所獲得的結論并不一定是正確的.

三個實例，刷新了學生原本對實踐操作的認識. 不少學生原本認為自己親眼所見、親耳所聞的一定是真理，而事實告訴他們：參照物不一樣，感官對同一信息會產生不一樣的反饋. 如何避免這種問題呢？需進行進一步說理與證明.

2. 說理是確定實踐結論的關鍵

如果說實踐操作是說明事實的過程，那么論證是驗證該事實是否正確的重要渠道. 反觀之前所接觸過的“論證三角形內角和”問題，學生通過操作獲得相應結論后，教師還會對為什么三角形的內角和為180°進行補充說明，此時的補充說明就是說理的過程.

教師板書：實踐操作所獲得的結論，需要經過論證才能確定其是否成立.

例1 某小區有一條長、寬分別為a m、b m的長方形草坪，現在準備在這塊草坪中間鋪一條鵝卵石的小路，預計路寬為1 m. 設計師提出了直路（見圖4）與曲路（見圖5）兩種方案，面對這兩種方案，工程師產生了爭執.

甲工程師：直路的方案比曲路方案好，因為直路比曲路省材料.

乙工程師：我認為曲路的方案好，有藝術感，而且曲路與直路的面積是一樣的，因此耗材也一樣.

師：你們認同哪位工程師的觀點？說明理由.

學生經思考后，提出曲路確實更具美感，適合用在小區內. 但直路與曲路的面積是否一樣，需要研究一下. 從兩條小路的面積來觀察，圖4的直路面積為1×a=a m²，但圖5中曲路的面積該怎么求呢？學生一致認為這是個棘手的問題.

教師要求學生通過小組合作的方式來探尋答案. 從巡視中發現，學生無從下手，于是教師適當地加以點撥：長方形草坪的面積為ab（m²），除去草坪部分的面積就是路的面積，如果從路的角度無法獲得結論，就從草坪面積著手.

在教師的點撥下，立即有學生發現路的寬度恒為1，草坪被路分成了兩半. 若將兩塊草坪的面積合并（學生操作，剪拼），則得出以下結論：S_曲路=ab－a（b－1）=a m². 由此可確定曲路與直路的面積是一樣的，也就是說乙工程師的意見是正確的. 此即為說理的過程.

師：本題的解題關鍵在于求曲路面積時，要關注到剩下草坪的面積與路的面積的和是ab. 解題時，思維不要局限于求路的面積，還可以轉化為求草坪的面積. 這體現了一種重要的數學思想方法“轉化思想”，應該說這個結論是本節課的一個重要收獲.

教師板書：轉化思想.

師：剛才，我們用說理的方式證明了在幾何圖形中兩條不同形狀小路面積的關系問題，從中大家都感受到了說理在數學學習中具有的力量. 其實，說理在數學學習中無處不在，接下來，我們通過一個代數的例子來感受說理對數學學習的影響.

例2 教師用PPT展示代數式：x²－2x+2.

師：在這個代數式中，當x取值發生變化時，值也會相應地發生變化，但究竟是怎么變化的呢？我們都知道x可以取的值太多了，我們該從什么角度去取值并判斷結論的變化范圍呢？

生1：可以隨便取幾個試試，或者從正數、負數與零中各取幾個試試.

師：那就請大家分別從這幾類數中取值看看.

學生自主取值存在一定的個體偏好，如一位學生分別取了2，6，10， 0，－2，－4，－8. 這位學生所取的值，都是整數且為偶數. 真是無心插柳柳成蔭，這種取值方法是教師沒有預設到的，因此產生了不少意料之外的猜想.

教師將這位學生的取值投影到黑板上，并要求大家建立一個表格（見表1），將數據填入表格后進行分析.

師：大膽的猜想是獲得偉大發現的基礎. 現在請觀察你們填寫的表格，并對x²－2x+2的取值范圍提出相應的猜想.

在教師的鼓勵下，學生經過分析獲得如下猜想：①x²－2x+2的值必然為偶數；②該式的值必然為正數；③該式的值必然為整數；④x²－2x+2的值必然大于等于2，等等.

教師要求學生辨別這些猜想的正確性. 有學生提出，可以從反面進行論證，即舉反例.

師：既然提到了舉反例的方法，現在請大家再取幾個特殊值來看看以上猜想是否正確.

生2：當x為1時，該式的值為1. 此時，新的猜想又出現了，即x²－2x+2的值必然大于等于1.

師：這個結論是否正確呢？咱們再來取值看看.

此時，學生提出了困惑：x的值不可能全都取到呀，這怎么判斷呢？

問題又回到了原點.

師：如果從完全平方公式著手分析呢？

生3：將式子x²－2x+2進行變形可得（x－1）²+1，從這個式子來看，x可以取任意值，且（x－1）²≥0，此時問題也就迎刃而解了，即（x－1）²+1≥1.

師：說理是驗證操作所獲得的結論是否正確的重要方式，這也是下節課我們要著重研究的問題——證明.

此時，學生被說理的力量深深震撼，通過式子的轉化與演繹推理方法的應用，答案浮出了水面. 此過程，教師順應學生的思維，強調：判斷一句話是錯誤的可以從“舉反例”的角度去證明. 判斷一句話是正確的則可以從“嚴密說理”的角度去證明［3］.

教師板書：實踐操作得到的結論，離不開說理論證的過程.

教學思考

1. 結合實情調整教學順序

本節課教學從預設到生成并沒有完全遵循教材內容的順序，而是結合新課標所提出的“引導學生從合情推理到演繹推理發展”的要求，根據學生的實際認知水平進行了教學內容的調整. 本節課的重點放在“為什么要說理”，也就是進行演繹推理的理由上. 此過程為觀念形成過程，對后續學生的學習具有重要影響，因此教師耗費了大量的時間與精力在這個問題上.

事實說明，在解決了“為什么要說理”的基礎上引導學生充分感受證明的力量是正確的選擇，一節課下來，演繹推理的重要性與證明的力量在每個學生的腦海中生根發芽. 因此，結合實際情況微調教學順序，不失為一種良好的教學方式.

2. 結合課標調整教學方案

新課標的落地，引發了教育界的一股研究熱潮，尤其是“三會”要求的提出，讓廣大教育工作者不得不思考接下來的教學方向與方案. 究竟該如何才能讓學生通過課堂教學“會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界”？

研究發現，教師應用現成的導學案、教案與課件等，疏于深入思考，會導致教學流于形式，學生也無法感受到教師的良苦用心，更無法做到“三會”.

本節課，從教學內容上來分析，主要有三個模塊，分別為：①引導學生認識到實踐操作是認識一般事物的基本手段；②帶領學生感知，實踐操作所獲得的結論并不一定是正確的；③讓學生體驗，通過實踐操作所獲得的結論只有經過說理的過程，才能確定其是否成立. 其中，說理存在兩種方式，一種為舉反例，還有一種為步步有據.

因此，教師制訂在教學方案時，需從以上幾部分內容著手進行分析，并結合學生的實際認知水平，而非不加思考直接取用現成的課件. 基于學生實際情況，在本節課中筆者將前兩個模塊合并在一起教學，使得課堂充滿靈氣.

3. 結合預設促進課堂生成

課堂預設與生成是相輔相成的關系，因為學生的思維是動態變化的，所以真正的課堂是動態的. 教師只有在課前做好充分預設，才能在課堂上遇到“意外”時，靈活地采取應對措施，讓課堂充滿智慧. 這種狀態下的課堂能有效促進教學相長.

探討x²－2x+2的取值范圍時，雖然教師做了精心預設，但學生特殊的取值，出乎教師的意料. 此時教師并沒有避開這位學生特殊的取值，而是順應學生思維往下探討. 這種隨機應變的能力是教師綜合素養的體現，也是尊重學生的體現，學生在此過程中充分感知到證明的作用與力量.

綜上，在本節課的教學中，教師沒有完全照本宣科，也沒有急于求成地簡單告知，而是讓學生親身經歷了實踐操作后思維的發生發展. 師生通過幾個實例證明了“實踐操作所獲得的結論并不一定是正確的”，這個觀點不僅對學生數學學習具有深遠的影響，而且對于學生的“三會”也有重要影響. 本節課，學生充分認識到演繹推理的重要性，通過推理觸碰到了知識的本質，而課堂也因為演繹推理，更具內涵.

參考文獻：

［1］ 中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］. 北京：北京師范大學出版社，2022.

［2］ 董林偉. 初中數學實驗的理論與實踐研究［M］. 南京：江蘇科學技術出版社，2013.

［3］ 史寧中. 試論數學推理過程的邏輯性：兼論什么是有邏輯的推理［J］. 數學教育學報，2016，25（04）：1-16，46.