改進的電壓檢測極值中值濾波算法設計

李志鵬，王青燕

(1.江西財經大學，江西 南昌 330013；2.江西經濟管理干部學院)

0 引言

電壓數據的檢測及過濾目前有多種方法，主要有離散傅氏變換算法[1]，快速離散傅氏變換算法[2]，一點采樣算法、兩點采樣算法，積分交流采樣算法等。電壓檢測會有誤差，設計算法的目的是盡可能地減少檢測上的誤差[3]。每種算法有各自的優缺點，如快速離散傅氏變換算法可獲得比較全面的測量數據,但此算法計算結果較多，對一個周期中相同間隔采樣點數有很大的要求，內存占用大[4]，中間變量比較容易溢出，采用固定點運算實現困難；有學者針對數據過濾的問題，提出用中值濾波的方式，也有學者對中值濾波算法進行了改進函數過濾[5-7]，目的是減小數據的方差[8]，降低污染數據的比例[9]，提高數據的可靠性。

極值中值濾波的規則：某點的電壓值與附近點的電壓值相差很大，這一點可歸屬為極值點，如果相差不大，則表現為正常電壓值，若極值點表示為min{}或者max{}，正常點數表示為sta{}，則檢測到的數據點an可以表示為：

此算法的好處在于可將變化速度快的數據分離出來，將正常數值的數據存放到設置好的預留區。但此算法存在不足之處，若外界的非線性設備使用的頻率高，對電路產生的沖擊電壓可能波及較大區域。采集器收集數據時，一個周期內可測量多個數值點，數據是否有效無法判斷。基于上述問題，對算法進行了改進。通過數據顯示，改進的極值中值濾波算法，刪除更多波動性大的數據，保留的數據方差波動性更小。

1 中值濾波算法的原理

濾波就是過濾不合理的波值，在電壓應用中，非線性用電設備的瞬間上電、斷電，對電壓的沖擊，都會造成電壓諧波瞬間變化幅度大，若此刻電表正好采集到，電壓采集的數據將造成巨大的誤差，因此，濾波算法是很有必要的。在濾波算法中，現在已經有很多成熟的算法。按照數學原理，標準電壓的函數是正弦或者正弦平移變換的曲線，但在實際中，電壓波形曲線并不會嚴格符合標準。對數據的采樣造成較大誤差。

基于采樣值的不穩定性，有人提出了中值濾波算法，中值濾波算法實際上應用數學原理，采樣的點數據存放到系統中預留的存儲區，以備調用，采集模塊負責采集數據，但無法辨別數據的有效性，中值濾波的原理是對這些采集的數據進行分組，再對每個組內的數據進行由小到大或由大到小的排列，排列好之后取中間的部分。

已{X1,X2,X3,X4,X5,…,Xn}這組數據為例，它的中值M公式為：

其中，{a1,a2,a3,a4,a5,…,an}數列為{X1,X2,X3,X4,X5,…,Xn}數列由小到大排列的順序列。采集器采集數據，加載到數列{X1,X2,X3,X4,X5,…,Xn}中，如采集到的電壓值為{501,203,305,210,232}，則對它們由小到大的排列順序為{203,210,232,305,501}，中值M=232，這一組數據的中值可作為這組數據的標準值，轉存到中值數據區。

2 改進的算法設計

⑴改進的算法的分析

對于極值中值濾波算法，其不足之處在于不能更好地辨別一段區域內的誤差數值，基于上述問題進行了改進。一般電網都是遵循六個基本標準值（KV），公用電網的電壓標準值如表1所示。

表1 公用電網諧波電壓表

公共網絡的電壓值都在上述圖中，在預先設計好的數組中保存這些電壓值：

{0.38,6,10,35,66,110}

通過A/D采樣模塊，將采集的數據，與之對應。這種算法的設計首先設置好UN(電壓標準值)，設置參數自動檢測電網電壓中符合對應的電壓值，再由內部函數自動設置好相應的參數。可用線性規劃法設置對應的電壓值，以{0.38,6,10,35,66,110}為例，相鄰兩個電壓值組成坐標，由最后一個和第一個電壓值組成坐標，則對應坐標為：(0.38,6)，(6,10)，(10,35)，(35,66)，(66,110)，(110,0.38)，形成坐標后，連接相鄰兩點，形成線性規劃范圍圈，再取兩次電壓測定的數值，形成一個坐標，若坐標落在范圍圈內，則保留數據。再重新取采樣的兩個電壓值組成坐標，以此類推下去，直到采樣到落在范圍圈里的電壓值，兩次采取的電壓值通過采用均方差方法，積分得到電壓值，以便減少數據誤差。采用的公式為：

其中，N的數值為采樣次數，ui為每次測得具體數值。

本算法的關鍵是如何設置范圍圈，應用的理論是線性規劃法，兩點之間可以確定一條直線，例如A點坐標為A(x0,y0)，B點坐標為B(x1,y1)，則確定的直線方程公式如下：

⑵改進的算法的設計

第一步：確定六條直線,分別為A{(0.38,6)，(6,10)}，B{(6,10)，(10,35)}，C{(10,35)，(35,66)}，D{(35,66)，(66,110)}，E{(66,110)，(110,0.38)}，F{(110,0.38)，(0.38,6)}

化簡后，再用線性規劃的理論，列公式如下：

其中，x表示自變量，y表示因變量。

如此，圍成一個范圍圈，即便非線性用電器的長期使用，致使電壓出現的采取數據不準也會排除在外，這些直線組成區域圖形如圖1所示。

圖1 線性規劃范圍圈

采取的電壓值可以用此辦法將數據確定在范圍內，如果是在范圍外，可以再取兩次數據，循環操作，直到取到的數據在范圍圈內為止。

第二步：數據確定在范圍圈內，另一個問題是數據具體是在六個電壓值中的哪一個，檢測到的數據值，可能在它們之間，而且任何檢測都不可能完全匹配，數據存在誤差范圍，誤差范圍是電壓值的百分之五左右，本算法，限定的百分比是百分之十，之所以限定在百分之十，是因為檢測的數據可能比標準的數值差一部分。公式為：

其中，UF為設置的最大范圍。若有個別數據不在范圍圈內，回到第一步，重新計算。

第三步：在計算好標準的數據后，先將相應的公共電壓值設置好，根據設置好的電壓計算電壓偏差，電壓偏差計算公式為：

其中，UC為檢測到具體數值，UN為公用電壓諧波電壓數值表中的電壓值其中之一。

第四步：電壓檢測時，可能有非線性用電設備在長時間工作，使得無法測得內部數據，于是在第一步的基礎上，電壓偏差還需再擴大百分之五，計算公式為：

其中，ΔU1表示多值波動范圍。

第五步：計算出電壓范圍差值之后，再計算相應的上限電壓和下限電壓，上限電壓為：

其中，U上表示最大上限范圍。

下限電壓為：

其中，U下表示最小下限范圍。

第六步：計算出上、下限最大范圍，超出這個范圍就為無用電壓數據，在這個范圍內才可以成為有用數據，如果有一段數據都超出這個范圍，對此只能強制的變換成為標準數據，預留存儲區存放的數據具體公式為：

第七步：設置好電壓后，按照改進極值中值濾波算法的原理再次過濾數據，這樣，最后保留下來的數據基本都是在標準范圍之間的數據。這樣不論數據在一段范圍內是否受到污染，都可以用改進的算法存儲數據。

3 數據結果對比

下面簡述傳統的算法與新式算法的數據對比，以標準電壓是6KV 為例，采集到了100 數據點，傳統的中值過濾算法刪除的數據如表2所示。

表2 極值中值濾波電壓數值表

刪除不合格的灰色數據后，形成的新的數據并經分組后的到的新數據如表3所示。

表3 極值中值濾波電壓數值排序表

表3中間加粗部分是極值中值算法得出的中值數據，灰色部分的三個數據是波動較大的數據。如果應用改進的極值中值濾波算法，這三個波動性較大的數據會被有效刪除，首先就是組成坐標為：(6.02,6.13)，(5.39,5.60)，(6.32,5.41)，(6.23,6.01)，(6.00,5.41)，…，但是像采集數據的最后一組數據(5.79,10.98)，會被此算法排除。其他的這些坐標全部在范圍圈內，可以確定此電壓的標準值為6KV，接下來是對數據分析。

從表3、表4 可以看出，表4 多刪除了三個波動性更大的數據，形成的新的數據并經分組后的到的數據如表5所示。

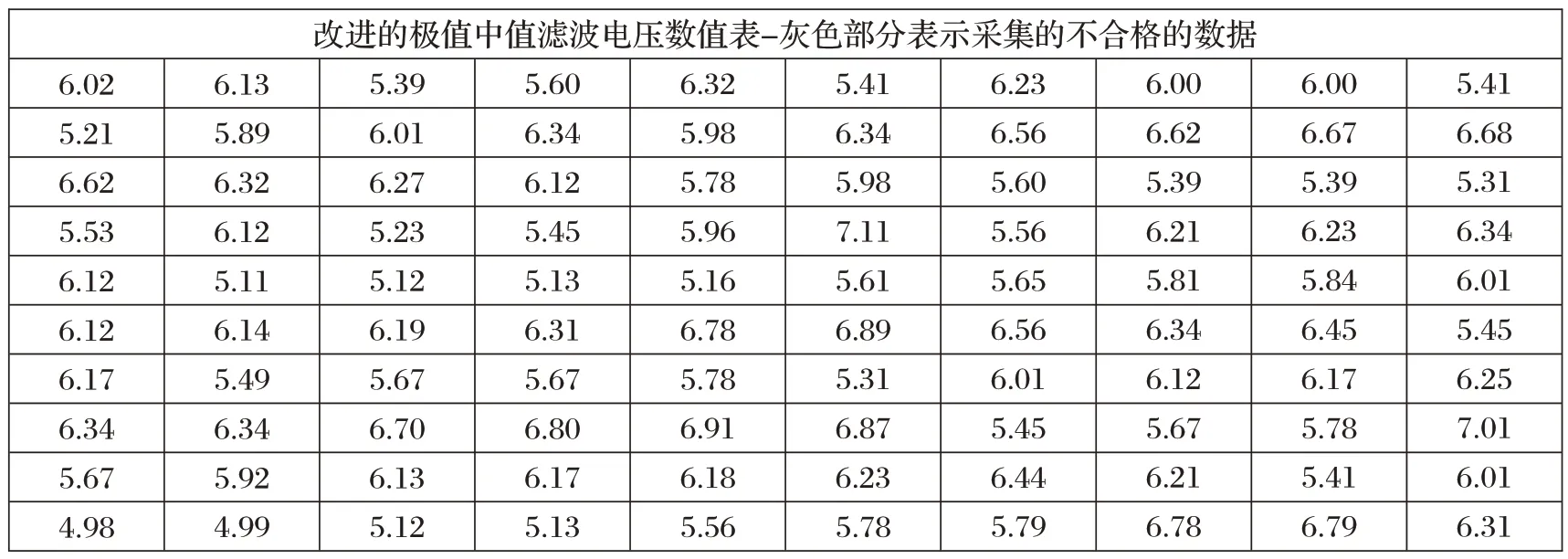
表4 改進的極值中值濾波電壓數值表

表5 改進的極值中值濾波電壓數值排序表

可以看到，改進的極值中值濾波算法比極值中值濾波算法過濾的更好一些，極值中值與改進的算法的數據對比如圖2 所示。極值中值濾波算法方差波動大，改進的算法相對波動的就小。

圖2 極值中值與改進的算法的數據對比

4 結論

利用中值原理，對當前的極值中路濾波算法進行改進，對收集好的數據進行濾波，將波動性大的數據刪除，保留下波動性相對較小、滿足算法理論條件的數據，提高了電壓檢測數據值的準確率和穩定性。