基于改進卡爾曼濾波的叉車載重快速準確估計方法

黃澤雄 劉 蘭 黃運保 李海艷 黃東華

1.廣東工業(yè)大學機電工程學院，廣州，510006 2.廣東技術師范大學網絡空間安全學院，廣州，510655

0 引言

在生產貿易活動中，對貨物進行搬運和計重是貨物估價必不可缺的環(huán)節(jié)。伸縮臂叉車作為貨物搬運作業(yè)最為有效的工程機械之一，不但具備平衡重式叉車搬運貨物的功能，而且在車身不動的情況下，可以通過伸縮臂伸縮和臂架變幅等操作進行不同高度與距離下的裝卸作業(yè)，從而被廣泛應用于農業(yè)、建筑業(yè)和港口裝卸等領域[1-2]。而現(xiàn)有伸縮臂叉車主要通過轉運過秤的開環(huán)反饋方式[3]對所裝卸的貨物進行估計，效率低下，且需要花費大量的人力物力。

在工程機械載重估計研究領域，目前國內外相關研究主要集中在挖掘機、門座起重機和吊車等工程機械，而對伸縮臂叉車載重估計方面的相關研究目前還未見報道。在國外，MINTAH等[4]于2012年提出了一套液壓挖掘機自適應載重監(jiān)控方案，該方案雖然能夠實現(xiàn)載重自適應估計，但由于有效測量范圍劃分比較難控制，在實際應用中會受到限制。WALAWALKAR等[5]于2016年提出了一種基于測量方式的挖掘機載重估計方法，但是該種方法需要了解工作附件的慣性參數(shù)，并且其數(shù)學模型的求解較為復雜。為此，WALAWALKAR等[6]于2018年通過估計工作附件的質量、質心和質量慣性矩等參數(shù)對載重估計方法進行了改善，但是該方法對關節(jié)角加速度和動臂慣性參數(shù)的計算要求很高。PALOMBA等[7]于2019年提出了一種基于狀態(tài)估計的載重估計方法，該方法是基于挖掘機運動學和動態(tài)模型的兩階段方法進行估計的，從而需要較多種類的傳感器。在國內，溫建明[8]于2008年提出了一套基于模糊神經網絡的門座起重機載重動態(tài)估計方案，但該方案是在假設門座起重機勻速提升貨物的理想化狀態(tài)下進行估計的，且該系統(tǒng)的載重估計誤差達到了5%。李婷婷[9]于2017年提出了一種考慮載重重心偏移和考慮地面坡度的叉裝車自動載重估計算法，該算法能夠有效消除動臂舉升速度、載重重心偏移和地面坡度對載重估計結果的影響。但該算法僅適用于典型的反轉六連桿機構，對于不同的叉裝車工作裝置結構，需要對載重估計數(shù)學模型進行較大的改動。何經旺[10]于2015年結合挖掘機的結構特點和工作環(huán)境的特殊性，根據(jù)Kane動力學理論的動力學和運動學，建立了液壓挖掘機的載重估計數(shù)學模型，然后使用遞推最小二乘算法進行載重動態(tài)估計。該方法可以在液壓挖掘機的任何姿態(tài)下估計出鏟斗載重大小，但因為其數(shù)學模型需要辨識轉動慣量等變量，而轉動慣量的辨識又會涉及到挖掘機各個桿件的實時重心位置，所以在實際作業(yè)中很難進行動態(tài)準確估計。

國內配備有載重估計技術的工程機械的估計系統(tǒng)在準確度和穩(wěn)定性控制等方面都與國外產品有較大的差距，雖然已經研發(fā)了一些估計模型，但計算過于復雜且硬件成本昂貴，目前還沒有一個可靠且有效的載重動態(tài)估計模型。研究一套伸縮臂叉車載重估計方案對國內工程機械智能制造和實現(xiàn)碳達峰、碳中和目標，以及智能化和無人化的貨物搬運場景都具有重大的意義。

本文根據(jù)伸縮臂叉車工作裝置的工作原理和臂架結構的組成特點，對臂架進行動力學分析，建立載重與液壓系統(tǒng)壓力、臂架變幅角度以及伸縮臂伸縮長度之間成線性關系的載重估計數(shù)學模型，然后使用具有實時辨識遞推特點的卡爾曼濾波算法[11]對該模型進行求解。最后，針對卡爾曼濾波算法在遞推過程中載重發(fā)生改變時新測量數(shù)據(jù)對載重估值失去校正能力的缺點，本文提出了一種基于改進卡爾曼濾波的載重估計算法。目前該載重動態(tài)估計方法已初步應用到某企業(yè)的超長重載伸縮臂叉車。

1 載重估計方案分析

本文研究了超長重載伸縮臂叉車，實車如圖1所示，其尺寸和性能參數(shù)如表1所示。

圖1 超長重載伸縮臂叉車Fig.1 Super long and heavy load telescopic handler

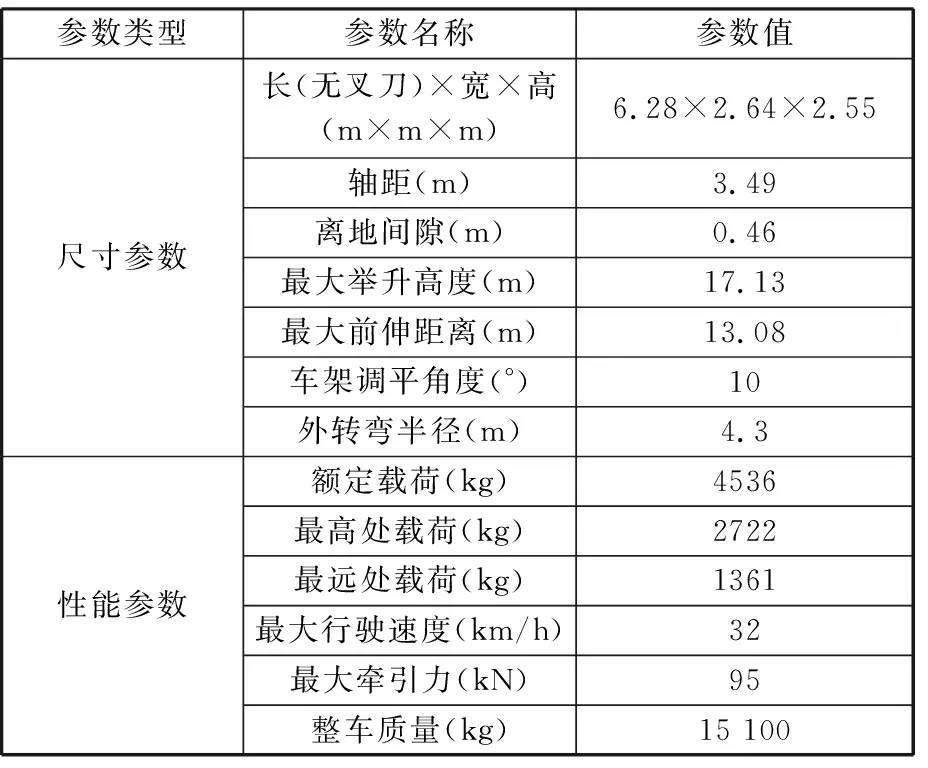
表1 伸縮臂叉車的尺寸和性能參數(shù)

1.1 基于動力學轉動定律間接估計

根據(jù)一些已有的工程機械工作載荷估計方案，結合伸縮臂叉車的工作原理，提出了如下三種工作載荷估計方案：

(1)采用機械軸式傳感器直接估計，在伸縮臂叉車第四級臂與貨叉的支撐鉸鏈處安裝壓力傳感器，然后在某個固定姿態(tài)下，通過對測得的傳感器信號進行運算處理，直接對載重進行估計；

(2)基于靜力學力矩平衡原理[12]間接估計，將臂架固定在某個確定的變幅角度，用位移傳感器和壓力傳感器分別靜止采集伸縮臂伸縮長度、變幅液壓缸和隨動液壓缸有/無桿腔壓力，利用靜力學力矩平衡原理建立載重估計數(shù)學模型，間接對載重進行估計[13]；

(3)基于動力學轉動定律[14]間接估計，與第二個方案不同，該方案是在作業(yè)過程中動態(tài)采集臂架變幅角度、伸縮臂伸縮長度、變幅液壓缸和隨動液壓缸有/無桿腔壓力，然后根據(jù)動力學轉動定律建立的函數(shù)關系式，實現(xiàn)動態(tài)載重估計。

對各方案進行比較分析：方案(1)雖然以直接測量的方式能夠實現(xiàn)載重動態(tài)估計，且估計準確度高、成本低。但是在作業(yè)環(huán)境惡劣、叉具頻繁更換，以及軸銷旋轉時壓力傳感器會受旋轉力作用的情況下，容易導致壓力傳感器失效和損耗，在實際應用中會存在故障率高、使用壽命短和局限性大等問題[15]；方案(2)理論上能達到較高的稱重精度，但需要靜態(tài)測量，作業(yè)效率較低；方案(3)所建立的載重估計數(shù)學模型具有較強的實用性和較高的估計準確度，被目前工程機械載重估計領域應用得最為廣泛[16-17]。

綜合比較以上三個載重估計方案的優(yōu)缺點，最終確定采用第三個方案，在不額外增加其他類型傳感器的情況下，利用叉車工作裝置現(xiàn)有功能模塊中已裝配的角度傳感器、位移傳感器和壓力傳感器實現(xiàn)叉車載重動態(tài)估計。

1.2 建立載重估計數(shù)學模型

為了簡化力學分析和幾何分析，假設臂架中心面與底盤縱向中垂面重合，將組成臂架的所有構件都置于這一平面坐標系內，以臂架與車架的回轉銷軸鉸接點O為坐標原點，沿伸縮臂叉車行駛的水平方向為X軸正向，垂直于X軸的豎直向上方向為Z軸正向。將伸縮臂處于全縮回且處于水平狀態(tài)的位置設為臂架的初始位置。假設各構件均為均質材料，其幾何中心即重心，則構件的重心相對于X軸正向的變幅角度定義為Δθ，除此之外，還假設重心只沿變幅角度Δθ的射線上偏移。伸縮臂叉車的載重估計力學模型簡圖見圖2，其中，O為臂架與車架的鉸接點；J為變幅液壓缸缸桿與基本臂的鉸接點；S為變幅液壓缸缸筒與車架的鉸接點；M為隨動液壓缸缸桿與基本臂的鉸接點；N為隨動液壓缸缸筒與車架的鉸接點；F為四級臂頭部與貨叉的鉸接點。

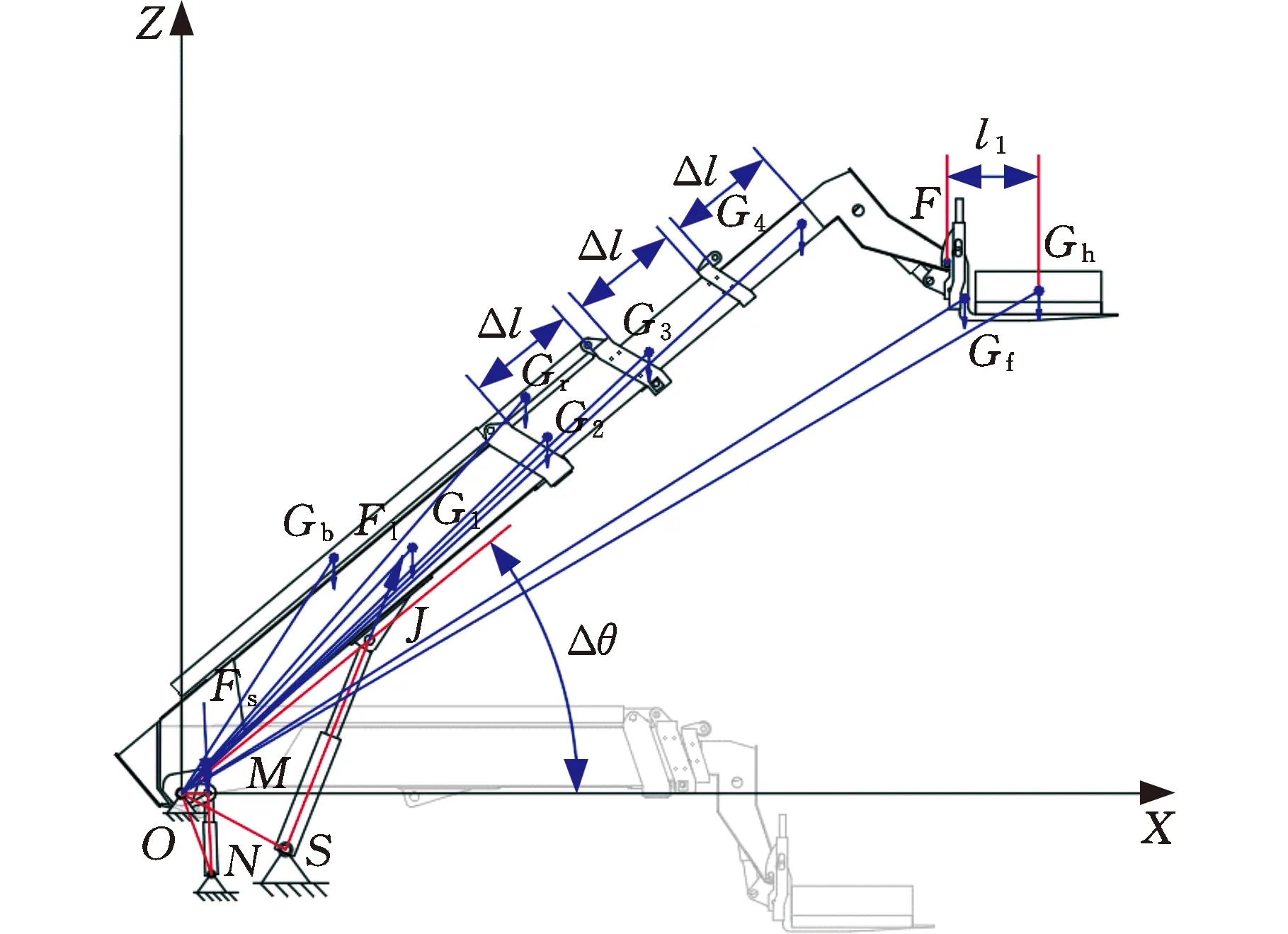
圖2 伸縮臂叉車的載重估計力學模型簡圖Fig.2 Mechanical model diagram for load estimationof telescopic handler

在計算臂架自重對轉動軸的力矩時，若直接將四個節(jié)臂、伸縮液壓缸、調平液壓缸、搖桿、連桿、貨叉和連接件作為一個整體分析，當叉車進行變幅和伸縮等操作時，其整體重心位置就會難以確定。所以，這里采用離散化的思想，將臂架分成幾個主要構件，然后逐個分析臂架伸縮變幅時各主要構件重心的運動規(guī)律。

由于叉車工作裝置部分在正常工作時，基本臂是通過一根水平銷軸與車架松連接的，故臂架受到車架對其支承力的作用可以忽略不計，而摩擦力和調平液壓缸對貨叉的推力作為臂架的內力則不計算在內。臂架在車身縱截面XOZ內會受到變幅液壓缸的作用力Fl、隨動液壓缸的作用力Fs、載重重力Gh和臂架中各主要構件的自身重力。由于伸縮臂叉車在起吊的時候必須打開支腿且不能移動，因此伸縮臂只能在變幅角度內運動，水平慣性力幾乎沒有。再進一步忽略慣性較小的調平液壓缸等構件對臂架動力學性能的影響后，伸縮臂叉車臂架繞定軸轉動的微分方程為

JMα=FlLl+FsLs-G1L1-G2L2-
G3L3-G4L4-GbLb-GrLr-GfLf-GhLh

(1)

式中，JM為臂架對轉動軸的轉動慣量；α為臂架的角加速度，即對臂架變幅角度Δθ求時間的二階導數(shù)；G1、G2、G3、G4、Gb、Gr、Gf、Gh分別為基本臂、二級臂、三級臂、四級臂、伸縮液壓缸缸筒、伸縮液壓缸缸桿、貨叉以及載重的重力；L1、L2、L3、L4、Lb、Lr、Lf、Lh分別為相對應構件重力對轉動軸的力臂；Fl、Fs分別為變幅液壓缸和隨動液壓缸對臂架的作用力；Ll、Ls分別為變幅液壓缸和隨動液壓缸作用力對轉動軸的力臂。

對式(1)進一步分析，在合外力矩給定的情況下，剛體的轉動慣量越大，則所獲得的角加速度越小，即角速度改變得慢，剛體保持原有轉動狀態(tài)的慣性就越大。考慮臂架在變幅伸縮動作的起始加速和終止減速階段，其角加速度α較大，會對載重估計有影響，但伸縮臂叉車臂架的轉動慣量也大，且在變幅伸縮過程中大部分時間內都是處于穩(wěn)定階段的。所以一般認為臂架在貨物變幅升降過程中其角速度是不變的，或者說角加速度幾乎為零。這時，則可以忽略角加速度α的影響，從而避免臂架中各構件因質量和重心位置的不準確而造成動力學中關于轉動慣量的復雜計算[18]。故有合外力矩∑MT=0，則式(1)等價于：

G1L1+G2L2+G3L3+G4L4+GbLb+GrLr+
GfLf+GhLh=FlLl+FsLs

(2)

如圖3所示，計算變幅液壓缸推力對轉動軸的力臂。先根據(jù)余弦定理，計算出變幅液壓缸上鉸接點J到變幅液壓缸下鉸接點S的距離lJS，然后用面積公式計算三角形ΔJOS的面積，最后根據(jù)同一三角形面積相等，即可計算變幅液壓缸推力對轉動軸的力臂Ll，其表達式為

(3)

θl=θOJ+|θOS|

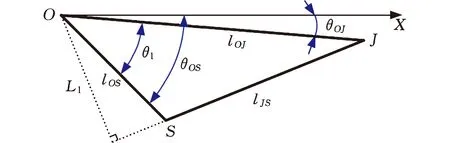
圖3 變幅液壓缸對轉動軸的力臂Fig.3 Luffing hydraulic cylinder to the rotatingshaft force arm

式中，lOJ為臂架處于水平狀態(tài)時，變幅液壓缸上鉸接點J到轉動點O的距離；lOS為變幅液壓缸下鉸接點S到轉動點O的距離；lJS為臂架處于水平狀態(tài)時，變幅液壓缸上鉸接點J到變幅液壓缸下鉸接點S的距離；θl為臂架處于水平狀態(tài)時，變幅液壓缸上鉸接點J、下鉸接點S與轉動點O形成∠JOS的角度；θOJ為臂架處于水平狀態(tài)時，lOJ與X軸之間的初始角度；θOS為lOS與X軸之間的角度。

隨動液壓缸阻尼力對轉動軸的力臂Ls也可根據(jù)式(3)同理計算得到。根據(jù)各臂架中各主要構件的幾何結構及其重心位置的平面坐標關系，將求解得到的有關量代入式(2)，再對該式的左邊分離出變量臂架變幅角度Δθ和伸縮臂伸縮長度Δl可得到以下關系式：

a1cosΔθ-a2sinΔθ+a3ΔLcosΔθ+a4=

(4)

式中,a1、a2、a3、a4為未知參數(shù)；lOM為臂架處于水平狀態(tài)時，隨動液壓缸上鉸接點M到轉動點O的距離；lON為隨動液壓缸下鉸接點N到轉動點O的距離；lMN為臂架處于水平狀態(tài)時，隨動液壓缸上鉸接點M到隨動液壓缸下鉸接點N的距離；θs為臂架處于水平狀態(tài)時，隨動液壓缸上鉸接點M、下鉸接點N與轉動點O形成∠MON的角度。

進一步將式(4)化簡成矩陣的形式：

Φ·Θ=MT

(5)

Φ=[a1a2a3a4]

Θ=[cosθ-sinθΔlcosθ1]T

式中,MT為變幅液壓缸壓力和隨動液壓缸壓力對臂架的合外力矩。

根據(jù)式(4)，在伸縮臂叉車處于空載的情況下，即Gh=0時，采集數(shù)學模型所需的全部可測變量：臂架變幅角度Δθ，伸縮臂伸縮長度Δl，以及變幅液壓缸和隨動液壓缸有/無桿腔的壓力plb、plr、psb、psr，然后將信號數(shù)據(jù)截取有效區(qū)間部分，即可辨識出四個未知參數(shù)：a1、a2、a3、a4。

將計算得到的載重重力對轉動軸的力臂代入式(5)，即可求得出載重重力Gh與臂架變幅角度Δθ、伸縮臂伸縮長度Δl，以及變幅液壓缸和隨動液壓缸有/無桿腔的壓力plb、plr、psb、psr之間的函數(shù)關系，即載重計算公式為

LhGh=MT-Φ·Θ

(6)

2 基于改進卡爾曼濾波的載重估計數(shù)學模型求解算法

參數(shù)估計法[19]可以將載重估計作為一個參數(shù)估計和預測問題進行辨識遞推，本質上可以看作是載重估計模型辨識及其參數(shù)估計問題：將載重估計過程作為一個參數(shù)辯識的問題來處理，根據(jù)已經建立好的載重估計數(shù)學模型，推導出一個含有未知參數(shù)的模型，然后用該模型去擬合載重估計過程的輸出信號，從而獲得最小均方誤差意義上的參數(shù)估計[20]。

卡爾曼濾波算法屬于模型辨識與參數(shù)估計方法中的一種，該算法采用辨識遞推的方式，只需在上一次結果的基礎上進行下一步的運算，不需要將數(shù)據(jù)進行儲存，且運算量小，適用于實時過程，可以用來估計只能被系統(tǒng)本身間接或不精確測量的狀態(tài)變量。

卡爾曼濾波算法的方程分為兩組：預測更新方程和測量更新方程[21-23]。在預測更新階段，利用前一時刻的狀態(tài)估計值對當前時刻狀態(tài)進行估計；而在測量更新階段，則利用當前時刻狀態(tài)的測量值修正預測更新階段的預測值，以獲得一個更為精確的當前時刻狀態(tài)估計。

將載重重力Gh作為該載重估計系統(tǒng)t時刻的狀態(tài)變量；在該估計過程中默認前后兩個時刻的載重不發(fā)生改變，即相鄰兩個時刻的狀態(tài)并無切換，所以將狀態(tài)轉換參數(shù)A設置為1；由于系統(tǒng)中無控制信號輸入，故將控制信號U(t)設置為0，控制狀態(tài)參數(shù)B也設置為0。則預測更新方程可表示為

(7)

在預測更新階段，還需要計算t時刻的先驗估計誤差協(xié)方差P-(t)：

P-(t)=P(t-1)+Q

(8)

式中，P(t-1)為t-1時刻的后驗估計誤差協(xié)方差；Q為過程誤差W(t)的協(xié)方差。

將載重計算公式作為估計過程的測量更新方程：

Z(t)=Lh(t)Gh(t)+V(t)=MT(t)-
Φ·Θ(t)+V(t)

(9)

Θ(t)=[cos(θ(t)) -sin(θ(t)) Δl(t)cos(θ(t)) 1]T

式中,V(t)為測量誤差。

在測量更新階段，首先需要根據(jù)預測更新部分得到的t時刻先驗估計誤差協(xié)方差P-(t)和測量誤差V(t)的協(xié)方差R計算出t時刻的卡爾曼增益K(t)：

(10)

(11)

最后，還需要根據(jù)t時刻的先驗估計誤差協(xié)方差P-(t)和卡爾曼增益K(t)得到t時刻的后驗估計誤差協(xié)方差P(t)：

P(t)=(1-K(t)Lh(t))P-(t)

(12)

基于卡爾曼濾波的載重估計算法流程如圖4所示,可以看出，隨著辨識遞推的進行，當后驗估計誤差協(xié)方差P(t)減小至0時，載重估計過程將停止。

圖4 基于卡爾曼濾波的載重估計算法流程Fig.4 Algorithm flow of workload estimation based onKalman filter

在卡爾曼濾波算法辨識遞推的過程中，由于后驗估計誤差協(xié)方差P(t)和卡爾曼增益K(t)會迅速衰減到0，并使得大量新測量數(shù)據(jù)失去對狀態(tài)變量的校正能力，這種現(xiàn)象稱為數(shù)據(jù)飽和。因此需考慮校正方案，以保持新測量數(shù)據(jù)對狀態(tài)變量估計的持續(xù)校正能力，進而使載重估計系統(tǒng)能得到準確的估計值。如圖5所示的一組數(shù)據(jù)，在t=100 s時，載重已經發(fā)生了很大的改變，但隨著P(t)和K(t)快速減小到0，其估計值mh并不能很好地從1500 kg附近迅速地遞推到1000 kg附近。

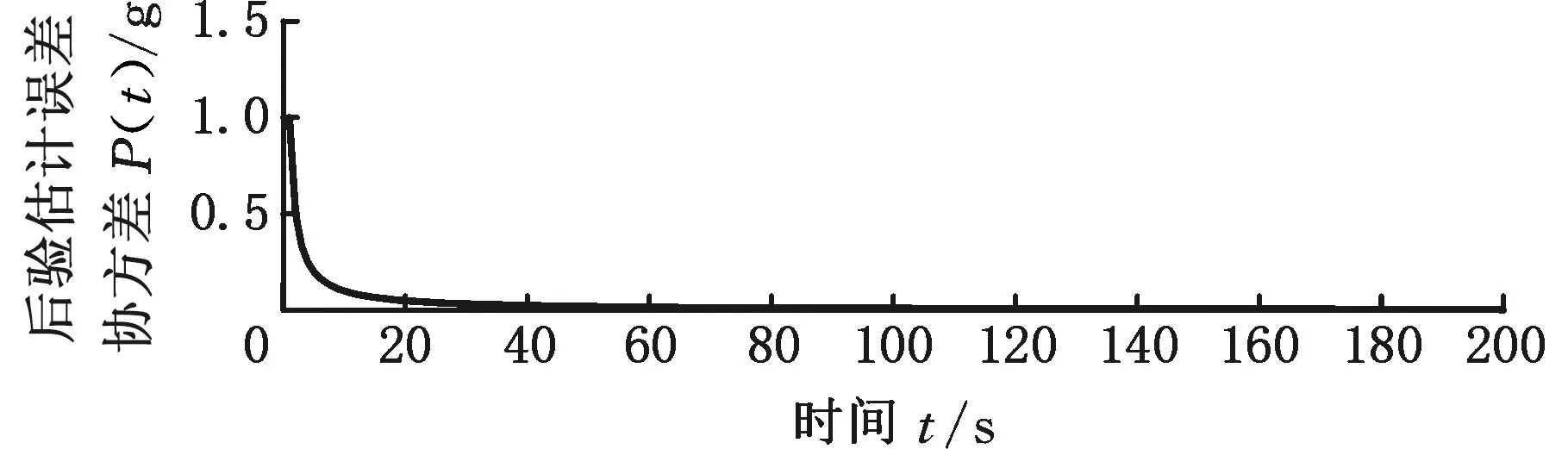
(a)載重質量的后驗估計誤差協(xié)方差

對該現(xiàn)象進一步分析可知，當載重發(fā)生改變時，即該估計過程的狀態(tài)變量已發(fā)生了變化,此時的估計過程與狀態(tài)變量改變前的估計過程已經不是同一過程了，而且此時的后驗估計誤差協(xié)方差也已減小到0，若再延續(xù)前一估計過程繼續(xù)估計，則卡爾曼濾波算法將會無法繼續(xù)準確遞推。

本文受到交互式多模型(interacting multiple model，IMM)[24]的啟發(fā)，采用兩個并行計算的卡爾曼濾波對載重估計數(shù)學模型進行辨識遞推：第一個卡爾曼濾波主要是起到自適應判斷載重是否有較大幅度變化的作用，通過實時監(jiān)控前后兩時刻狀態(tài)變量之差的更新率，為其設置合適的閾值，進而決定是否重置第二個卡爾曼濾波的后驗估計誤差協(xié)方差，以達到快速響應的效果；第二個卡爾曼濾波主要是起到穩(wěn)定估計值的效果，其狀態(tài)變量作為全過程載重估計值的輸出。

基于改進卡爾曼濾波的載重估計算法流程如圖6所示，具體過程如下。

圖6 基于改進卡爾曼濾波的載重估計算法流程Fig.6 Workflow of workload estimation algorithmbased on improved Kalman filter

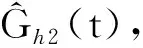
后驗估計誤差協(xié)方差P1(t)和P2(t)重置為初始值的目的是，使大量新測量數(shù)據(jù)保持對載重估計的校正能力；而采用兩個并行計算的卡爾曼濾波進行遞推的方式能夠起到自適應估計的作用，快速辨識出載重發(fā)生變化的時間點，并準確估計出變化前后的載重。

3 載重估計試驗驗證

3.1 試驗平臺搭建

試驗平臺以某企業(yè)研發(fā)的超長重載伸縮臂叉車為研究對象，具體的基礎配置、尺寸參數(shù)和性能參數(shù)已在前文給出。為了減小各類型傳感器測量誤差對載重估計準確度的影響，保證其采集信號數(shù)據(jù)的測量精度，試驗采用的傳感器包括：Gefran公司GSF系列的位移傳感器，長沙灣流智能科技有限公司的VALUER SpaceVector高動態(tài)空間角度傳感器，Danfoss公司MBS3000型號的壓力傳感器。傳感器的安裝位置如圖7所示。

(a)角度傳感器 (b)位移傳感器 (c)隨動液壓缸 (d)變幅液壓缸圖7 傳感器的安裝位置Fig.7 Installation position of sensor

如圖7a中白實線圈所示，在第四級臂的頭部安裝高性能角度傳感器，用于實時測量臂架變幅角度。如圖7b中白實線圈所示，在基本臂安裝拉繩式位移傳感器，導線掛在第二級臂，當伸縮臂進行伸縮動作時，實時測量伸縮臂伸縮長度。圖7c所示為隨動液壓缸；圖7d所示為變幅液壓缸，其中白實線圈內為變幅液壓缸無桿腔壓力測點，白虛線圈內為變幅液壓缸有桿腔壓力測點，在測點處安裝壓力傳感器，則可以測量變幅液壓缸四個腔的壓力。

圖8 電氣系統(tǒng)的主要控制架構Fig.8 Main control architecture of electrical system

伸縮臂叉車電氣系統(tǒng)的主要控制架構如圖8所示。可以看出，位移傳感器和角度傳感器以及與采集電路板檢測裝置的壓力信號輸入端連接的四個壓力傳感器通過CAN總線將這六個傳感器的模擬量數(shù)據(jù)發(fā)送到主控制器；然后，由主控制器讀取傳感器輸出得模擬量數(shù)據(jù)并轉換成數(shù)字量，再將其發(fā)送到CAN總線；最后，由主控制器中的載重估計算法模塊進行運算處理，最后再將估計結果發(fā)送到CAN總線，且由顯示器接收并顯示。

在試驗平臺的搭建過程中，為了能夠充分滿足應變、位移和壓力等不同類型信號數(shù)據(jù)的輸入要求，這里使用HBM公司的SoMat eDAQ數(shù)據(jù)采集系統(tǒng)進行數(shù)據(jù)采集與分析。將壓力傳感器連接到臂架系統(tǒng)的液壓油路，從總線中接出電信號的采集數(shù)據(jù)，將壓力傳感器輸出線接入與計算機直接連接的數(shù)據(jù)采集儀，即可將信號數(shù)據(jù)輸出至計算機中，然后使用SoMat TCE軟件進行信號數(shù)據(jù)采集，試驗時的采集頻率設置為40 Hz。數(shù)據(jù)采集儀與計算機直接連接如圖9所示。

圖9 Somat eDAQ數(shù)據(jù)采集儀與計算機直接連接Fig.9 Somat EDAQ data acquisition instrument isdirectly connected with the computer

3.2 算法初值選擇和參數(shù)設置

算法中參數(shù)的說明與設置如下：

(2)后驗估計誤差協(xié)方差初始值。由式(10)可知，在測量誤差協(xié)方差R確定的情況下，卡爾曼增益K(t)與先驗估計誤差協(xié)方差P-(t)正相關；而由式(8)可知，在過程誤差協(xié)方差Q確定的情況下，P-(t)又與后驗估計誤差協(xié)方差P(t)成正比的關系。故P(t)的初值越大，就會使遞推過程中計算的K(t)就越大，則意味著實際測量值Z(t)更可信。在該載重估計系統(tǒng)中，由于液壓系統(tǒng)壓力的測量噪聲是很大的，故后驗估計誤差協(xié)方差的初始值P1(0)、P2(0)都設置為100。

(3)測量誤差協(xié)方差初始值。由預測更新方程和測量更新方程可知，載重估計系統(tǒng)某一時刻的載重值會有兩個，分別為經驗的預測值和模型的測量值，而卡爾曼濾波算法需要在預測值和測量值之間的過渡階段，結合過程噪聲W(t)和測量誤差V(t)，遞推出該系統(tǒng)在統(tǒng)計意義下最為接近載重真實值的最優(yōu)估計值，因此在遞推過程中到達穩(wěn)定估計值之前會具有一個過渡階段。而測量誤差協(xié)方差R則會影響該過渡階段所需要的時間以及載重估計值與真實值之間的近似程度。當R比較小時，意味著實際測量值Z(t)越來越可信，而估計測量值Lh(t)Gh(t)則越來越不可信，此時算法收斂至穩(wěn)定估計值的響應時間很短，但當R過小時，系統(tǒng)容易出現(xiàn)震蕩現(xiàn)象；當R比較大時，意味著Z(t)的可信度越來越低，而Lh(t)Gh(t)則越來越可信，此時算法收斂速度很慢，系統(tǒng)的響應時間較長[25]。在實際應用中，可以采集一些離線樣本信號，并對其測量信號的噪聲，通過分析純噪聲來對R進行確定。通過多次試驗的參數(shù)調整，卡爾曼濾波Γ1和Γ2的R取0.01～1.00。

(4)過程誤差協(xié)方差初始值。過程誤差協(xié)方差Q表示建立的預測模型本身帶來的噪聲，該參數(shù)被用來表示狀態(tài)轉換參數(shù)A與實際過程之間的誤差。Q會影響辨識遞推后曲線的平滑程度，因為無法直接觀察系統(tǒng)的估計過程，所以確定其大小是比較困難的。由于在該載重估計過程中默認前后兩個時刻的載重是不發(fā)生改變的，故卡爾曼濾波Γ1和Γ2的Q都取0[26]。

(5)若卡爾曼濾波Γ1中的閾值γ過小，則會影響系統(tǒng)估計值的不穩(wěn)定性；若γ過大，則會延長估計系統(tǒng)的響應時間。故γ一般取一到兩個采樣周期，這里取40～80個采樣點。閾值β表示為判斷載重發(fā)生變化的幅度，變化幅度一旦超過閾值就會觸發(fā)后驗估計誤差協(xié)方差P2(t)重置為初始值，這時估計過程將重新開始。閾值β根據(jù)試驗時的經驗值，取200～500 kg。

3.3 離線試驗結果與分析

進行了四組不同載重的離線試驗，驗證所提出的基于改進卡爾曼濾波的載重估計算法是否達到以下產品研發(fā)要求：

(1)對于454 kg的輕載荷，其估計結果的最大絕對誤差應小于91 kg。因為該載重估計數(shù)學模型主要利用液壓系統(tǒng)壓力信號實現(xiàn)間接估計，輕載對液壓缸壓力變化的敏感度較小，伸縮臂叉車臂架的穩(wěn)定性較差，從而會導致估計難度陡增，所以在輕載情況下，估計精度可以適當?shù)亟档汀?/p>

(2)對于2268 kg、3368 kg和4536 kg的重載荷，其估計結果的平均絕對百分比誤差應小于3%。

(3)在臂架變幅和伸縮臂伸縮等多任務況造成較大的沖擊時，算法依然能夠快速收斂到真實值，即算法需要滿足載重估計的穩(wěn)定性。

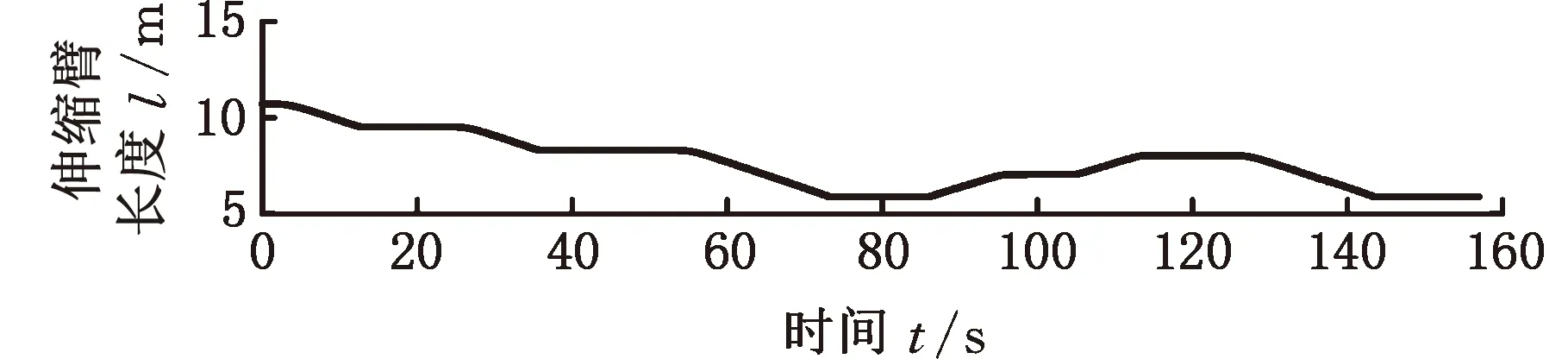
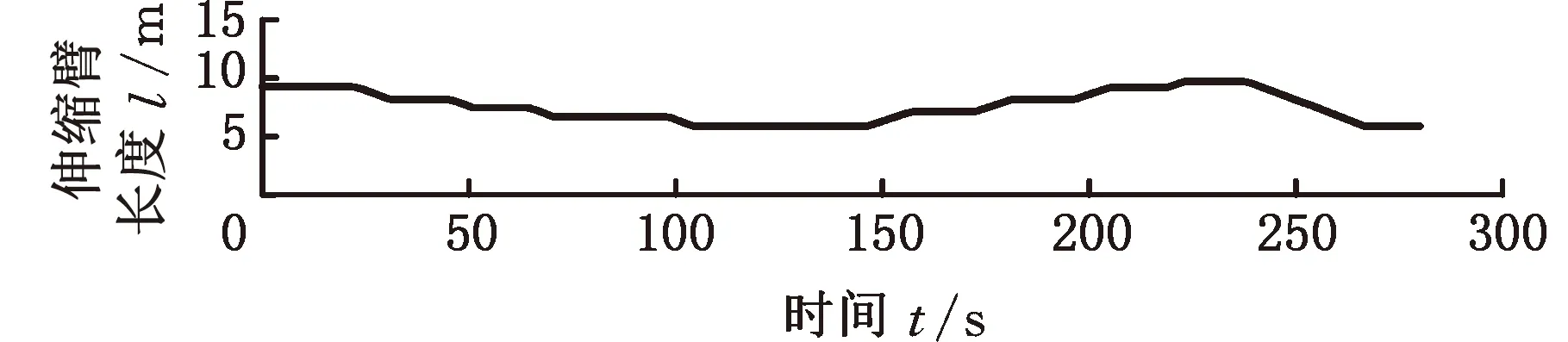
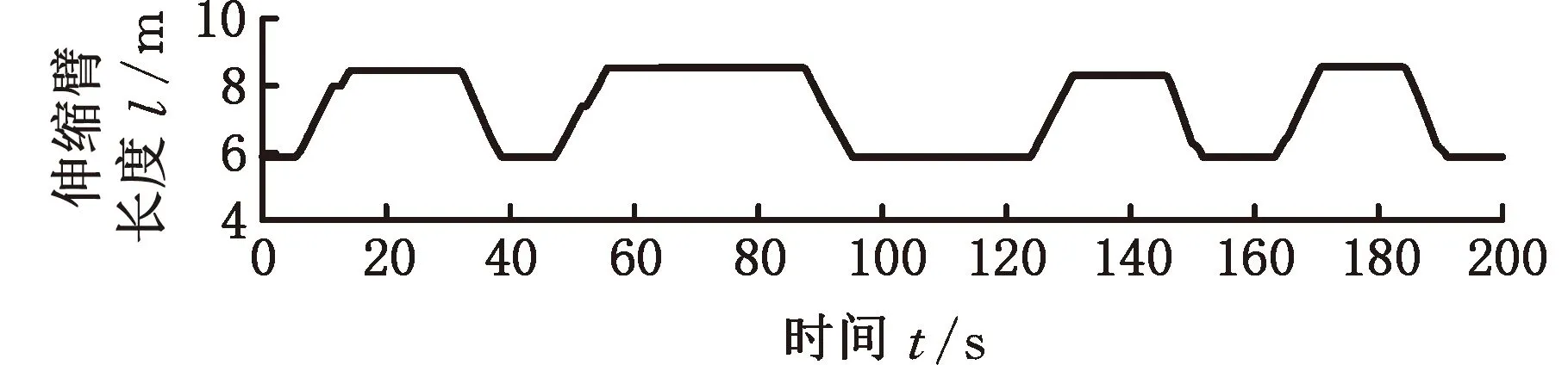
離線試驗的結果如圖10～圖13所示，其中伸縮臂長度l為基本臂與3倍伸縮臂伸縮長度Δl之和。離線試驗是在MATLAB2019a環(huán)境下進行的，計算機處理器為英特爾第三代酷睿i5-3320M 2.60 GHz，運行內存為海力士8GB DDR3L 1600 MHz。

(a)伸縮臂長度

(a)伸縮臂長度

(a)伸縮臂長度

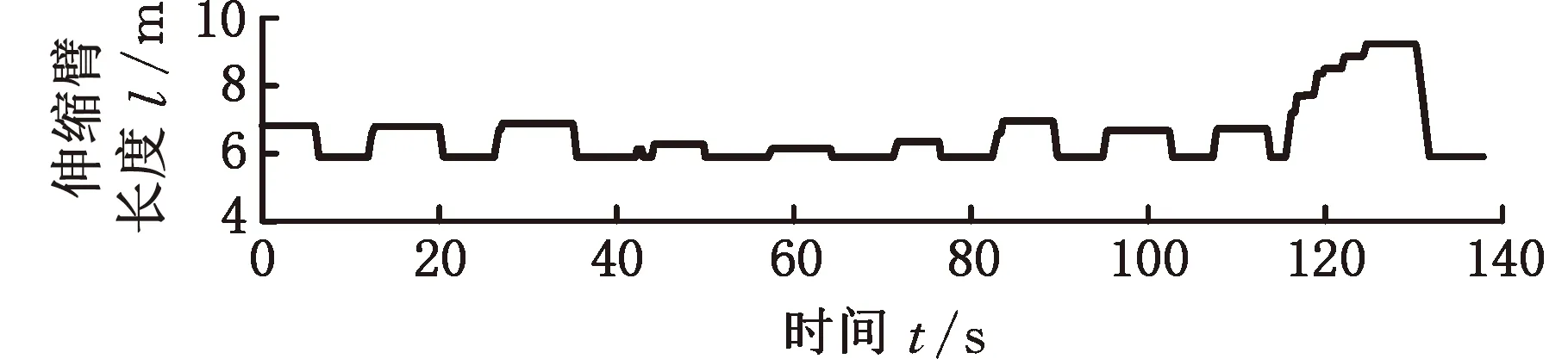
(a)伸縮臂長度

分析圖10～圖13的臂架變幅和伸縮臂伸縮過程可以發(fā)現(xiàn)，當進行變幅和伸縮動作時，會造成液壓系統(tǒng)壓力振蕩等不穩(wěn)定性情況，在未使用載重估計算法辨識遞推而根據(jù)載重計算公式直接求解時，載重會有相當大的波動，嚴重偏離了真實值；而使用載重估計算法辨識遞推之后，載重估計值可以快速收斂至真實值。辨識遞推前后的載重質量見表2。

表2 辨識遞推前后的載重質量(離線試驗)

使用最大絕對百分比誤差emax和平均絕對百分比誤差emape以及其辨識遞推過程所需的計算處理時間對所提出的基于改進卡爾曼濾波的載重估計算法進行定性和定量評價。emape表示估計值較真實值的平均偏離程度，其值越小，說明載重估計模型準確度越高。辨識遞推后的載重絕對百分比誤差及計算時間見表3。

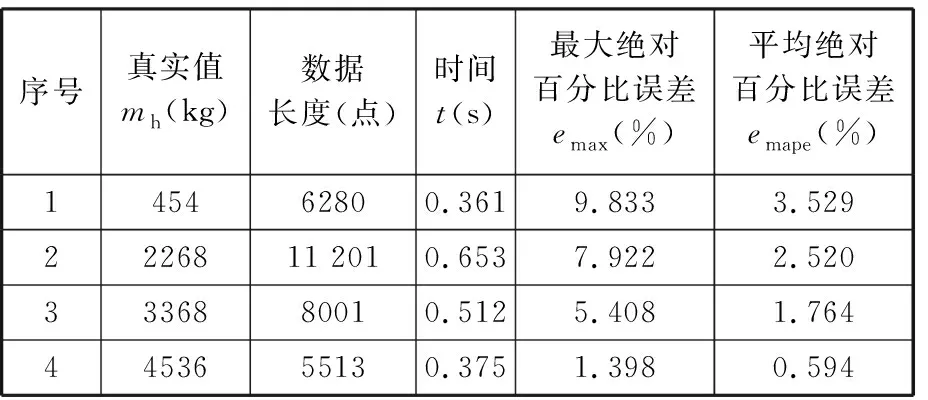
表3 辨識遞推后的載重絕對百分比誤差及計算時間

由表3可以看出，經過載重估計算法快速準確辨識遞推之后，除了第1組454 kg的載重試驗外，第2～4組試驗的平均絕對百分比誤差都在3%以內；再結合圖10～圖13來看，最大絕對百分比誤差都是在臂架變幅上升的初始階段或變幅角度最大的位置(紅實圈處)，因為在這些位置上，伸縮臂處于變幅的極限位置或者叉具觸碰地面等情況，導致整個臂架受力比較復雜；對于454 kg的載重試驗，其平均絕對百分比誤差和最大絕對百分比誤差都比較大，但其最大絕對百分比誤差9.833%在要求的范圍內；從辨識遞推時間來看，基于改進卡爾曼濾波的載重估計算法的計算效率比較高。根據(jù)離線試驗的分析結果，初步達到了試驗的目的與研發(fā)的要求。

3.4 在線試驗結果與分析

最終的在線試驗結果如圖14～圖18所示。對圖14～圖18中伸縮臂叉車帶載重時臂架變幅和伸縮臂伸縮過程分析可知：

(1)對比辨識遞推前后的載重質量，使用基于改進卡爾曼濾波的載重估計算法求解該數(shù)學模型，估計結果的穩(wěn)定性得到了很大改善，即使辨識遞推前載重會有相當大的波動，辨識遞推后也可以快速收斂至載重估計值真實值附近；

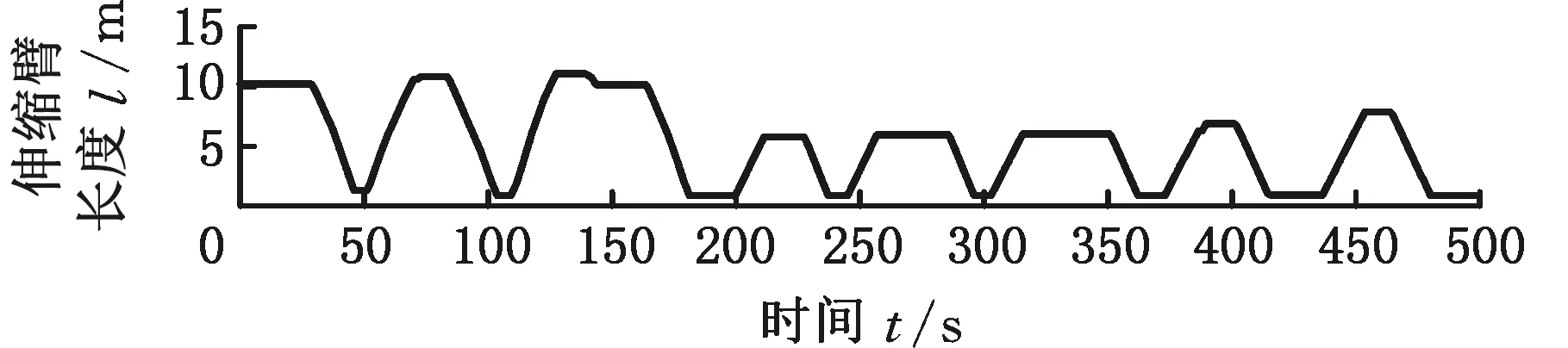
(a)伸縮臂長度

(a)伸縮臂長度

(2)當要叉起一個置于地面的貨物時，由于提升前貨叉是處于松弛狀態(tài)，而伸縮臂叉車以較快的速度突然變幅提升載重，這樣的起升過程會產生一個較大的慣性沖擊，從而導致載重估計值偏離真實值(紅實線圈處)。所以為了提高載重估計的準確度，在作業(yè)現(xiàn)場，操作員應當以較低的速度叉起重物，進而使臂架逐漸受力及變形后，再以額定速度變幅提升；

(3)當臂架變幅角度達到最大角度71°或者變幅角度為0°時，整車的穩(wěn)定性能最差，載重估計值會產生較大的波動(紅虛線圈處)。這是由于液壓系統(tǒng)的泄壓、保壓和漏油等原因造成的。

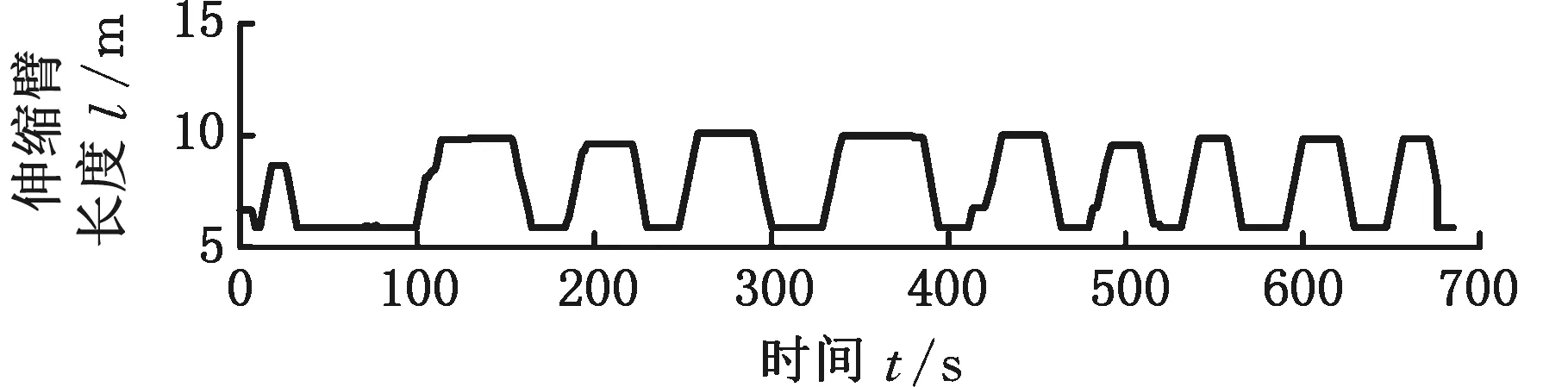
(a)伸縮臂長度

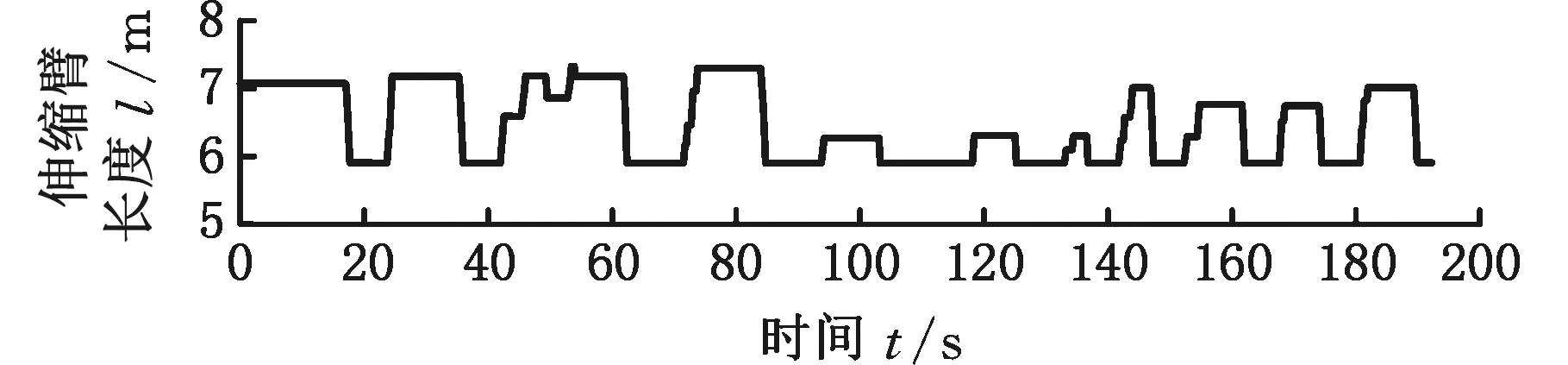
(a)伸縮臂長度

以上5組不同載重的在線試驗，其辨識遞推前后的載重質量見表4。辨識遞推后的載重絕對百分比誤差見表5。

由表5可以看出，經過載重估計算法快速準確辨識遞推之后，除了第5組454 kg的載重試驗外，第6～9組試驗的平均絕對百分比誤差都在3%以內；與離線試驗相同，最大絕對百分比誤差也都是伸縮臂處于變幅范圍的極限位置或在變幅提升的初始階段；對于第5組454 kg的載重試驗，其平均絕對百分比誤差和最大絕對百分比誤差也比較大，其最大絕對百分比誤差16.142%，但也在要求的范圍內。

(a)伸縮臂長度

表4 辨識遞推前后的載重質量(在線試驗)

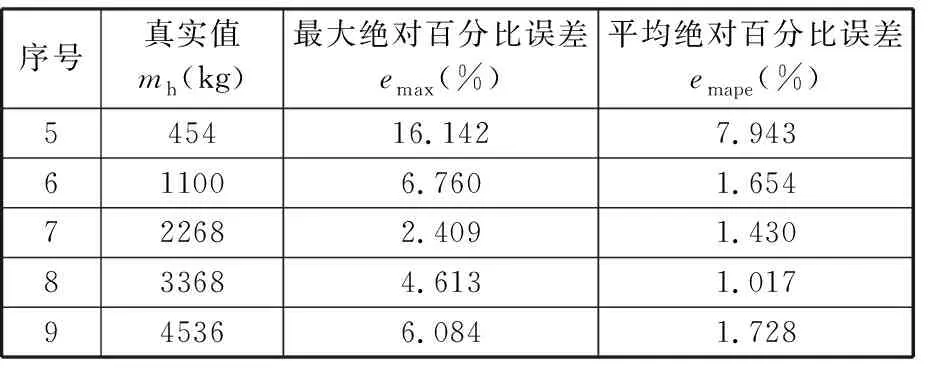
表5 辨識遞推前后載重估計的絕對百分比誤差

為驗證本文所提出的載重估計算法解決數(shù)據(jù)飽和現(xiàn)象的性能表現(xiàn)，以及更換載重或載重發(fā)生較大幅度變化時，該算法能否快速收斂到相應載重的真實值，即載重估計系統(tǒng)達到穩(wěn)定估計值的響應時間是否很短，進行了更換不同載重的在線試驗。伸縮臂叉車載重發(fā)生變化時的在線試驗如圖19所示。

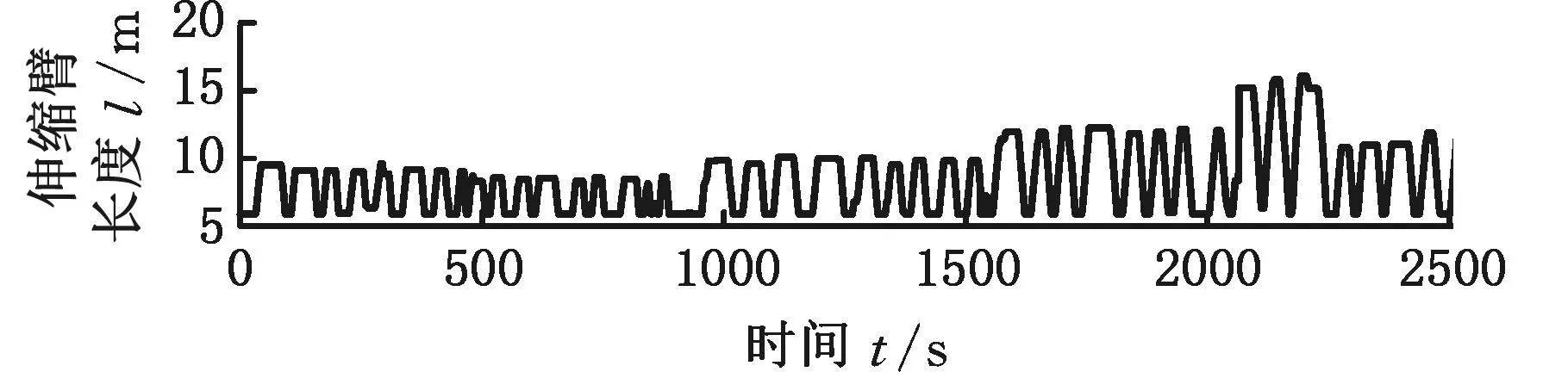
(a)伸縮臂長度

與圖5相比，由圖19可以看出，每當載重發(fā)生變化時，該系統(tǒng)不僅能夠自適應估計，而且能夠快速準確地辨識遞推到相應載重的真實值附近，趨于穩(wěn)定估計值的響應時間可以在1 s之內。

4 結語

本文在伸縮臂叉車工作裝置的結構組成和工作原理的基礎上，建立了基于動力學的載重估計數(shù)學模型，并推導出了載重計算公式，然后將該公式作為卡爾曼濾波算法的測量更新方程，將載重估值作為預測更新方程的狀態(tài)變量，對數(shù)學模型進行求解。最后，通過不同載重的離線試驗和在線試驗，得出以下結論：

(1)將載重估計作為一個模型辨識和參數(shù)估計的問題來處理，即根據(jù)動力學原理和伸縮臂叉車工作裝置的幾何結構關系，推導出一個含有未知參數(shù)的數(shù)學模型，然后用基于卡爾曼濾波算法遞推辨識載重的估計值，此種通過液壓缸壓力值間接估計載重的方法具有可行性和可靠性。對于454 kg的輕載荷，其估計結果的最大絕對誤差小于91 kg，而對于1100 kg、2268 kg、3368 kg和4536 kg的重載荷，其平均絕對百分比誤差小于3%，而且估計系統(tǒng)穩(wěn)定性好。該估計方法模型簡單、可移植強，可以擴展應用到吊車、門座起重機等工程機械的載重估計領域，對工業(yè)領域的自動化、智能化具有一定的實際應用意義。

(2)經過在線試驗驗證，本文所提出的基于改進卡爾曼濾波的載重估計算法能夠解決因載重發(fā)生突變以及大量新測量數(shù)據(jù)失去而對載重估值進行校正的數(shù)據(jù)飽和問題。當載重發(fā)生變化時，該算法能夠自適應且快速準確地辨識遞推到相應載重的真實值附近，趨于穩(wěn)定估計值的時間可以在1 s內。

本文針對伸縮臂叉車工作載荷快速準確估計方法進行了初步的理論分析和試驗驗證，但由于研究內容涉及的范圍較為廣泛，對影響該方法的一些其他因素和情況未能進行更加詳細和深入的研究。后續(xù)可以從以下幾個方面進行進一步研究：

(1)在建立基于動力學的數(shù)學模型時忽略了液壓油溫度、摩擦力和工作裝置磨損度等因素。不同溫度下液壓系統(tǒng)液壓油黏度等特性會發(fā)生變化，從而改變液壓缸液壓力，但是影響不大，一般可以采用強制預熱的方法解決；而摩擦力主要產生于工作裝置各個鉸接點處，特別是臂架與車架的鉸接點，為了減小誤差，可以考慮在工作載荷估計數(shù)學模型引入補償系數(shù)。這些因素還會影響工作載荷估計數(shù)學模型中的四個未知參數(shù)，而本文采取的是離線辨識，為了避免需重新辨識參數(shù)而造成的麻煩，還需研究在線辨識未知參數(shù)的情況。

(2)由離線試驗和在線試驗的試驗結果可知：當進行變幅和伸縮動作或以較高速度突然變幅提升重物時，由于慣性沖擊等作用會造成液壓系統(tǒng)壓力的不穩(wěn)定，導致工作載荷的絕對百分比誤差會比較大；在初始階段或變幅角度最大處時，由于伸縮臂處于變幅的極限位置或者叉具觸碰地面等情況，導致臂架受力比較復雜，通過工作載荷估計算法辨識遞推得到的工作載荷估計值也會有相當大的波動。為此，可以在伸縮臂上安裝霍爾傳感器，在設定的變幅角度和伸縮長度條件下，自動采集液壓缸壓力數(shù)據(jù)，選擇數(shù)據(jù)中的某一區(qū)間作為估計系統(tǒng)的有效數(shù)據(jù)采樣區(qū)間，進而進一步提高估計的準確度。