基于改進(jìn)蟻群算法的危險(xiǎn)化學(xué)品運(yùn)輸路徑優(yōu)化

杜玟諦 張虹

北京信息科技大學(xué)信息管理學(xué)院 北京 100192

危險(xiǎn)化學(xué)品運(yùn)輸中的事故具有低概率、高危害的特性，一旦發(fā)生就會(huì)對(duì)生命和財(cái)產(chǎn)安全帶來極大的威脅，造成不必要的經(jīng)濟(jì)損失和社會(huì)影響。目前我國(guó)危險(xiǎn)化學(xué)品物流中存在重復(fù)運(yùn)輸、運(yùn)力的選擇不當(dāng)、運(yùn)輸?shù)陌霃竭^大[1]、管理效能不足和從業(yè)人員素質(zhì)比較低等問題，物流運(yùn)輸過程主要依賴于線下，整體管理覆蓋面比較窄，水平也較低。京F公司現(xiàn)有的運(yùn)輸模式就是依賴第三方物流公司，運(yùn)輸過程中的安全監(jiān)管面臨很大的困難，同時(shí)使用第三方物流公司的成本也較高。所以，對(duì)于路徑的長(zhǎng)度以及過路費(fèi)的計(jì)算需要專業(yè)的地圖軟件進(jìn)行快速的計(jì)算和預(yù)測(cè)。

近年來，國(guó)內(nèi)外學(xué)者對(duì)蟻群算法的路徑優(yōu)化問題和危險(xiǎn)品運(yùn)輸路徑優(yōu)化的問題已開展了一些研究。例如，楊錦冬[2]等提出了車輛分配和裝載的雙目標(biāo)路徑優(yōu)化；魏航[3]等解決了時(shí)變條件下多式聯(lián)運(yùn)有害物品運(yùn)輸?shù)淖疃搪穯栴}；Karkazis[4]等對(duì)運(yùn)用分支定界的算法危險(xiǎn)品運(yùn)輸路徑的優(yōu)化模型進(jìn)行了研究；Akgun[5]等對(duì)考慮天氣系統(tǒng)影響的危險(xiǎn)品運(yùn)輸路徑選擇問題進(jìn)行了研究。

1 問題描述與模型構(gòu)建

1.1 危險(xiǎn)化學(xué)品運(yùn)輸問題描述

由于危險(xiǎn)化學(xué)品的特殊性，大量危險(xiǎn)化學(xué)品在運(yùn)輸過程中存在潛在的風(fēng)險(xiǎn)，運(yùn)輸車輛在發(fā)生事故后對(duì)人們的生命財(cái)產(chǎn)及周邊環(huán)境的安全構(gòu)成極大威脅。所以，面對(duì)越來越多的關(guān)于危險(xiǎn)化學(xué)品運(yùn)輸車輛的事故，有些道路在最近幾年開始禁止危險(xiǎn)化學(xué)品運(yùn)輸車輛的通行，導(dǎo)致運(yùn)輸路徑經(jīng)常變化對(duì)成本的預(yù)測(cè)造成了很大的困難。目前百度地圖等導(dǎo)航軟件已經(jīng)增加了危險(xiǎn)化學(xué)品車輛的備案和導(dǎo)航服務(wù)，司機(jī)可以使用導(dǎo)航軟件提供的從配送中心到每一個(gè)顧客彼此之間的一到三條路線，躲避修路、封路等不確定因素造成的禁行風(fēng)險(xiǎn)。同時(shí)可以較為準(zhǔn)確地估算出從配送中心到每一個(gè)顧客彼此之間的距離和所要繳納的過路費(fèi)。

對(duì)危險(xiǎn)化學(xué)品的運(yùn)輸過程進(jìn)行研究，要從貨物裝載至車輛開始，使用符合指定條件并經(jīng)過檢查的合規(guī)的專用運(yùn)輸車輛，運(yùn)輸過程要保證安全和及時(shí)，同時(shí)要保證送到客戶指定位置，如客戶倉(cāng)庫(kù)等。我們可以把危險(xiǎn)化學(xué)品的運(yùn)輸問題看成一個(gè)配送中心的物流運(yùn)輸問題，危險(xiǎn)化學(xué)品進(jìn)入倉(cāng)庫(kù)后被相應(yīng)數(shù)量的運(yùn)輸車全部配送至客戶指定位置，從同一個(gè)倉(cāng)庫(kù)出發(fā)，在滿足每個(gè)客戶提出的需求后又返回該倉(cāng)庫(kù)。在保證運(yùn)輸安全的情況下，根據(jù)客戶指定的位置坐標(biāo)、需求量、高速過路費(fèi)等數(shù)據(jù)，以包括運(yùn)營(yíng)總成本最低為目標(biāo)，求解出一個(gè)從倉(cāng)庫(kù)出發(fā)并滿足所有客戶需求的物流配送優(yōu)化方案。

(1)危險(xiǎn)化學(xué)品倉(cāng)庫(kù)和客戶指定的位置坐標(biāo)已知，倉(cāng)庫(kù)為本企業(yè)自己的倉(cāng)庫(kù)，不需要租賃費(fèi)用，每個(gè)客戶的危化品需求量已知，每條路徑的高速過路費(fèi)已知，這些已知的條件已確定且不會(huì)再改變。

(2)運(yùn)輸路徑的起點(diǎn)為危險(xiǎn)化學(xué)品的倉(cāng)庫(kù)，當(dāng)運(yùn)輸車完成運(yùn)輸任務(wù)后返回到倉(cāng)庫(kù)，形成一個(gè)完整的物流運(yùn)輸路線。

(3)企業(yè)的同種類型運(yùn)輸車輛足夠多且滿足客戶的需求，車輛的油耗、司機(jī)的食宿費(fèi)用、車檢罐檢及保險(xiǎn)費(fèi)用、路徑上的限重等參數(shù)已知，車輛為每個(gè)客戶的配送量都小于自身限重。

(4)在運(yùn)輸過程中，為客戶提供服務(wù)時(shí)，除卸貨情況外沒有其他裝卸活動(dòng)。

(5)每輛車都可以配送多個(gè)客戶點(diǎn)，且只允許1輛車出發(fā)和到達(dá)1次。

(6)危險(xiǎn)化學(xué)品運(yùn)輸不允許混裝，除限重外不考慮道路因素對(duì)車輛的影響，每輛危險(xiǎn)化學(xué)品運(yùn)輸車容量有限，危險(xiǎn)化學(xué)品運(yùn)輸車輛夜晚禁行。

1.2 模型構(gòu)建

1.2.1 基本蟻群算法

蟻群算法來自螞蟻尋找食物，螞蟻會(huì)在其經(jīng)過的路線上留下自己的信息素，它們依靠信息素來進(jìn)行彼此的信息交流，從而找到到最優(yōu)的路徑。其中一條路徑爬行過的螞蟻越多，則該條路徑留下的信息素也就越多，當(dāng)后續(xù)有螞蟻尋找路徑時(shí)，它們選擇這種路徑的概率就越高，當(dāng)途經(jīng)的螞蟻?zhàn)銐蚨鄷r(shí)，信息素最多的路徑就是最優(yōu)路徑。

1.2.2 容量受限車輛路徑模型

容量受限的車輛路徑模型是指：在滿足一個(gè)顧客只能由一輛車對(duì)貨物進(jìn)行配送的前提下，配送中心派遣若干運(yùn)輸車輛為顧客配送貨物，每輛車都從配送中心出發(fā)，當(dāng)該條路徑上所有的顧客配送結(jié)束后返回配送中心，規(guī)劃出總成本最小的運(yùn)輸路徑。

使用蟻群算法求解容量受限的車輛路徑問題可以通過有向圖G=(V，A)來進(jìn)行描述，其中V={0，1，2，…，n，n+1}表示所有節(jié)點(diǎn)的集合，0和n+1表示配送中心，1，2，…，n表示顧客，A表示客戶之間、客戶與配送中心間的有向弧集合。問題規(guī)定在有向圖G上，每一條配送路線必須都從0這個(gè)節(jié)點(diǎn)開始，在n+1這個(gè)節(jié)點(diǎn)結(jié)束。

容量受限的車輛路徑問題[6]的模型如下。其中，Δ+(i)表示從節(jié)點(diǎn)i出發(fā)的所有弧的集合，Δ-(j)表示回到節(jié)點(diǎn)j的所有弧的集合，N=V(〗0，n+1}表示所有顧客的集合，K表示配送車輛集合；cij表示節(jié)點(diǎn)i和節(jié)點(diǎn)j之間的距離，di表示顧客i的需求量，C表示貨車的最大裝載量，M表示一個(gè)足夠大的正數(shù)；決策變量xijk表示貨車k是否從節(jié)點(diǎn)i出發(fā)前往節(jié)點(diǎn)j，如果是，則xijk=1，否則xijk=0。

(1)

(2)

(3)

(4)

(5)

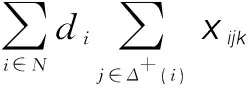
(6)

(7)

xijk∈{0，1}?k∈K，?(i，j)∈A

(8)

目標(biāo)函數(shù)(1)表示最小化車輛行駛的總距離；約束(2)表示每個(gè)顧客只能被分配到其中一條路徑；約束(3)～(5)限制配送車輛k在路徑上的流量；約束(6)表示初始在配送中心時(shí)，配送車輛的k裝載量不可以大于最大裝載量；約束(7)淘汰不經(jīng)過配送中心的子回路，其中集合S為集合N的子集。

2 改進(jìn)蟻群算法求解步驟

2.1 改進(jìn)蟻群算法

2.1.1 下一個(gè)顧客訪問概率

計(jì)算出從配送中心0轉(zhuǎn)移到下一個(gè)顧客的概率，螞蟻k從i點(diǎn)轉(zhuǎn)移到j(luò)點(diǎn)的概率計(jì)算公式如下：

(9)

2.1.2 輪盤賭法

蟻群算法中為了保證螞蟻選擇路徑的隨機(jī)性，在選擇路徑時(shí)概率大的路徑被選擇的概率大，但同時(shí)概率小的路徑也有可能被選中，而不是直接選擇概率大的路徑，這樣就不會(huì)所有的螞蟻到這里都做出同樣的選擇，導(dǎo)致算法失去隨機(jī)性。

為了避免算法失去隨機(jī)性，在選擇路徑時(shí)使用輪盤賭的方法來選擇。將每條路徑的概率看作是輪盤的一個(gè)扇面，旋轉(zhuǎn)輪盤，指針停在哪一個(gè)扇面上就選擇對(duì)應(yīng)概率的路徑，通過使用一個(gè)[0，1]之間的隨機(jī)數(shù)rand來模擬指針停止時(shí)指向的扇面。

2.1.3 信息素濃度更新方式

信息素濃度的更新方式是蟻群算法收斂效率的重要因素。更新信息素濃度主要有這幾方面：第一，信息素濃度與此路線的長(zhǎng)度有很大關(guān)系，為了防止該算法局部收斂過早，不能過多積累信息素，所以對(duì)信息素濃度的更新是很重要的；第二，信息素會(huì)隨著時(shí)間的推移而逐漸蒸發(fā)，該條路線上的信息素濃度就會(huì)降低；第三，該條路線的所有螞蟻經(jīng)過時(shí)都會(huì)釋放信息素，因?yàn)橄伻核惴ň哂姓答佇裕摋l路線越短螞蟻越多，信息素也就越多。為了將最優(yōu)路徑從全部的路徑中最快找到,文獻(xiàn)[7]通過尋找當(dāng)次迭代中的最優(yōu)路徑和最差路徑，加強(qiáng)最優(yōu)路徑上的信息素，同時(shí)減弱最差路徑上的信息素釋放量，按照式(10)方式的更新信息素，防止過快收斂導(dǎo)致算法陷入局部最優(yōu)。

(10)

上式中Lbest表示此次迭代中的最優(yōu)路徑長(zhǎng)度，Lworst表示此次迭代中的最差路徑長(zhǎng)度，Q為信息素濃度的常數(shù)。針對(duì)以上改進(jìn)的信息素更新方式，將提出的信息素濃度更新的方案與基本蟻群算法相結(jié)合，從而提出一種新的改進(jìn)蟻群算法。

2.1.4 運(yùn)輸成本

(11)

其中，cost表示運(yùn)輸成本；tollijk表示貨車k從節(jié)點(diǎn)i到節(jié)點(diǎn)j所需的過路費(fèi)；OP為當(dāng)前油價(jià)；salaryk表示貨車k對(duì)應(yīng)的司機(jī)等工作人員的工資及餐補(bǔ)。

2.2 求解步驟

STEP1：設(shè)m為螞蟻的數(shù)目，maxgen為最大迭代次數(shù)，s為配送中心，α為信息素重要程度因子，β為啟發(fā)函數(shù)的重要程度因子，ρ為信息素?fù)]發(fā)因子，Q為螞蟻構(gòu)建一次完整路徑所釋放的信息素總量。

STEP2：輸入配送中心和n個(gè)顧客的坐標(biāo)數(shù)據(jù)。輸入依據(jù)地圖軟件測(cè)算出的配送中心與n個(gè)顧客彼此之間的距離和所要花費(fèi)的過路費(fèi)。

STEP3：初始化信息素矩陣和螞蟻路徑記錄表，初始迭代次數(shù)計(jì)數(shù)器gen=1。

STEP4：判斷迭代次數(shù)gen是否大于最大迭代次數(shù)maxgen。如果gen大于等于maxgen，則執(zhí)行STEP8；如果gen小于maxgen，則執(zhí)行STEP5。

STEP5：從第一只螞蟻開始，根據(jù)輪盤賭法和轉(zhuǎn)移概率計(jì)算公式，求出每一只螞蟻下一個(gè)訪問的顧客，并記錄至路徑記錄表，構(gòu)建螞蟻的行走路線。

STEP6：將完整路徑轉(zhuǎn)換為配送方案，并計(jì)算出每種方案的總距離，從而計(jì)算出每種方案的總成本。

STEP7：在m只螞蟻所規(guī)劃的方案中找到最好的一個(gè)方案，更新此方案所包含的線路上的信息素，并將迭代次數(shù)gen增加1，執(zhí)行STEP4。

STEP8：輸出最佳配送方案。

3 實(shí)證分析

本文使用matlab2020a進(jìn)行仿真實(shí)驗(yàn)，以京F公司的危險(xiǎn)化學(xué)品運(yùn)輸?shù)穆窂絻?yōu)化問題，說明本文中將新的信息素更新方法融入基本蟻群算法后，形成的改進(jìn)蟻群算法在解決危險(xiǎn)化學(xué)品車輛路徑問題時(shí)的可行性和有效性。

3.1 利用基本蟻群算法求解

基本蟻群算法求解時(shí)的參數(shù)設(shè)置為迭代次數(shù)Maxgen=100，最大裝載量C=40，螞蟻數(shù)量m=50，信息素重要程度因子α=1，啟發(fā)函數(shù)重要程度因子β=5，信息素?fù)]發(fā)因子ρ=0.85，信息素濃度常數(shù)Q=5。

利用基本蟻群算法求解京F公司的容量受限的危險(xiǎn)化學(xué)品運(yùn)輸路徑問題時(shí)，得到的結(jié)果如下(圖1、圖2)所示：

圖1 普通蟻群算法最優(yōu)路徑

圖2 普通蟻群算法迭代次數(shù)

使用基本蟻群算法求解京F公司的容量受限的危險(xiǎn)化學(xué)品運(yùn)輸路徑問題，車輛使用數(shù)目為3輛，車輛行駛總距離為6479km，總成本為80830元。

3.2 利用改進(jìn)蟻群算法求解

改進(jìn)蟻群算法求解時(shí)的參數(shù)設(shè)置同上。利用改進(jìn)蟻群算法求解京F公司的容量受限的危險(xiǎn)化學(xué)品運(yùn)輸路徑問題時(shí)，得到的結(jié)果如(圖3、圖4)所示：

圖3 改進(jìn)蟻群算法最優(yōu)路徑

圖4 改進(jìn)蟻群算法迭代次數(shù)

使用改進(jìn)蟻群算法求解京F公司的容量受限的危險(xiǎn)化學(xué)品運(yùn)輸路徑問題，車輛使用數(shù)目為3輛，車輛行駛總距離為6211km，總成本為75040元。

將兩種方法的結(jié)果進(jìn)行對(duì)比，基本蟻群算法的路徑為：車輛1：0→5→6→8→7→11→4→0；車輛2：0→12→9→3→1→2→0；車輛3：0→10→0。在第49次迭代時(shí)，得到了最優(yōu)解，車輛行駛總距離為6479km，總成本為80830元。改進(jìn)蟻群算法的路徑為：車輛1：0→10→8→4→6→7→11→0；車輛2：0→12→9→3→1→2→0；車輛3：0→5→0。在第23次迭代時(shí)，得到了最優(yōu)解，車輛行駛總距離為6211km，總成本為75040元。

本文改進(jìn)的蟻群算法使得運(yùn)輸總成本比基本蟻群算法降低了5790元，行駛總距離降低了268km，最優(yōu)解迭代次數(shù)減少了26次。不管是在行駛距離、計(jì)算效率還是在總成本上都有較大的優(yōu)勢(shì)。

4 結(jié)論

由于運(yùn)輸過程中可能出現(xiàn)路況變化等問題，變更運(yùn)輸路線的情況變得越來越常見，司機(jī)們也開始熟練運(yùn)用專業(yè)地圖軟件進(jìn)行導(dǎo)航，從而規(guī)避堵車等原因臨時(shí)交通管制等風(fēng)險(xiǎn)。由于危險(xiǎn)化學(xué)品運(yùn)輸車輛的容量有限，而客戶的需求總量又比一輛車的容量多，隨著現(xiàn)有道路對(duì)大型危險(xiǎn)化學(xué)品運(yùn)輸車輛的限制越來越多，危險(xiǎn)品運(yùn)輸車輛的運(yùn)輸路徑優(yōu)化變得越來重要。本文使用的改進(jìn)蟻群算法可以更快收斂，更快地計(jì)算出總距離最短、總成本最少的路徑，可以有效運(yùn)用于解決京F公司的危險(xiǎn)化學(xué)品運(yùn)輸問題。