數值模擬在連續介質力學教學中的應用

常孟周，李璐璐，范飛高

（沈陽理工大學瞬態物理力學與能量轉換材料重點實驗室，遼寧 沈陽 110159）

0 引言

連續介質力學是普遍適用于物質四態（固態、液態、氣態以及等離子態）的力學理論，是力學學科最重要的理論基礎之一，由法國數學家奧古斯丁·路易·柯西于19世紀提出[1]。連續介質力學主要研究質量連續分布可變形物體的變形與運動規律，并討論一切連續介質普遍遵從的力學規律，例如，質量守恒定律、動量和角動量定理、能量守恒定律等[2]。

連續介質力學是我校力學/火炮、自動武器與彈藥工程/武器系統與運用工程/兵器工程專業學位研究生的一門專業方向課，以力學理論為主框架，為后續彈性力學、彈塑性力學以及工程流體力學等相關課程的開展奠定了理論基礎。

《連續介質力學》以物理力學為基礎，以復雜的數學運算為方法，授課內容廣泛、問題抽象，且系統性、理論性與邏輯性較強，許多理論需要借助多媒體教學（PPT、視頻等）展示大量圖形與數學物理實證，便于學生理解與解釋。連續介質力學的課堂教學中，基本概念與重要公式較多，并且許多公式與定理的推導過程十分復雜，采用傳統板書教學，具有理論推導講解與呈現同步的特點，但并不能生動形象展示本課程的抽象概念。可借助數值模擬的方法進一步將張量、應力應變、變形位移等內容具體化，提高學生的積極性。

1 數值模擬軟件簡介

結合我校力學/火炮、自動武器與彈藥工程/武器系統與運用工程/兵器工程專業的學科設置特點與研究方向，重點介紹ABAQUS、LS-DYNA、AUTODYN以及COMSOL等數值模擬軟件[3]。

ABAQUS是廣泛應用于工程模擬的有限元軟件，可以進行相對簡單的線性分析與復雜的非線性分析。尤其針對工程上常用的材料，如金屬、橡膠、復合材料以及土壤巖石等，ABAQUS憑借其豐富的材料庫與分析模塊成功分析了復雜載荷下諸多材料的結構力學特性。此外，ABAQUS軟件還可以解決其結構優化、熱傳導以及多物理場耦合等問題。

LS-DYNA則以其強大的通用非線性功能而聞名于世，能夠較真實地模擬復雜非線性問題，具有匹配材料與結構的大變形、損傷斷裂以及表面接觸的物理現象的多種物理模型，可用于解決多結構、多步驟以及多尺度的結構動力學問題。目前，LS-DYNAY已經廣泛應用于航空航天、汽車、船舶、電子、土木工程等領域。與LS-DYNA相比，AUTODYN具有豐富的炸藥材料庫，更擅長處理爆炸、沖擊等流-固-流復雜耦合問題，在高速、瞬態動力學的分析領域占據領先地位。

與上述軟件相比，COMSOL軟件內部預制多種物理場模型與數學模型，可以任意設置物理場之間的耦合形式，實現力學、熱力學、聲學、光學以及電磁學等方面的耦合仿真分析。

2 材料本構模型

應力與應變之間的物理關系，即本構關系，對應的函數即本構方程。結合本課程授課重點，選取典型彈性本構模型、彈塑性本構模型以及超彈性本構模型進行研究[4]。

2.1 彈塑性本構模型

2.2 超彈性本構模型

橡膠類材料通常具有不可壓縮性、大變形以及非線性等特點，可采用基于應變能函數的唯象模型表征其力學行為，例如，Mooney-Rivlin模型、Yeoh模型、Valanis-Landel模型以及Ogden模型等。

Yeoh模型具有形式簡單、精確度高的優點，其材料參數可通過單軸壓縮實驗確定，Yeoh模型應變能密度函數U表達式為

3 算例分析

案例：正方形板均勻地由構型I變形至構型II，確定拉格朗日應變分量E與歐拉應變分量e。

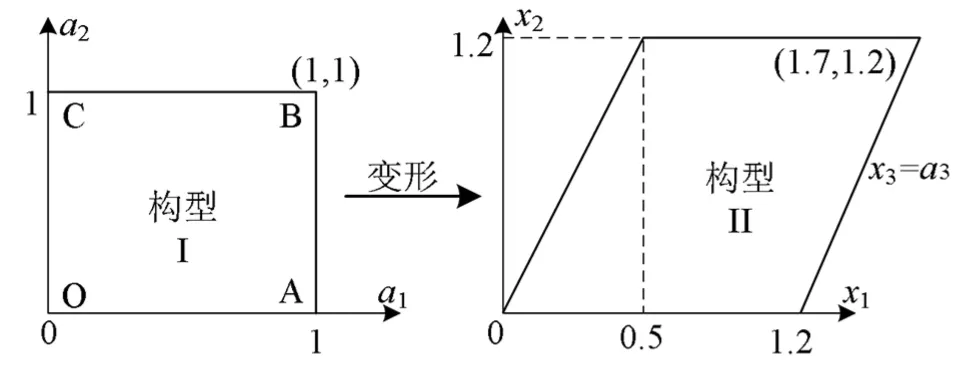
圖1 典型案例分析

此外，針對小變形情況，可將上述公式簡化為

采用傳統的公式計算方法可以獲得案例的整體應變，但無法直觀觀測材料的應力、應變分布特性。考慮到課堂實例的普遍性與基礎性，可采用上述任意一款數值模擬軟件對材料的應力應變場進行分析。本文選取 COMSOL Multiphysics，對案例的應變與應力分布特性進行分析。

對于各向同性彈性材料（以6061 Al為例），取參數E=71GPa，，；對于各向超彈性材料（以橡膠為例），取參數C10=0.6465MPa，C20=-0.3968MPa，C30=0.2040MPa[5]。數值模擬過程中，通過設置邊界OA、AB、BC與OC的變形定義邊界條件。圖2為各向同性彈塑性材料的應力應變數值模擬結果（上標e表示彈性，上標p表示塑性）。

圖2 各向同性彈塑性材料的應力應變數值模擬結果

此外，分析圖2（b）與圖2（c）可知，在構型II條件下材料已發生塑性變形，基本保持一致。應變分析可知，彈性應變均在10-3量級，與發生塑性變形對應的變形值匹配；而塑性應變，與表現出明顯的不均勻分布特性，且三者的平均值分別為0.17，0.27與0.24。

此外，超彈性材料由于其剛度小、抗剪切能力弱且易大變形的特點，基于COMSOL數值模擬得到的應力應變分布特性均呈現均勻分布狀態，且，，與，不再贅述。為了進一步闡明材料特性對變形特點的影響，設置AB與OC的變形條件，而將OA與BC設置為自由狀態，研究不同類型材料的應力應變特性。以超彈性材料為例，其應力分布如圖3所示。

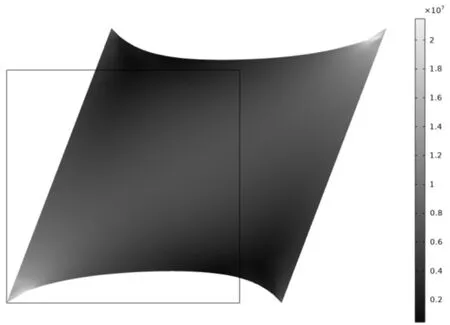
圖3 超彈性材料的應力分布特性

分析可知，各向同性彈性材料的OA與BC邊發生內凹，而最大應力值出現在O，B點處；而塑性材料發生了明顯的屈服變形，且大部分塑性變形集中于AB、OC邊界以及中間區域，而OA與BC邊表現出彈性變形；對于超彈性材料而言，其變形特性與彈性材料類似，但最大應力值對應區域更加明顯。

4 結論

針對連續介質力學教學中數理基礎要求高、公式推導多、概念抽象以及學生理解不深刻等問題，將數值模擬方法引入教學中，結合難度適宜的實例分析，一方面利于學生具體形象地理解連續介質力學中的基本概念，有效提高課堂教學效果；另一方面，數值模擬方法的應用可進一步提升研究生的專業技能。