結構化學材讓學習趨向“整體”

左小平

摘要：強調課程內容結構化，就是要通過結構化實現知識的整體建構。數學知識比較抽象，結構化學材能夠避免知識的分散、割裂現象，促進知識的整體感知、有效理解，因而成為學生學習的有益支架。結構化學材，讓學習內容趨于整體系統，讓學習過程實現整體關聯。

關鍵詞：小學數學；結構化學材；整體系統；整體關聯

*本文系江蘇省基礎教育內涵發展項目“小學數學結構化學習課程基地建設”的階段性研究成果。

《義務教育數學課程標準（2022年版）》（以下簡稱“新課標”）強調的課程內容結構化，就是要通過結構化實現知識的整體建構，從而便于發現知識的意義和價值。數學知識比較抽象，結構化學材能夠避免知識的分散、割裂現象，促進知識的整體感知、有效理解，因而成為學生學習的有益支架。結構化學材，讓學習內容趨于整體系統，讓學習過程實現整體關聯。下面，結合《小數的初步認識》一課教學具體闡述。

一、結構化學材讓學習內容趨于整體系統

結構化學材有著清晰的知識脈絡結構，能夠幫助學生在知識的整體與局部、本質與現象的聯系中掌握知識。學生在使用學材的過程中，不斷經歷知識內化、凝聚的建構過程，不斷理解、把握知識的系統性。

“小數的初步認識”是“數的認識”這一核心板塊的重要內容。教學時，可以站在“數的認識”的高度設計學材，突出學習內容的系統性。通過“你知道0.3表示什么意思嗎？選擇1—2個學材表示0.3的意思，并用簡短的語言記錄下來”的大任務驅動，學生不斷地建構“小數”的整體概念。

課堂中，為學生提供一組結構化學材：1米長的線段和1元的硬幣，對接學生的生活經驗，這是形象的學材，帶領學生由生活體驗進入數學學習；一個長方形，對接學生的學習經驗，這是半抽象的學材，有效地引導學生由感知到想象，再到抽象；一處空白，讓學生自創學材，這是一個開放的、抽象的學材，體現學生對生活問題數學化的理解，激發學生自我的數學對話。

涉及結構化學材的理解與應用包含三個步驟：

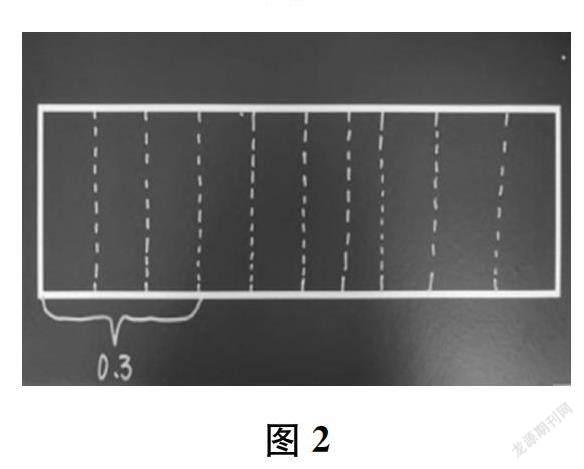
首先，展示不同的學材。先呈現“1米的線段”，學生對長度單位已有相當豐富的經驗，能夠根據1米等于10分米，聯想到把1米平均分成10份，其中的3份就是0.3。再呈現“1元的硬幣”（如圖1所示），學生根據生活經驗，用“1元等于10角，0.3元就是其中的3角”來表達自己對0.3的理解。最后呈現“一個長方形”（如圖2所示），有的學生將長方形平均分成3份，認為其中的1份就是0.3。在交流中，引導學生發現，平均分成10

份，其中的3份是0.3。進而，讓學生明白為什么要將這些學材分一分，即“0.3是小于1的數”，并在操作中自然體會到小數與整數的聯系。

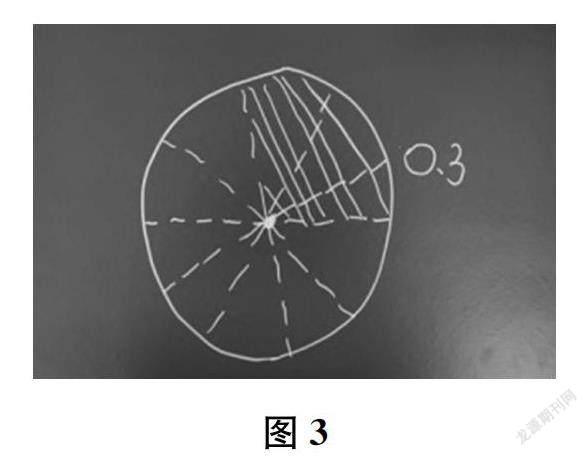
其次，展示學生創造的學材。學生的經驗是創造的源泉，教師要對接小數的意義理解，促地學生對經驗的“重構”。課堂中，有學生創造了“圓形比薩”（如圖3所示），將一個比薩平均分成10份，表示其中的3份就是0.3。此外，有學生創造“正方形”，有學生創造“一個西瓜”，等等。多樣的學材豐富了學生對0.3的理解。

最后，在對比中初步建構0.3的意義。一是通過“為什么這些不同的學材都能表示0.3？這些0.3又有什么不同？”的討論，讓學生實現對小數意義一般化的理解，即系統地理解“將一個物體平均分成10份，表示其中的3份就可以表示0.3”，而具體情境中“0.3”的意義卻是不同的。二是關聯舊知，引導“像這樣的描述，以前我們用哪個數來表示”，拓展小數一般化理解的應用。這樣，促進了學生對小數是十進分數的“一致性”理解。而“做”的經歷，對小數的模型建構起到了重要作用。

知識存在于“整體—部分—整體”之中，“部分”的知識深深地嵌于“整體”的學習之中。上述結構化學材，有坡度、有廣度、有深度，讓學生從整數“1”到分數“110”再到小數“0.1”，看到了不同形式數的內在聯系，構筑起整數、十進分數、小數之間的本質關聯，讓學生從“數的認識”的整體角度理解小數。

二、結構化學材讓學習過程實現整體關聯

結構是系統的屬性，是元素及關系的整體關聯。結構化學材作用于學生主體，促進學生對知識元素及元素之間關系的理解，讓學習過程變得整體關聯，并促使學生實現對認知的自主建構。［1］

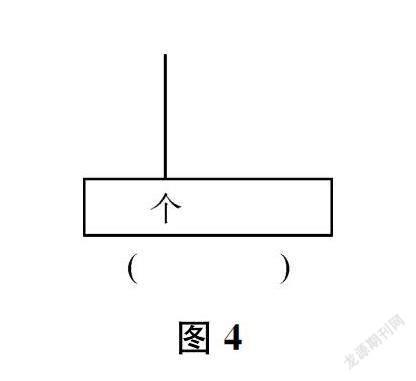
《小數的初步認識》一課，學生創造的學材（如圖4所示）就是為了產生“0.3”的表象。教師要以學材為載體，將學生對小數的認知納入數的體系中，以此豐富學生學習小數的過程，實現學習過程的整體關聯。這個特殊的計數器關乎的是數位、計數單位、十進制等，聯系的是小數與整數，使它們成為一個整體。這樣的結構化學材，依據小數核心元素之間的關聯，創造真實的學習情境，促進認識小數的過程實現由內而外結構化的理解。

通過“你能嘗試在計數器上表示出0.3嗎？”這一問題，引發認知沖突，引導學生創造“小數”。計數器上只有個位沒有小數，教師通過呈現學生的三類代表作品（如圖5所示），引導學生分類辨別正誤。對于第一幅作品，學生憑借已有經驗直接給出判斷。對于第二幅作品，學生借助此前利用不同學材表示0.3的經驗，自然聯想到在計數器個位上畫一顆珠子就表示1，把這顆珠子平均分成10份，然后取其中的3份，就是0.3。而有學生認為，在計數器上無法將1顆珠子平均分成10份，于是創造了一個數位，即在個位的右邊畫一個“豎桿”來表示，得到第三幅作品。他們是這樣理解的：“個位上肯定是0，在它右邊畫一個豎桿，0.3就在個位后面的數位上畫3顆珠子。”學生在對不同作品的思辨中將數與數位結合起來思考，使每一個數在計數器上都能找到表示的方法，實現了對小數的深入認識。

學生在嘗試中創造出了新的計數器。三類代表作品的解讀層層遞進，無不關聯到“小數”這一概念的核心元素。學生創造的這個數位是什么并不重要，重要的是學生從內心認可了十進制。計數器中的自由表達，將學生初步感受小數的數位、計數單位、十進制這些元素的過程，與整數的數位、計數單位、十進制之間的聯系實現了整體關聯，從而真正意義上將小數納入整數的學習體系，體現“數的認識”體系的不斷發展與完善，促進學生學習的正遷移。

參考文獻：

［1］ 吳玉國.小學數學結構化學習的實踐研究［M］.南京：江蘇鳳凰教育出版社，2021：1.