基于虛擬再入角的快速離軌制動制導方法

權申明 , 王竹 晁濤 楊明

(1. 哈爾濱工業大學 控制與仿真中心，黑龍江 哈爾濱150080; 2. 上海機電工程研究所，上海 201109)

0 引言

飛行器在再入點的狀態如再入速度傾角、再入位置、再入速度等，對飛行器在大氣層內的飛行狀態和飛行能力有至關重要的影響[1-2]。良好的再入狀態，對飛行器在大氣層內的駐點熱流密度、總加熱量等物理約束、滑翔飛行的調節能力產生積極的作用，同時能夠增加飛行器的安全性和穩定性，減輕制導控制系統的壓力。再入點各狀態約束值由飛行器設計的總體單位根據任務需求及飛行器性能計算得到，設計離軌段制導控制算法時可認為是已知的。

飛行器離軌制動段制導算法可以規劃出一條滿足再入點狀態的轉移軌道。為方便研究，在初步設計軌道時，通常假設飛行器在軌道轉移過程中可瞬間獲得所需的速度沖量且僅受地球中心引力場作用。

文獻[3]指出，良好的離軌制動飛行狀態是確保天地往返飛行器安全、準確返回既定著陸場區的前提。傳統鈍頭體再入返回艙，受到橫向機動能力和搜救能力限制，必須保證再入點有足夠的控制精度。離軌制動可以視為軌道轉移的一種形式，現有的軌道轉移軌跡規劃算法設計時，發動機主要有脈沖推力(視為瞬時脈沖)、小推力和有限推力三種形式。其中，基于脈沖推力的計算較為簡單，相對成熟的Lambert 制導算法可在較短時間內計算出變軌點的速度增量，然而實際飛行過程中，發動機難以提供任意大小的發動機推力；小推力軌道轉移通常用在深空探測等場景，推力較小，因此需要數日才能完成某任務；有限推力離軌制動形式在航天器返回、載荷釋放等場景下應用廣泛，對該問題的研究具有工程意義。具體地，有限推力離軌規劃又可分為逼近式策略以及優化式策略。

在逼近式策略方面，文獻[4]提出兩次“推-滑”的離軌制導策略，分析了推力沿不同方向施加時能量和動量矩的變化規律，給出臨界高度的計算公式及兩次“推-滑”的判斷條件。文獻[5]將離軌制動過程分成能量耗散段和閉路導引控制段，探討了在燃料隨機耗盡情況下推力方向對再入點參數的影響，分析了推力方向切換與能量窗口的關系。文獻[6]利用軌道瞬時根數進行離軌制動算法設計，將離軌制動問題轉化為制動起點的緯度幅角的單參數搜索問題，并考慮了J2 項攝動、初始狀態偏差、質量與推力誤差的影響。文獻[7]借鑒運載火箭能量管理的思路，為實現耗盡關機，將離軌制動過程分為能量耗散與閉環制導控制兩個階段，在運算效率與制導精度方面均有一定的提升。逼近式策略方面的研究基于機理分析，從能量角度設計制動方案，通常僅考慮再入點速度大小和方向約束，由于沒有考慮時間代價，傳統的逼近式策略難以滿足快速離軌需求。

在優化式策略方面，文獻[8]提出的方法能夠實現指定再入點位置的飛行器離軌任務，但在內層計算過程中需要反復調用求解非線性規劃求解器，因此難以實現制動速度的在線計算。文獻[9]考慮再入返回飛行器對再入點高度和再入角的要求，推算了離軌制動的軌道參數及所需速度增量，同時指出了慣性系速度傾角和地固系下的再入角差異較小。 文獻[10]針對建立了有限推力轉移軌跡優化的凸優化模型，并提出一種迭代逼近算法，但每步迭代計算中的凸優化求解耗時在1.24~3.23 s 之間，算法難以實現在線優化。文獻[11-12]針對燃料最優問題進行研究，在飛行器總體優化設計階段具有重要意義，能夠節約大量成本。文獻[13]基于最優控制理論推導了離軌機動的最優性條件，給出了協態變量和狀態變量的解析解，進而轉化為兩點邊值問題，但初值的選取對求解結果有較大影響。文獻[14]針對轉移時間最優和燃料最優兩種性能指標，將原問題轉化為非線性規劃問題，將Bezier 曲線法得到的結果作為初值，采用內點法與序列二次規劃算法進行求解，雖然對初值的計算進行了改進與優化，但是仍難以做到在線計算。文獻[15]分別針對共面、異面軌道轉移問題，研究了基于凸優化方法的軌跡規劃，并選用不同指標進行了軌道機動能力分析，但是算法實時性較差，難以工程實現。文獻[16]提出一種組合制導方法，前期采用燃料最優的開環策略，采用基于標稱軌跡的閉環制導，受開環控制的影響，該方法的調節能力有待進一步研究。文獻[17]針對動能彈垂直再入問題利用自適應偽譜法對有限推力制動與連續小推力制動兩種方式進行了研究。上述研究成果往往需要借助工具箱，如SNOPT、SQP、CVX 等[18]。

由以上分析可以看出，基于逼近式和優化式策略的離軌制動算法均存在一定的不足：逼近式策略算法簡單，計算效率高，易于工程實現，然而少有考慮時間最優的離軌需求；優化式策略可以求解同時考慮多個再入狀態約束下的快速離軌制動問題，然而優化計算效率較低，難以實時在線計算。隨著空間飛行器智能化需求的不斷提高，再入飛行任務已經從到達地面固定目標點，逐步向著覆蓋全球任意位置發展，因此傳統的固定點離軌制動、固定的再入難以適應這種需求。對于已經部署就位的航天器，其上所攜帶燃料固定，為了應對一定范圍內可變的任務要求，飛行器需要具備一定的再入點狀態調節能力。

本文研究在離軌制動任務確定之后，燃料有限情況下的多終端約束的時間最優離軌制動算法。本文的主要創新點如下：

1)結合優化算法的結果，通過其最優軌道形式，提出燃料約束情況下的有限推力快速離軌制動制導算法；

2)提出虛擬再入角的概念，將時間最優快速離軌制動問題參數化為虛擬再入角的求解，簡化優化問題；

3)為滿足離軌制導算法的實時性要求，本文所提出的離軌制動算法計算簡單、快速且具有較強的收斂性。

1 問題描述

飛行器軌道轉移示意圖如圖1所示。圖1中，M為飛行器接到任務時的位置，K為離軌制動初始位置，E為再人點位置，C為地球表面目標點，h為軌道高度，hf為離軌段終端高度。選取軌道轉移時間固定或能量最小等為指標后，可唯一確定出轉移軌道。

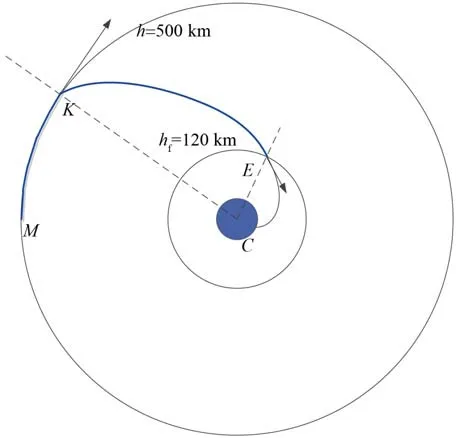
圖1 軌道轉移示意圖Fig. 1 Schematic diagram of orbital transfer

由于推力有限且連續作用，飛行狀態不能根據自由段解析彈道的特征解析計算，而是需要通過積分彈道方程來獲得。飛行器在大氣層外的運動模型可以描述為

式中：r為飛行器位置矢量，r為飛行器質心距地心的徑向距離，r=‖r‖；v為飛行器速度矢量；μ為地球引力常數；pe為發動機推力，pe表示制動推力大小；m為飛行器質量；Isp為發動機比沖；g0為地球表面重力加速度大小。

為了更加清晰地描述飛行器相對于地球的運動情況，給出慣性系下飛行器運動模型的另一種表示：

式中：v為飛行器相對地速；θ為飛行器速度傾角，在上為正；λ和φ分別為飛行器星下點的經度和緯度；χ為彈道偏角，順時針為正；α表示制動角，即推力方向與速度方向的夾角(類似于攻角的定義)；g為重力加速度，g=g0(R0/r)2，R0為地球平均半徑。

2 離軌制動算法設計

優化式策略通常基于最優控制相關理論，求解復雜、效率低，往往需要調用優化工具箱得到最優結果；逼近式策略基于能量守恒等原理，結合衛星軌道理論，實時計算可行的控制量，逐漸調整軌跡，可逐步逼近期望終端狀態。

2.1 沖量假設的離軌制動算法

沖量假設簡化了飛行器離軌制動的運動過程，認為飛行器可瞬間獲得需要速度，給離軌制動段的初步設計帶來了方便。

針對更加一般性離軌制動問題，飛行器一旦進入離軌制動階段，為實現高度的降低，飛行軌跡為橢圓軌道。

設v1為當前位置需用速度，r1表示由地心指向飛行器實時位置的向量，r2表示由地心指向期望再入點位置的向量，h0為飛行器離軌點高度，θ1為根據能量守恒和動量矩不變原理反求出r1處的期望速度傾角。沖量假設下的離軌制動問題描述為：已知r1處的初始速度v0和初始速度傾角θ0，r2處的終端速度v2和終端速度傾角θf，求解沖量假設下的離軌段制動參數Δθ和Δv，v1和制動速度的夾角為φ。矢量r1和r2的大小分別為r1和r2，v1和v2的大小分別為v1和v2。圖2 為橢圓軌道離軌段航跡示意圖。

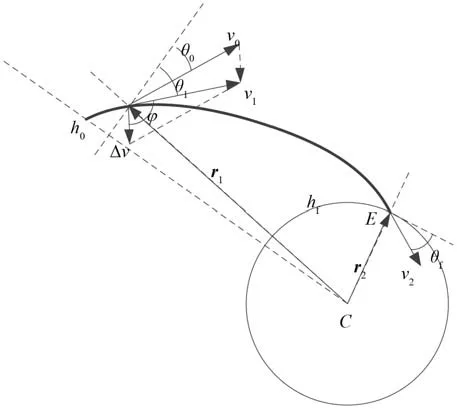
圖2 橢圓軌道離軌段航跡示意圖Fig. 2 Deorbit trajectory of an elliptical orbit

下面針對圖2 所示的任意橢圓軌道進行算法設計。根據能量守恒和動量矩不變原理，有

通過式(3)可以求解出θ1和v1，代入下式中：

由此可以得到離軌段制動參數Δθ和Δv，若能夠瞬時沿著φ的方向提供一個Δv，則飛行器將沿著新軌道運動，最終到達再入點。

2.2 有限推力離軌制動算法

通常情況下，天基再入滑翔飛行器的離軌制動發動機推力有限，因此2.1 節的沖量假設離軌制動制導方法難以適用。此外，即使發動機可瞬時提供任意方向及大小的推力，由于空間中攝動因素的存在，其離軌段終端將產生較大偏差，影響再入飛行。因此，采用有限推力方式的離軌制動制導方法研究更有實際意義，脈沖假設下的計算結果可作為參考。

由于燃料的消耗，飛行器質量不斷減少，根據給定的發動機參數，可以利用推力和比沖進行計算。

在有限推力模型中，采用沖量假設下的離軌制動制導方法，可以求解得到沖量假設下的離軌段離軌參數Δθ和Δv。在求解有限推力下的離軌段軌跡時，給定天基再入滑翔飛行器的制動點狀態及再入點狀態約束，計算推力大小與方向變化曲線，控制飛行器按照期望再入角、再入速度到達再入點高度。

結合2.1 節瞬時脈沖仿真結果，設計一種采用逼近式策略的考慮有限推力的制導步驟如下：

步驟1根據飛行器實時狀態、再入角度及速度，由式(3)按照瞬時脈沖方式確定出當前時刻所需的速度和角度信息。

步驟2結合飛行器當前角度和速度信息，計算制動速度Δv及制動角度。

步驟3沿著制動角度方向，改變飛行器速度增量為Δv，發動機采用最大推力。

步驟4若所需速度小于其設定閾值，即，則關閉發動機，飛行器沿橢圓軌道自由運動，否則循環步驟1~步驟3 的計算。

2.3 快速離軌制動算法設計

通過分析不難發現，以上兩種方法沒有考慮時間最優性指標，僅考慮了再入點高度、速度大小與速度傾角，因此求得的離軌制動軌跡難以滿足快速離軌的需求。

通過最優控制理論中的時間最優結論可知，時間最優情況下控制量通常是Bang-Bang 控制，類似于開關控制量，離軌制動階段飛行器所攜帶的燃料有限，因此假設時間最優的離軌制動問題中，制動發動機推力大小與制動角度形式如圖3 所示。圖3中，O點為原點，α軸表示制動角，t軸為時間，α1(t)為0~t1時間內的制動角變化曲線，α2(t)為t2~t3時間內的制動角變化曲線，pemax為最大制動推力，t1為制動發動機首次關機時刻，t2為第2 次開機時刻，t3為第2 次關機時刻，t4為到達再入點的時刻。

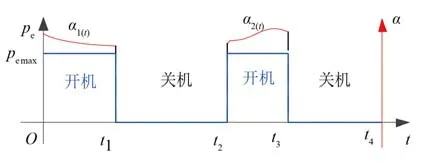
圖3 時間最優制動發動機工作狀態示意圖Fig. 3 Schematic diagram of time-optimal deorbit

求解α(t)，使得終端時間tf最小，同時滿足初始各狀態與終端各狀態，可描述為

式中：u為制動角變化曲線α(t)；Δm為飛行器總質量變化量；mfuel為燃料質量。

可將式(5)描述的問題轉化為非線性規劃問題，進而基于偽譜法進行求解，但是該類方法計算效率較差，工程實現性不強。還可將該非線性規劃問題轉化為凸優化問題，凸優化在求解最優控制問題的快速性與最優性上均有顯著提升[19]，然而現階段凸優化算法仍難以滿足在線實時計算的速度需求。

由于傳統的有限推力離軌制動算法并未考慮時間最優性，存在一定不足。設計改進的有限推力離軌制動算法如圖 4 虛線曲線所示，引入虛擬再入角的概念，在前期采用虛擬再入角，后期采用實際期望再入角作為約束。

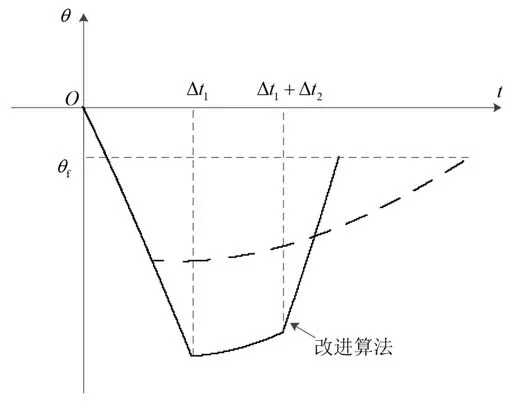
圖4 改進方法與傳統方法彈道傾角變化曲線示意圖Fig. 4 Curve of the flight path angle with the improved method and the traditional method

定義1虛擬再入角：

在再入返回的初期，設計不同于實際期望終端速度傾角θf的某固定或者時變再入角作為制導輸入指令，稱角度為虛擬再入角(在后期仍使用θf作為期望再入角)。

在離軌制動前期主要控制再入速度傾角與再入速度大小，后期根據文獻[4]中得到的垂直速度方向施加力不改變能量大小的結論，通過預測剩余燃料消耗時間，進行正推與反推的能量耗散策略。后期使用剩余燃料朝著目標點飛行，由于后期時間相對短，終端速度不會偏差太大。本文設計的快速離軌制動制導仿真流程如圖 5 所示。

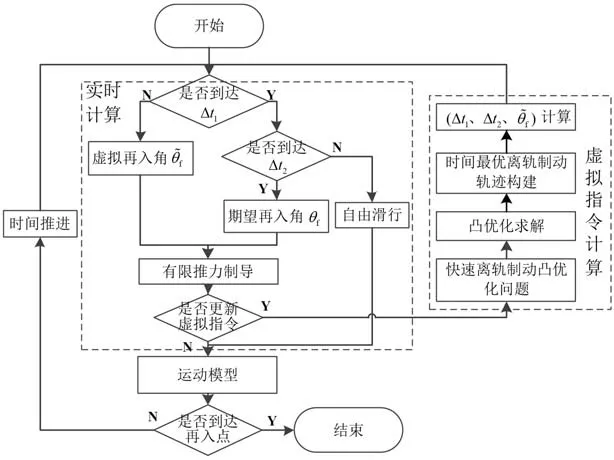
圖5 快速離軌制動制導仿真流程圖Fig. 5 Flow chart of simulation of fast deorbit guidance

因此，可將問題式(5)轉化為如下問題：

并使用凸優化方法對關鍵參數 Δt1、Δt2，以及第一階段的虛擬期望終端傾角求解。

基于沖量假設的有限推力下離軌制動算法存在的問題在于沒有考慮快速離軌的需求，但在再入速度傾角和速度大小的控制上，計算量小且精度較高。基于凸優化的離軌制動可以考慮時間最優約束，仍難以實時計算，但是通過與有限推力離軌制動算法相結合，將最優結果作為有限推力制動方法虛擬終端約束，從而給出快速離軌制動制導算法。

2.4 基于凸優化方法的子問題求解

文獻[19]給出了一種可以處理非線性等式的凸優化問題的方法。在時間最優的離軌制動問題中，給定起始時刻的高度、速度，要求飛行器以最短時間到達某一高度，并滿足終端的速度大小及傾角 要求。

使用凸優化對問題進行求解需要分為三個步驟。

2.4.1 狀態方程歸一化

式中：σ為松弛變量，代表推力-加速度。設狀態量為x=(r,v,z)T，控制量為u=(τ,σ)T，將狀態方程寫為如下矩陣形式：

當使用迭代方法求解最優解時，式(10)可看作線性方程。

2.4.2 求解初始軌跡

使用迭代方法求解時間最優離軌制動問題時，首先需要一條初始軌跡，在此基礎進行優化。

求解時間最優離軌問題，需要將離軌過程分為N段，每一段時間間隔為t0/N，求解N+ 1個狀態變量及控制變量。飛行器初始位置、速度與終端時刻位置、速度約束可表示為

離軌過程約束為式(9)~式(13)，由于地心距r為歸一化后的變量，在離軌過程中近似為1，在對結果精確度要求不高的情況下，式(9)中的r可近似為1，變為線性方程。

由于所有約束及目標函數均為凸的，此問題為一標準的凸優化問題。

2.4.3 迭代求解時間最優離軌制動問題

求解時間最優離軌制動問題不指定固定的再入點以及離軌時間，只要求到達固定的再入高度時滿足指定的速度大小及傾角，因此需要引入時間變量。此時式(9)與式(13)均為非線性等式約束。同時，為保證結果的精確，需要在初始解的基礎上進行多次迭代求解。

當凸優化問題中含有非線性等式約束hi(y) = 0,i= 1，… ,q時，假設當前迭代結果為y[k]，y= （f x,u,tf）。求解y[k+1]的過程如下：

在y[k]處對函數進行泰勒展開，hi(y) =0可以寫為

同時，又有展開式

凸優化問題的約束為

優化結果為yp，將在y[k]處1階展開：

式(18)兩側同乘(yp-y[k])T/2，得到

因此便將非凸約束hi(y) =0轉換為凸約束。

時間最優的離軌制動問題中，除了考慮式(9)~式(11)的約束之外，其余約束為

以離軌段終端時間tf最短為指標。式(9)的離散形式以及式(22)為非線性約束，將其按前述可得到凸函數的約束條件，并附加約束

即可求得y[k+1]以及u[k+1]，多次迭代直至收斂，得到時間最優離軌制動結果。

至此，將離軌制動問題轉化為凸優化問題，使用2階錐規劃方法進行求解，求解工具詳見文獻[20]。

2.5 基于最優軌跡的虛擬指令計算

根據凸優化求解得到的優軌跡中發動機推力大小曲線，可以看出時間最優的離軌制動問題中，控制量呈現“推-滑-推”的特點，從而根據其時間變化規律可得 Δt1、 Δt2，根據速度、傾角變化曲線，根據式(4)可以反求出虛擬再入角θ?f大小。

3 數值仿真及分析

考慮有兩臺推力發動機，每臺推力為500 N，比沖為300 s，離軌到再入階段單獨計算燃料質量，燃料為250 kg。

根據2.1~2.3 節給出的不同方法，考慮從某圓軌道進行離軌制動，初始高度h0=500 km，初始速度為v0=7 616.7 m/s，初始傾角θ0= 0°，期望終端高度hf=120 km、終端速度vf=7 950 m/s、終端傾角θf=-2 .5°為例，分別給出不同方法的仿真結果。需要指出的是，本文所提出的快速離軌制動制導方法采用類似的策略在橫向進行虛擬指令設計后，可適用于三維空間中的異面離軌制動，仿真中僅以縱向運動為例。

3.1 基于凸優化仿真結果

將快速離軌制動問題轉化為凸優化問題，進而使用2階錐規劃進行求解。仿真結果如圖6所示。通過多約束下時間最優離軌制動的仿真計算，可以看出飛行軌跡能夠實現時間最優的指標；從推力大小曲線可以看出，發動機工作狀態類似Bang-Bang控制，與最優控制的時間最優控制問題結果一致；由圖6(f)可以看出，飛行器終端時刻燃料用盡，終端各狀態滿足要求。同時，為了驗證方法有效性，放寬燃料限制，當燃料足夠時，推力可以長時間最大推力工作，通過改變制動角來實現時間最優指標。

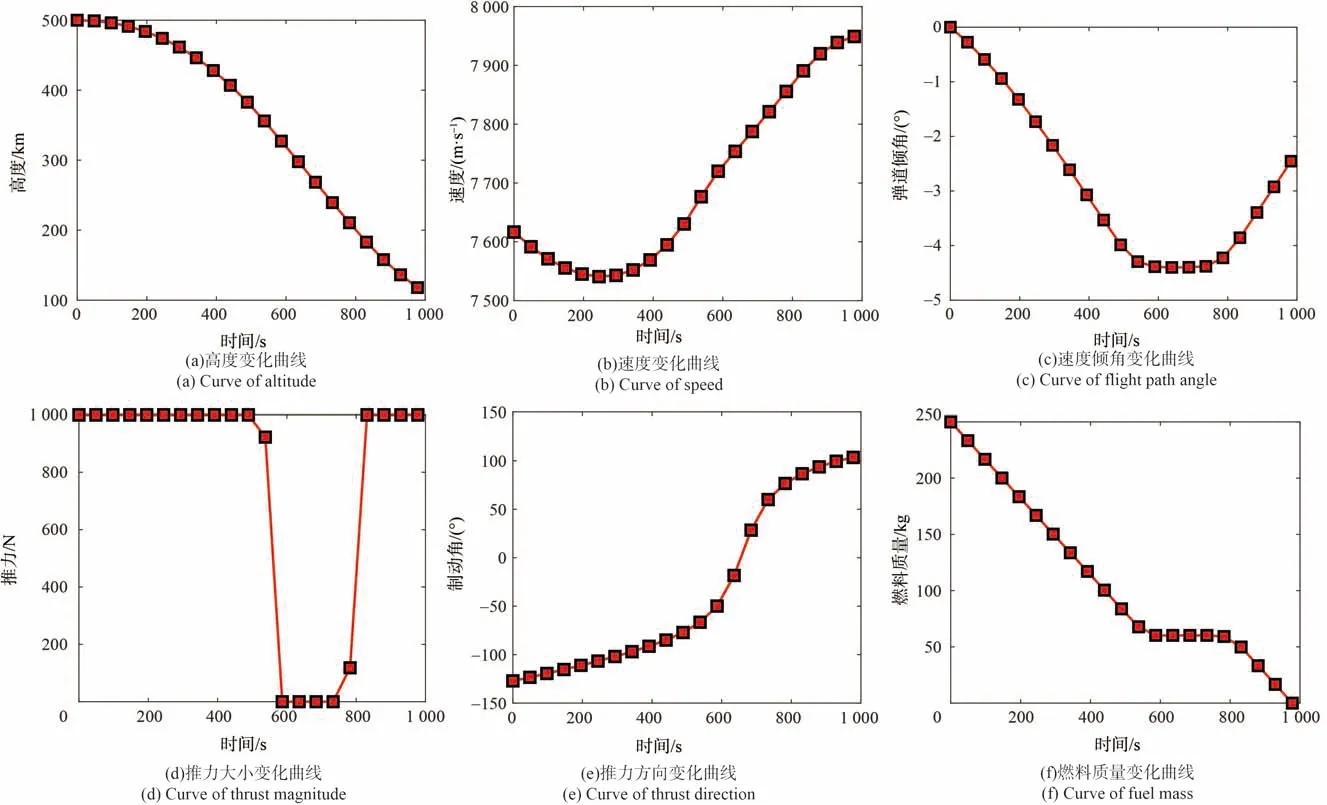
圖6 多約束下時間最優離軌制動狀態量變化曲線Fig. 6 Curves of time-optimal deorbit with multiple constraints

綜合以上仿真曲線可以看出，時間最優下的仿真結果雖比有限推力離軌制動的制動時間指標更優，但是從編程實現及運算效率上來看，代價較大。即使在初值合理的情況下，單次優化耗時在 1 s 以上，因此難以實現在線制導的目標。

3.2 快速離軌制動算法仿真

為驗證本文算法的有效性，選取不同終端狀態θf=-1 .5° 、θf=-2 .5° 、θf=-3 .5° 、θf=- 4.5° 進行仿真，基于文獻[6]中在線制導算法的仿真結果如圖 7 所示，基于本文快速離軌制動制導算法仿真結果如圖 8 所示。

對比圖7、圖8仿真結果曲線可以看出，兩種方法均能滿足終端高度、速度、傾角的終端約束。在傳統算法中，未考慮快速離軌制動需求時，燃料有剩余，且隨著終端傾角(幅值)的增大，離軌制動段飛行時間減小，燃料消耗增加，這是由于空間軌道中，速度方向的改變需要較大的速度增量。對比以上圖7(f)、圖8(f)子圖燃料質量變化曲線可知，為滿足離軌制動快速性的需求，本文算法能夠將燃料耗盡，離軌段節約時間最大值約為500 s。在計算效率方面，單步計算耗時均在5 ms以內，能夠滿足在線制導的需求。

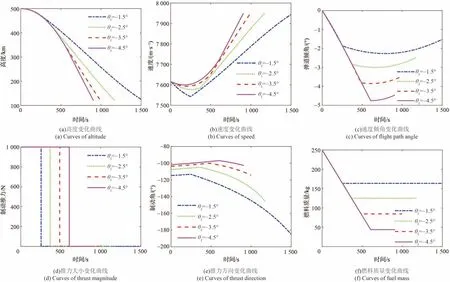
圖7 傳統離軌制動制導算法仿真結果Fig. 7 Simulation results of the traditional deorbit guidance algorithm

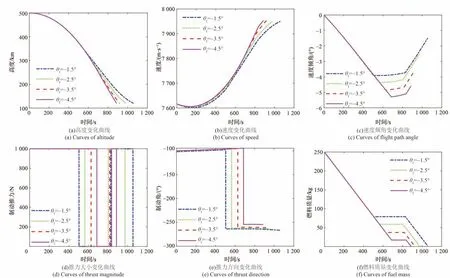
圖8 快速離軌制動制導算法仿真結果Fig. 8 Simulation results of the fast deorbit guidance algorithm

3.3 蒙特卡洛仿真

在實際離軌制動過程中，飛行器發動機受到各種偏差因素的影響，本文主要考慮推力大小攝動Δpe、推力方向攝動Δφ、燃料質量攝動Δm，各偏差均為均勻分布如表1 所示。

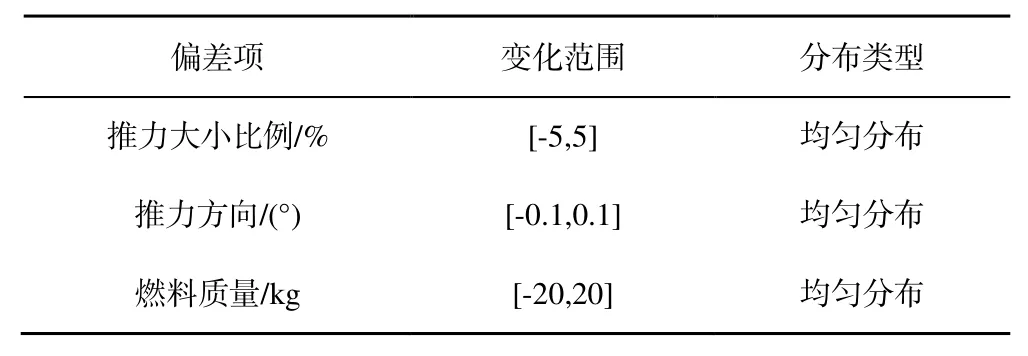
表1 參數攝動表Table 1 Parameter perturbations

進行1 000 組蒙特卡洛仿真實驗，仿真結果如圖 9 所示(Rf表示離軌制動段射程)。

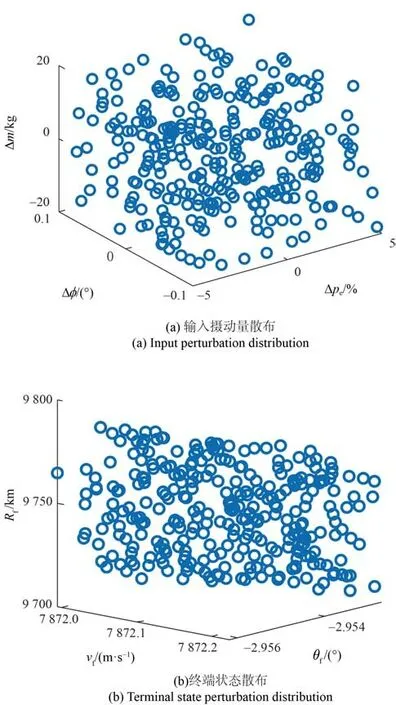
圖9 蒙特卡洛仿真參數散布圖Fig. 9 Distribution of Monte Carlo simulation parameters

根據終端狀態散布結果可以看出，該算法對終端速度與終端傾角控制精度較高，其中終端速度偏差為±0.2 m/s，終端傾角偏差為±0.002°。由于該算法未對射程進行精確控制，該狀態的絕對偏差較大為±50 km，然而該值相對于整個再入階段相對誤差較小，約為0.5%，同時考慮到后續的再入滑翔階段，對射程調節能力較強，因此離軌制動階段射程的影響可忽略。

4 結論

本文針對快速離軌制動的需求，提出基于虛擬再入角的快速離軌制動制導方法。借鑒固體運載火箭助推段末期的能量管理策略，通過設置合理的虛擬再入角與虛擬指令控制邏輯，設計“做正功”與“做負功”的切換規律，進行多余能量的耗散，可以實現快速離軌制動算法的在線設計。得出主要結論如下：

1)引入虛擬再入角的概念將離軌制動最優控制問題參數化，采用少次的凸優化方法求解最優軌跡進行虛擬再入角的更新，該算法相比于傳統凸優化方法具有計算簡單、運算效率高的特點。

2)相比于現有制導算法，基于虛擬再入角的快速離軌制動算法考慮了離軌耗時的因素，在燃料耗盡的情況下，能夠節約最多500 s 的離軌時長，滿足了離軌制動快速性的需求。

3)該算法對離軌階段發動機推力大小與方向、燃料質量攝動具有較強的魯棒性，再入點速度控制精度為±0.2 m/s，再入角控制精度為±0.002°。

在本文工作的基礎上，后續將考慮J2 攝動的快速離軌制動在線制導算法，考慮地球橢球體引起的非球形引力的等因素的影響，進一步增強本文算法的工程意義。