平面鏡中的角

沈冉

數學就在我們身邊。平面鏡是我們生活中熟悉的物品，其中也蘊含許多數學知識。下面就讓我們一起走近平面鏡，思考一道以“平面鏡”為背景的數學問題。

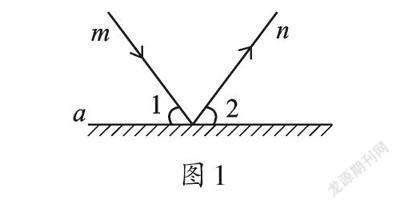
實驗證明：平面鏡反射光線的規律是照射到平面鏡上的光線和被反射出的光線與平面鏡所夾的銳角相等。如圖1，一束光線m射到平面鏡a上，被a反射后的光線為n，則入射光線m、反射光線n與平面鏡a所夾的銳角相等，即∠1=∠2。

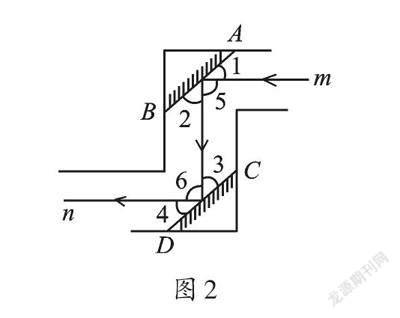
問題1：利用這個規律，人們制作了潛望鏡。圖2是潛望鏡工作原理示意圖，AB、CD是平行放置的兩面平面鏡。請解釋進入潛望鏡的光線m為什么和離開潛望鏡的光線n是平行的。

【解析】圖2中角比較多，我們要仔細觀察角與角之間的位置關系。由于AB∥CD，根據“兩直線平行，內錯角相等”，可知∠2=∠3。根據平面鏡的反射規律，可知∠1=∠2，∠3=∠4，∴∠1=∠2=∠3=∠4。而∠5=180°-∠1-∠2，∠6=180°-∠3-∠4，∴∠5=∠6。∴m∥n。理由是：內錯角相等，兩直線平行。

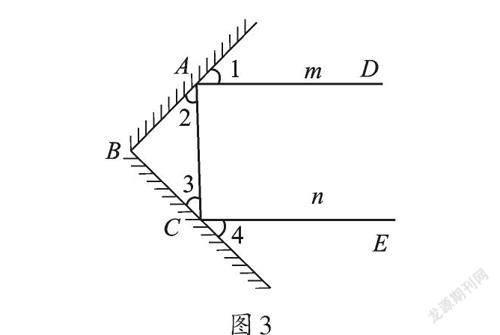
問題2：如圖3，改變兩個平面鏡之間的位置關系，經過兩次反射后，入射光線m與反射光線n之間的位置關系會隨之改變。若入射光線m與反射光線n平行，但方向相反，則兩個平面鏡的夾角∠ABC為多少度？

【解析】∠ABC是△ABC的內角，根據三角形內角和定理，可知∠ABC=180°-（∠2+∠3）。因此，只需求出∠2+∠3的度數即可。

∵m∥n，

∴∠DAC+∠ACE=180°。

又∵∠1+∠2+∠DAC=180°，

∠3+∠4+∠ACE=180°，

且∠1=∠2，∠3=∠4，

∴2∠2+2∠3=180°，

即∠2+∠3=90°。

∴∠ABC=180°-90°=90°。

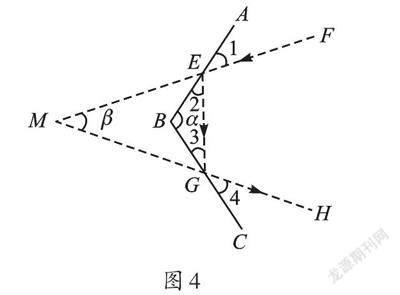
問題3：如圖4，若90°＜α＜180°，入射光線EF與反射光線GH的夾角∠FMH=β，請探索α與β的數量關系，并說明理由。

【解析】觀察圖4可以發現：∠FMH是△MEG的內角，∠ABC是△BEG的內角，這兩個三角形中的角都與∠2+∠3有聯系。根據“三角形內角和為180°”，可得∠2+∠3=180°-α。

又∵∠1=∠2，∠3=∠4（反射原理），

∠1=∠MEB，∠4=∠MGB（對頂角相等），

∴∠MEG+∠MGE=2∠2+2∠3=2（∠2+∠3）=2（180°-α）=360°-2α。

在△MEG中，β=180°-（∠MEG+∠MGE）=180°-（360°-2α）=2α-180°，

即β=2α-180°。

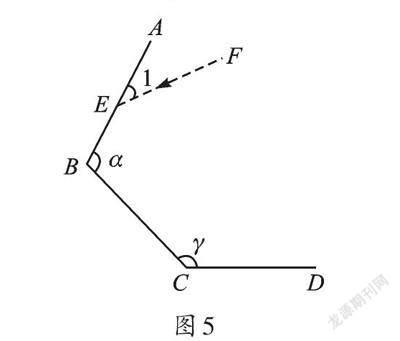
問題4：如圖5，若90°＜α＜180°，設鏡子CD與BC的夾角∠BCD=γ（90°＜γ＜180°），入射光線EF與鏡面AB的夾角∠1=m（0°＜m＜90°），已知入射光線EF從鏡面AB反射到鏡面BC，再反射到鏡面CD，最后經鏡面CD反射。當反射光線與入射光線EF平行時，探索m與γ的數量關系，并說明理由。

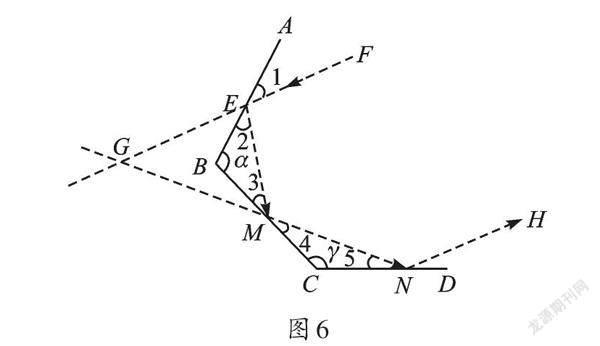
【解析】根據題意，畫出大致圖形，如圖6所示，延長NM和FE，交點為G。

由問題3的思路可得∠G=180°-2m-2∠3=180°-2（m+∠4），∠MNH=180°-2∠5。

∵EF∥NH，

∴∠G+∠MNH=180°，

即180°-2（m+∠4）+180°-2∠5=180°。

整理，得m+∠4+∠5=90°。

∴m+（180°-γ）=90°，即γ-m=90°。

本題還可以有其他思路，感興趣的同學可自行探究哦。