面向目標參數估計的雷達低峰均比穩健波形設計
李 響 李德煦 王俊偉 郝天鐸 曹興龍
(1.沈陽科技學院 沈陽 110000;2.93363部隊 沈陽 110000;3.國防科技大學 合肥 230000;4.93175部隊 長春 130000)
0 引言
波形設計是雷達的關鍵技術之一。在實際情況中,由于環境的非平穩特性和先驗知識估計方法的原因,使得雜波和目標的先驗知識并不準確,造成所設計波形與實際目標和雜波不匹配從而降低波形估計性能。因此,為了有效防止波形的估計性能下降,需考慮進行穩健波形的設計。此外,為了增強發射機對發射功率的利用率,現有文獻往往會考慮恒模約束。然而,恒模波形雖然是理想的發射波形,但其約束過于苛刻,往往為了便于實現,會轉向低峰均比(Peak-to-Average Power Ratio, PAR)約束下的波形設計[1]。因此,PAR約束下的穩健發射波形設計已成為認知雷達亟待解決的重要問題之一。
文獻[2]~[8]在先驗知識不準確時,對穩健波形的設計進行了研究,其所運用的準則主要基于最小克拉美羅界(Cramer-Rao bound,CRLB)準則、最大互信息(mutual information, MI)準則和最小均方誤差(Minimum Mean Square Error,MMSE)準則。文獻[2]~[5]以最小CRLB為優化準則進行穩健波形設計。張向陽[1]和周子昂[3]在MIMO雷達系統中對相關問題進行了研究,在白噪聲背景下,將信道誤差限定在一個超球體構成的不確定集內,分別采用不同的方法實現了非凸優化問題到凸問題的轉換,進而得到了MIMO雷達的穩健波形。H. Y. Wang[4-5]進一步假定信號與雜波無關,在雜波背景下采用半正定松弛(SemiDefiniteRelaxation,SDR)方法對MIMO雷達穩健波形協方差矩陣進行了設計。然而,這些文獻只考慮了信號無關雜波。此外,文獻[6]~[8]基于最大MI準則和MMSE準則對雷達穩健波形設計問題進行了研究。Y. Yang等人[6]較早地對此類問題展開研究,當目標的先驗知識不準確時,假定目標功率譜密度位于一個上、下界均已知的不確定集內,基于極大極小化準則進行了穩健波形設計E. Grossi[7]將目標的散射系數和目標的分布協方差矩陣限制在一個不確定集內,根據Schur補充定理[9]將非凸優化問題轉化為凸問題進行穩健波形的設計。但文獻[6]~[7]均未考慮雜波的影響。而T. Naghibi[8]彌補了這方面的不足,在其信號模型中加入了信號相關雜波,在目標散射系數不確定集范圍內進行了穩健波形設計。需要說明的是,以上文獻均未對波形進行恒模或者PAR約束。當對波形加以恒模或者PAR約束后,會使穩健波形設計問題變得較為復雜,現有文獻很少對此類問題進行研究。
針對該問題,以雜波沖激響應(Clutter Impulse Response, CIR)和目標沖激相應(Target Impulse Response,TIR)協方差矩陣特征值的不確定集表征CIR和TIR的波動范圍,基于極大極小化準則構建MI準則下的問題模型,在不確定集范圍內給出了MI最差情況下CIR和TIR的取值,并結合序列線性規劃(Sequence Linear Programming, SLP)方法實現了PAR約束下的穩健波形設計。
1 信號模型
本文主要以擴展目標為研究對象,考慮信號相關雜波背景下的波形設計問題。文中,用CIR表征相關雜波特性[11],用TIR表征目標散射特性[10],則時域信號模型如圖1所示。
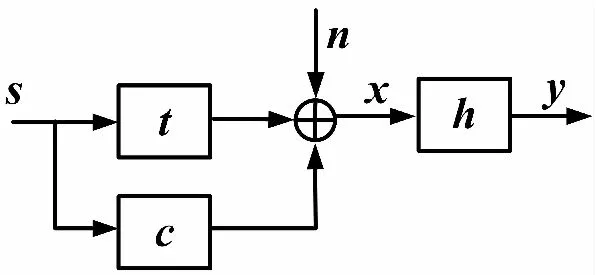
圖1 相關雜波下的信號模型
圖1中,長度為Ns的發射波形用s∈Ns×1表示;TIR和CIR分別用t∈Nt×1和c∈Nc×1表示[12];噪聲和接收機權值分別用n∈Nn×1和h∈Nh×1表示;目標和環境的回波用x表示,其長度Nx=Nh=Ns+Nt-1。信號模型可表示為
x=t*s+c*s+n=Ts+Cs+n
=St+Sc+n=st+sc+n
(1)
y=hHx
(2)


(3)
同理,矩陣S亦可表示為

(4)
文中假定噪聲向量n服從均值為0,協方差矩陣為單位陣的復高斯分布,也即n~CN(0Nn,Rn),其中,0Nn∈Nn×1的含義為Nn×1維零向量,Rn的含義為Nn×Nn維的非奇異Hermitian矩陣。如果噪聲為高斯白噪聲,則有其協方差矩陣取大于零的固定值,INn∈Nn×Nn代表Nn×Nn維單位陣);如果Rn不是單位陣,則代表Rn為高斯色噪聲。CIR可以認為是服從高斯分布的,即c~CN(0Nc,Rc),Rc代表Nc×Nc維的非奇異Hermitian矩陣。同時,假定隨機分布下TIR的目標向量t服從均值為0Nt,協方差矩陣為Rt的圓對稱復高斯分布[13],即t~CN(0Nt,Rt)。
2 波形設計方法
2.1 基于互信息方法的問題描述
從信息論的觀點出發,通過設計發射波形,使雷達回波中包含更多的目標信息,從而實現目標參數的有效估計[14]。因此,可采用目標與雷達回波之間互信息的大小作為對目標估計性能的度量,互信息越大,對目標參數的估計就越準確。本文以最大化MI為優化準則進行波形設計,目標t和回波x之間的互信息可表示為
I(x;t|S)=h(x|S)-h(x|t,S)
(5)
其中h(x|S)表示S已知時回波信號x的熵,而h(x|t,S)則表示S和t均已知時x的熵。其中,t和x服從聯合高斯分布且可表示為[15]
(6)
令Rx=SRtSH+SRcSH+Rn,x的概率密度函數可表示為
(7)
則h(x|S)和h(x|t,S)可分別表示為
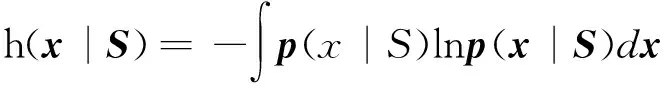
=ln det(SRtSH+SRcSH+Rn)+Nxlnπ+Nx
(8)
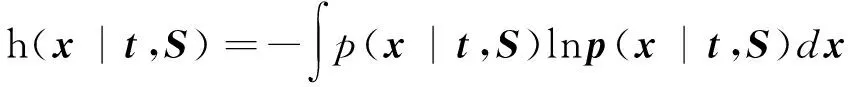
=ln det(SRcSH+Rn)+Nxlnπ+Nx
(9)
將式(8)和式(9)代入式(5),可得互信息為
I(x;t|S)=ln det[INx+SRtSH(SRcSH+Rn)-1]
(10)
可以看出,互信息是波形矩陣S的函數,可通過優化波形提高I(x;t|S),從而增強雷達的估計性能。接下來,對波形加以能量和PAR約束,并且在目標和雜波先驗知識不準確的情況下進行穩健波形設計。
2.2 低峰均比穩健波形設計
考慮到需要對波形的幅度加以PAR約束,PAR一般定義為[16]
(11)
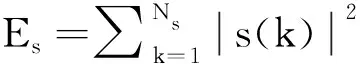
(12)
2.2.1 問題模型構建
結合式(10),同時考慮式(12)所示波形的PAR約束,則MI準則下的波形設計問題模型可表示為
(13)
其中,波形矩陣S的結構如式(4)所示。
可以看出,問題P的目標函數是非凸的,且兩個不等式約束條件是非齊次的,同時優化問題中的矩陣變量S是波形向量s經過F函數映射的Toeplitz卷積矩陣,因此該優化問題較為復雜,很難直接得到波形的解析解。
首先,為了使問題P得以求解,需對其目標函數進行轉化,應用矩陣求逆引理[18],可得
(14)
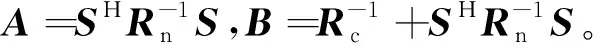
(15)
因此,PAR約束下基于極大極小化準則的穩健波形設計問題可表示為
(16)
2.2.2 不確定集下的穩健波形設計
對Rc和Rt進行特征值分解,則Rc和Rt可分別表示為[19]
Rc=UΣcUH
(17)
Rt=UΣtUH
(18)
其中Σc=diag(λc,1,…,λc,Nc),Σt=diag(λt,1,…,λt,Nt),其對角元素為Rc和Rt的特征值,同時也代表CIR和TIR功率譜密度的采樣。由于Nt=Nc,則酉矩陣U可表示為
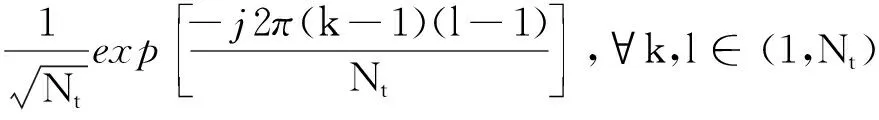
(19)
假定Rt和Rc的特征值在一定區間內波動,該波動區間與反饋信息的估計精度有關,于是不確定集可表示為
(20)
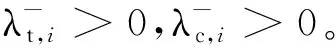
同理,高斯噪聲也可表示為
Rn=VΣnVH
(21)
其中Σn=diag(λn,1,…,λn,Nn),V為Nn×Nn維的酉矩陣,其元素可通過式(19)表示(將Nt用Nn代換)。
將式(17)、式(18)和式(21)代入式(16)所示問題中的目標函數,可得
(22)
式(22)所示極大極小化問題的目標函數是非凸的,且第二個約束條件屬于非齊次不等式約束,因此該問題是一個非凸問題[20]。
由于式(22)所示優化問題中波形與噪聲、CIR和TIR的協方差矩陣是互相獨立的,因此目標函數中的極大化和極小化的位置可互換,因此其目標函數也可轉換為
(23)
此外,當λt,i和λc,i已知時,根據Hadamard不等式[21],若要使目標函數取得極大值,波形矩陣S應滿足如式(24)結構。
(24)
其中Λs=diag(λs,1,…,λs,Nt)。將式(24)代入式(22)所示問題的目標函數,則優化問題可轉化為
(25)
可以看出,式(25)所示問題的目標函數與λc,i成反比,而與λt,i成正比,于是內部極小化問題所示目標函數可表示為
(26)
因此,優化問題可轉換為
(27)
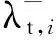
3 仿真實驗與分析
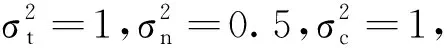
(28)
(29)
其中ui表示服從標準正態分布的隨機變量,于是不確定集變化范圍可表示為圖2所示。
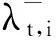
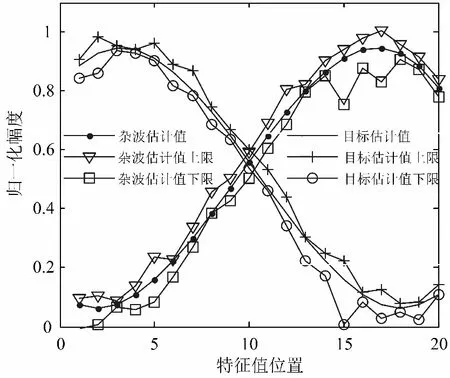
圖2 目標和雜波特性不確定集區間
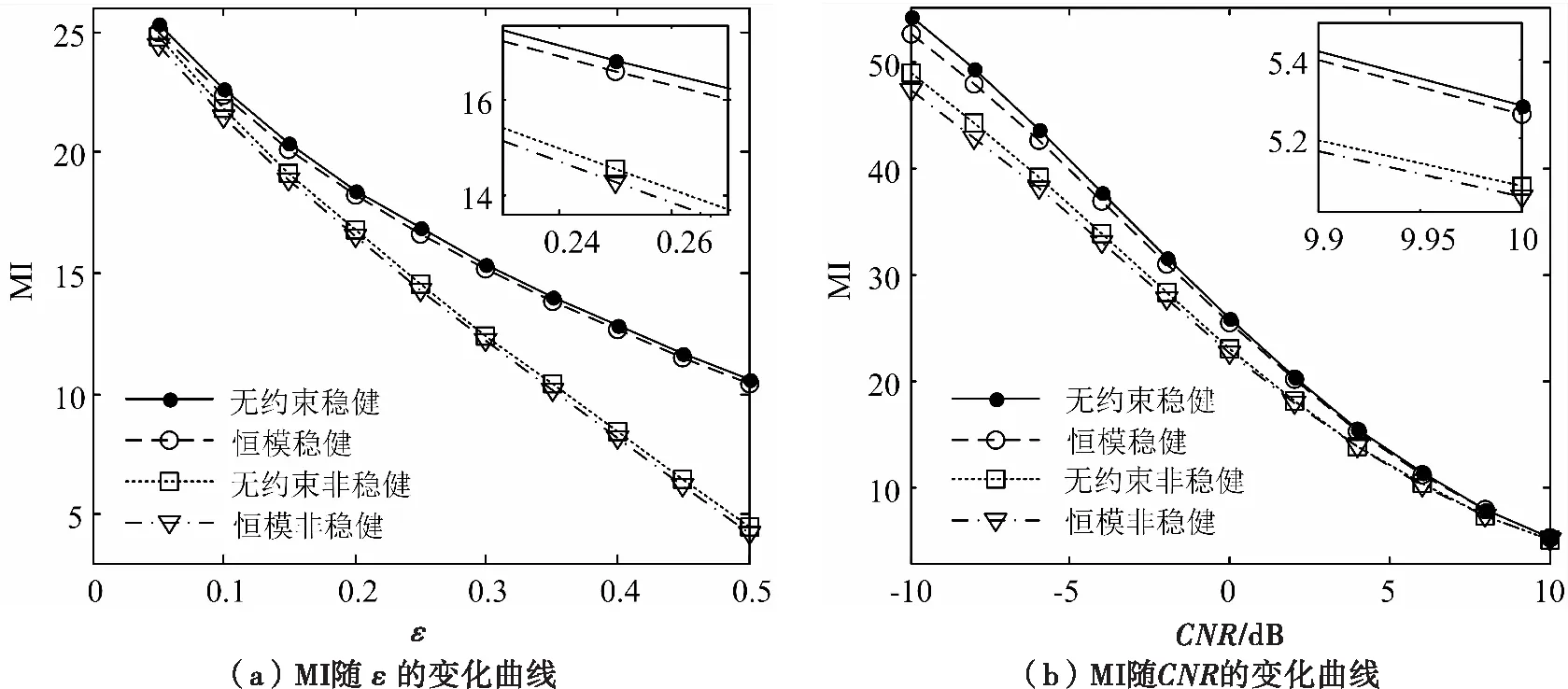
圖3 不同估計波形穩健性能對比
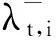
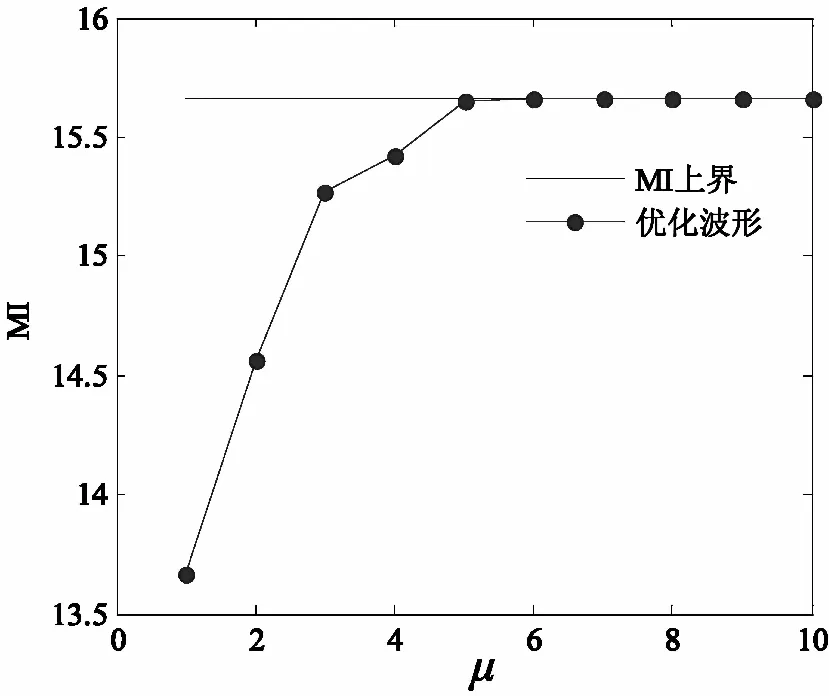
圖4 優化波形的MI隨PAR約束的變化
圖5展示的是不同PAR值下波形的實部和虛部,μ=Ns表示在只有能量約束時所求的波形,可以看出點此時分布半徑較大,也間接說明波形峰值幅度較大,發射端功率利用率低,實用性較差。而當μ=1時,此時所形成的是一個原圓,說明波形的幅度是恒定的;而當μ=2時,圓的分布半徑略大于μ=1時波形,且波形的MI高于恒模波形。從圖4和圖5可以看出,低PAR波形(例如μ=2)不僅能較好地兼顧發射機的效能(μ=2時分布半徑較小,說明峰值幅度較小),亦可以使雷達具有較好的估計性能(比恒模波形有更高的MI),說明低PAR波形實用性較強。
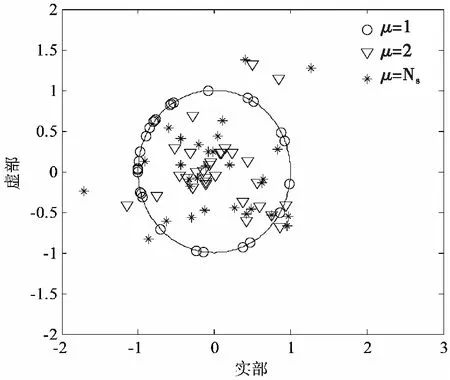
圖5 不同PAR約束下波形的實部和虛部
此外,對算法的有效性進行驗證。將優化波形與相位編碼波形和線性調頻(Linear Frequency Modulation, LFM)波形進行對比,如圖6所示,其中LFM波形可表示為[10]
(30)
圖6為不同發射能量下優化波形與常用波形的對比,從圖6可以看出,隨著發射能量增加,三種波形的MI取值逐漸增大,產生的優化波形對應的MI要優于相位編碼波形和線性調頻波形,驗證了所提方法有效性。
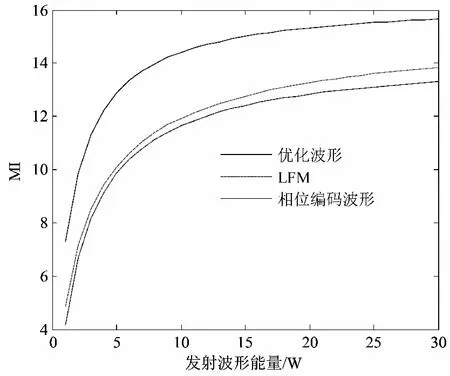
圖6 不同波形估計性能對比
4 結束語
為了提高雷達功率放大器的效能,增強波形在TIR和雜波先驗知識不準確時的穩健性能,基于極大極小化準則,研究了任意PAR約束下的認知雷達穩健波形設計問題。以CIR和TIR協方差矩陣特征值的不確定集表征CIR和TIR的波動范圍,基于極大極小化準則構建MI準則下的問題模型,在不確定集范圍內給出了MI最差情況下CIR和TIR的取值,并結合SLP方法實現了PAR約束下的穩健波形設計。仿真結果表明,與常用波形相比,優化波形具有更好估計性能,在目標和信號相關雜波不確定集范圍內,所求波形具有較好的穩健性能。

