兩等量點電荷產生的電場問題在高考試題中的創新設計及解答策略研究

路文柱 馬秋石

(江蘇省徐州市第三十六中學)

真空中兩個等量點電荷產生的電場問題是近年高考的一個熱點,在每年高考中均有涉及并不斷創新變化,創新變化主要體現在從知識立意到能力立意,從一個點電荷產生的電場,到兩個等量點電荷產生的電場相疊加,再不斷創新到多個點電荷甚至是線狀分布(帶電的線段)、面狀分布(帶電的平面)及體狀分布(帶電的曲面或幾何體)電荷電場的疊加,試題情境也從一維空間到二維空間再到三維空間,創新設計的意義在于科學設計試題情境,增強試題對“基礎性、綜合性、應用性、創新性”及獨立思考和運用所學知識分析問題、解決問題的能力考查;試題還充分體現大綱對物理觀念、科學思維,科學探究等核心素養的要求。解答此類問題的策略是熟知等量點電荷電場模型的相關結論,根據試題情境,靈活構建物理模型,利用對稱法、等效法、整體法等物理思想方法,結合電場強度和電勢的決定式定性或半定量地分析解答。雖然每年的高考題都在不斷創新,但萬變不離其宗,追蹤相關高考題的命題規律,挖掘命題者的命題意圖及創新思路有利于高中物理的復習教學。

1 單個點電荷產生的電場模型及相關結論

2 兩等量異種點電荷的電場模型及相關結論

(1)兩等量異種點電荷的電場線疏密分布關于兩點電荷連線及其連線的中垂線對稱(如圖1)。

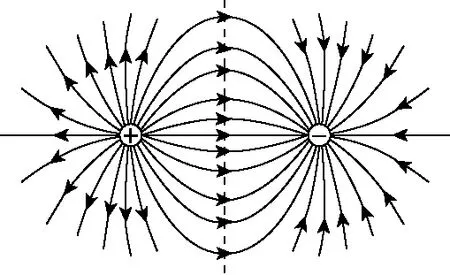
圖1

(2)兩等量異種點電荷的連線是一條從正電荷指向負電荷的電場線,沿電場線方向電勢一直減小;電場強度先變小再變大,連線中點處電場強度最小;兩電荷連線的中垂線是一條電勢為0的等勢線(取無限遠處電勢為零),靠近正點電荷一側,電勢為正,靠近負點電荷一側,電勢為負(如圖2)。

圖2

(3)關于兩點電荷連線對稱的兩點電勢相同,電場強度相等(如圖2);關于兩點電荷連線的中垂線對稱的兩點電勢相反,電場強度大小相等(平行連線分量相同,垂直連線分量相反);關于連線中點對稱的兩點電場強度相等,電勢相反(如圖3)。

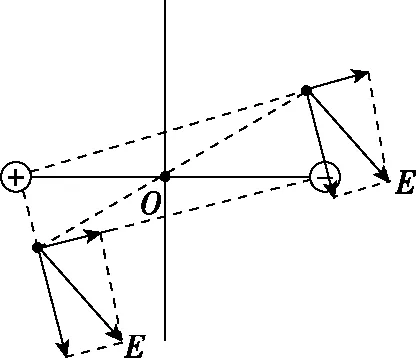
圖3

3 兩等量同種點電荷的電場模型及相關結論

(1)兩等量同種正點電荷的電場線疏密分布關于兩點電荷連線及其連線的中垂線對稱(如圖4)。

圖4

(2)沿兩等量同種正點電荷連線從點電荷向連線中點,電勢一直減小;電場強度也一直減小,中點處電場強度最小(為0);沿兩電荷連線的中垂線,連線中點向無限遠處電勢一直減小,電場強度先增大后減小(如圖5)。

圖5

(3)關于兩點電荷連線對稱的兩點電勢相同,電場強度大小相等(平行連線分量相反,垂直連線分量相同);關于兩點電荷連線的中垂線對稱的兩點電勢相同,電場強度大小相等(平行連線分量相反,垂直連線分量相同)。關于連線中點對稱的兩點電場強度大小相等、方向相反,電勢相同(如圖6)。

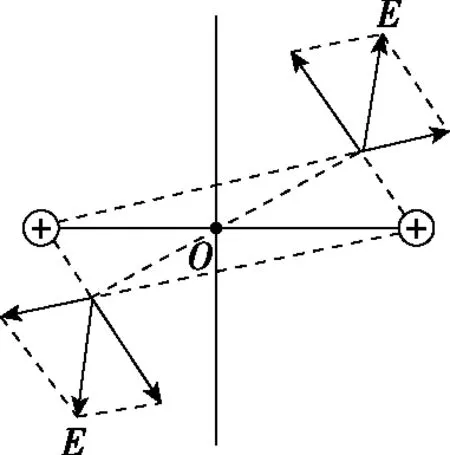
圖6

4 近年高考試題中的創新設計例析

近年相關高考試題以物理教材兩等量點電荷電場線分布為母版,將一組或多組等量點電荷的電場進行組合,變換試題情景,或是只有一組點電荷(2020·7月浙江卷·8),或是多組點電荷成線狀分布(2020·全國卷Ⅱ·20)、面狀分布(2022·全國乙卷·19)、體狀分布(2019·全國卷Ⅲ·21),或先線狀再體狀分布(2022·湖南卷·2)等。試題設計意圖是為了體現對所考查知識的“基礎性、綜合性、應用性、創新性”要求,從能力立意出發,以甄別有“學力”的考生,起到選拔人才的目的和引導教學的導向作用。下面以近年高考試題為例分析、展望兩等量點電荷電場的命題創新及趨勢。

高考創新一:將兩點電荷的電場線圖變為等勢線圖,比較不同位置的場強、電勢及電勢能大小。

【例1】(2020·7月浙江卷·8)空間P、Q兩點處固定電荷量絕對值相等的點電荷,其中Q點處為正電荷,P、Q兩點附近電場的等勢線分布如圖7所示,a、b、c、d、e為電場中的5個點,設無窮遠處電勢為0,則

圖7

( )

A.e點的電勢大于0

B.a點和b點的電場強度相同

C.b點的電勢低于d點的電勢

D.負電荷從a點移動到c點時電勢能增加

【答案】D

【點評】本題是一個最基本的等量異種點電荷模型,只是將教材上的電場線圖變為等勢線圖,可利用點電荷場強和電勢的決定式以及疊加原理快速解答。

高考創新二:變換兩點電荷的試題情境,使其處于立體圖上的兩特殊位置,比較其他特殊位置的場強、電勢及電勢能大小。

【例2】(2019·全國卷Ⅲ·21)(多選)如圖8,電荷量分別為q和-q(q>0)的點電荷固定在正方體的兩個頂點上,a、b是正方體的另外兩個頂點,則

圖8

( )

A.a點和b點的電勢相等

B.a點和b點的電場強度大小相等

C.a點和b點的電場強度方向相同

D.將負電荷從a點移到b點,電勢能增加

【答案】BC

【點評】本試題情境是一個正方體的對角線上兩點電荷產生的電場問題,表面上看是兩等量異種電荷產生的電場在三維空間中的問題,對學生解題有一定干擾,無疑增加了學生心理壓力,但仔細觀察就會發現,其實還是關于兩等量異種電荷連線中點對稱點的問題,利用前述結論即可正確判斷。

高考創新三:讓兩組或多組等量點電荷呈對稱分布于平面或立體空間,比較一些對稱點或特殊點的場強、電勢近而判斷兩點間電場力做功正負及電勢能大小。

【例3】(2022·全國乙卷·19)(多選)如圖9,兩對等量異號點電荷+q、-q(q>0)固定于正方形的4個頂點上。L、N是該正方形兩條對角線與其內切圓的交點,O為內切圓的圓心,M為切點。則

圖9

( )

A.L和N兩點處的電場方向相互垂直

B.M點的電場方向平行于該點處的切線,方向向左

C.將一帶正電的點電荷從M點移動到O點,電場力做正功

D.將一帶正電的點電荷從L點移動到N點,電場力做功為零

【答案】AB

【點評】本題情境是分布在正方形四個頂點上的兩組等量電荷,對角線上對稱的兩點以及一個邊上的點跟正方形的幾何中心的電場進行比較,物理情境設置較為新穎,一個題同時考查兩組等量同種電荷或等量異種電荷電場的分布及疊加,對電場相關物理核心知識均做了深入考查,體現了以知識立意向能力立意的轉變。本題對那些死記硬背,缺乏靈活應變及分析解決問題能力的同學是不友好的。要準確高效解答本題,不僅要掌握好點電荷電場強度和電勢的概念及其計算公式等基本知識和基本技能,還要能靈活將幾個點電荷分類及組合,熟知電場強度及電勢疊加的運算法則。一道題對“理解能力” “推理能力” “分析綜合能力” “應用數學處理物理問題的能力”均有考查,起到了服務選才、引導教學的導向作用。

高考創新四:讓多組等量電荷呈對稱的線狀分布,比較空間一些對稱點或相似點的場強、電勢。

【例4】(2020·全國卷Ⅱ·20)(多選)如圖10,豎直面內一絕緣細圓環的上、下半圓分別均勻分布著等量異種電荷。a、b為圓環水平直徑上的兩個點,c、d為豎直直徑上的兩個點,它們與圓心的距離均相等。則

圖10

( )

A.a、b兩點的場強相等

B.a、b兩點的電勢相等

C.c、d兩點的場強相等

D.c、d兩點的電勢相等

【答案】ABC

【點評】本題創造性地將多組等量異種電荷分布在一豎直面內絕緣細圓環的上、下兩個半圓上,使其呈線狀分布,立意新穎,對物理觀念以及物理思維和方法如等效法、對稱法、整體法等均有考查,對學生能力要求較高。將點電荷分組并結合等量點電荷電場模型的結論可準確解答。

高考創新五:讓多組等量電荷呈對稱的線狀分布,再組合為體狀分布,求特殊點的場強、電勢。

【例5】(2022·湖南卷·2)如圖11,四根完全相同的均勻帶正電絕緣長棒對稱放置在長方體的四條長邊a、b、c、d上。移去a處的絕緣棒,假定另外三根絕緣棒電荷分布不變。關于長方體幾何中心O點處電場強度方向和電勢的變化,下列說法正確的是

圖11

( )

A.電場強度方向垂直指向a,電勢減小

B.電場強度方向垂直指向c,電勢減小

C.電場強度方向垂直指向a,電勢增大

D.電場強度方向垂直指向c,電勢增大

【答案】A

【點評】本題以四根完全相同的均勻帶正電絕緣長棒對稱放置在長方體的四條長邊上,構成了三維空間的物理情境,且每根長棒所帶電荷呈線狀分布,由于學生只學過點電荷電場的電勢和電場強度的計算公式,對線狀分布的電荷感覺無從下手,顯然只學會基本知識和基本技能是很難完成此題的解答。此題著重考查學生的物理觀念和分析解決問題的能力。

5 今后高考試題中的創新設計思考

【自編創新變式題1】如圖12所示,兩等量同種點電荷+Q產生的電場中,A、O是兩點電荷連線上的點且O為連線的中點,B、C是兩點電荷連線的垂直平分線上關于O點對稱的兩點。將一個負點電荷在外力作用下先沿AB從A移到B,再沿BC從B移到C,則下列說法中正確的是

圖12

( )

A.從A移到B,負點電荷的電勢能一定減小

B.從B移到C的過程中負點電荷所受的靜電力先做正功后做負功

C.負點電荷在A點所受靜電力一定大于B點所受靜電力

D.負點電荷從B移到O的過程中靜電力一定先變大后變小

【解析】由前文結論可知A點電勢高于O點電勢,O點電勢高于B點電勢且為正值,即φA>φO>φB>0,由電勢能公式Ep=qφ知,負點電荷從A移到B,其電勢能一定增大,故A錯誤;負點電荷從B移到C的過程中所受靜電力方向先由B指向O后由C指向O,故靜電力先做正功后做負功,故B正確;根據題目所給條件,A、B兩點的電場強度大小無法比較,故C錯誤;由于沿OB及OC所在射線方向電場強度先增大后減小,但電場強度最大的點與B、C點的位置無法確定,故D錯誤。

【答案】B

【創新意圖】此題以兩等量同號點電荷的電場為背景,考查它們連線及其連線的中垂線上相關物理量關系的判斷。

【自編創新變式題2】正方形ABCD四個頂點上放置著電荷量相同的、電性如圖13所示的點電荷,O為正方形兩對角線的交點,M、N、P、Q分別為AO、BO、CO、DO的中點。取無窮遠處電勢為零,下列說法正確的是

圖13

( )

A.M、N、P、Q四點的電場強度相同

B.M、N、P、Q四點的電勢均為零

C.將一質子從M點沿MON移動到N點的過程中,電場力先做正功再做負功

D.將一電子從M點沿MOP移動到P點的過程中,其電勢能先增加后減小

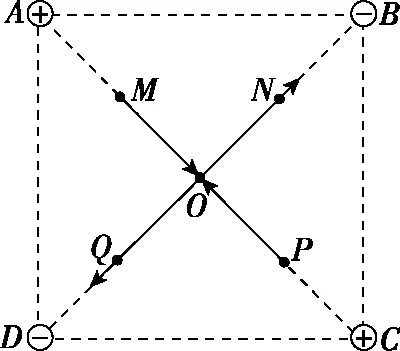
圖14

【答案】D

【創新意圖】此題以兩組等量同號點電荷的電場為背景,考查它們連線及其連線的中垂線上相關物理量關系的判斷。

【自編創新變式題3】(多選)如圖15所示,橫截面位于豎直面內的一半球面的上、下兩半部分均勻分布著等量正負電荷。a、b為球面水平直徑上的兩個點,c、d為豎直直徑上的兩個點,它們與球心的距離均相等。則

圖15

( )

A.a、b兩點的電場強度大小相等,方向相同

B.c、d兩點的電場強度大小相等,方向不相同

C.a、b兩點的電勢相等

D.c、d兩點的電勢相等

【解析】此電場可以看成是關于水平面對稱的一對一對的上、下兩等量異種點電荷的電場的疊加,a、b兩點是每對電荷連線的中垂面上的點,場強疊加后大小不相等,方向相同;c、d兩點場強大小相等、方向不同,故A錯誤,B正確;取無限遠處電勢為0,則每一對等量異種點電荷連線的中垂面是電勢為0的等勢面,故a、b兩點的電勢相等,c點的電勢為正,d點的電勢為負,故C正確,D錯誤。

【答案】BC

【創新意圖】此題以半球面上面電荷分布的電場為背景,考查點電荷電場疊加后相關物理量的判斷及學生綜合分析問題的能力。