源于教材 提煉模型 靈活應(yīng)用
——平面向量極化恒等式及應(yīng)用探究

謝亞強(qiáng)

(甘肅省鎮(zhèn)原縣孟壩中學(xué))

在高考考查平面向量的試題中,數(shù)量積問(wèn)題有著舉足輕重的地位,一直都是高考命題的重點(diǎn)和熱點(diǎn).求解平面向量數(shù)量積問(wèn)題的常規(guī)解題思路:一是依據(jù)長(zhǎng)度和夾角(定義),二是利用坐標(biāo)運(yùn)算.而對(duì)于一些具有中點(diǎn)或能夠構(gòu)造中點(diǎn)的向量的數(shù)量積問(wèn)題,應(yīng)用平面向量的“極化恒等式”求解,則可以縮短思維線路,減少運(yùn)算量,尤其是對(duì)于一些數(shù)量積的客觀試題可謂是“秒殺”!“極化恒等式”是源于教材中的一道練習(xí)題,本文就從這道練習(xí)題說(shuō)起,提煉平面向量的“極化恒等式”的兩種模型,并通過(guò)有關(guān)高考題中的“常規(guī)解法”與“極化恒等式”解法的比較,體會(huì)“極化恒等式”解題的靈活性和解法的優(yōu)越性.

一、課本題目

2019版普通高中教科書(shū)A版數(shù)學(xué)必修第二冊(cè)第22頁(yè)練習(xí)3.求證:(a+b)2-(a-b)2=4a·b.

證明:因?yàn)?a+b)2=a2+2a·b+b2①,

同理:(a-b)2=a2-2a·b+b2②.

所以①-②得(a+b)2-(a-b)2=4a·b.

二、極化恒等式及其幾何模型

1.極化恒等式

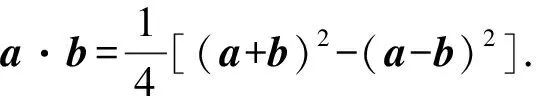
我們稱這一公式為平面向量的“極化恒等式”,它建立起兩向量的數(shù)量積與兩向量的和、兩向量的差三者之間的等量關(guān)系,可以“知二求一”.

平面向量的“極化恒等式”是用來(lái)解決起點(diǎn)相同的數(shù)量積問(wèn)題,分為三角形模型與平行四邊形模型.

2.極化恒等式三角形模型

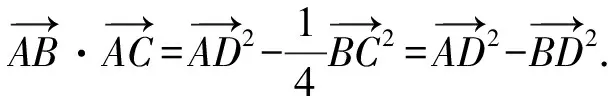
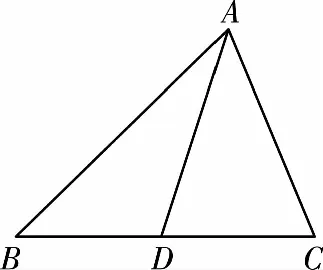
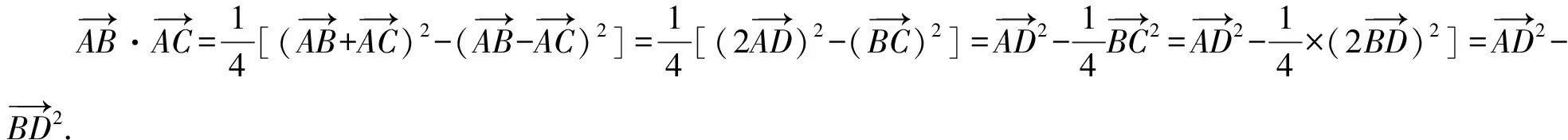
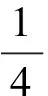
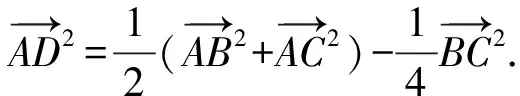
3.極化恒等式平行四邊形模型

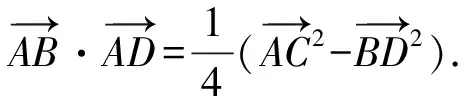
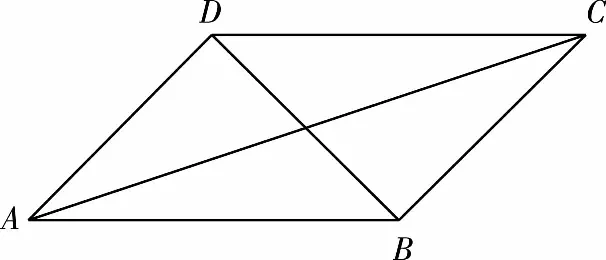
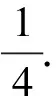
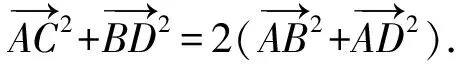
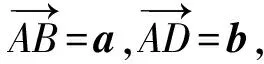
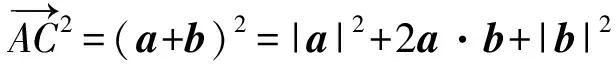
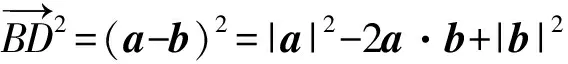
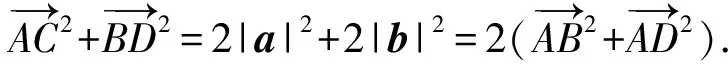
三、極化恒等式的應(yīng)用

極化恒等式是將兩個(gè)非零向量的數(shù)量積轉(zhuǎn)化為這兩個(gè)向量的“和向量”與“差向量”,所以當(dāng)兩個(gè)向量的“和向量”與“差向量”均為已知向量時(shí),可以考慮應(yīng)用極化恒等式進(jìn)行轉(zhuǎn)化.特別是在求解有中點(diǎn)或能夠構(gòu)造中點(diǎn)的向量的數(shù)量積問(wèn)題時(shí),極化恒等式有著很好的應(yīng)用.下面以三道高考題為例,通過(guò)應(yīng)用常規(guī)解法與應(yīng)用極化恒等式的解法比較,來(lái)說(shuō)明極化恒等式在求解有關(guān)平面向量數(shù)量積客觀性問(wèn)題的優(yōu)越性.

( )

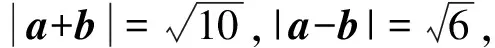
A.1 B.2 C.3 D.5

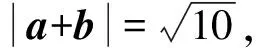
所以(a+b)2=a2+2a·b+b2=10 ①,

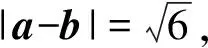
所以(a-b)2=a2-2a·b+b2=6 ②,

所以①-②得4a·b=4,所以a·b=1,

故選A.

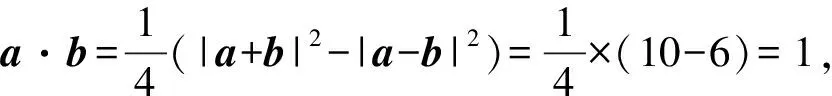
點(diǎn)評(píng):常規(guī)解法相當(dāng)于推導(dǎo)了一次“極化恒等式”后求解,而后者直接利用“極化恒等式”結(jié)論代入解答,可謂快速、簡(jiǎn)捷、“秒殺”.

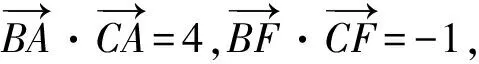
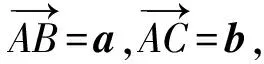
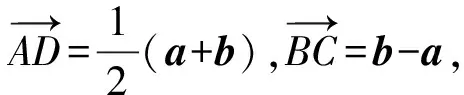
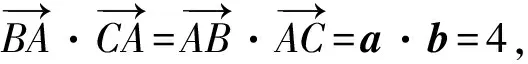
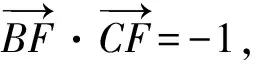
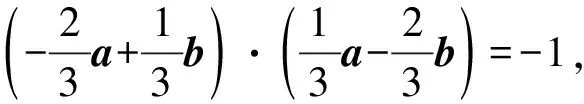
展開(kāi)整理得-2(a2+b2)+5a·b=-9,

所以-2(a2+b2)+5×4=-9,

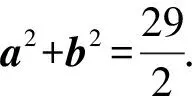
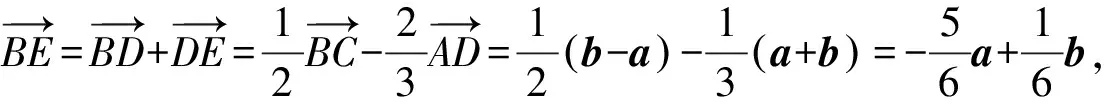
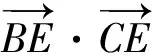
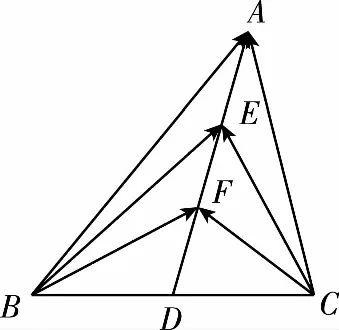
常規(guī)解法2.(坐標(biāo)法)如圖,以BC所在直線為x軸,D為坐標(biāo)原點(diǎn),建立平面直角坐標(biāo)系xDy.

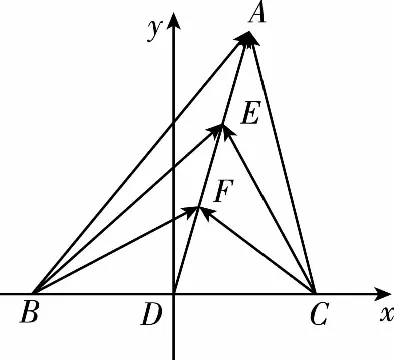
設(shè)B(-a,0),A(b,c),

因?yàn)镈為BC的中點(diǎn),所以C(a,0).

又因?yàn)镋,F是AD上的兩個(gè)三等分點(diǎn),

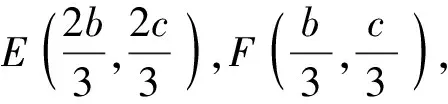
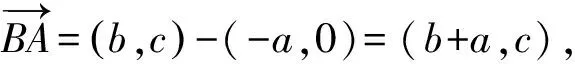
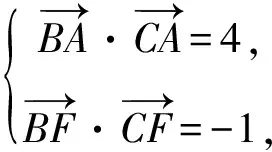
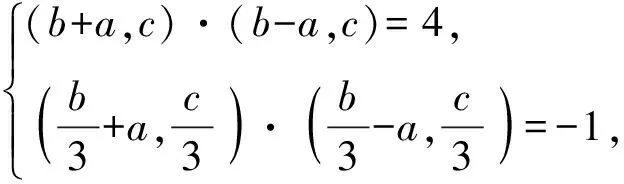
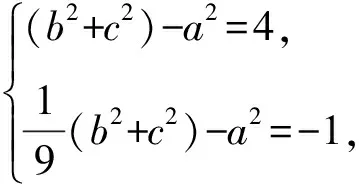
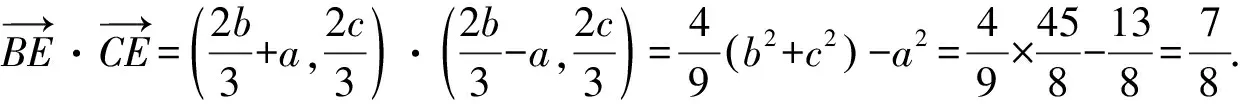
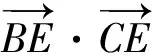
“極化恒等式”解法:因?yàn)镈是BC的中點(diǎn),所以由極化恒等式,

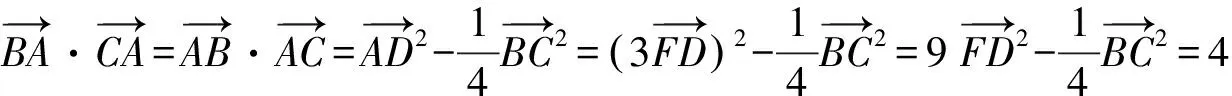
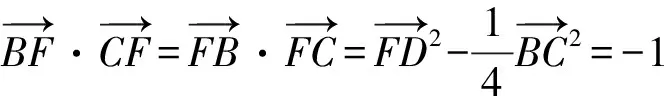
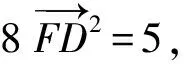
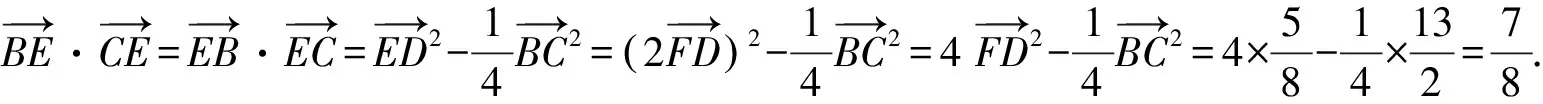
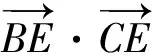
點(diǎn)評(píng):兩種常規(guī)解法無(wú)論是基底法還是坐標(biāo)法,過(guò)程冗繁、復(fù)雜,計(jì)算量大,令人眼花繚亂,稍有不慎極易出錯(cuò).而“極化恒等式”解法依據(jù)D是BC的中點(diǎn),利用“極化恒等式”轉(zhuǎn)化求解,則簡(jiǎn)捷、從容.常規(guī)解法與“極化恒等式”解法比較,孰繁孰簡(jiǎn)、一目了然,足以體現(xiàn)出“極化恒等式”的明顯優(yōu)勢(shì).

( )

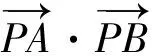
A.[-5,3] B.[-3,5]

C.[-6,4] D.[-4,6]

常規(guī)解法1.(坐標(biāo)+三角)依題意建立如圖所示的平面直角坐標(biāo)系,則C(0,0),A(3,0),B(0,4),

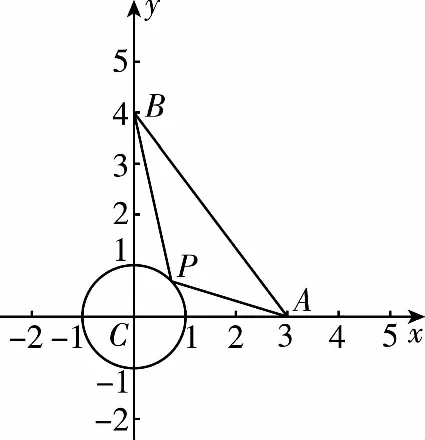
因?yàn)镻C=1,所以P是以C為圓心,1為半徑的圓上的動(dòng)點(diǎn),

設(shè)P(cosθ,sinθ),θ∈[0,2π],

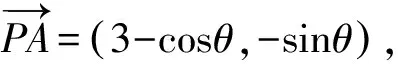
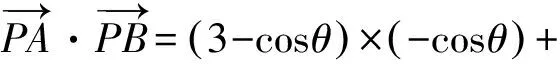
因?yàn)?1≤sin(θ+φ)≤1,

所以-4≤1-5sin(θ+φ)≤6,

常規(guī)解法2.(向量分解+三角)

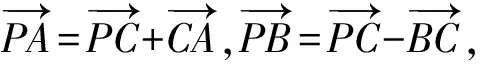
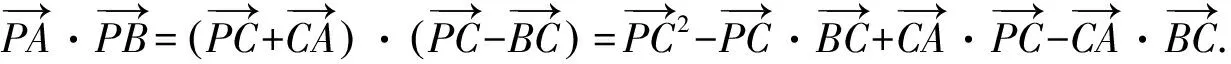
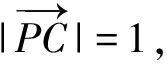
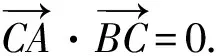
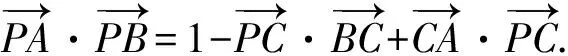
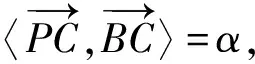
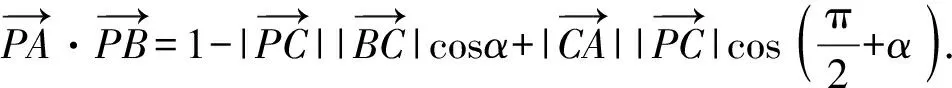
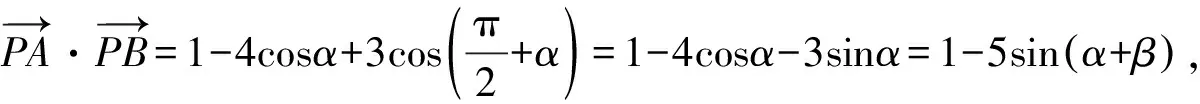
因?yàn)?1≤sin(α+β)≤1,

所以-4≤1-5sin(α+β)≤6,

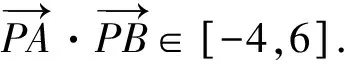
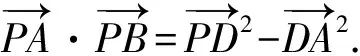
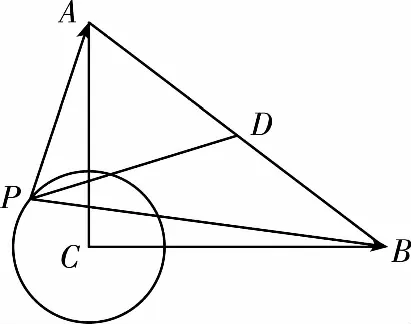
因?yàn)樵赗t△ABC中,AC=3,BC=4,

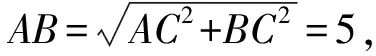
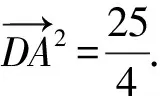
因?yàn)镻C=1,所以P是以C為圓心,1為半徑的圓上的動(dòng)點(diǎn),

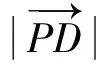
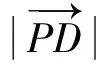
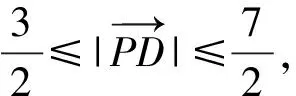
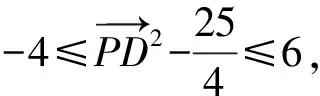
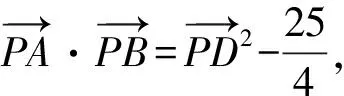
四、結(jié)語(yǔ)