素養導向下的習題探究
——以解析幾何中的“三定”問題為例
劉祥云 黃小燕
(江蘇省興化中學)
數學習題的探究活動不僅能夠幫助學生更好地掌握知識技能,更能幫助學生學會數學思考和實踐,是學生形成和發展數學學科核心素養的有效載體.事實上,習題對于學生而言,已經成為了掌握知識,提升能力的唯一途徑.習題做錯了匆匆地訂正一下,就急著去做下一個習題,在一次次的作業和糾錯中逐漸喪失了學習興趣與動力.展開習題的探究活動,是提升學生高階思維和學習能力的重要手段,所以在平時的教學過程中,教師要引領學生對習題進行深度思考和探究,讓學生真正地學會學數學.
1.探究解法,追求自然

【解析】設直線l的方程為x=my+2,點M(x1,y1),N(x2,y2),
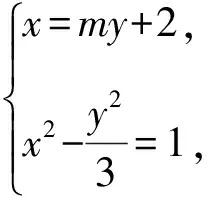
消x整理得(3m2-1)y2+12my+9=0,
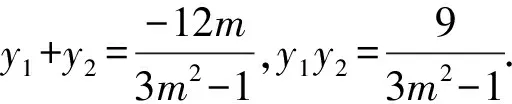
由題可得F(2,0),A1(-1,0),A2(1,0),

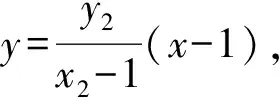
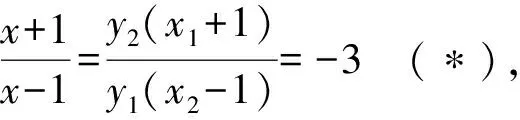
對于(*)式的化簡,有以下三種方法:
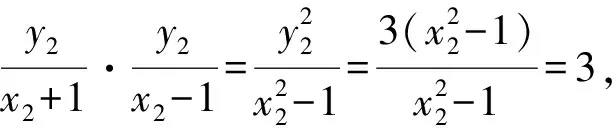
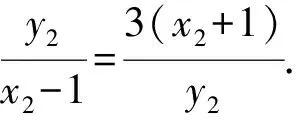
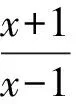
=-3.
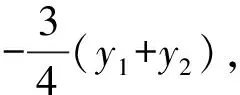
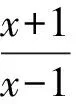
=-3.
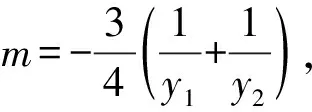
【評注】本題是我校一次平常測試中的試題,位于試卷的最后一題,得分率較低.本題中直接影響計算的難易程度就是(*)式的轉化路徑,方法一是利用韋達定理,把根與系數的關系不對稱形式,轉化為對稱形式,方法二是想實現和與積之間的轉化,所以由韋達定理提煉出和與積之間的關系,將積轉化為和,得到定值,方法三想把變量m表示出來,再進行代換,從而得到定值,三種解法算理清晰,目標明確,每種轉化方法都來自于自然想法,合情合理.
2.探究背景,把握本質
為了探究問題的背景,將題目中的雙曲線一般化,通過計算發現定直線即為右準線,得到命題1.
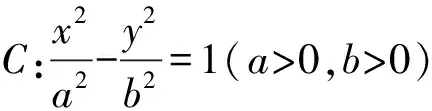
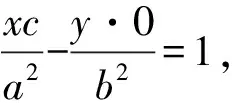
在高觀點下探尋數學本質,有一覽眾山小的感覺,此時又有意猶未盡的感覺,根據極線與極點的知識,將雙曲線推廣到有心圓錐曲線,很容易的發現下面兩個命題(命題2與命題1的極線證明類似,不再贅述).
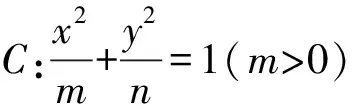
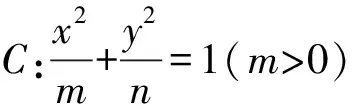
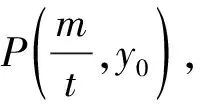
3.探究定值,提升“四能”
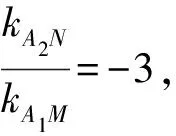
【證明】設直線l的方程為x=my+c,點M(x1,y1),N(x2,y2),
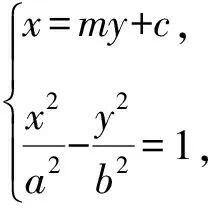
得(m2b2-a2)y2+2b2cmy+b4=0,
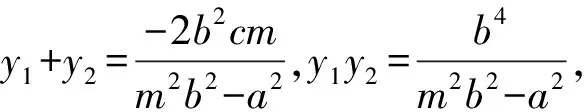
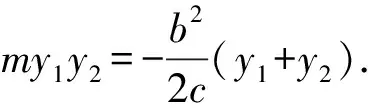
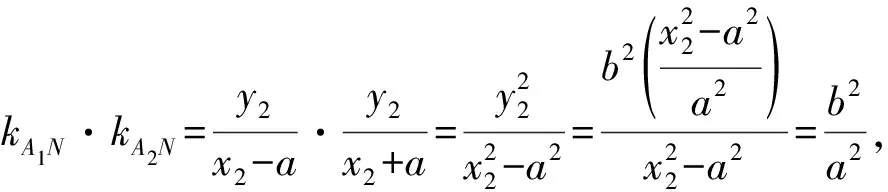
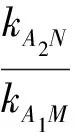
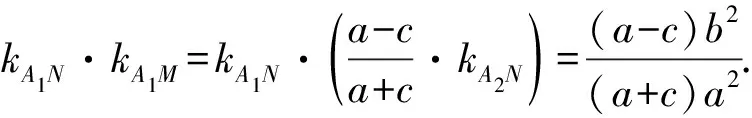
因此,在同一道習題中,同時探究生成了定直線、定點、定值問題,但上面的證法不利于將該性質在圓錐曲線中進行推廣,故根據兩個斜率之積聯想到兩根之積,可以構造“齊次式”方程,用韋達定理來證明.
【另證】設直線l的方程為x=my+c,點M(x1,y1),N(x2,y2),
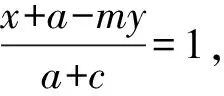
雙曲線方程可變為b2(x+a)2-a2y2-2ab2(x+a)=0,
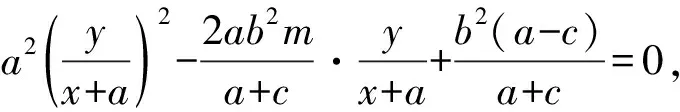
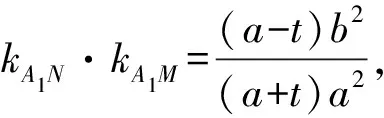
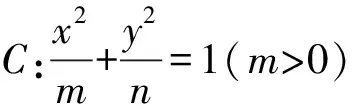
4.探究應用,破舊立新
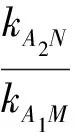
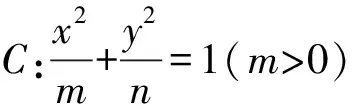
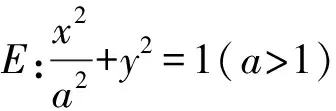
(1)求E的方程;
(2)證明:直線CD過定點.
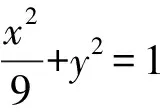
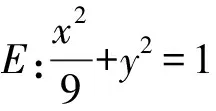
解析幾何的兩大作用是建立曲線方程和利用曲線方程研究幾何性質,而這兩個作用都對數學運算提出了很高的要求,曲線中的定點、定直線、定值三個問題也成為了解析幾何中經典的“三定”問題,新課程標準中核心素養學業水平二要求針對計算問題,要合理選擇計算方法,設計運算程序,運算求解.其中合理選擇計算方法的目的就是減少運算量,提高運算的正確率,這與高考中所提倡的“多考一點思考,少考一點運算”是相一致的.提升運算能力并不是通過試題簡單的堆積,要經過數學探究活動發揮出每道試題的最大效用,在每道試題的探究中不斷提升自己的探究能力和運算水平,逐漸學會學數學的方法,提升自身的核心素養.

