順應“三新”趨勢 探索變式教學模式
——數學變式征集活動解析幾何專題試題選登

(作者單位 姓名：甘肅省嘉峪關市第二中學 彭長軍)

(作者單位 姓名：吉林省磐石市第二中學 韓兆峰)

(作者單位 姓名：河北省定州中學 趙偉娜)

【精選變式題組】

( )

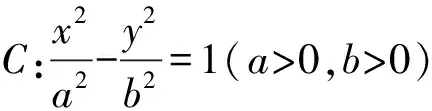
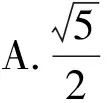
【變式1】(知識變式)將夾角變為直角

( )

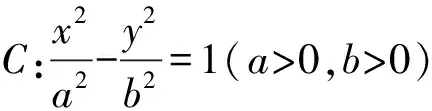
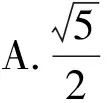
【變式2】(方法變式)將條件變為已知三角形F1NF2的面積

( )

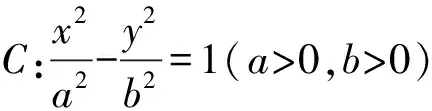
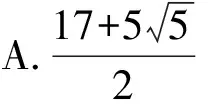
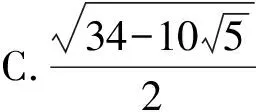
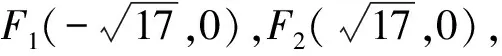
(Ⅰ)求C的方程;

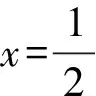
【變式1】(知識變式)由雙曲線背景到橢圓背景的變式

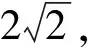
(Ⅰ)寫出C的方程;

(Ⅱ)設過點F2且斜率為k(k≠0)的直線l與曲線C交于不同的兩點M,N,點P在y軸上,且|PM|=|PN|,求點P縱坐標的取值范圍.

【變式2】(方法變式)由斜率關系探究是否存在滿足條件的點

(改編)已知動圓與圓F1:(x+5)2+y2=49和圓F2:(x-5)2+y2=1都外切.

(Ⅰ)證明動圓圓心M的軌跡C是雙曲線的一支,并求其方程;

(Ⅱ)若直線AB與軌跡C交于A,B兩點,Q(3,0),記直線AQ和BQ的斜率分別為k1,k2,且3k1k2+16=0,QP⊥AB于點P.證明:存在點N,使得|NP|為定值.

【變式3】(綜合變式)對定直線及面積的最值的探究

(Ⅰ)求Γ的方程;

(Ⅱ)若AM⊥x軸于點M,BN⊥x軸于點N,直線AN與BM交于點C.

(ⅰ)求證:點C在一條定直線上,并求此定直線;

(ⅱ)求△ABC面積的最大值.

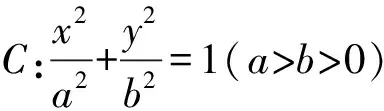
(Ⅰ)求橢圓的方程;

(Ⅱ)求四邊形ABCD面積的最小值.

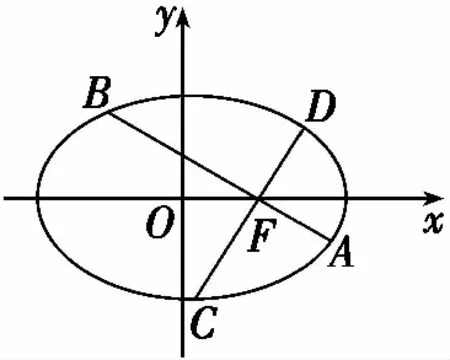
【變式1】(知識變式)曲線方程的變化:橢圓變為雙曲線

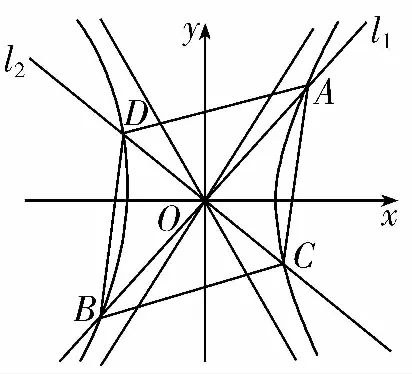
(Ⅰ)求雙曲線Γ的方程;

(Ⅱ)如圖,過原點O作互相垂直的直線l1,l2分別交雙曲線于A,B兩點和C,D兩點,A,D在x軸同側,求四邊形ABCD的面積的取值范圍.

【變式2】(方法變式)兩弦位置關系的變化:垂直變為斜率之積為定值

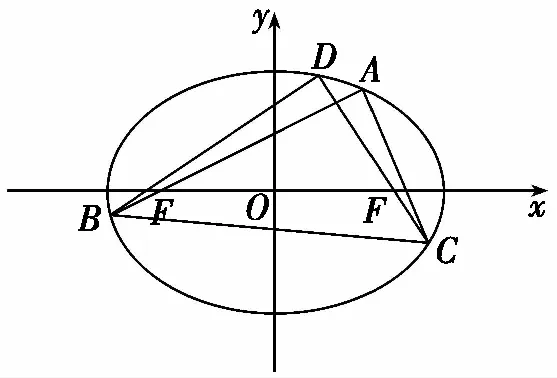
(Ⅰ)求|AB|(用k表示);

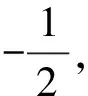
【變式3】(綜合變式)結論發生變化,求解梯形面積后利用導數研究復雜形式的最值

(Ⅰ)求橢圓C的標準方程;

(Ⅱ)過點F且斜率不為零的直線與橢圓C相交于A,B兩點,過點A,B分別作直線x=4的垂線,垂足分別為點D,E,求四邊形ABED面積的最大值.

【母題詳解及答案】

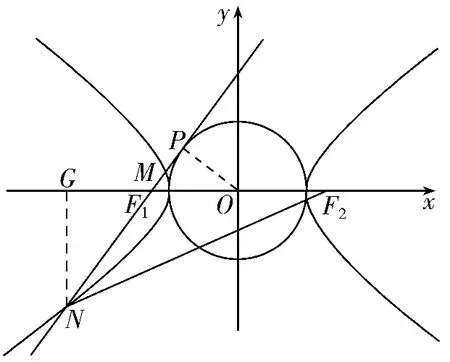
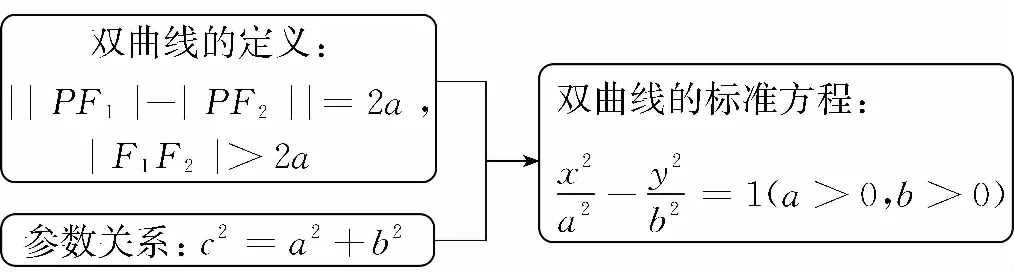
【母題1】【解題策略】充分利用已知條件通過幾何作圖、垂直輔助、巧用三角、定義搭橋等手段進行求解,相應解題步驟的思維導圖如下:

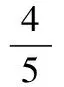
【解題思路】當M,N兩點分別在雙曲線C的左、右兩支上時,

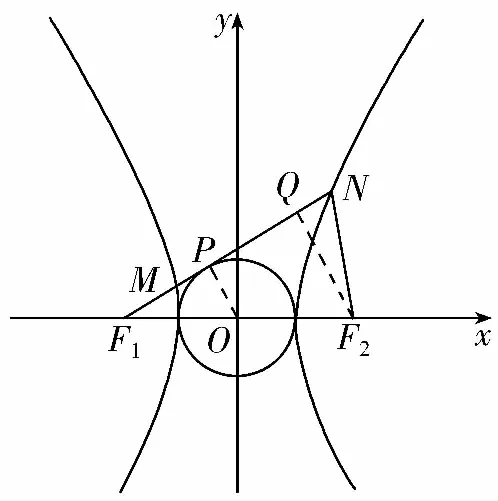
解法一:如圖,在△NF1F2中,

由余弦定理及雙曲線的定義,

得|F1F2|2=|NF1|2+|NF2|2-2|NF1||NF2|·cos∠F1NF2,

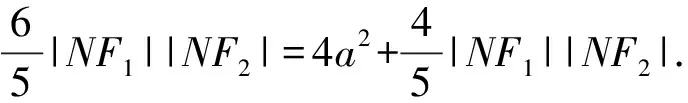
設直線MN與圓O的切點為點P,連接OP,

過點N作NG⊥x軸于點G,

易證Rt△F1PO∽Rt△F1GN,

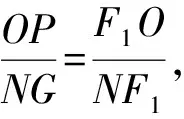
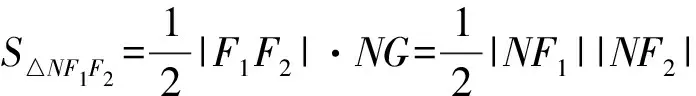
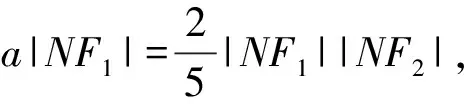
又|NF1|-|NF2|=2a,

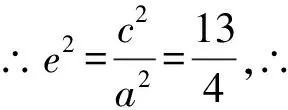
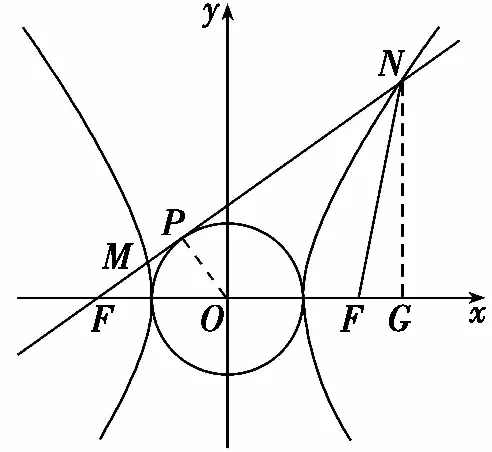
解法二:如圖,設直線MN與圓D的切點為P,連接OP,

則OP⊥MN.

過點F2作F2Q⊥F1N于點Q,

則OP∥F2Q.

又O是F1F2的中點,

∴|F2Q|=2|OP|=2a.

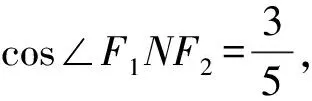
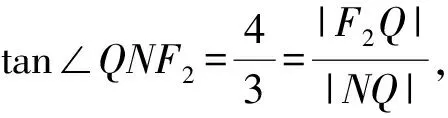
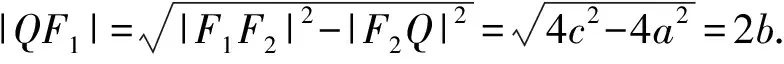
由雙曲線的定義,

得|NQ|+|QF1|-|NF2|=2a,

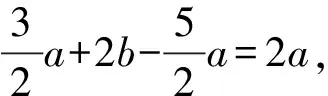
∴3a=2b,∴9a2=4b2=4c2-4a2,

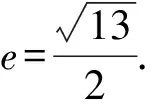
當M,N兩點均在雙曲線的左支上時,

如圖,在△NF1F2中,

由余弦定理及雙曲線的定義,

設直線MN與圓O的切點為點P,

連接OP,過點N作NG⊥x軸于點G,

易證Rt△F1PO∽Rt△F1GN,

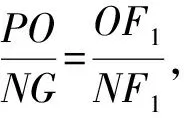
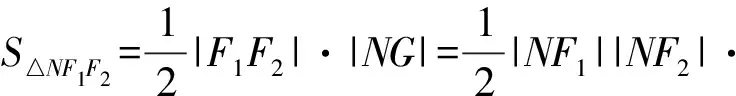
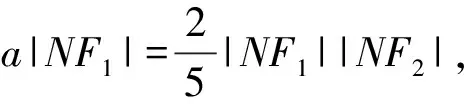
又|NF2|-|NF1|=2a,

∴4c2=4a2+a2=5a2,

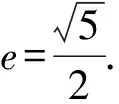
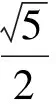
故選AC.

【變式1】C

【變式2】C

(作者單位 姓名：甘肅省嘉峪關市第二中學 彭長軍)

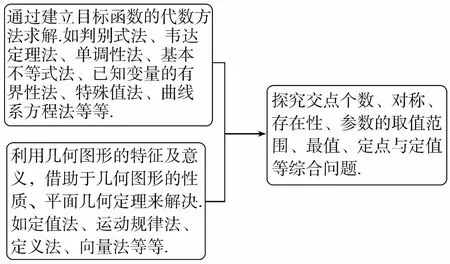
【母題2】【解題策略】(Ⅰ)由雙曲線的離心率及參數關系,根據曲線上的點滿足曲線方程,列方程(組),利用待定系數法即可解答;(Ⅱ)解法一:將直線方程與二次曲線的方程聯立,結合韋達定理處理圓錐曲線問題是最經典的方法,體現了解析幾何的特征,是該題的解題通法,也是最優解法;解法二:參數方程的使用充分利用了參數的幾何意義,要求解題過程中對參數有深刻的理解,并能夠靈活的應用到題目中;解法三:圓冪定理的應用更多的提現了幾何的思想,二次曲線系的應用使得計算更為簡單.

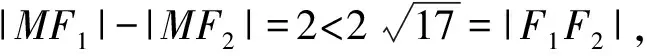
所以軌跡C是以點F1,F2為左、右焦點的雙曲線的右支,

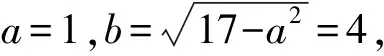
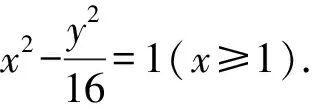
(Ⅱ)解法一:點撥:直線方程與雙曲線方程聯立

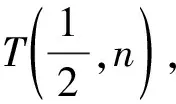
由題意可知直線AB,PQ的斜率均存在且不為0,

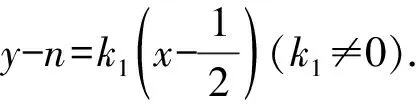
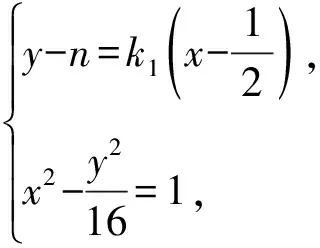
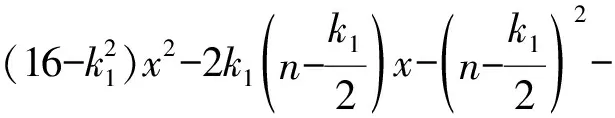
設A(xA,yA),B(xB,yB),

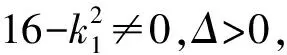
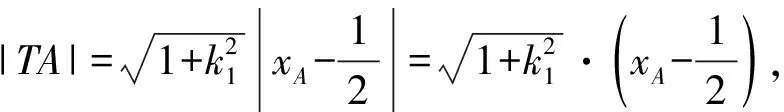
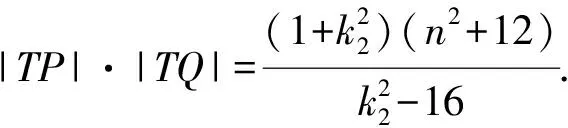
因為|TA|·|TB|=|TP|·|TQ|,

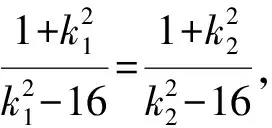
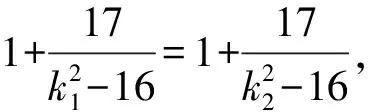
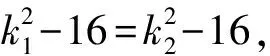
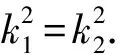
因為k1≠k2,所以k1+k2=0.

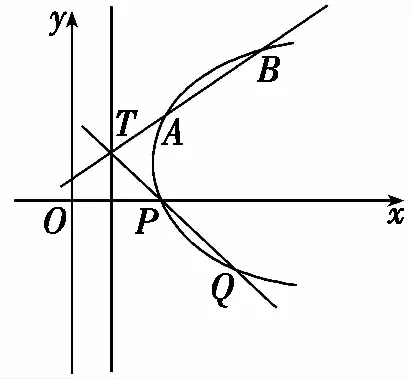
解法二:點撥:參數方程法

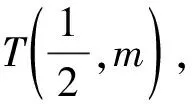
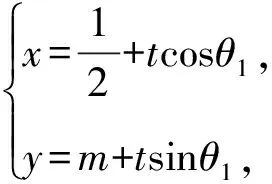
代入曲線C的方程16x2-y2-16=0(x≥1),

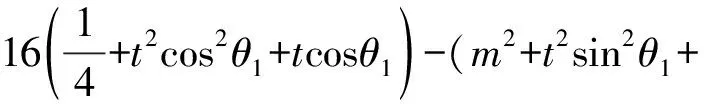
整理得(16cos2θ1-sin2θ1)t2+(16cosθ1-2msinθ1)t-(m2+12)=0.

設TA=t1,TB=t2,

設直線PQ的傾斜角為θ2,

TP=t3,TQ=t4,

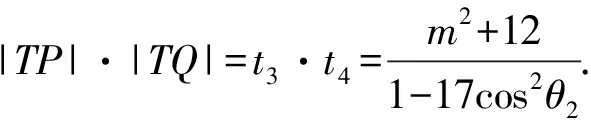
由|TA|·|TB|=|TP|·|TQ|,

得cos2θ1=cos2θ2.

因為θ1≠θ2,所以cosθ1=-cosθ2,

所以θ1+θ2=π,

所以tanθ1+tanθ2=0,

故直線AB的斜率與直線PQ的斜率之和為0.

解法三:點撥:利用圓冪定理

因為|TA|·|TB|=|TP|·|TQ|,

由圓冪定理知A,B,P,Q四點共圓.

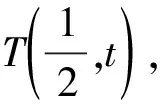
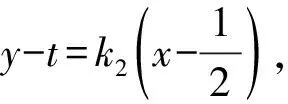
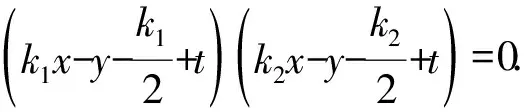
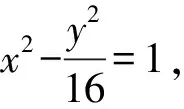
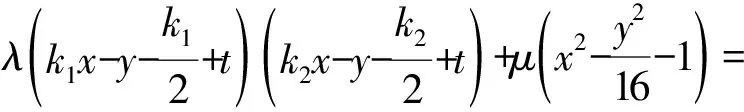
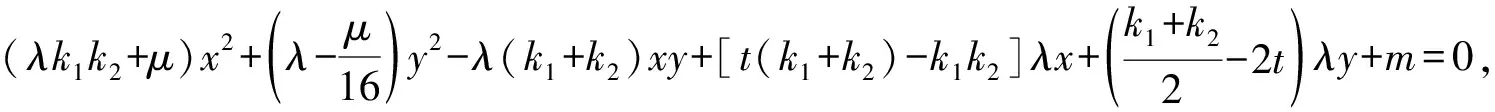
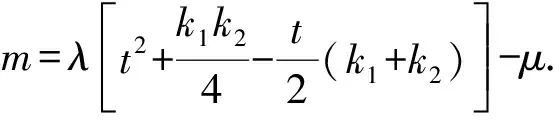
因為A,B,P,Q四點共圓,

所以xy項的系數為0,

即k1+k2=0.

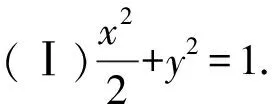
(Ⅱ)證明略.

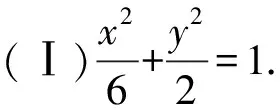
(作者單位 姓名：吉林省磐石市第二中學 韓兆峰)

【母題3】【解題策略】

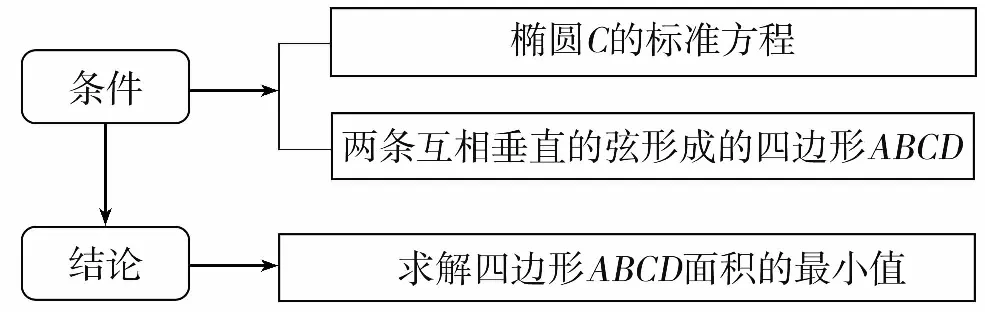
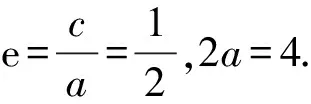
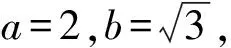
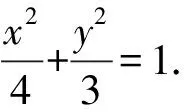
(Ⅱ)由題意知橢圓的右焦點F(1,0).

當兩條弦中一條弦所在直線的斜率為0,

另一條弦所在直線的斜率不存在時,

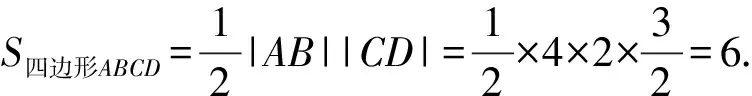
②當兩條弦所在直線的斜率均存在且不為0時,

設直線AB的方程為y=k(x-1),

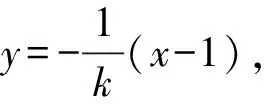
設A(x1,y1),B(x2,y2),

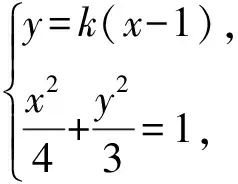
消y得(4k2+3)x2-8k2x+4k2-12=0,

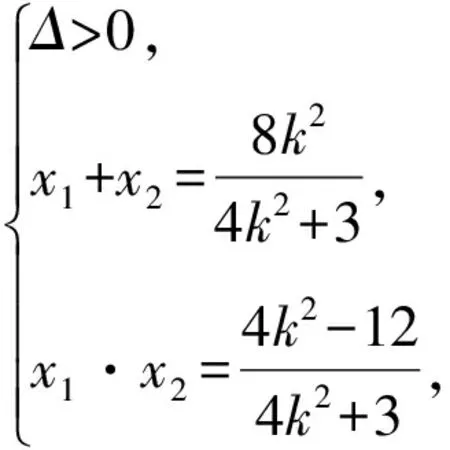
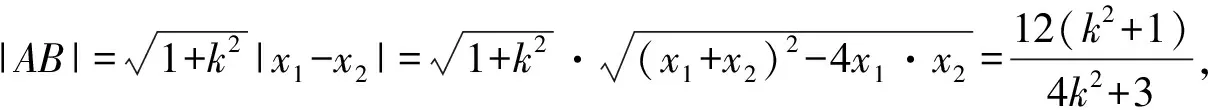
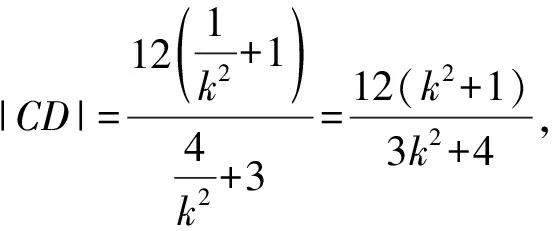
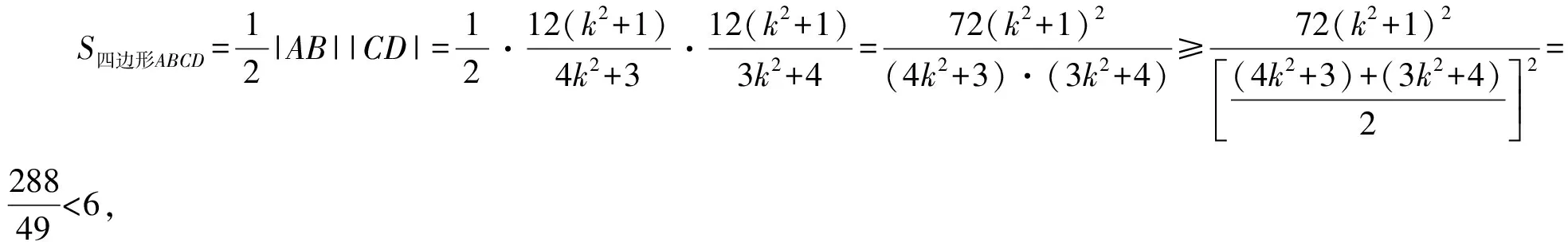
當且僅當4k2+3=3k2+4,

即k=±1時,等號成立.

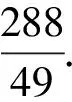
【方法總結】解決圓錐曲線中的取值范圍與最值問題的基本策略有:

幾何法:根據已知的幾何量之間的相互關系、平面幾何和解析幾何的相關知識加以解決(如拋物線上的點到某個定點和焦點的距離之和、光線反射問題等等).

代數法:題中的條件和結論能體現出明確的函數關系,則可先建立目標函數,再求這個函數的最值.

常從以下幾個方面考慮:

①利用判別式構造不等關系,從而確定參數的取值范圍;

②利用已知參數的范圍,求出新參數的范圍,解題的關鍵是建立兩個參數之間的等量關系;

③利用基本不等式求出參數的取值范圍;

④利用函數值域的求法,確定參數的取值范圍.

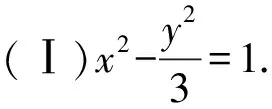
(Ⅱ)[6,+∞).

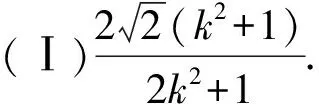
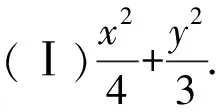
(Ⅱ)9.

(作者單位 姓名：河北省定州中學 趙偉娜)